基于多源数据融合的煤矿工作面瓦斯浓度预测*
2022-12-14董立红吴雪菲
谢 谦,董立红,吴雪菲,3
(1.中煤科工西安研究院(集团)有限公司,陕西 西安 710077;2.西安科技大学 计算机科学与技术学院,陕西 西安 710054;3.西安科技大学 能源学院,陕西 西安 710054)
0 引言
瓦斯灾害制约着高瓦斯矿井的安全生产[1-2]。预防和控制煤矿瓦斯灾害的发生成为当前煤矿安全生产亟需解决的问题。因此,瓦斯浓度预测技术成为煤矿安全生产领域的研究重点,有效的瓦斯浓度预测可为煤矿安全管理人员提供一定的参考依据。
目前,适用于瓦斯浓度的预测方法有传统方法和智能方法。传统方法围绕移动平均法进行瓦斯浓度预测,王鹏等[3]采用自回归差分移动平均(ARIMA)模型对煤矿井下瓦斯浓度进行预测;赵美成等[4]使用ARIMA和GARCH组合模型对煤矿井下瓦斯数据进行预测。智能方法以SVM,BP神经网络为主展开研究;钱建生等[5]利用粒子群算法优化支持向量机进行瓦斯浓度预测;李栋等[6]使用改进的混沌粒子群算法优化最小二乘支持向量机进行预测;郭思雯等[7]使用BP神经网络进行预测;刘弈君等[8]使用遗传算法优化BP神经网络进行预测。综上,均是在原有的基础上对算法的参数进行优化,并没有解决时序数据在时间上的关联关系。深度学习中循环神经网络(RNN)的出现有效解决了时序数据不能关联的缺陷[9]。李树刚等[10]采用RNN对瓦斯浓度进行了预测。但RNN存在“梯度消失”的问题。针对此问题,长短期记忆神经网络(LSTM)通过控制数据的流入问题,解决了RNN中由于tanh函数的控制出现在序列较长时候预测出现的“梯度消失”问题。因此,本文采用LSTM进行瓦斯浓度预测。
由于多数文献对瓦斯预测时候考虑的只有瓦斯浓度自身,并没有考虑周围环境对瓦斯浓度的影响,这并不能反映具体工作面空间中瓦斯浓度的真实情况,进而将对瓦斯浓度预测造成一定影响。本文将上隅角瓦斯浓度、采煤机速度、吨煤瓦斯涌出量、工作面风速、工作面CO浓度作为影响因素考虑进模型的输入。为了验证不同影响因素与瓦斯浓度的相关程度,使用互信息方法进行验证。为了突出各个影响因素在预测中关键作用,使用注意力机制(Attention Mechanism)为输入的影响因素分配权重,突出模型中更关键的影响因素[11]。因此,本文提出1种基于多源数据融合的工作面瓦斯浓度预测模型。
1 Attention-aLSTM模型
1.1 模型输入层
当前使用数据的采集传输大多通过网络,而网络传输受外界因素、传输速度等影响,易出现较小范围内的尖峰与谷底数据,尖峰数据与谷底数据会大幅度影响预测的精度,因此在预测前需要对采集的数据进行尖峰与谷地数据的处理,即异常值处理,处理步骤如下:
1)使用拉伊达准则[12]进行异常值确定,并将异常值置为NULL或0;
2)使用Lagrange插值法[13]对NULL或0位置的数据进行插值,使其前后数据连接平滑。
由于LSTM网络中sigmoid的特性,对[-1,1]内的数据敏感,因此对输入数据进行归一化处理。如式(1)所示:
(1)
式中:x′为归一化变量;x为样本数据;max(x)和min(x)分别为模型输入的最大值和最小值。
工作面瓦斯浓度易受工作面CO浓度、工作面风速、上隅角瓦斯浓度、采煤机速度、吨煤瓦斯涌出量等因素影响。为了提高工作面瓦斯浓度的预测精度,将同时刻内的相关数据进行整合,如图1所示,进而形成1个新的时间序列。
为了验证新数据中t时刻的工作面瓦斯浓度数据和其他时刻数据是否存在相关性,使用互信息进行相关性验证,互信息公式如式(2)所示:
(2)
式中:p(x,y)是工作面瓦斯浓度与某一影响因素的联合概率密度函数;p(x)和p(y)分别是是工作面瓦斯浓度和某一影响因素的边际概率密度函数。
使用互信息(Mutual Information, MI)值对比工作面瓦斯浓度数据与上述影响因素之间的相关程度,计算结果如表1所示。

表1 互信息计算结果Table 1 Mutual information calculation results
由表1可知,工作面CO浓度、上隅角瓦斯浓度、吨煤瓦斯涌出量、采煤机速度4种影响因素为主要影响因素,可做为模型的输入。
1.2 LSTM网络层
RNN使用较长序列进行预测时会出现“梯度消失”的问题[14]。LSTM使用存储单元来存储和输出信息,解决了RNN存在的缺陷[15-16]。如图2所示,为LSTM单元结构。
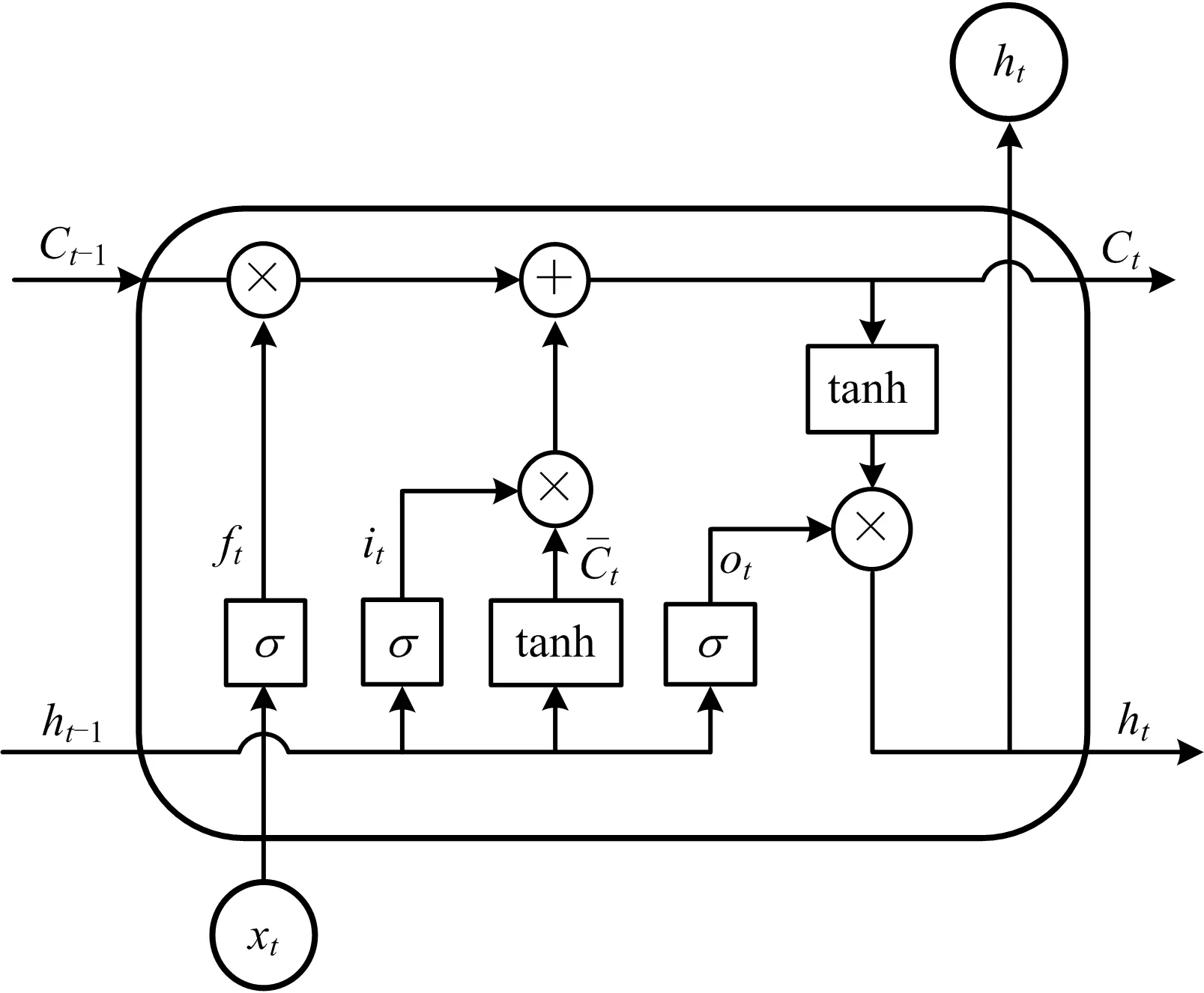
图2 LSTM单元结构Fig.2 LSTM cell structure
LSTM的细胞单元具有3个门,分别为遗忘门(Forget Gate)、输入门(Input Gate)、输出门(Output Gate)[17]。σ表示sigmoid激活函数,将处理后的数据输入至LSTM细胞单元参数更新步骤如式(3)~(8)所示:
ft=σ(Wf·[ht-1,xt]+bf)
(3)
it=σ(Wi·[ht-1,xt]+bi)
(4)
(5)
(6)
ot=σ(Wo·[ht-1,xt]+bo)
(7)
ht=ot·tanh(Ct)
(8)
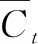
1.3 Attention机制层
Attention机制将LSTM模型的输出作为Attention机制层的输入特征,计算各输入特征权重,根据权重突出输入特征中的关键特征,降低对非关键特征的关注,帮助模型做出更加精准的特征选择[18-19]。Attention结构如图3所示。
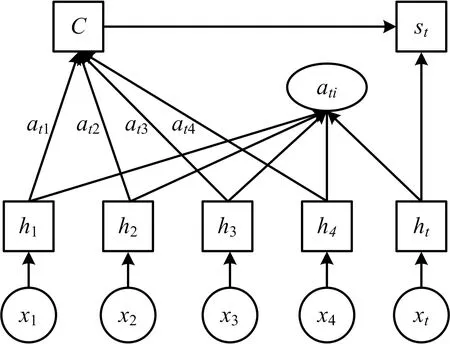
图3 Attention单元结构Fig.3 Attention cell structure
图3中,x1,x2,…,xt表示多源融合数据的输入;h1,h2,…,ht表示输入对应的LSTM隐藏层输出的状态值;ati表示LSTM隐藏层输出值对应当前的注意力权重值;st表示Attention机制层输出的状态值。
具体计算步骤如式(9)~(12)所示:
et,i=VT·tanh(Wht+Uhi),i=1,2,…,t-1
(9)
(10)
(11)
st=f(C,ht)
(12)
式中:et,i为h1,h2,…,ht-1分别与ht的相关性;at,i为各et,i占总体的概率;C为注意力权重;V,W,U为训练参数,随迭代不断进行调整。
1.4 Adam优化算法
Adam优化算法融合了AdaGrad算法和RMSProp算法的优点[20],该算法基于低阶矩阵的自适应估计,其中模型梯度的一阶矩估计和二阶矩估计计算公式如式(13)~(14)所示:
mt=β1mt-1+(1-β1)gt
(13)
(14)
式中:mt为梯度的一阶矩估计;vt为梯度的二阶矩估计;β1,β2为系数(β1=0.9,β2=0.999);gt为梯度值。
由于在初始化时赋予mt和vt初始向量值为0,衰减率将偏向零向量,因此需对mt和vt进行偏差校正。一阶矩估计偏差校正和二阶矩估计偏差校正公式如式(15)~(16)所示:
(15)
(16)
经过偏差校正后的Adam算法公式如式(17)所示:
(17)
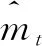
1.5 Attention-aLSTM模型
预测步骤如下:
1)将多源融合数据作为模型的输入,根据LSTM对输入格式的要求,将输入量转换为样本数×步长×特征数,即N×1×4;
2)将转换后适应LSTM网络的数据分为训练集、测试集,并进行归一化;
3)将归一化后的训练数据输入至LSTM网络层,训练后将隐藏层的输出输入至Attention机制层,最终得到赋权后的状态值;
4)将Attention机制层的输出通过全连接层得到该次训练下的预测结果;
5)使用Adam作为Attention-aLSTM模型的优化器,通过迭代训练该数据集下最优的Attention-aLSTM预测模型;
6)将测试集数据输入至训练好的Attention-aLSTM模型中,获取未来时刻范围内的预测结果。
Attention-aLSTM模型如图4所示。
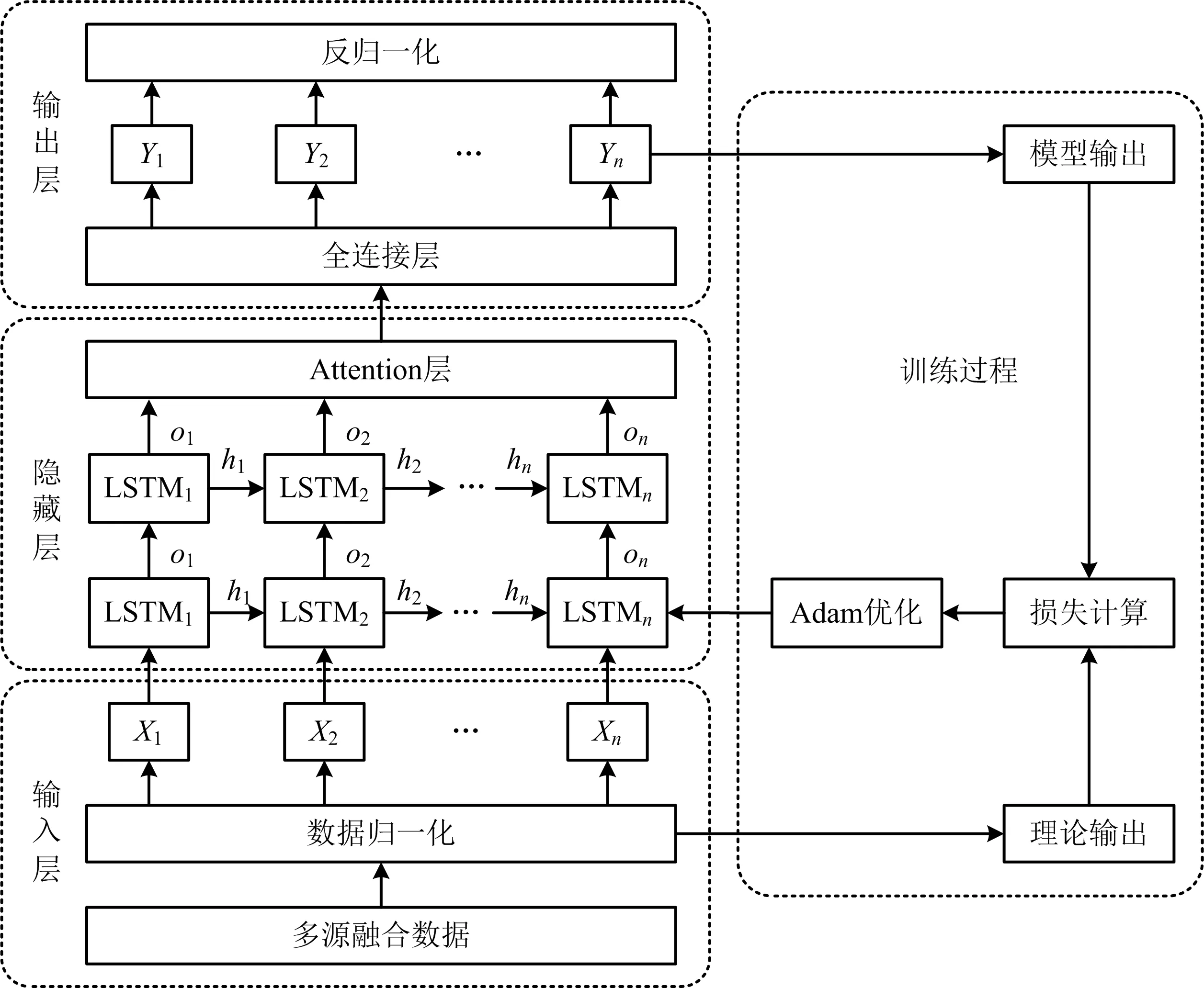
图4 Attention-aLSTM预测模型Fig.4 Attention-aLSTM prediction model
2 实例分析
2.1 实验工具及数据集
本文采用深度学习中的Keras库搭建LSTM模型。使用Python中modbus_tk库通过TCP/IP通信协议读取某矿1008工作面的实时数据并存入MySQL数据库中。
本文采用考虑影响因素和不考虑影响因素2种形式进行实验。共采用5 000条数据,选取前4 880条数据作训练集,后120条数据作测试集。
2.2 参数设置
首先,采用Relu来提高运行深度并减少梯度下降;其次,对比不同层数下的预测效果,确定隐藏层层数;再次,选取合适的隐藏层节点个数,确定学习率;最终确定合适的步长。最后,得到LSTM模型的参数:节点数32,层数2,学习率0.001,优化器Adam。
为了有效对比预测效果,本文使用支持向量机(SVM)、BP神经网络、LSTM神经网络与Attention-aLSTM神经网络进行对比,其中Attention-aLSTM神经网络LSTM层参数与LSTM神经网络参数选取保持一致,参数设置如表2所示。
2.3 评价指标
评价指标采用平均绝对百分比误差(MAPE)和均方根误差(RMSE),如式(18)~(19)所示:
(18)
(19)
式中:Ytrue,i为待预测真实对比值;Ypre,i为模型预测值。
2.4 瓦斯浓度预测结果分析
为对比预测效果,将验证实验分为输入模型考虑影响因素和不考虑影响因素2种。
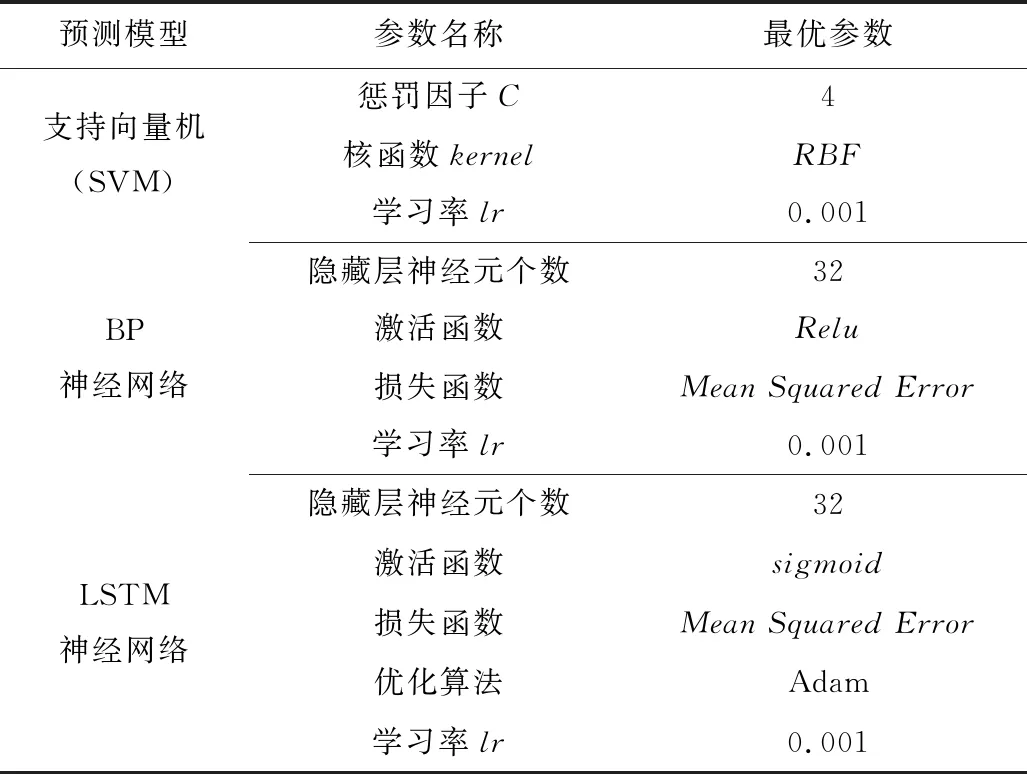
表2 对比模型参数设置Table 2 Parameters setting of comparative models
不考虑影响因素下各模型的效果对比如图5所示。
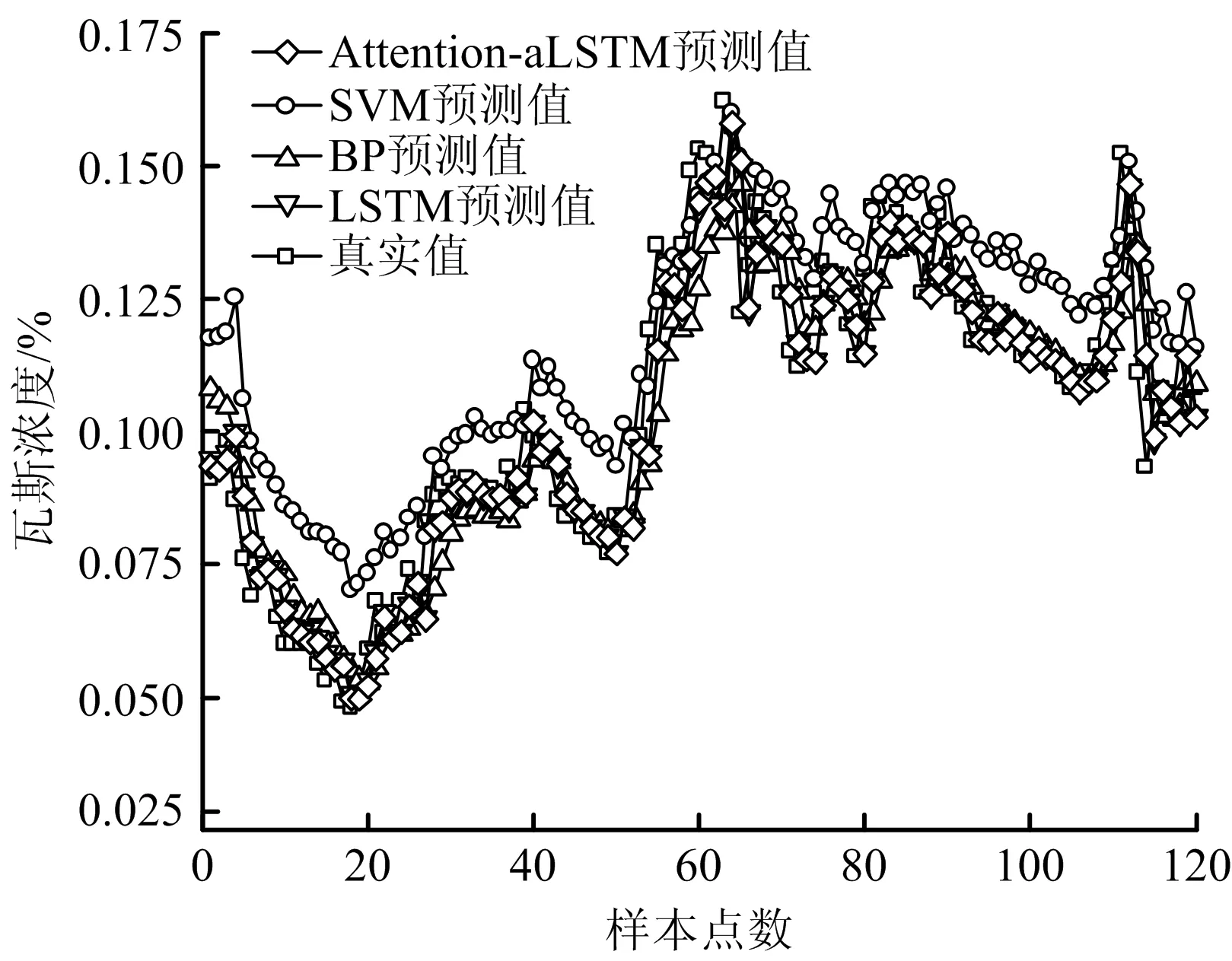
图5 不考虑影响因素下真实与预测结果对比Fig.5 Comparison of real and predicted results without considering influence factors
由图5可知,Attention-aLSTM的整体预测结果优于其他模型的预测效果。预测误差对比如表3所示。
由表3可知,Attention-aLSTM在测试集上的测试精度优于其他模型的预测精度,单变量下的Attention-aLSTM预测效果相比LSTM提升了14.2%。
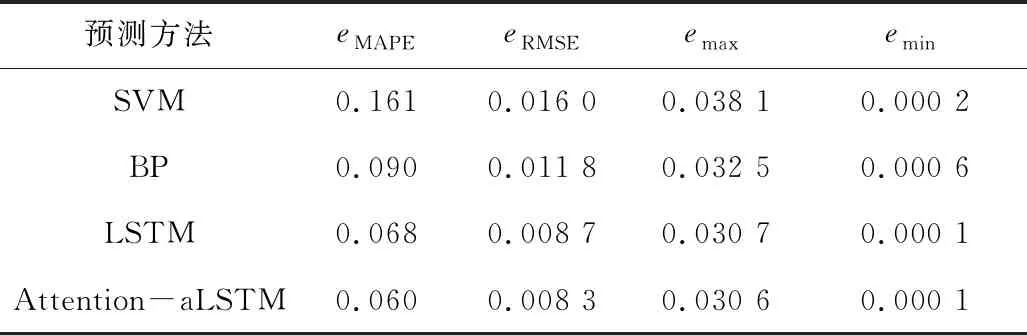
表3 预测误差对比Table 3 Prediction error comparison
考虑和不考虑影响因素下Attention-aLSTM预测与真实值如表4和图6所示。

表4 考虑和不考虑影响因素预测误差对比Table 4 Comparison of prediction errors considering and not considering influencing factors
由图6可知,考虑影响因素条件下的预测精度较好。
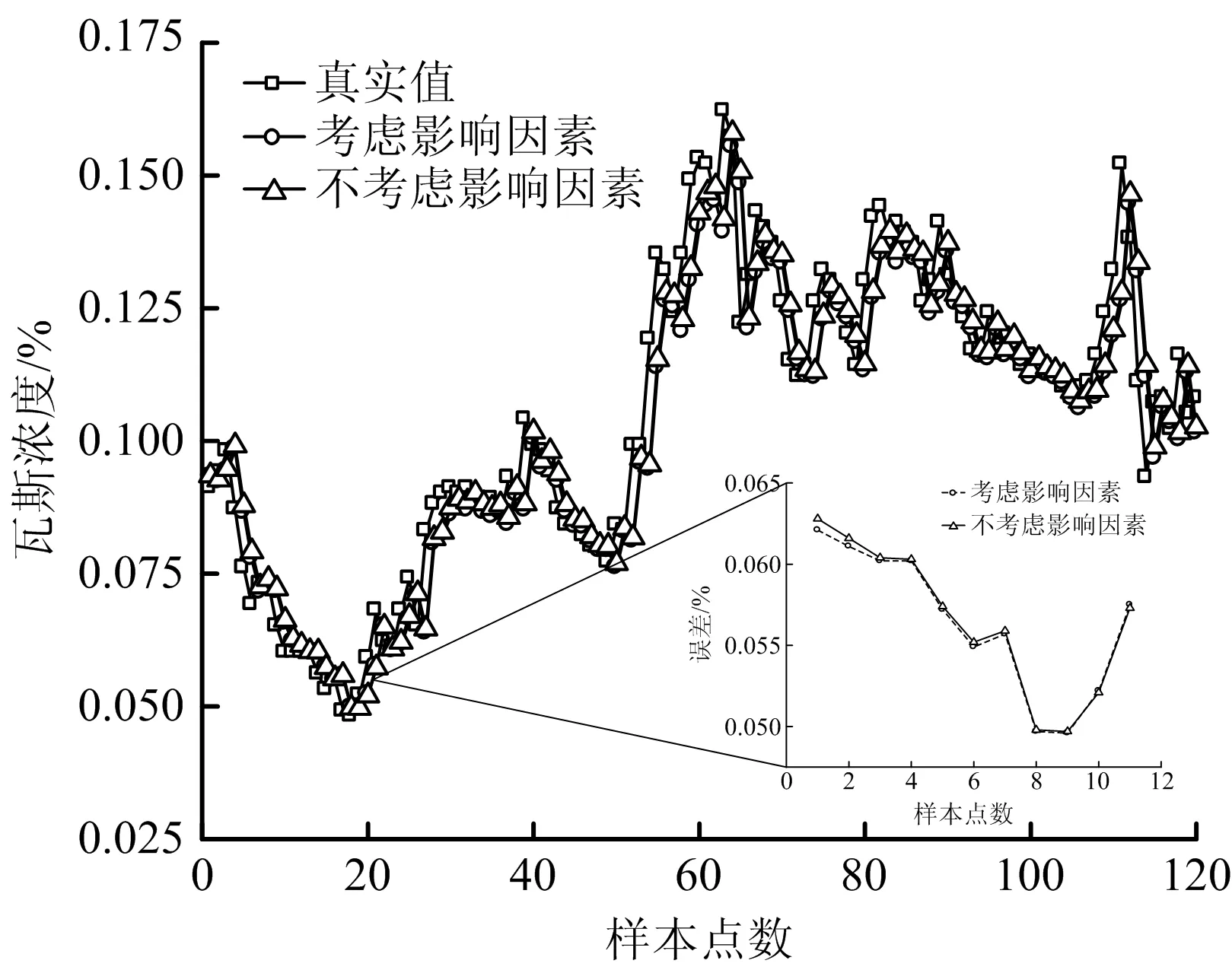
图6 考虑和不考虑影响因素下真实与预测结果对比Fig.6 Comparison of real predicted results considering and not considering influencing factors
3 结论
1)将多源数据作为预测模型的输入比单一使用瓦斯浓度进行预测的精度要高。
2)注意力机制突出影响因素中的关键信息,将其引入LSTM网络中,提升瓦斯浓度的预测精度。
3)LSTM预测模型具有时序性特征,当前时刻的输入与上一时刻的输入有关,可以针对瓦斯浓度时序性数据的特性进行预测。经过实验验证,LSTM可以有效地预测下一时刻瓦斯浓度,可为煤矿安全生产管理提供一定的参考意见。
