基于路网协同维护的灾后配电网抢修优化研究*
2022-12-14马传奇王国庆朱建明
马传奇,王国庆,于 雷,朱建明,黄 钧
(1.中国科学院大学 工程科学学院,北京 100049;2.齐齐哈尔北车辆段,黑龙江 齐齐哈尔 161099;3.中国科学院大学 应急管理科学与工程学院,北京 100049)
0 引言
当今社会,电网成为人们赖以生存的基础生命线设施[1-2],极端灾害造成的停电事件往往带来巨大损失。近年来极端灾害频发,我国南方在2008年发生罕见冰雪灾害,造成约170个县市的大范围停电事故,直接损失超过百亿[3];2017年美国遭遇Harvey飓风与Iram飓风,大量的配电网设施被损坏,导致约1 500万用户的停电[4]。因此,配电网的灾后应急抢修工作具有重要研究价值。
极端灾害不仅损坏配电网,也会对路网造成破坏。以往研究大多忽略路网损坏状况,因配电网规模较小而忽略抢修途中的行驶时间[5]。但现实中,路网损坏常使配电网的应急抢修难以展开,如2021年7月的河南洪灾中,道路中的洪水严重阻碍配电网的抢修工作[6]。因此,在配电网的灾后抢修中,路网损坏状况不能忽略,路网维护十分必要。
目前配电网的抢修研究中,常以最小化减负荷为目标,通过应急抢修与拓扑重构实现配电网的运行恢复。文献[7]基于配电网的灾后重构提出受损线路的复电路径概念,研究多配电抢修队协作抢修下的配电网快速复电问题;文献[8]在最小化减负荷的目标下,利用SNOP在配电网故障期间维持不间断供电和提高电能质量的灵活控制特性;文献[9]针对灾后非故障区域的负荷断电状况,在抢修过程中对开关刀闸进行重构,通过改变负荷的供电路径使失电负荷尽可能恢复供电。
微电网在近些年成为配电网的灾后研究热点,其原理为孤岛运行下,通过利用风能或太阳能等分布式电源维持微电网运行[10]。文献[11]基于配电网的径向分布,通过形成多个由分布式电源供电的微电网,以实现灾后对关键负荷的供电;文献[12]提出使用内燃机车辆作为微电网的能源,以在灾后增强系统的灵活性;文献[13]考虑到微电网内发电资源的可变性和稀缺性提出三级供电恢复方法,通过应急发电车和微电网来协同恢复所有关键负荷,并抢修各时期的非关键负荷来实现配电网的灾后恢复。
文献[14]建立的配电网弹性恢复物流中将灾后道路分为可行和不可行,并进行配电抢修队与分布式发电机的协作调度;文献[15]建立加权动态分配模型用以刻画路网实时状态,对移动应急电源与配电抢修队进行协同调度。然而,上述文献在配电网的灾后抢修中均没有考虑路网维修的协同。因此,本文展开路网维护协同下配电网的灾后调度抢修研究,并探索路网维护如何影响配电网的调度维修,以期找到路网维护与配电网维修之间的影响机制,为现实背景下灾后配电网维修与路网维护的协同优化工作提供参考和借鉴。
1 问题描述与模型假设
极端灾害发生期间,随断电用户数量不断增加,配电网性能不断降低;灾害结束时,性能降至最低;灾害结束后,配电网的抢修工作展开,随着损坏线路的不断维修直至配电网完全恢复。极端灾害发生后配电网的系统性能变化趋势如图1所示。

图1 系统性能变化曲线Fig.1 Curve of system performance change
图1中,R(t)为系统性能水平随时间变化的度量;t0,t1分别表示极端灾害发生时刻和配电网受损的开始时刻;t1~t2期间,随断电用户数量增加,系统性能逐渐降低,直至灾害结束的t2时刻下降至性能最低点Rmin;在t3时刻开始抢修配电网;至t4时刻,配电网完全恢复,此时断电用户都重新连接到公用电网;t4时刻之后,系统性能恢复到正常水平。
电网研究中常采用如图2(a)所示的配电网接线图,表示配电网的灾后损坏状况,其中损坏线路有0-1,3-4,4-5,其余为线路完好。本文将重构后依然连接在一起的失电负荷视为1个超级节点,表现为同时断电、通电,可转换为图2(b)接线图G′,表示超级节点的复电顺序。图2(b)中N1={1,2}表示由失电负荷1和2构成的超级节点,类似有N2={4,6},N3={5}。应急仓库及配电故障点(即超级节点)的位置可在地图中获得,路网状况图可通过无人机获得。将应急仓库和超级节点的位置耦合到路网中,形成如图3所示的耦合路网状况图,其中2点间的道路有且仅有可行与损坏2种状态。
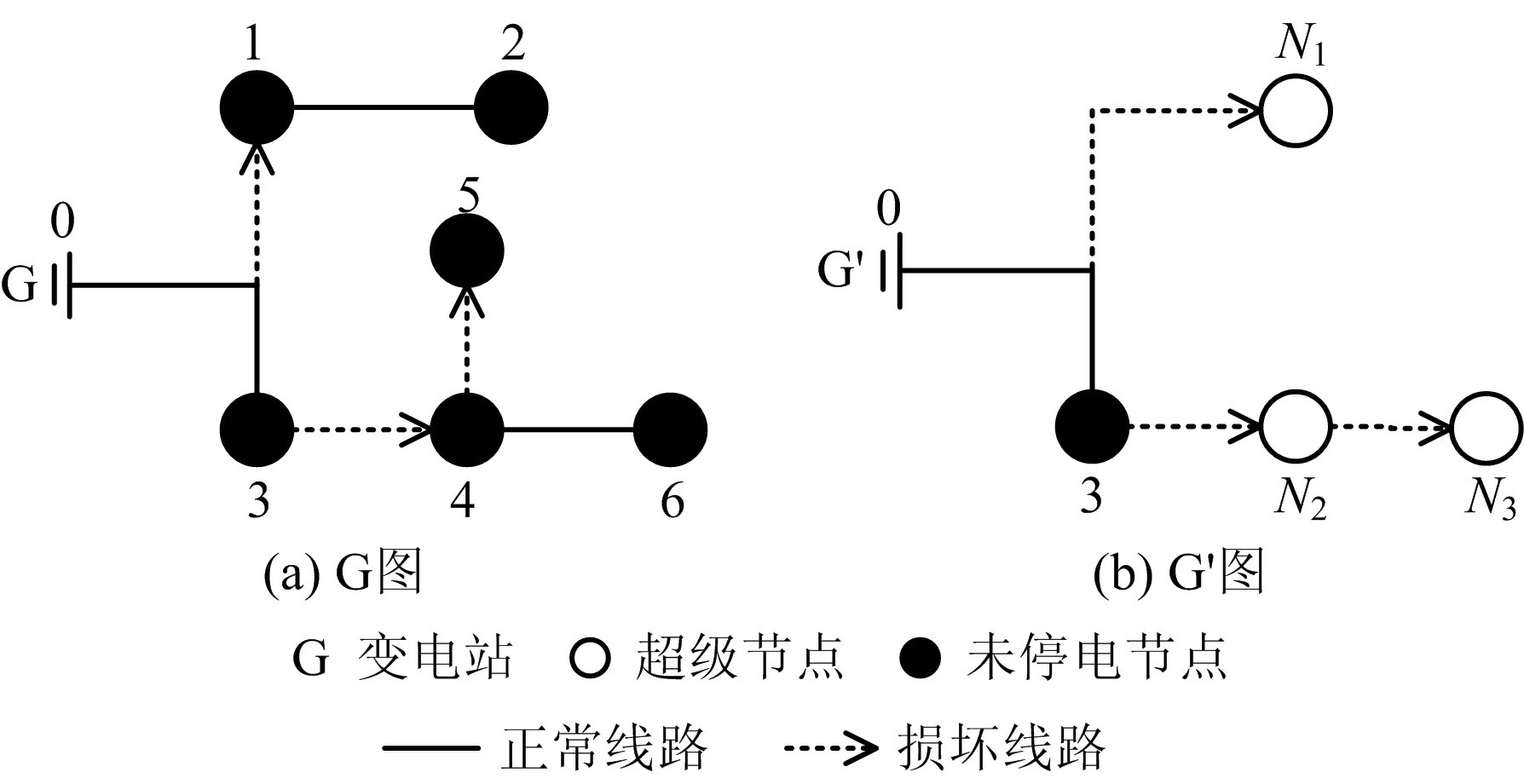
图2 配电网接线图G,G′Fig.2 Wiring diagram of power distribution network G,G′
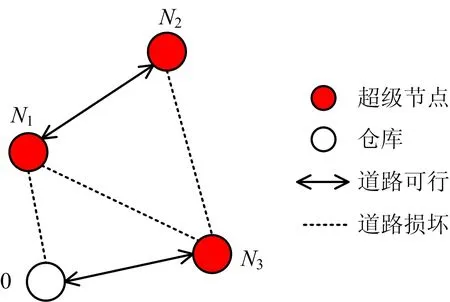
图3 耦合路网状况Fig.3 State of coupled road network
如果不考虑路网损坏,相较于损坏电路的维修时间,配电网抢修队的行驶时间可忽略不计。假设本例仅有1支配电抢修队,各超级节点的维修时间和权重都为1,P1,P2,P3分别表示超级节点N1,N2,N3的有功需求且分别为3,2,1。如果不考虑路网损坏状况,此时基于P1>P2>P3与复电路径,优化后的维修顺序为N1-N2-N3;如果考虑路网损坏且耦合路网状况如图3,假设仅有1支路网维护队,每条损坏道路的维护时间都为Tl,则此时基于P1>P2>P3、复电路径以及损坏路网通行状况,有Tl≤0.5时,配电网的最优抢修顺序为N1-N2-N3,否则为N3-N1-N2。因此,配电网的调度维修中,损坏路网状况不可忽略。
基于此,本文构建的模型包含路网抢修策略约束、配电网维修策略约束及配电网运行约束。假设灾害发生后,配电网与路网的损坏状况可以立即获得;由于大约90%的灾后配电网受损情景是线路损坏,因此假设配电网的损坏情景都为线路损坏;由于配电网规模小,假设可行道路的所需行驶时间可忽略不计[5],损坏道路在被修好前不可行。
2 考虑损坏路网维修的灾后配电网恢复策略模型
2.1 模型中的集合、参数、变量定义
模型的集合与标记、参数、变量的定义如表1~3所示。

表1 集合和标记Table 1 Sets and labels

表2 参数Table 2 Parameters

表3 变量Table 3 Variables
2.2 数学模型
2.2.1 目标函数
灾害发生后,如医院等重要用户应被优先考虑恢复供电。配电网中,各节点通过消耗有功功率而工作,无功功率不被消耗。因此,假设配电网完全恢复至多花费的时间为T,则目标函数f为最小化加权减负荷,如式(1)所示:
(1)
2.2.2 路网抢修策略约束
路网抢修策略约束条件如式(2)~(11)所示。其中,式(2)表示路网维护队在任意时刻至多维护1条损坏道路;式(3)表示任意损坏道路在维护时间不小于其所需要时间时才可行;式(4)表示任意损坏道路开始维护后的状态,要么在维护中,要么被维护好;式(5)表示任意损坏道路最多被维修1次;式(6)表示任意道路的可行时刻在其被维护好之后;式(7)表示任意损坏道路一旦维护好就一直可行;式(8)表示非损坏道路一直可行;式(9)表示任意损坏道路被维护好之后才可行;式(10)表示任意损坏道路的维护调度开始时其处于被维护中;式(11)表示任意损坏道路一旦可行后就一直可行。
(2)
(3)
(4)
(5)
(6)
vmn,t≤vmn,t+1,∀(m,n)∈Ed,t∈(1,T-1)
(7)
emn,t=1,∀(m,n)∈EEd,t
(8)
emn,t≤vmn,t,∀(m,n)∈Ed,t
(9)
γmn,t≤αmn,t,∀(m,n)∈E,t
(10)
emn,t≤emn,t+1,∀(m,n)∈Ed,t∈(1,T-1)
(11)
2.2.3 配电网维修策略约束
配电网维修策略约束条件如式(12)~(22)所示。其中,式(12)表示每个配电抢修队在任意时刻仅维修1个超级节点;式(13)表示任意超级节点被维修的总时长不小于其所需时间才被修好;式(14)表示每个超级节点开始被维修后要么在维修中,要么被维修好;式(15)表示每个超级节点仅被维修1次;式(16)表示任意超级节点是否开始维修受其与上一维修点间的道路状况限制;式(17)表示在配网拓扑上任意超级节点与前一节点的连通时刻在其被修好的时刻之后;式(18)表示任意超级节点一旦被修好就一直保持修好状态;式(19)表示任意超级节点仅被修好后才能通电;式(20)表示任意超级节点的复电路径约束,任意超级节点仅在其复电路径集合均处于通电状态后才能通电;式(21)表示任意超级节点的维修调度开始时其处于被维修中;式(22)表示任意超级节点一旦通电就一直保持通电状态。
(12)
(13)
(14)
(15)
(16)
(17)
zm,t≤zm,t+1,∀m∈Bd,t∈(1,T-1)
(18)
ym,t≤zm,t,∀m∈Bd,t
(19)
ym,t≤yh,t,∀m∈Bd,h∈Em,t
(20)
bm,t≤λm,t,∀m∈Bd,t
(21)
ym,t≤ym,t+1,∀m∈Bd,t∈(1,T-1)
(22)
2.2.4 配电网运行约束
配电网运行约束条件如式(23)~(32)所示。其中,式(23)~(26)分别表示变电站的有功功率,无功功率平衡;式(27)表示变电站的发电功率约束;式(28)表示配网节点的功率约束;式(29)表示损坏线路的视在功率约束;式(30)表示任意节点处的电压约束;式(31)表示任意损坏线路的LinDistFlow潮流模型[16];式(32)表示功率非负约束。
(23)
(24)
(25)
(26)
(27)
0≤Pi,t≤Pi,0≤Qi,t≤Qi,∀i∈Vd,t
(28)
(pfij,t)2+(qfij,t)2≤ym,t(Sij,max)2,∀lm=(i,j),t
(29)
(Vmin)2≤(Vi,t)2≤(Vmax)2,∀i∈Vd,t
(30)
(31)
pfij,t≥0,qfij,t≥0,∀i,j∈Vd,t
(32)
3 求解算法
本文采用Jacques F.Benders在1962年提出的Benders分解算法,其是1种用于解决混合整数规划问题的常用算法。本文将其应用于求解路网—配电网协同抢修模型,并将所提的模型分解为主问题和子问题。
3.1 模型线性化

(33)
bmtn≤zn,t,bmtn≤emn,t,zn,t+emn,t-1≤bmtn
(34)
式(30)~(31)中的非线性是由于二次项造成的,可用ρi,t表示(Vi,t)2来消除二次项;式(29)中的二次项可以采用文献[17]中的消二次项法,则式(29)可由式(35)表示:
(35)
3.2 子问题
(36)
s.t.式(23)~(28),式(30)~(32),式(35).
将上述问题转化为对偶子问题(DSP)如式(37)~(46)所示:
(37)
(38)
(39)
(40)
(41)
(42)
(43)
(44)
(45)
(46)
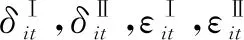
3.3 主问题
对应的主问题(MP)如式(47)~(48)所示:

(47)
(48)
3.4 算法步骤
1)初始化上界UB=+∞,下界LB=-∞。
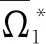
4)如果UB-LB≤Gap,迭代停止,否则构造1个形如式(48)的最优割平面(benders optimality cut)到主问题模型中,并转向步骤2),直到算法结束。
4 算法仿真
本文参照云南鲁甸某地10 kV配电网构造的辐射型配电网案例,配电网简化接线图如图4所示。图4中有变电站1个,电力用户24个以及分支节点4个。各电力用户的权重相同且为1。变电站的最大输出功率为6.6 MW,各用户节点的功率需求按照其电气接线图变压器的装接容量计算。采用的电线均为LJG-50,参数设定为0.58 Ω/km,线路电阻按照实际距离计算。假设配电抢修队有2支,1支和2支配电抢修队抢修1条损坏线路的时间分别为7 h和4 h;路网维护队有1支,每条损坏道路的维护时间相同且随机选取[1,10]之间的整数,单位为h。
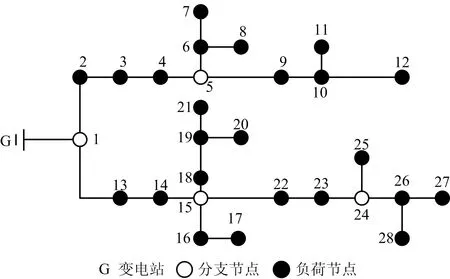
图4 鲁甸某地电网简化接线图Fig.4 Simplified wiring diagram of power distribution network in a region of Ludian
假设灾后损坏的7条配电线路为1-2,4-5,10-11,13-14,18-19,15-16,24-26,配电网重构后形成超级节点N1~N7,对应的功率需求如表4所示,复电路径如图5所示。将应急仓库和超级节点的位置耦合到路网中,形成如图6所示的灾后耦合路网状况图。

表4 超级节点的有功及无功功率需求Table 4 Active power and reactive power required by super nodes

图5 超级节点复电路径Fig.5 Power recovery path of super nodes
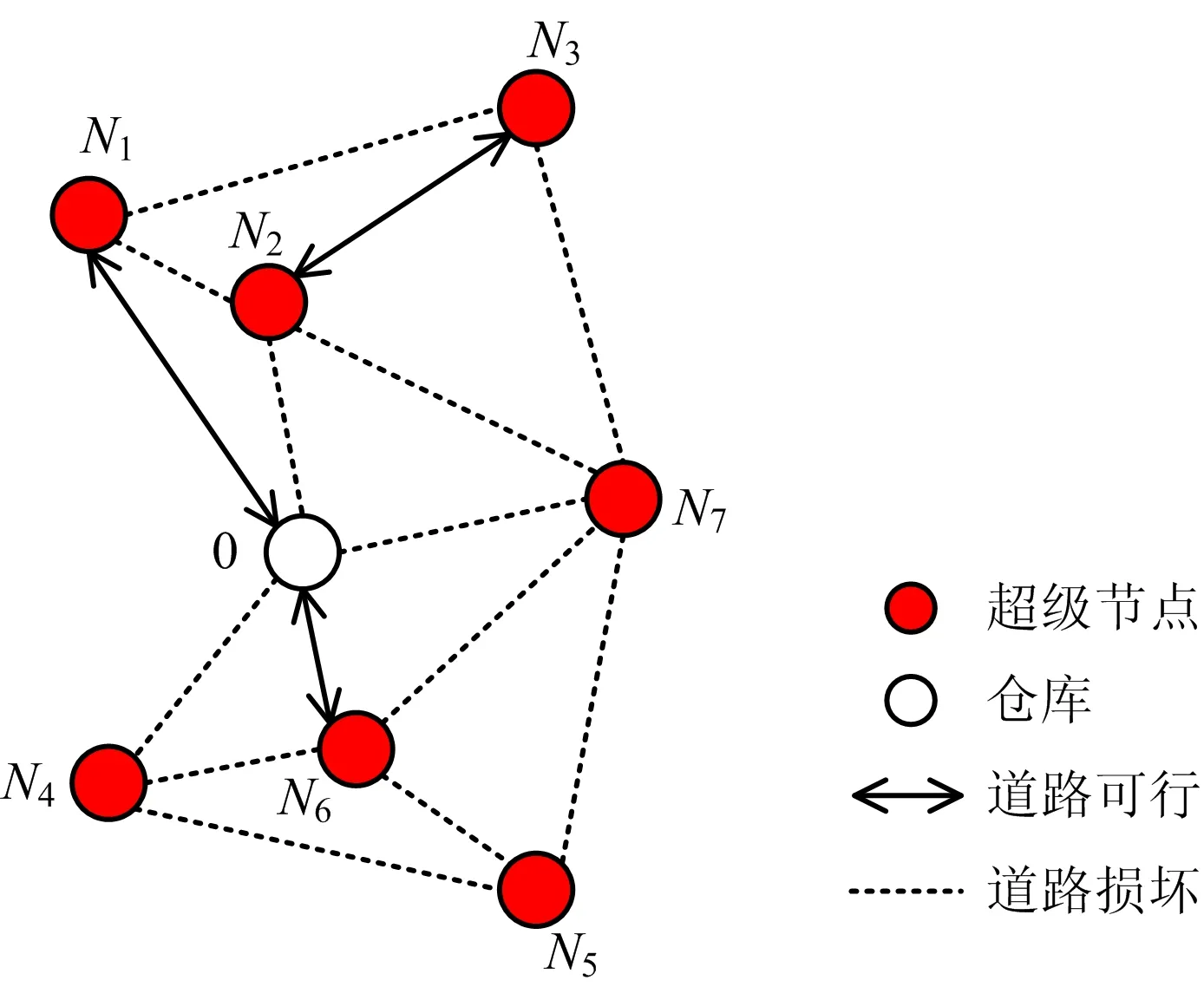
图6 灾后耦合路网状况Fig.6 State of post-disaster coupled road network
假设每条损坏道路的维护时间相同并依次选取[1,10]内的整数,可得如表5所示的最优抢修顺序安排和如图7所示的配电网恢复时间的趋势。
如果不考虑路网损坏,配电网的最优抢修顺序为13-14,1-2,4-5,10-11,24-26,15-16,18-19,恢复时间为28 h。由表5和图7可知,如果考虑道路损坏,最优抢修顺序发生改变,说明道路损坏状况不能忽略。且结合表5和图7可以得到:1)道路维护时间为4 h是转折点;2)道路维护时间在4 h及以内,配电网的最优抢修顺序相同,在4~7 h最优顺序不断改变,在7~10 h最优顺序相同;3)道路维护时间在4 h及以内时,配电网的恢复时间相同,在4~10 h恢复时间逐渐延长。
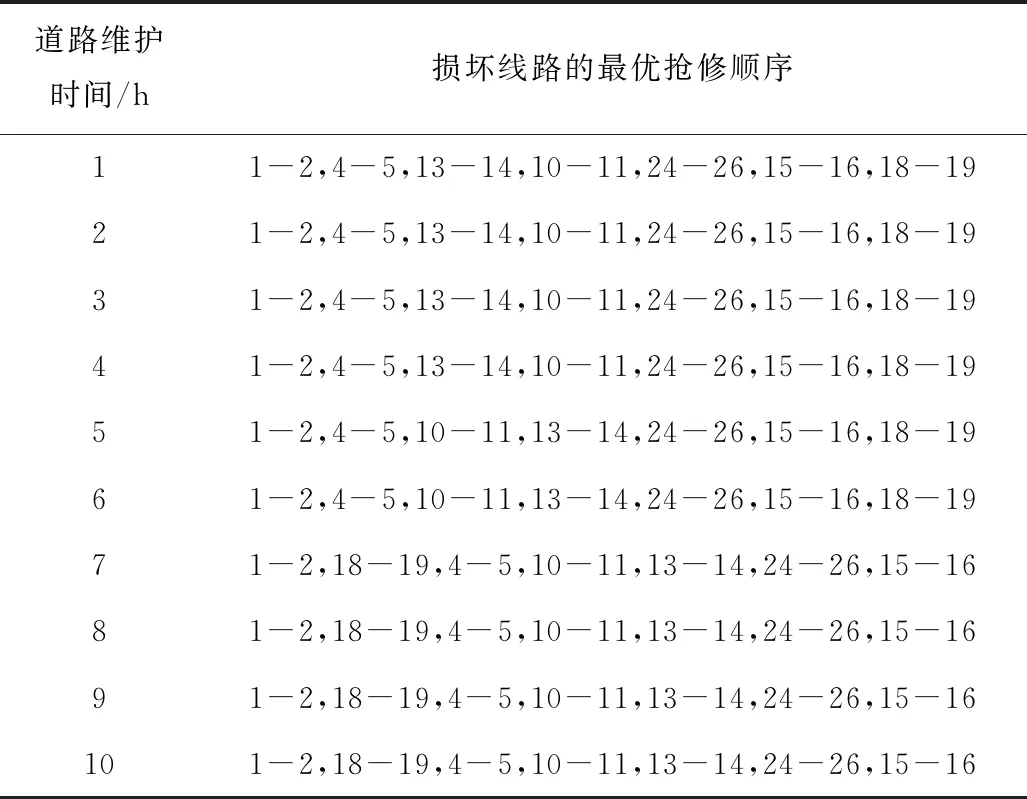
表5 配电网的最优抢修顺序安排Table 5 Optimal rush-repair sequence arrangement of power distribution network
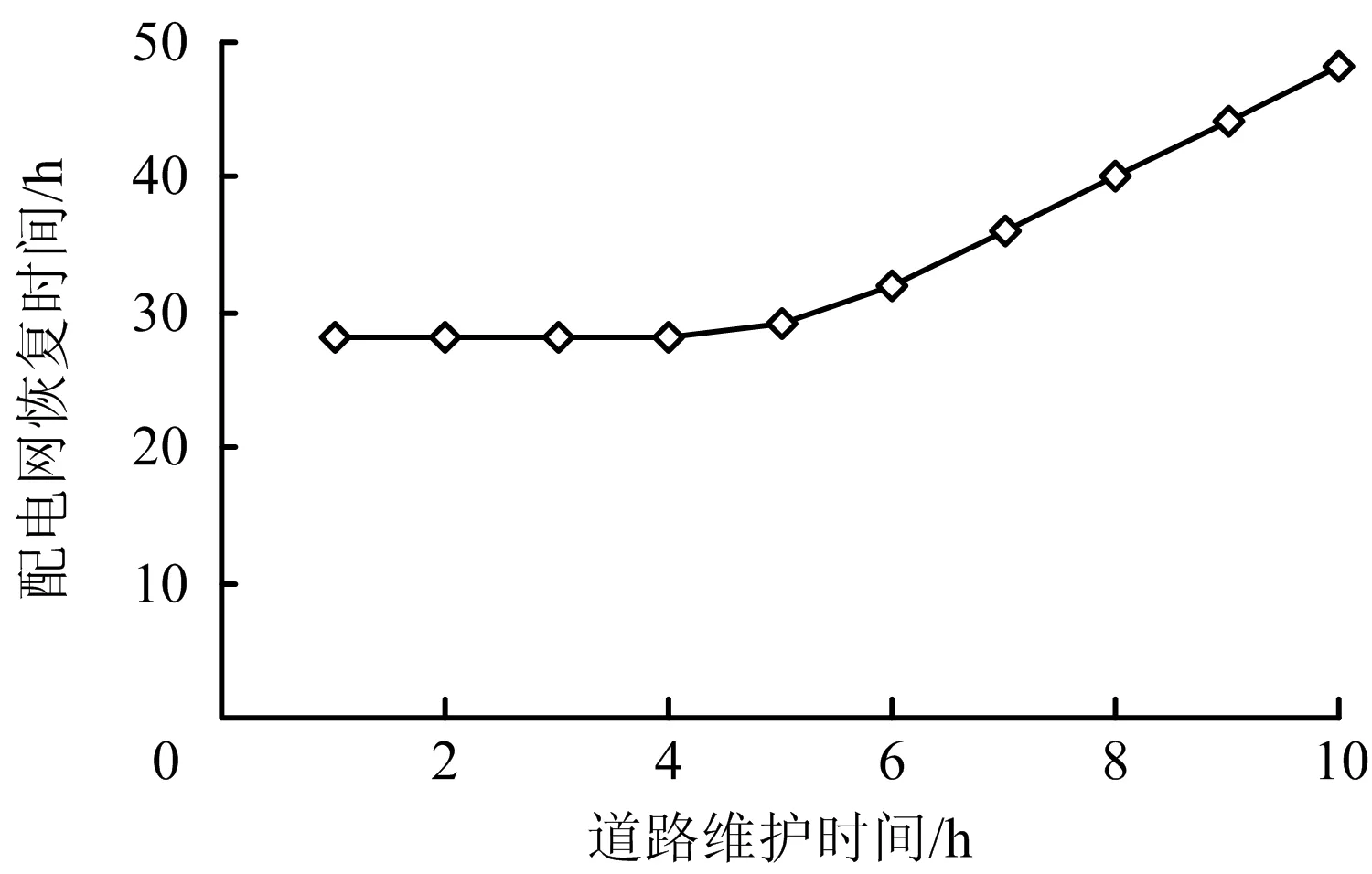
图7 不同道路维护时间下的配电网恢复时间变化Fig.7 Change in recovery time of power distribution network under different maintenance time of road
本文将案例中的7步配电网抢修顺序安排称作7步时序安排,将考虑和不考虑路网损坏时的时序安排进行对照求出重合数,定义时序变异数=7-重合数,如表5中,当道路维护时间为4 h时,时序变异数为3。为避免上述案例结果的偶然性,其他条件不变下,假设每条损坏道路的维护时间都为4 h,各超级节点的权重可在{0.5,1}中随机选取,可得128个案例构成的案例组,并定义每个案例的权重变异数为该案例中超级节点权重取值0.5的数量。运行后可得时序变异数随权重变异数变化的分布情况如图8所示,其中点(0,3,1)表示当所有超级节点的权重都为1时,与不考虑道路损坏相比,考虑道路损坏时的配电网维修时序变化数为3,且案例组中,时序变异数大于3的占据74.2%。因此进一步说明配电网的灾后抢修中,路网维护的协同是必要的。

图8 权重变化下时序变异数分布Fig.8 Distribution of time series variance under changed weight
5 结论
1)道路损坏会阻碍灾后配电网的维修调度工作,因此在配电网维修期间,路网维护必不可少。
2)本文构建路网-配电网协同抢修模型,模型采用Benders求解算法,通过不断生成最优平面以求得最优解,并通过案例验证模型的有效性。
3)案例表明配电网的灾后维修调度中,考虑路网的协同维护是必要的。配电网的恢复时间受到损坏路网的维护力量影响,随着路网的维护力量提高,配电网的恢复时间先逐渐减小后趋于不变,因此,路网维护队与配电抢修队的力量配比很重要。当配电抢修队的力量一定,如果路网维护队的力量跟不上,配电网的恢复时间会被动延长;反之,路网维护队的力量得不到充分利用。
