Soil texture affects the conversion factor of electrical conductivity from 1:5 soil-water to saturated paste extracts

Bo-Seong SEOYoung-Jae JEONGNu-Ri BAEKHyun-Jin PARK∗Hye In YANGSe-In PARK and Woo-Jung CHOI∗

1Department of Rural and Bio-systems Engineering(BK21),Chonnam National University,Gwangju 61186(Republic of Korea)

2Department of Renewable Resources,Universityof Alberta,Edmonton,Alberta T6G 2E3(Canada)

3MaxPlanck Institute for Biogeochemistry,Jena 07745(Germany)

4National Institute of Environmental Research,Incheon 22689(Republic of Korea)

5AgriBio Institute of Climate Change Management,Chonnam National University,Gwangju 61186(Republic of Korea)

ABSTRACT Electrical conductivity(EC)of soil-water extracts is commonly used to assess soil salinity.However,its conversion to the EC of saturated soil paste extracts(ECe),the standard measure of soil salinity,is currently required for practical applications.Although many regression models can be used to obtain ECe from the EC of soil-water extracts,the application of a site-specific model to different sites is not straightforward due to confounding soil factors such as soil texture.This study was conducted to develop a universal regression model to estimate a conversion factor(CF)for predicting ECe from EC of soil-water extracts at a 1:5 ratio(EC1:5),by employing a site-specific soil texture(i.e.,sand content).A regression model,CF=8.910 5e0.010 6sand/1.298 4(r2=0.97,P<0.001),was developed based on the results of coastal saline soil surveys(n=173)and laboratory experiments using artificial saline soils with different textures(n=6,sand content=10%–65%)and salinity levels(n=7,salinity=1–24 dS m−1).Model performance was validated using an independent dataset and demonstrated that ECe prediction using the developed model is more suitable for highly saline soils than for low saline soils.The feasibility of the regression model should be tested at other sites.Other soil factors affecting EC conversion factor also need to be explored to revise and improve the model through further studies.

KeyWords:coastal saline soils,electrical conductivity prediction,reclaimed tideland,regression model,sand content,saturation percentage,soil salinity

INTRODUCTION

Salt accumulation in arable land is one of the constraints in sustainable food production(Eynardet al.,2005;Butcheret al.,2016).It is estimated that approximately 20%of total croplands and 33%of irrigated croplands are under salinization due to improper agricultural management(Singh,2015;Nachshon,2018).In addition,agriculture is expanding into coastal saline soils to meet increasing food supply demands(Limet al.,2020).Soil salinity also affects greenhouse gas emissions(Ghoshet al.,2017)by influencing soil microbial activity(Elmajdoub and Marschner,2015).Therefore,monitoring soil salinity is critical to manage saline soils for sustainable food production while mitigating greenhouse gas emissions under climate change(Abrolet al.,1988;Zhaoet al.,2020).

Soil salinity is conventionally estimated by measuring electrical conductivity(EC)of soils,and several methods are available for EC measurement,including saturated paste extraction(US Salinity Laboratory Staff,1954),soil-water extraction at various ratios(Sonmezet al.,2008),electromagnetic induction(Farzamianet al.,2019),dielectric permittivity measurement(Hilhorst,2000),and satellite remote sensing(Zhanget al.,2021).Among these,the EC of saturated paste extracts(ECe)is currently the standard method and is widely accepted because it reflects the salinity of soil solutions,which directly affects plant growth(Rhoadeset al.,1989).However,saturated paste extraction requires more specific skills to correctly determine saturation points,and is consequently labor-intensive and time-consuming(Al-Busaidiet al.,2006).In addition,measuring ECeis costly when the number of samples is high or when frequent monitoring is required(Aboukila and Norton,2017).For these reasons,many studies have attempted to obtain ECefrom the EC of diluted soil-water extracts at various soil:water mass ratios of 1:1(EC1:1),1:2(EC1:2),1:2.5(EC1:2.5),and 1:5(EC1:5)(Liuet al.,2006;Sonmezet al.,2008;Khorsandi and Yazdi,2011;Aboukila and Abdelaty,2017;Aboukila andNorton,2017;Kargaset al.,2018;Gharaibehet al.,2021).The preference for a specific soil:water mass ratio differs among countries;for example,a ratio of 1:5 is preferred in Australia,China,Central Asia,and South Korea(Shirokovaet al.,2000;Leeet al.,2003),whereas a ratio of 1:1 is more commonly used in USA and Canada(Hogg and Henry,1984;Zhanget al.,2005;Heet al.,2013).

Many studies have reported statistically significant correlations between ECeand EC of soil-water extracts;for example,for EC1:5,the EC conversion factor(CF)has been reported to be 5.0–11.7,based on the slope of correlations between ECeand EC1:5(Sonmezet al.,2008;Chi and Wang,2010;Khorsandi and Yazdi,2011;Heet al.,2012;Aboukila and Abdelaty,2017;Aboukila and Norton,2017;Kargaset al.,2020).Such a wide range of CFs suggests that it is unsuitable to apply a conversion factor established in one study to other sites.Variations in CFmight be associated with differences in soil properties such as soil texture(Monteleoneet al.,2016),type of salt present(Richard and Gouny,1965),gypsum content(Khorsandi and Yazdi,2011),type of clay(Sonmezet al.,2008),and ionic composition(Parket al.,2019).Among the confounding factors associated with CF,soil texture has received more attention(Hogg and Henry,1984;Slavich and Petterson,1993;Khorsandi and Yazdi,2007;Sonmezet al.,2008;Gharaibehet al.,2021).This is because soil texture directly influences soil saturation percentage(SP),which determines the degree of dilution of soil-water extracts relative to saturated paste extracts.For instance,the degree of dilution of 1:5 soil-water extracts relative to saturated paste is greater for coarse-textured soils,which have lower SP than fine-textured soils(Rhoades,1996;Gharaibehet al.,2021).Although a few studies have addressed variations in CFwith soil texture under field conditions(Slavich and Petterson,1993;Gharaibehet al.,2021),mechanistic understanding of the relationship between soil texture and CFis lacking because no study has reported quantitative changes in CFwith soil texture(e.g.,sand content in the present study)under controlled experimental conditions to rule out other compounding factors.This information might be helpful for developing site-specific CFby employing soil texture parameters in a regression model to estimate CF.

This study was conducted to develop a regression model to estimate a texture-specific CFfor obtaining ECefrom EC1:5.It was hypothesized that CFwould gradually increase with increasing sand content,as coarser soils have a lower SP and thus a greater degree of dilution compared to finer soils.In this study,we performed a series of experiments.In Experiment 1,we explored the effects of sand,silt,and clay contents on the ratio of ECeto EC1:5(EC ratio)using data of field soils collected from coastal saline areas.In Experiment 2,as sand was more closely correlated with EC ratio than clay and silt in Experiment 1,a regression model that was responsive to sand content was developed using the relationship between sand content and CF of differently textured soils.For this,artificial soils with various textures(n=6)and salinity levels(n=7)were prepared by manipulating soil texture(by mixing sand and clay)and salinity(by adding salts).The developed equation was then calibrated with the dataset from Experiment 1 to correct the CF.In Experiment 3,the calibrated regression equation was applied to an additional dataset from three independent sites,to validate the applicability and to identify any limitations of the equation.

MATERIALS AND METHODS

Characteristics of reclaimed tideland sites

Saline soil samples were collected from rice(Oryza sativaL.)paddy fields in reclaimed tidelands(RTLs)in coastal areas in southern(five sites for model development)and western(three sites for model validation)regions of South Korea(Fig.1).The study area has a typical humid temperate climate with a monsoon period in the summer.During the last three decades in South Korea,the annual mean temperature was 13.6◦C and annual precipitation was 1 430 mm(KMA,2018).High salinity in the study sites was not developed through secondary salinization,which is often found in arid and semi-arid regions where salts are rarely removed by leaching due to low rainfall and high evaporation(Singh,2015).Instead,coastal saline soils are classified as primary salt-affected soils associated with natural salt accumulation(Pitman and Läuchli,2002).

Coastal RTL soils are characterized by high salinity and shallow groundwater levels,and thus these RTL soils are used for rice cultivation under waterlogged conditions during summer seasons,producing 22.1%of national rice production in South Korea(Limet al.,2020).Rice plants are not salt-tolerant and rice growth is likely to be hampered when ECeis>3.0 dS m−1,with up to 50%of yield loss expected at 6–7 dS m−1(Ayers and Westcot,1976;Francois and Maas,1999).However,during rice growth,excessive salts temporarily leach down below the rooting zone under waterlogged condition,maintained by periodical irrigation of less saline water in these areas(Limet al.,2020).It has been reported that soil salinity decreases with rice cultivationviasalt removal through leaching under rainfall and irrigation in the studied RTLs(Limet al.,2020).However,soil salinity in the RTLs might be also affected by salt invasionviacapillary rise of saline groundwater due to sea water intrusion(Yuet al.,2014;Pereiraet al.,2019).

Experiment 1:Effects of soil texture and other properties on EC ratio

To explore potential effects of soil texture on CF,soilsamples(n=173)were collected from five RTLs in the southern coastal region of South Korea(Fig.1).These five RTLs were Goheung,Youngsangang,Gunnae,Samsan,and Bojeon,with reclaimed land areas of 3 100,10 110,1 381,420,and 296 ha,respectively.These RTLs were constructed for<25 years and managed by the Korean government through intensive soil salinity monitoring.

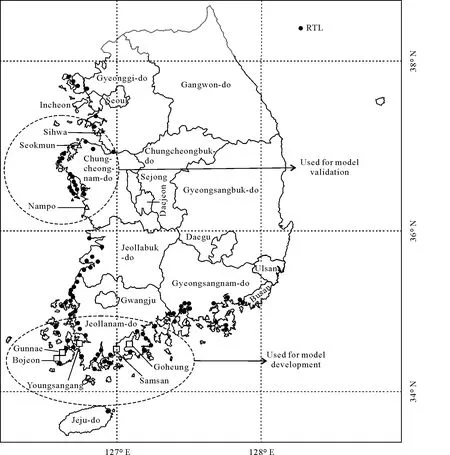
Fig.1 Geographical distribution of the studied reclaimed tidelands(RTLs)(n=91 and area=186 639 ha)along the coastal regions of South Korea.The locations of RTLs from which soil samples(n=458)were collected for regression model development and validation are indicated by square and triangle symbols,respectively.

Soil samples(approximately 5 kg for each sample)were collected from the surface(0–20 cm)of paddy fields(n=173)in the five southern coastal RTL areas.The samples were air-dried,sieved(<2 mm),and used for analysis(Table I).Particle size distribution was determined using the pipette method(Gee and Bauder,1986).Geometric mean particle diameter(dg,mm)was calculated using the following equation(Shirazi and Boersma,1984):

wherefc,fsi,andfsare the contents(%)of clay,silt,and sand fractions,respectively,andMc,Msi,andMsare the mean diameters of clay(0.001 mm),silt(0.026 mm),and sand(1.025 mm),respectively,which were empirically taken for USDA soil texture classification(Chang and Cheng,2018).

Electrical conductivity(EC1:5and ECe)was analyzed following conventional methods(Rhoades,1996)with a conductivity meter(Orion 3 STAR,Thermo Fisher Scientific,Korea).Saturated paste extracts for ECewere obtained using a vacuum extractor(SampleTek 24VE,MAVCO Industries,USA).The relationship between EC1:5and ECe(n=173)was assessed with a linear regression analysis to obtain the mean EC ratio from the slope,which is conventionallyreferred to as CF.The effects of soil particle size distributions on EC ratio were assessed by correlation analysis(n=173)between EC ratio and the contents of sand,silt,and clay.To investigate the effects of other soil properties,such as soil organic matter and cation exchange capacity(CEC),on EC ratio,soil organic C(SOC)content and CEC were also determined.The SOC content was determined with the combustion method(Nelson and Sommers,1996)using an elemental analyzer(FLASHEA-1112,Thermo Fisher Scientific,USA),after finely grinding the soil samples with a ball mill(MM-200,Retsch GmbH,Germany).The CEC was determined using the ammonium acetate(pH 7)method(Nelson and Sommers,1996).

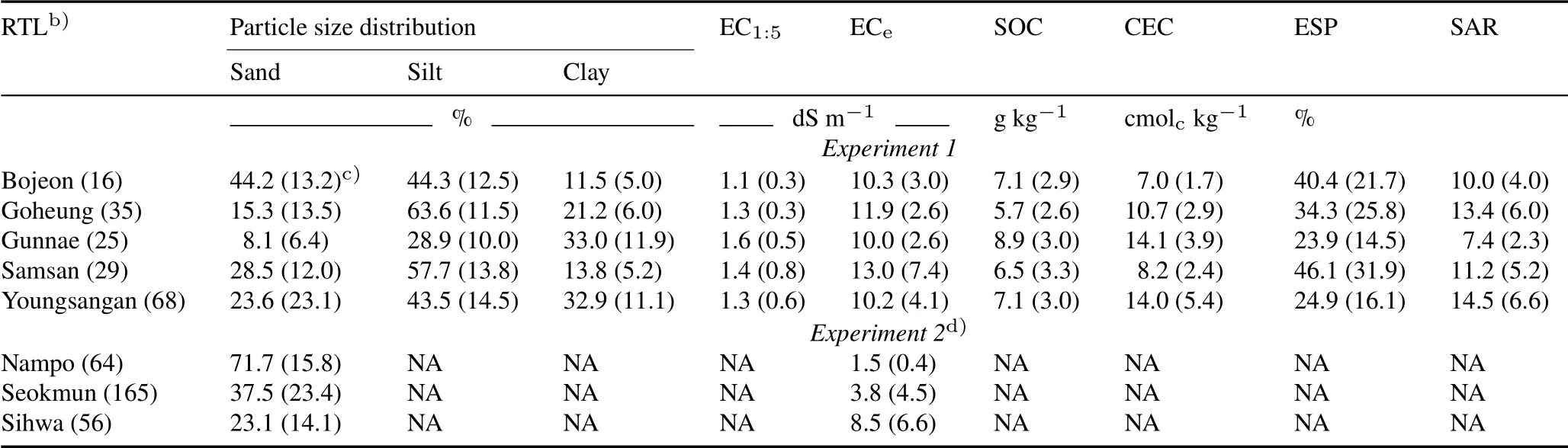
TABLE IPropertiesa)of the reclaimed tideland(RTL)soils collected from coastal regions of South Korea for model development(Experiment 1)and validation(Experiment 2)

Experiment 2:Development of a regression model using sand content as a parameter to determine EC conversion factor specific to sand content

A quantitative relationship between soil texture(i.e.,sand content as a representative of soil texture)and CFwas explored using artificial soils with linear gradients of soil texture and salinity.Approximately 500 kg of non-saline(ECe=0.93 dS m−1)soil with low sand and clay contents(sand:silt:clay=12.0:62.1:25.9)was collected from the surface(0–20 cm)of an experimental farm(126◦53′52′′E,35◦10′24′′N)of Chonnam National University,Gwangju,Korea.The soil was classified as Fluvaquetic Endoaquepts according to USDA Soil Taxonomy(RDA,2000).The soils were air-dried and passed through a 4-mm sieve,and 3 kg of each soil sample was placed in a plastic container(28 cm×20 cm×15 cm).Any visible impurities,including plant residues and gravel,were removed during sieving.A total of 126 soil containers were prepared for six soil texture groups and seven salinity levels in triplicate.Different amounts of silicate sand and clay(1:1 mixture of kaolinite and illite)were added to the soils in the containers to prepare six textures groups:silty clay loam,silt loam,clay loam,loam,sandy clay loam,and sandy loam(Table II).Silicate sand(0.05–1.4 mm in diameter),kaolinite(<0.002 mm),and illite(<0.002 mm)were purchased from a construction company(TM Inc.,Korea).Silicate sand was washed with tap water to remove any salt and oven-dried at 105◦C before use.

Salt solutions of seven different concentrations(approximately 1.3,2.5,4.7,9.1,13.2,17.3,and 23.6 dS m−1)were prepared by dissolving chemical grade salts(Junsei,Japan)in deionized water.The solution with EC of 23.6 dS m−1was prepared by dissolving NaCl(5.1 g L−1),NaNO3(5.1 g L−1),CaSO4·2H2O(1.7 g L−1),KNO3(1.7 g L−1),and MgCl2(3.4 g L−1).Solutions with lower salt concentrations were prepared by diluting the solution with EC of 23.6 dS m−1using deionized water.The final EC values of the solutions were determined using a conductivity meter.The EC levels and ionic compositions of the solutions were determined by considering the reported salinity and cation concentrations of RTL soils in South Korea(Limet al.,2020).The soilsand mixture was then treated with 1 500 mL of the target salt solution to saturate the mixture.The containers were uncovered and placed in a room for 2 months to ensure the stabilization of the mixture and equilibrium between the solid mixture and the salt solution.As the water content of the mixture was still high after 2-month of aging,the containers were oven-dried at 40◦C for 7–10 d.

The dried soils were passed through a 2-mm sieve and analyzed for EC1:5and ECefollowing the methods describedabove.For ECemeasurement,to minimize experimental errors among replicates,a saturation point was pre-determined for each soil texture group using an extra soil sample,and the same amount of water was added to saturate the same textured soils.The amounts of water required for saturating 300 g of soil were 115.0,108.0,93.5,81.8,72.2,and 59.0 mL for silty clay loam,silt loam,clay loam,loam,sandy clay loam,and sandy loam,respectively(equivalent to SP of 48.3%(volume/volume),46.8%,40.5%,35.4%,31.3%,and 25.6%,respectively).

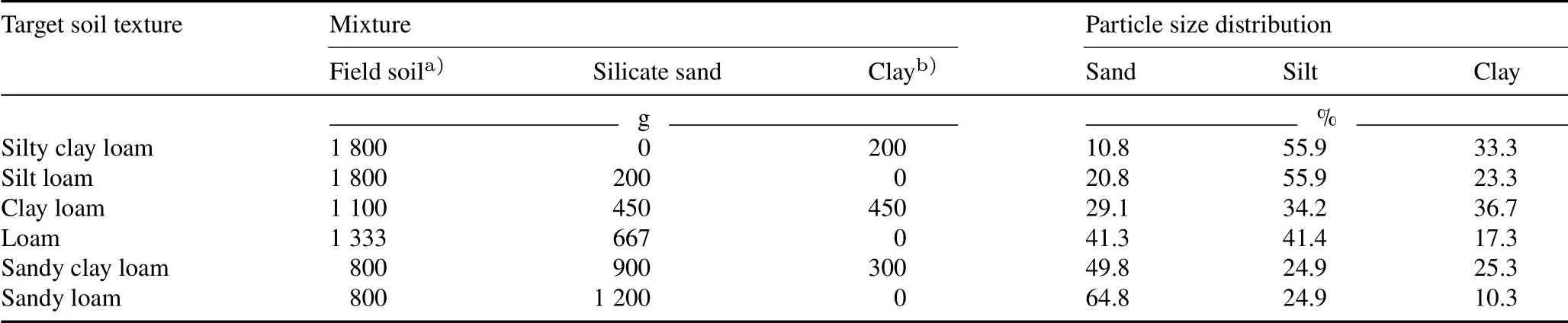
TABLE IIDetails of different soil textures prepared for Experiment 2

For silt loam(sand=20.8%)and sandy loam(sand=64.8%)soils,the solutions obtained from ECeextraction were further analyzed for concentrations of cations(Na+,Mg2+,and Ca2+)using an atomic absorption spectrometer(Analyst 800,Perkin Elmer,USA),to investigate the potential effects of sodium adsorption ratio(SAR)on CF,as Na+could be more easily released into saturated solutions than other cations due to its low sorption ability onto soil particles(Brady and Weil,2002;Jalaliet al.,2020).

The CFfor each soil texture group was obtained from the slope of a regression analysis(n=7)between EC1:5and ECe.A regression model to calculate CFresponsive to sand content was developed by regression analysis(n=6)using sand content as an independent variable and the CF at the corresponding sand content as a dependent variable.The developed model was calibrated using the dataset of Experiment 1.

Experiment 3:Validation of regression model for EC conversion

To validate the regression model,another set of soil samples were collected from three RTL sites located in western coastal areas,different from the sites used for Experiment 1(Fig.1).These three RTLs were Sihwa(typical soil texture was loam,n=56),Seokmoon(sandy loam,n=165),and Nampo(sand,n=64),with reclaimed land areas of 3 636,2 780,and 2 285 ha,respectively.

The soil samples were collected and analyzed for sand content and ECeusing the methods described above(Table I).The measured ECe(ECm)and the predicted ECe(ECp)from the regression model were compared using a pairedt-test with a null hypothesis that there is no difference between the ECpand ECmvalues.The performance of the model was evaluated using coefficient of determination(r2)and root mean square error(RMSE)(Heet al.,2013)of the correlation between the ECpand ECmvalues.The ECeprediction error(%)was calculated as a percentage difference from ECm:

Statistical analyses

For statistical analyses,data were tested for homogeneity of variance and normality of distribution using Levene’s test and Kolmogorov-Smirnov test,respectively.All data were found to be normally distributed with homogenous variances.All statistical analyses were performed using IBM SPSS Statistics 23(IBM Corp.,USA).Statistical significance was set atP=0.05.In the regression analysis between EC1:5and ECe,theY-intercept was forced to the origin,i.e.,(0,0)coordinate,because soils with EC1:5of 0 dS m−1should have ECeof 0 dS m−1.

RESULTS AND DISCUSSION

Experiment 1:EC ratio in relation to soil texture,SOC and CEC

In Experiment 1,there was a linear correlation(slope=8.1,r2=0.73,P<0.001)between EC1:5and ECeacross all soil samples(Fig.2).The slope was within the range(5.0–11.7)reported in other studies(Sonmezet al.,2008;Chi and Wang,2010;Khorsandi and Yazdi,2011;Heet al.,2012;Aboukila and Abdelaty,2017;Aboukila and Norton,2017;Kargaset al.,2020).The EC ratios were correlated with soil particle size distribution.The relationship was positive for sand content(r2=0.35,P<0.001),but negative for silt(r2=0.11,P<0.001)and clay(r2=0.26,P<0.001)contents(Fig.3a–c),suggesting that soil texture might be a key factor affecting CF(Hogg and Henry,1984;Slavich andPetterson,1993;Sonmezet al.,2008;Gharaibehet al.,2021).Among the particle size groups,sand was more strongly correlated with the EC ratio than silt and clay,as indicated by the greaterr2value.Thedgwas also positively correlated(r2=0.38,P<0.001)with the EC ratio(Fig.3d),but the correlation was not significantly better than that between the EC ratio and sand content.

Fig.2 Regression analysis between EC1:5 and ECe of soils(n=173)collected from five reclaimed tidelands(RTLs)in southern coastal region of South Korea for developing regression models(Experiment 1)for EC conversion.Locations of these RTLs are indicated in Fig.1.EC1:5=electrical conductivity(EC)of soil-water extracts at a 1:5 mass ratio;ECe=EC of saturated soil paste extracts.

The EC ratio was negatively correlated with CEC(r2=0.29,P<0.001)and SOC content(r2=0.07,P<0.001)(Fig.3e,f).This can be explained by the effects of clay on CEC and SOC,as CEC and SOC content are often positively correlated with clay content(Brady and Weil,2002).In the present study,there were also significant correlations of clay content with CEC(r2=0.67,P<0.001)and SOC content(r2=0.07,P<0.001).

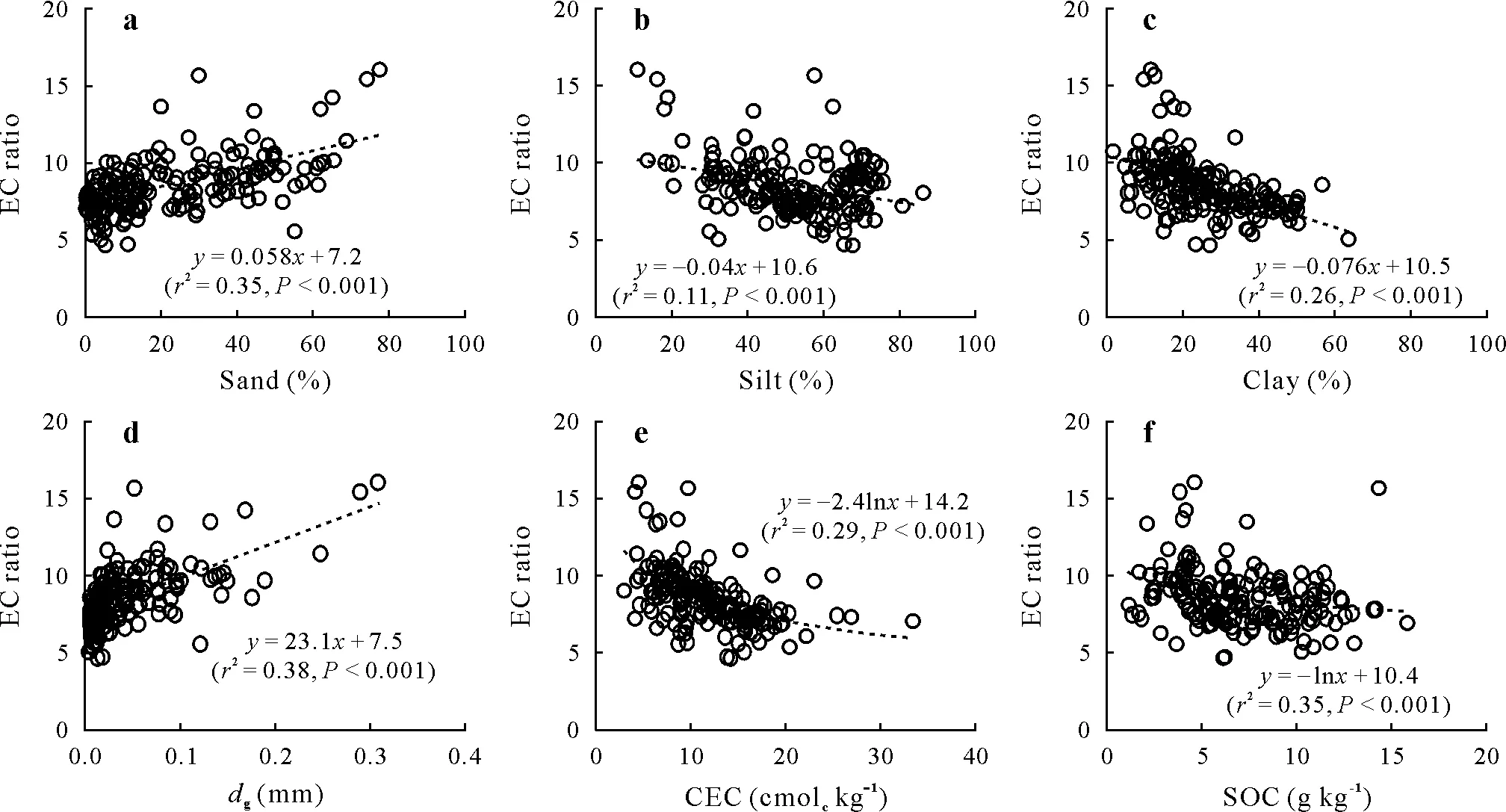
Fig.3 Correlations of ECe to EC1:5 ratio(EC ratio)for soils(n=173)used for regression model development(Experiment 1)with their properties:sand content(a),silt content(b),clay content(c),geometric mean particle diameter(dg)(d),cation exchange capacity(CEC)(e),and soil organic carbon(SOC)content(f).ECe=electrical conductivity(EC)of saturated soil paste extracts;EC1:5=EC of soil-water extracts at a 1:5 mass ratio.

Experiment 2:Development of regression model to predict ECe from EC1:5

In Experiment 2,EC1:5and ECewere also positively correlated(r2>0.98,P<0.001)for all soil textures with different slopes,and thus the CFdiffered with soil texture(Fig.4a).The CF tended to increase from 10.3 to 18.4 with increasing sand content(Fig.4b)and decreasing SP(Fig.4c).This is because the SP of coarser soils is lower than that of finer soils(Kargaset al.,2018;Gharaibehet al.,2021),which was also supported by the negative relationship between SP and sand content(SP=−0.45sand+54.1,r2=0.99,P<0.001,n=6,data not shown).Gharaibehet al.(2021)reported that CF(or EC ratio)increased with increasing sand content,and that a CF>15 was found when the sand content was higher than 40%.These results suggest that in the present study,higher sand content resulted in a greater CFthan those reported in other studies(Sonmezet al.,2008;Chi and Wang,2010;Khorsandi and Yazdi,2011;Aboukila and Abdelaty,2017;Aboukila and Norton,2017).Therefore,our study,together with the study of Gharaibehet al.(2021),suggests that SP might be a critical factor affecting CF.Gharaibehet al.(2021)further developed amultiple regression model to estimate SP using both sand and clay contents.However,in the present study,SP was not significantly correlated with clay content(SP=0.62clay+22.8,r2=0.47,P=0.133,n=6,data not shown).Thus,a multiple regression analysis was not performed using both sand and clay contents.Multiple regression models assume that all independent variables(e.g.,sand and clay)are correlated with the dependent variables(e.g.,CF)(Ott and Longnecker,2010);thus,the relationships observed between the variables in our dataset violate this assumption.

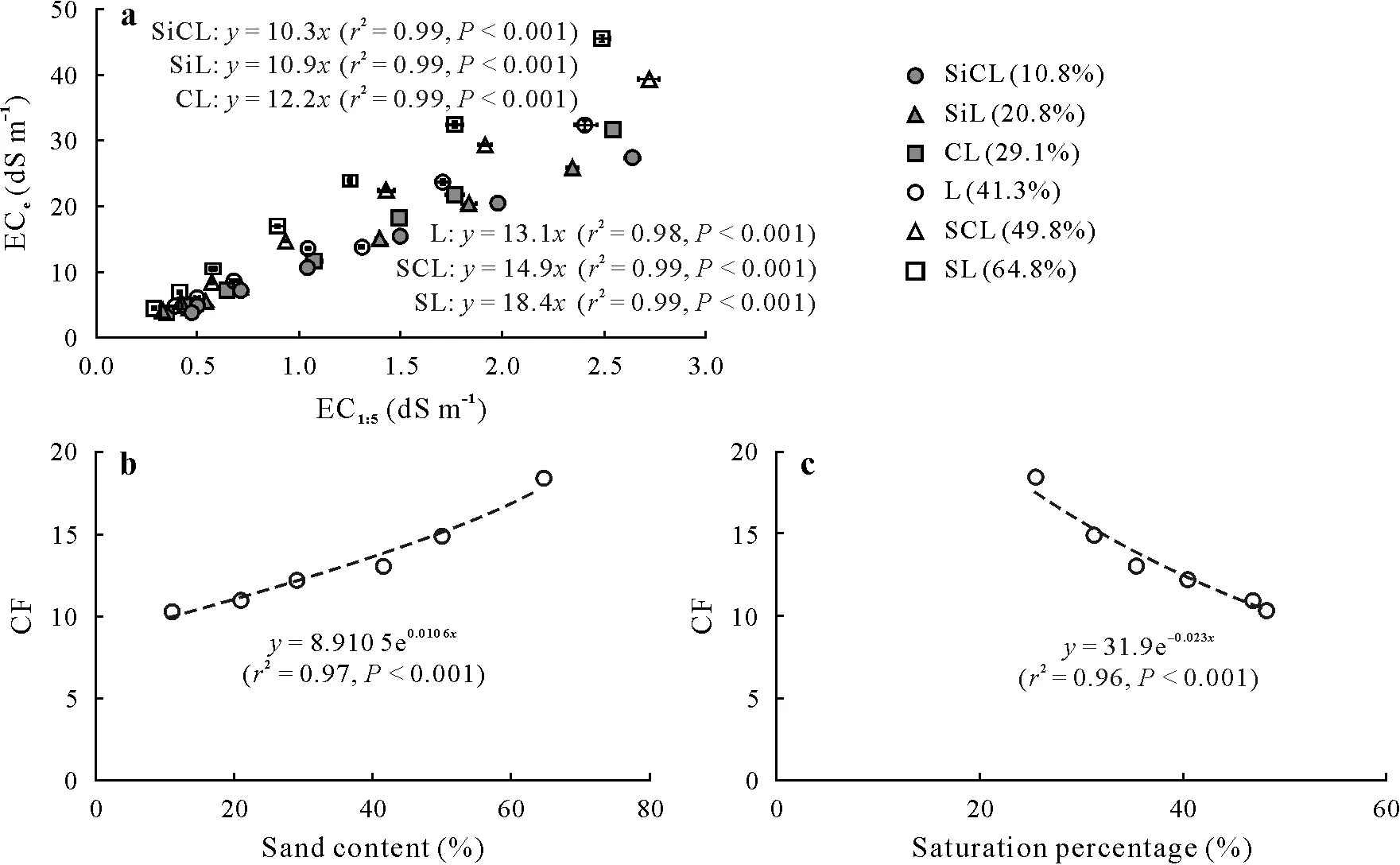
Fig.4 Relationships between EC1:5 and ECe(n=7)(a),between electrical conductivity(EC)conversion factor(CF,the slope of ECe vs.EC1:5 in subfigure a)and sand content(n=6)(b),and between CFand saturation percentage(n=6)(c)of artificial saline soils with different salinity levels in Experiment 2.For subfigure a,the values in parentheses beside soil texture(SiCL=silty clay loam;SiL=silt loam;CL=clay loam;L=loam;SCL=sandy clay loam;SL=sandy loam)are sand content;data are the means of triplicates with standard errors of the means indicated by horizontal and vertical bars across symbols.For subfigures b and c,no standard error bar is available.The regression equation in subfigure b was used for developing a model to estimate EC conversion factor using sand content as a variable.EC1:5=EC of soil-water extracts at a 1:5 mass ratio;ECe=EC of saturated soil paste extracts.

The increasing pattern of CFwith increasing sand content was best expressed as an exponential function of sand content:

Although a few studies have reported a tendency of CFto increase from finer to coarser soils(Hogg and Henry,1984;Sonmezet al.,2008),our study first reported a quantitative relationship between sand content and CFin controlled experiments by ruling out other confounding factors.However,in the present study,CFalso showed an increasing pattern(r2>0.64,P<0.05)with increasing SAR(Fig.5a)by influencing ECe(r2>0.99,P<0.001)(Fig.5b).This result suggests that SAR needs to be considered when developing a more precise regression model for CFestimation,as Na+is a predominant cation in coastal RTLs(Limet al.,2020).As SAR was not included in the regression model in the present study due to the limitation of the original experimental design,the effect of SAR on CFshould be investigated in a future study.

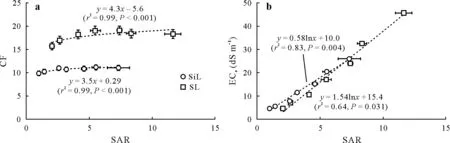
Fig.5 Relationships between sodium adsorption ratio(SAR)and electrical conductivity(EC)conversion factor(CF,the slope of ECe vs.EC1:5 in Fig.4a)(n=7)(a),and between SAR and ECe(n=7)(b)of artificial saline soils with various textures(SiL=silt loam;SL=sandy loam)and salinity levels in Experiment 2.Data are the means of triplicates with standard errors of the means indicated by horizontal and vertical bars across symbols.ECe=EC of saturated soil paste extracts;EC1:5=EC of soil-water extracts at a 1:5 mass ratio.

When the exponential equation,i.e.,Eq.3,was applied to the dataset of Experiment 1,the predicted ECewas correlated(r2=0.76,P<0.001)with the measured ECewith a slope of 1.298 4,indicating that the regression model overestimated ECeby 29.8%on average(Fig.6).Therefore,for correction of the bias,the exponential function was revised to:

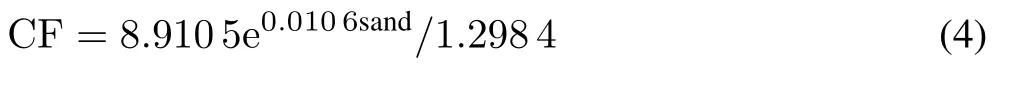
When the calibrated function was applied,a slope of 1.0 was achieved,and the RMSE was reduced from 13.8 to 1.06(Fig.6).

Fig.6 Relationships between measured and predicted ECe for the soils(n=173)collected from five reclaimed tidelands(RTLs)in southern coastal region of South Korea,for the development of a regression model for electrical conductivity(EC)conversion.The locations of these RTLs are indicated in Fig.1.Original prediction values are the results of direct application of the regression model(Eq.3)and revised prediction values are the results of applying the calibrated regression model(Eq.4).ECe=EC of saturated soil paste extracts;RMSE=root mean square error.

Experiment 3:Validation of regression model

The calibrated regression model overestimated ECeby 9%–57%as indicated by the slope of the regression between measured and predicted ECe(Fig.7).However,the predicted ECewas linearly correlated with the measured ECe,with differentr2and RMSE values among the three RTLs(Fig.7).Among the three RTLs,the performance of theregression model was the best for Sihwa(Fig.7a),followed by the Seokmoon(Fig.7b)and Nampo(Fig.7c)based on the slope andr2values.This pattern was associated with both sand content and ECelevels of the soils,as indicated by better performance of the model for RTL soils with high ECeand low sand content(e.g.,Sihwa)than for soils with low ECeand high sand content(e.g.,Nampo)(Table I).The error of ECeprediction increased with increasing sand content(Fig.8a)and with decreasing measured ECe(Fig.8b).Sand content and ECeare often inversely correlated(Limet al.,2020),as also indicated by the negative relationship observed between sand content and ECe(Table I,ECe=1 072.9sand−1.548,r2=0.998,P=0.027)in the present study.This is because coarser soils are likely to have lower salinity than finer soils due to faster desalinizationviaenhanced salt leaching through macropores and prevention of capillary rise of salts(Limet al.,2020).

Fig.7 Relationships between measured and predicted ECe(computed using the calibrated regression model,Eq.4)for the soils,with different textures and salinity levels,collected from three reclaimed tidelands(RTLs)in western coastal region of South Korea:Sihwa(n=56)(a),Seokmoon(n=165)(b),and Nampo(n=64)(c).The locations of these RTLs are indicated in Fig.1.ECe=electrical conductivity of saturated soil paste extracts.RMSE=root mean square error.

Owing to co-variations of sand content and ECe,it was not straightforward to discriminate their relative contributions to the ECeprediction errors.However,larger errors were distributed densely at ECevalues below 5 dS m−1,compared to those at ECeabove 5 dS m−1(Fig.8b).The mean of the absolute errors at ECevalues below 5 dS m−1was 56.4%(n=211),whereas that at ECevalues above 5 dS m−1was 24.0%(n=74).This result suggests that the developed model might be more feasible for highly saline soils with ECevalues higher than 5 dS m−1.Obviously,there must be some errors resulting from variations in CEC and SOC content during model calibration,as the ratios of ECeto EC1:5were also affected by these two soil variables in Experiment 1(Fig.3d,e).In addition,the equilibration method and time might also contribute to the errors,since less saline soils(ECe<3–4 dS m−1)require longer equilibration time for stable EC measurement(Heet al.,2012;Kargaset al.,2018,2020).The equilibration method also affects EC(Heet al.,2012),eventually affecting the EC conversion factor(Kargaset al.,2020).

Fig.8 Relationships between errors of ECe prediction and sand content(a)and ECe measured(b)for the soils collected from three reclaimed tidelands(RTLs)in western coastal region of South Korea:Sihwa(SH)(n=56),Seokmoon(SM)(n=165),and Nampo(NP)(n=64).The regression equations were obtained using all data(n=285)pooled across three RTLs.Larger errors were often distributed at ECe values below 5 dS m−1(mean of the absolute errors was 56.4%,n=211),whereas smaller errors were found at higher ECe values over 5 dS m−1(mean was 24.0%,n=74).ECe=electrical conductivity of saturated soil paste extracts.

Implications for soil salinitymonitoring

As the CFis affected by many soil factors,application of a site-specific regression model to different sites might be unfeasible to predict ECefrom EC1:5.However,as the regression model developed in the present study employed site-specific sand content as a parameter,the model could be used for preliminary estimation of ECeusing sand content and EC1:5at any site when the site-specific CFis unavailable.As soil texture is a basic soil characteristic that is extensively surveyed and thus might be easily obtained,additional determination of sand content might not be required in most cases.Therefore,the model developed in the present study can be applied to a range of soil texture groups when sand content is available.However,it should be noted that the model performance was poor for soils with low salinity.

The developed model can also be applied for ECeestimation using non-destructive remote sensing technologies,such as electromagnetic induction(Farzamianet al.,2019)and satellite remote sensing(Zhanget al.,2021).As a large number of ECedatasets are required for evaluating the feasibility of remote sensing data,it might be possible to employ the regression model for preliminary calibration of data obtained from remote sensing.If necessary,revising the empirical coefficient of the model,by testing the regression model using representative soil samples,might improve the performance of the EC conversion regression model to calibrate remote sensing data.

CONCLUSIONS

A regression model to estimate site-specific CFfor the conversion of EC1:5to ECewas developed using the relationship between sand content and CF.As the model employed soil-specific sand content,it might be possible to obtain soil-specific CFwhen sand content is available,particularly for highly saline soils.However,there are still uncertainties in predicting ECeusing the developed regression model,which was only responsive to sand content;other soil factors(e.g.,SAR in the present study)should also be considered.Nevertheless,this study provides a foundation for further studies on the prediction of ECeusing EC1:5,by suggesting the necessity and possibility of developing a soil-type specific CF.To improve ECeprediction,further studies are necessary to test the feasibility of the regression model developed in the present study and to explore the effects of other soil factors on site-specific CF.

ACKNOWLEDGEMENTS

This work was carried out with the support of the Cooperative Research Program of Agriculture Science and Technology Development,Rural Development Administration,Republic of Korea(No.PJ0138732021).The scholarship from the BK21 Project(Education and Research Unit for Climate-Smart Reclaimed-Tideland Agriculture)of the Ministry of Education,Republic of Korea is also acknowledged.