多参数下铁路接触网避雷线绕击率的计算
2022-12-14李勇军
李勇军
(广西沿海铁路股份有限公司钦州供电段,广西钦州 535000)
引言
我国高速铁路快速发展,不同地区的气候、地理条件差异很大,若防雷接地系统设计不合理,将会很容易遭受雷击。一旦遭受雷击,将会造成行车事故威胁乘客人身安全[1,2]。国内已有数条铁路线路发生雷电袭击,都造成了很严重的经济和人员方面的损失[3,4]。铁路防雷已经成为当前研究重点。
随着雷击事故发生的频率越来越高,铁路系统避雷线设计也逐渐引起了人们的注意,我国近几年在铁路系统雷击领域也展开了越来越多的研究。文献[5-7]对我国铁路系统雷电防护体系进行了深入分析和研究,并且提出了参考电力系统设计架设专用避雷线,或者选择将PW线回流线高度提高做避雷线的防雷设计方案,可以明显提升铁路接触网雷电防护性能。文献[8,9]也对高速铁路系统接触网雷击跳闸率的计算方法进行了深入分析和研究。文献[10,11]应用传统电气几何模型分析了铁路系统接触网防雷性能,同时利用传统电力系统中电气几何模型建立了铁路牵引网雷击电气几何模型,并推导出铁路系统牵引网雷击跳闸率计算公式。
本文结合高速铁路系统接触网结构特点,并参考现有避雷线屏蔽计算方法,提出了多参数下降低铁路接触网避雷线绕击率的设计方法,以电气几何模型为基础,考虑多参数下避雷线绕击率的计算,为我国接触网防雷改造提供有效的指导。
1 改进电气几何模型
1.1 击距系数
(1)地线击距
模型计算地线击距主要采用IEEE标准所推荐的公式:

(2)地面击距
雷电放电先导对地面的击距与对输电导线的击距比值为击距系数,在IEEE标准中的计算公式为:
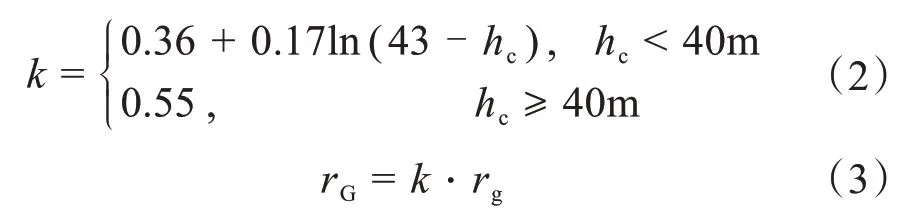
式中,I为雷电流,kA;rg为雷电对避雷线的击距,m;rG为雷电对大地的击距,m;hc为导线平均高度,m。结合地面倾角进行考虑,并根据几何图形数学关系进行推导,可以得到雷电放电地面击距的计算公式为:
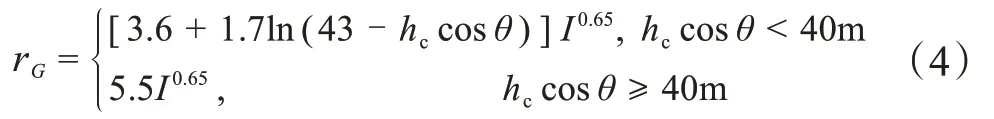
(3)导线击距
考虑架空导线的工作电压及其周期变化特征性,得到铁路系统导线击距计算表达式为:
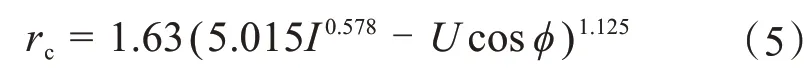
式中,rc为工作电压工况下的导线击距,m;U为导线上工作电压幅值,MV;ϕ为电压相角,取值为0~π;ϕ为随机均匀分布,即f(ϕ)=1/(2π)。
1.2 风速
(1)风压不均匀系数
铁路接触网在同一档距上且在同一时刻不同点上时所承载的风速均不相同,自然风的角度也几乎不会与接触网架设方向成90°角。从《交流电气装置的过电压保护和绝缘配合》的相关规定可知,悬垂绝缘子串的风压不均匀系数αf的计算公式可以表示为:
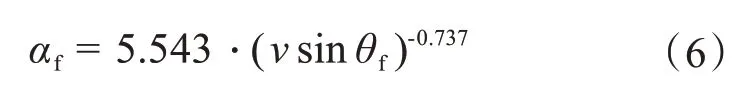
(2)风偏角的计算
目前拟合风速分布的模型比较多,适用于统计描述风速的模型被普遍认为是韦布尔双参数分布模型,风速v的韦布尔分布概率密度函数可以表示为:
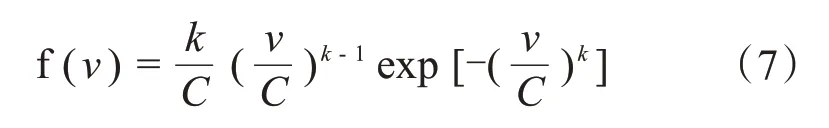
式中,k为形状参数;C为尺度参数,可根据T时间内观测到的10 min最大风速和平均风速计算得到,其近似计算公式可以表示为:

式中,vˉ为平均风速,m/s;vmax为最大风速,m/s;Γ为伽马函数。我国的风速主要分布在0~10m/s,因此取k=2,C=5。
1.3 雷电入射角
传统EGM模型在计算绕击率时,忽略了雷电先导发展的随机性,认为雷电方向始终是竖直向下。暴露弧和屏蔽弧是在垂直于竖直方向的水平面进行投影的,得到暴露弧和屏蔽弧的水平投影长度,从而计算得到线路绕击率。实际上,雷电可能来自不同方向。在计算绕击率时,应该考虑雷电入射角的影响,在计算暴露弧和屏蔽弧的投影长度时,应当是垂直于雷电方向上的投影长度。
Whitehead认为雷电先导接近地面时,雷电入射角是随机的,提出了先导入射角概率密度分布函数:
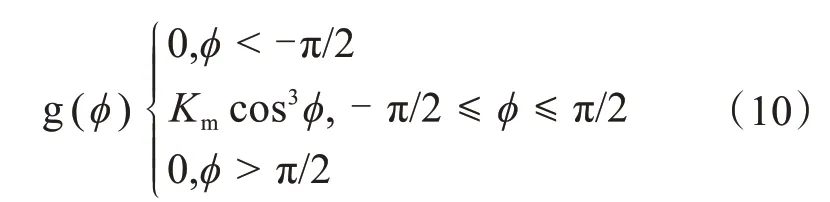
由上式知雷电以[-π/2,π/2]为入射角入射时会存在概率,其他范围内均不会出现概率。而且在区间[-π/2,π/2]内,函数是一个偶函数,只要绝对值相等,那么函数值就相同。可以发现在区间[-π/2,0]和[0,π/2]的结果是完全对称的,因此只需要考虑[0,π/2]即可。在分析入射角概率密度时,采用国际上一般的分析成果,公式如下:
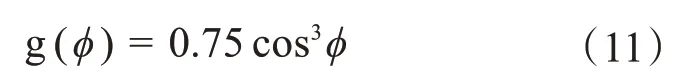
2 多参数绕击率的计算
在计算绕击率时,采用投影法,即将暴露弧和保护弧分别投影到雷电入射的垂直方向,可以通过计算暴露弧投影长度与暴露弧和保护弧投影长度之和的比值来计算绕击率,在考虑坐标变换之后,以及击距系数、风偏、雷电入射角的概率分布,绕击率的计算公式为:

3 绕击性能分析
图1为以高速铁路复线情况下接触网EGM模型[12-17],图1中Rg、RF、RT、Rb分别表示大地击距、馈线击距、接触线击距和避雷线击距。实际上可以通过调整避雷线高度来确保接触网不同导线能被有效屏蔽,利用电气几何模型(EGM)可以有效分析图中避雷线的屏蔽情况。
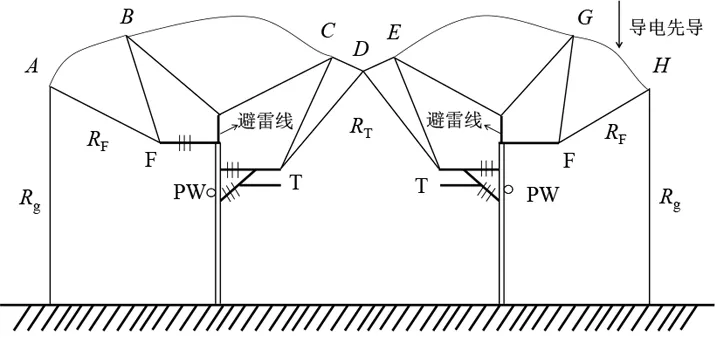
图1 铁路复线情况下接触网EGM模型
目前我国高速铁路牵引供电系统供电方式一般采用AT,通过牵引变电所向高速铁路系统接触网供电时,供电臂长度范围在30 km~50 km。图2为AT供电方式接触网结构示意图。
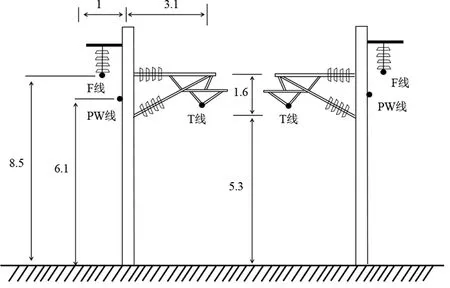
图2 接触网结构示意图
雷击支柱时,F线首先发生闪络,因此可以将F线发生闪络时所对应的雷电流作为反击耐雷水平。各导线的参数如表1所示。
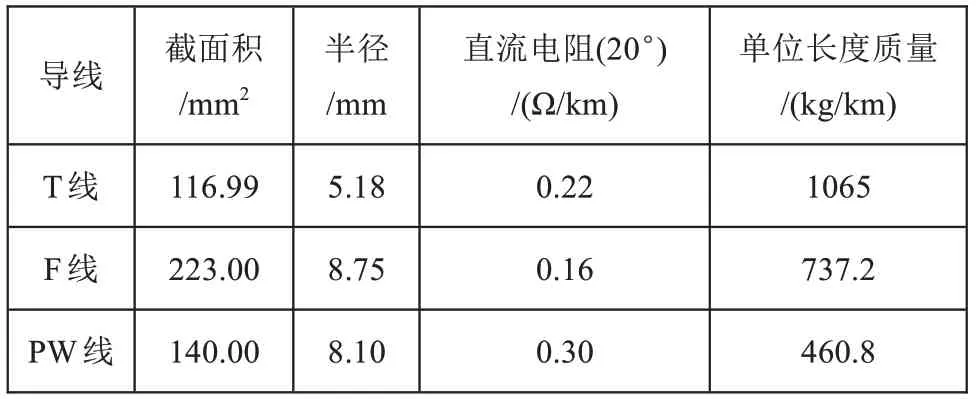
表1 接触网导线参数
3.1 击距系数对绕击率的影响
在经典的EGM模型中,假设当雷电流相同时,大地、导线和避雷线的击距是相同的,在该种模型基础上,能够对实际运行时所遇到的问题进行较好的分析,图3为不同击距系数的情况下铁路雷电绕击率。
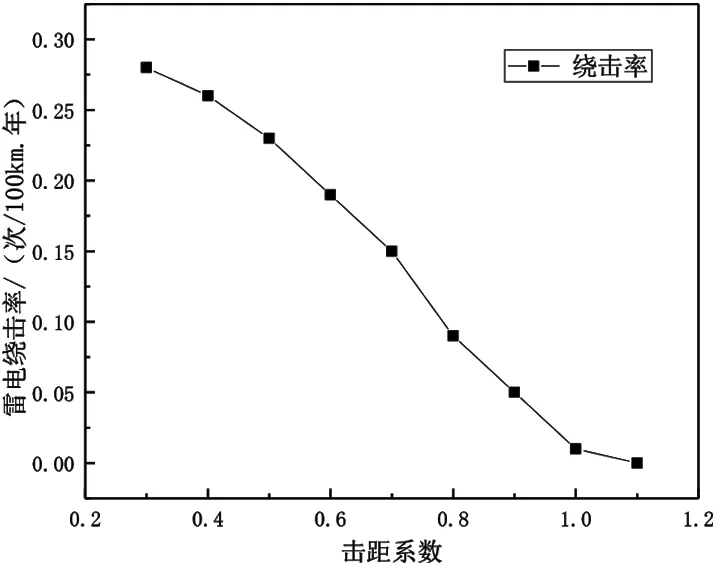
图3 击距系数对绕击率的影响
随着击距系数的逐渐增大,高速铁路中的雷电绕击率会逐渐减少。若还是按照经典EGM模型,将会导致计算的绕击率数值较小,如果不进行改进设计,投入运行后有可能出现安全故障。
3.2 风速对绕击率的影响
在以往的防雷设计中,很少对风速进行分析和研究,很多时候都是直接忽略风速对铁路接触网雷电绕击闪络率的影响。在雷电活动强度以及风速不同的地区,铁路接触网导线和避雷线的高度也很高,有风吹过时,导线和避雷线摆动都比较大,避雷线保护角会增大,容易发生绕击。接触网在不同的风速下其雷击绕击率计算结果如图4所示。
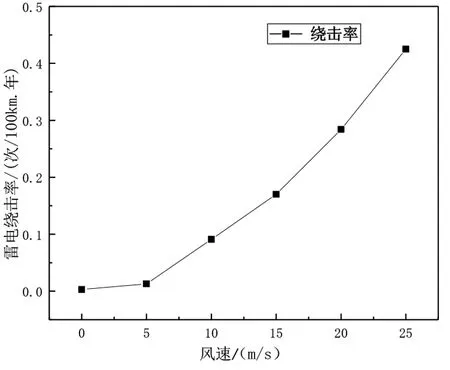
图4 风速对绕击特性的影响
由图4可知,当风速超过10 m/s时,绕击率将会随着风速的增大而明显增加,因此在分析高速铁路接触网耐雷性能时,需要充分考虑沿线的气象条件才能得到更加符合实际情况的结果。随着风速的增加,会导致保护角的增加,同时增加了绕击闪络区,也会使导线离地面高度增加,使导线引雷几率增加,导致绕击率增大。
3.3 雷电入射角对绕击率的影响
在计算线路绕击时,常常认为雷电方向竖直向下,忽略了雷电先导的随机性,这是不够准确的。本研究考虑雷电入射角的影响,当风速为10 m/s时,接触网在不同雷电入射方向时其雷击绕击率计算结果如图5所示。
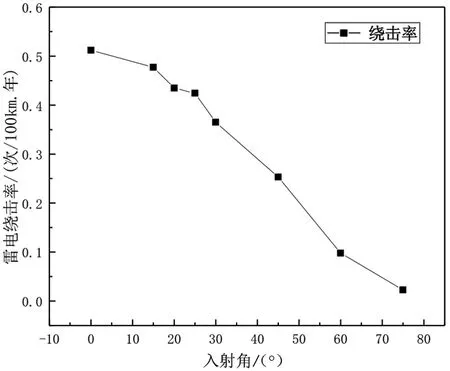
图5 入射角对绕击特性的影响
运用传统方法,不考虑雷电入射角时,雷电绕击率高于φ=0时的绕击率,这是因为传统方法没有考虑雷电竖直向下的概率,认为竖直向下的概率为100%;实际上,考虑雷电入射角时,雷电先导的随机性及其出现的概率,都应考虑。φ=0°时,绕击率为0.521,然而当φ=90°时,绕击率将会接近0。
4 结论
(1)对于考虑击距系数、风速、和雷击入射角的电气几何模型,理论上绕击率的计算比经典电气几何模型更接近实际,为铁路接触网防雷性能分析提供依据。
(2)击距系数的增加会导致绕击率降低,在实际设计当中,可以适当增大击距系数。
(3)随着风速的增加,接触网绕击率呈上升趋势,故在实际工程应用中在风速偏大的地区应添加防舞动措施。
(4)考虑雷电入射角显然更具有实际意义,绕击率随着入射角度的增加而逐渐减少,这也是本模型相比传统的电气几何模型改良之处。
