段塞流对弯管瞬态冲击的三维CFD数值模拟研究

康竞澜， 刘 昉， 侯庆志， 何军龄， 林 磊

(1. 天津大学 建筑工程学院， 天津 300350;2. 西北农林科技大学 水利与建筑工程学院， 陕西 杨凌 712100;3. 苏州热工研究院， 江苏 苏州 215004)

在诸如火电站、核电站等电力或化工工业系统中，会存在大量用于输送高温高压蒸汽的管道。当管路系统由于维护、检修或其他原因而停止工作时，管道中的高温蒸汽因温度降低而凝结成的小水团会在管路系统低洼处逐渐积聚存留，形成静态的液体段塞。一旦系统重新启动，管道上游的瞬时高压蒸汽会将这些段塞瞬间加速，像枪膛内的子弹一样快速射出[1]。当高速运动的段塞撞击到弯管、三通或阀门等管端结构时，将产生巨大的冲击力，可能会对管路造成严重的破坏，从而影响整个系统的正常工作。因此，对管道关键部分(如弯管处)的高速运动段塞的冲击研究尤为重要。目前关于在水平管道或者垂直立管中的稳态段塞流研究已经有了比较成熟的体系和方法[2-3]，而对于弯管中单个段塞流的研究尚未完全展开，尤其是段塞流在弯管处的高维冲击现象值得深入研究。

由于管道中存在的段塞的高风险性，因此需要对其运动状态进行分析。之前的研究表明，作用在弯管上的力主要是由流体运动方向改变所造成的动量转换产生的。段塞流在管道中的流动实际是三维的，但以往的研究主要是基于一维模型，具有较大的局限性。因此为了精准地描述段塞流的运动状态，本文建立了单个段塞在三维空管中的运动及其在弯管处的冲击模型，并将数值模拟结果与试验结果进行了比较，真实准确地分析了段塞在空管中的运动过程以及高速运动段塞对弯管的冲击。

1 段塞流冲击弯管研究现状

最近，针对段塞流冲击弯管的问题进行了综述研究，本节将从试验研究与理论研究两个方面简要阐述对本次研究比较重要的成果。

1.1 试验研究

Fenton 等[4]通过试验最早研究了直径为25 mm的倾斜管道中，弯管因单个液体段塞冲击而产生的作用力。当段塞运动距离大于其自身长度5倍时，气体将击穿段塞从而导致冲击力大幅降低。Neumann等[5]发现当管道气液比小于20%时，便不会发生分层流向段塞流转变的过程，而由此对弯管处的冲击力也可忽略不计。Bozkus等[6]在改进的Fenton 试验装置基础上，发现相对较短的段塞冲击压力曲线呈现单峰，而相对较长的段塞呈现双峰，并把此现象的产生归结于阀门打开时的水锤效应。Owen等[7]进行了段塞流冲击孔板的物理试验，记录了孔板处的压力变化，测得了不同长度段塞流到达孔板时的速度范围在30 m/s到60 m/s不等。

1.2 理论研究

对于段塞流冲击速度的计算，目前已有多种理论模型。Fenton 等通过稳定状态下段塞流的名义速度予以描述，其表达式为

(1)

式中：ρ表示下游的气体密度；A表示管道的横截面积；m为质量流量。Neumann等提出一个相对复杂模型，考虑了驱动气体的动力学性质，却忽略了段塞流的质量损失。Kayhan等[8]运用单步特征线法，分别考虑了恒定滞留系数以及通过试验数据拟合得到的滞留系数，并由此计算了质量损失。最近，Tijsseling等[9]通过考虑段塞前后气液界面的速度差，将段塞的速度分成三个部分，改进了Bozkus的数值模型，取得了较好的效果。

稳态段塞流对固壁的冲击与稳态射流的冲击[10]类似，其表达式为

(2)

其中ρs为段塞密度，Vs为段塞冲击速度。但该模型计算的冲击力远低于试验测得的实际冲击力。Fenton[11]在其1989年论文中提到，在工程应用中弯管处的冲击力可由以下公式计算所得

(3)

上式中第一项为以声速c传播的压力波在弯管处冲击后产生的力，其持续时间极短，试验中难以被观测，计算时一般被忽略。第二项为流体在弯管处的摩擦力，数值较小也常被忽略不计。第三项为段塞上下游的压差，即段塞的驱动力。第四项为由瞬时冲击速度对壁面产生的作用力。

最近，Hou等[12]基于控制体理论，基于弯管内侧发生的流动分离现象，提出了一种新模型，冲击力的幅值与变化趋势与试验结果基本一致，其在x方向的冲击力表达式为

(4)

式中：Pe为上下游的压差；Cc为弯管处的流体收缩系数；Ke为水头损失系数。

综上所述，目前普遍认可的段塞流对弯管冲击力的简化计算公式为

(5)

等式右边两项分别为段塞受到的驱动力以及动量转换产生的冲击力。

2 试验装置及数值模拟

为了尽可能模拟实际工况，Bozkus等[13]借鉴了以往研究者[4-6]的试验装置，进行了更大尺度管径(10 cm)的试验。阀门下游主管道被设置成倾斜的，注水后可在弯肘处形成截留段塞，准确模拟了真实蒸汽管道中的截留段塞分布。相对于段塞的运动距离，段塞长度被设计得更长(超过其运动距离的五分之一)，以避免其在还未到达弯头时就已经破碎。与以前研究结果相比，压力测量系统的时间响应表现良好，动态压力测量显示了相似趋势。试验得到了弯头处的冲击压力时程曲线。

2.1 试验装置

文献[13]中的试验装置如图1所示，该装置包括位于上游容积为0.5 m3的圆柱形储气罐、一个DN100的球阀，一段内径为10 cm，长85 cm的垂直管段用于连接球阀，以及一根相对水平面呈4.6度，内径为10 cm、末端带有弯头的12 m长钢管。通过压缩机使储气罐充满压缩空气，以模拟发电厂管道中的压缩蒸汽。在试验过程中，仅控制初始段塞长度以及储气罐压力，当储气罐中空气温度及管道中水温达到环境温度时，对所有工况进行试验。当球阀快速打开时(开启时间约为16 ms)，上游的压缩气体将驱动段塞在管道中高速运动直至撞击到弯管处。位于弯管处的压力传感器记录了冲击压力的时程曲线，数据采样频率为1 000 Hz。

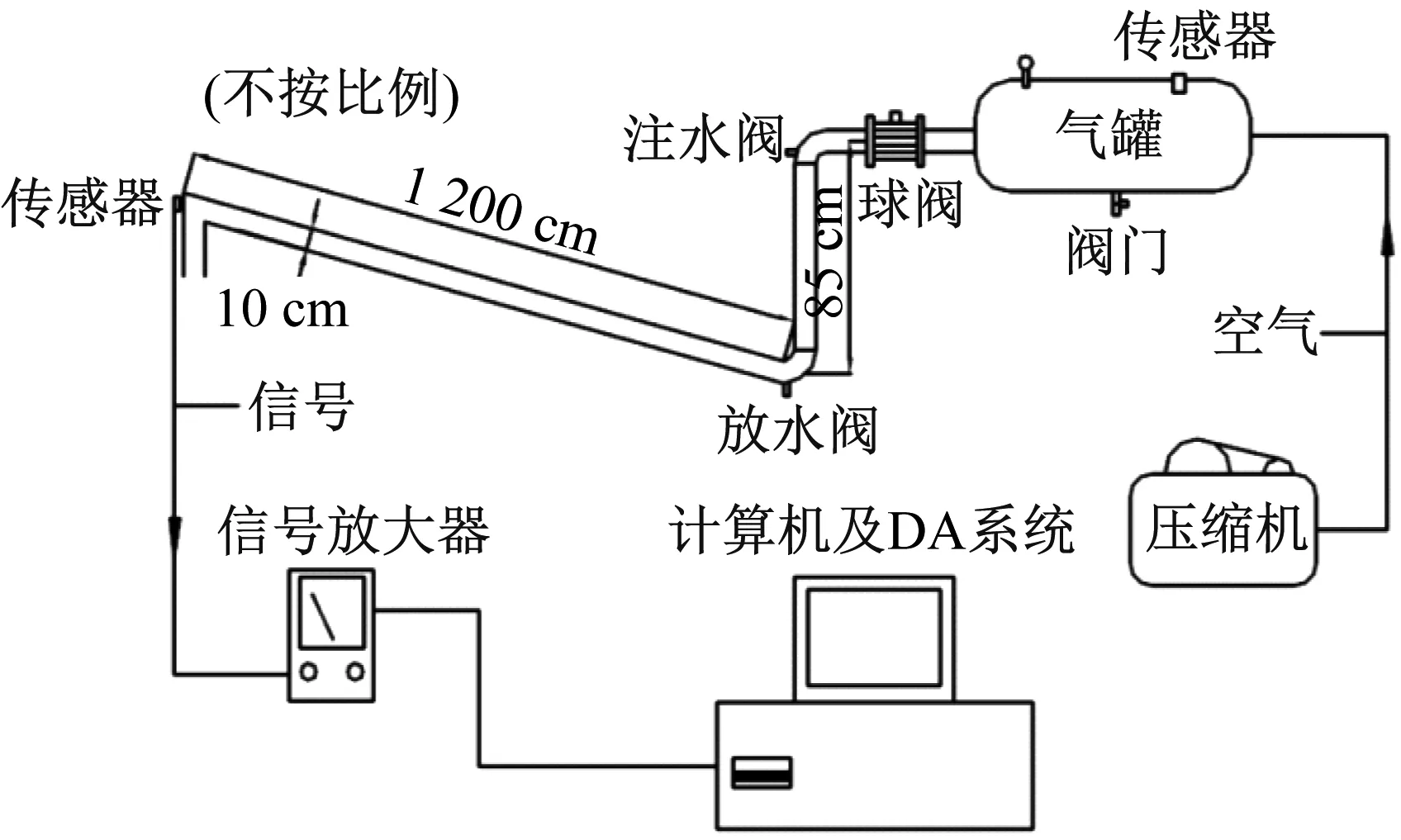
(a) 试验装置原理图

2.2 数学模型

针对段塞流问题，假设液体不可压缩，其连续性方程为

∇·V=0

(6)

动量方程为

(7)

假定气体与液体互不相容且彼此占据连续空间，因此变化的气液界面可以采用VOF模型予以描述。为真实还原段塞流在管道中的运动形态，提高模拟精度，本文采用RNGk-ε湍流模型。RNGk-ε模型的湍流动能方程和湍流动能耗散方程分别表述如下

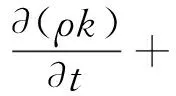
(8)

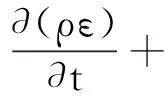
(9)

式中：k为湍流动能，表示速度波动的变化量；ε为湍流动能的耗散，表示速度波动对时间的耗散率；μ为运动黏度；μt为湍流黏度；αk=αε=1.39，Cε1=1.42，Cε2=1.68。

2.3 三维CFD模型

针对2.1中的试验工况，本节构建了一个三维CFD模型，运用有限体积法离散求解控制方程，压力与速度的耦合使用PISO算法，求解器采用Fluent 17.0版本。

前处理采用ICEM软件划分出O-grid型的结构化网格，这种网格容易实现流动区域的边界拟合，比非结构化网格更适用于管道中段塞流的模拟计算。同时进行了边界层网格划分，所得y+值主要分布在32～184。图2显示了管道整体及局部的网格划分图。

(a) 管道整体模型

由于管道倾斜将在段塞头部产生较长的自由液面，因此为了准确计算段塞初始长度，采用了如图3所示的方法，利用三角函数关系进行了简化。段塞长度L0为图中x、y的长度之和。

压力监测点设置在弯管中心轴线方向上。通过对驱动压力为5bar，段塞长度为3 m的算例进行试算，比较了80万～230万等7种不同网格数目的结果(见表1)，确定150万为合适的计算网格数。

图3 段塞标记方法(不按比例)

表1 网格数量无关性验证

将带边界层与无边界层的网格算例进行试算，比较了两组具有代表性的算例结果，如表2所示，结果发现无论是压力峰值还是峰值时刻，相对误差均在2%以内。这个误差相较于模拟误差是可以接受的，而计算耗时大约是3倍的关系，这将显著占用计算资源以及花费更长的无必要时间。因此综合考虑后，决定采用无边界层的网格进行了数值模拟。

表2 边界层网格无关性验证

针对之前部分学者提到的试验过程中气罐内压力的衰减情况[15]，本文考虑了恒定驱动压力以及随时间衰减的驱动压力两种情况。由于无法准确估计试验中气罐压力的衰减情况，根据以往经验[16]，假定压力为线性衰减且衰减率为30%，该步骤通过UDF完成。压力衰减的表达式为

Ps=P0(1-0.3ts/t0)

(10)

式中：Ps为衰减后的实时驱动压力；P0为初始驱动压力；ts为段塞的运动时间；t0为未考虑压力衰减情况下，段塞即将撞击到弯管处的时间，通过试算迭代得到。

由试验得到的时程曲线可知，达到压力峰值的冲击时间极短，为毫秒量级。因此，为了精确捕捉压力峰值，综合考虑试验数据以及试算结果后，确定时间步长为10-4s。试验中数据采样频率为1 000 Hz，为避免采样频率不同产生的影响，将上文提到的基于两种驱动压力情况计算得到的数据分别每隔10组取平均值，组成新的压力时程数据。

3 数值结果与分析

3.1 模拟结果验证分析

图4分别显示了L0=4 m，P0=2 bar工况下的段塞冲击弯管前后时刻的二维及三维云图，可以清晰地观察到段塞尾部气体对段塞内部的侵蚀以及段塞在弯管处的流动分离情况。同时发现段塞在冲击弯管前后，即使是在主体核心区，液柱与管道接触面附近仍然掺杂着大量气体。

表3对比了数值模拟结果与物理试验结果，其中L0表示段塞初始长度，P0表示段塞驱动压力，计算值表示每隔10组取平均值后的峰值压力；UDF计算值表示引入压力衰减后的峰值压力；UDF计算值取均值表示引入压力衰减后，再每隔10组取平均值后的峰值压力。表3中同时给出了各计算值与试验值的相对误差。对比分析表明，大部分数值模拟结果与试验结果具有良好的一致性，并且气罐压力衰减速率大小对模拟结果有较大影响。对于段塞冲击弯管的12个工况，采用恒定驱动压力模拟得到的压力峰值相较于试验值偏大。引入UDF模块进行气罐压力衰减设置后，结果更接近于试验值。另外，对计算数据取均值后，得到的预测值变小，这是因为压力峰值持续时间仅为两三个时间步长且衰减极快。

部分数值模拟结果与试验结果差异的原因主要有以下两个方面：

(1) 对于L0=6 m的工况，不考虑气罐压力减小时，计算所得压力值与试验值吻合较好，而设置压力衰减后模拟值变小。这是因为对于初始长段塞，气罐用于驱动其撞击到弯头处所需气体体积小，气罐压力衰减值远低于采用的30%压力衰减率。对于初始长度较短，驱动压力较大的情况，模拟得到的压力峰值相较于试验值偏大。例如，L0=4 m，P0=5bar工况下，不论经过何种处理，计算值依然偏大较多，主要是因为假定的气罐压力衰减不够大且不够快。当L0=5 m时，模拟值与试验值比较接近。

(2) 由于压力峰值持续时间极短，在压力传感器的数据采样频率为1 000 Hz的条件下，会存在某些持续时间极短的压力峰值捕捉不到的情况。而当数值模拟的时间步长为10-4s，即采样频率为10 000 Hz时，则避免了上述缺点，同时计算更易收敛。尤其是当段塞初始长度较短，而驱动压力较大时，此时段塞速度极快，峰值压力的衰减也更快，捕捉到的试验值均小于模拟值。而当段塞初始长度较长，驱动压力较小时，此时峰值压力的衰减相对慢一些，这也是在此情况下，试验值与数值模拟值基本吻合的原因。

(a) 冲击前

表3 CFD与试验压力峰值对比

对于3种不同初始长度液柱，数值模拟得到的压力时程曲线与文献结果对比如图5～图7所示。为与Bozkvs等提出压力时程曲线的单位保持一致，这里采用psi作为压强单位。结果表明，模拟所得整个冲击过程(幅值和时程变化趋势)与试验结果大致相同。同时，以L0=4 m为例，进行了频响分析，如图8所示，结果表明，监测点压力主频均位于0.5～2 Hz，压力幅值随着频率的增加而快速减小。P0=5 bar时，压力脉动的主频幅值最大，表明较大的驱动压力将会导致更剧烈的管道振动。

(a) 试验

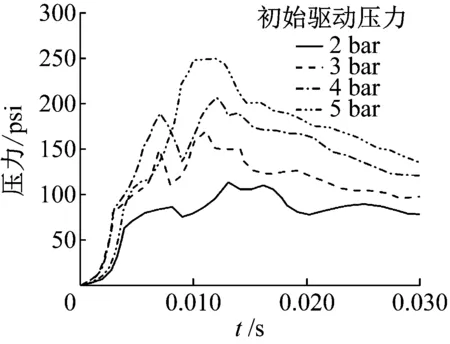
(a) 试验

(b) 数值模拟

3.2 段塞沿程质量脱落

段塞在管道中运动时，由于摩擦力及重力的存在，会发生质量脱落，导致段塞在冲击弯管前所具有的质量远小于其初始质量。为了进一步研究其质量脱落规律，定义段塞质量脱落率α=1-Ls(t)/L0，其中Ls(t)为运动段塞长度。

利用后处理软件CFD-POST，对Ls(t)进行了分析，并画出了质量脱落率随段塞运动距离的变化曲线(见图9)，其中横坐标代表段塞尾部距弯肘中心的长度。图示结果表明：对于本文所研究的工况，给定初始液柱长度时，段塞质量脱落率与其运动距离成正比，其曲线拟合的函数关系为：y=0.033x+0.113,R2=0.996。脱落率与驱动压力P0基本无关，即同样初始长度的段塞，不论其后方的驱动压力是多少，最终到达弯头时的液柱质量都是定值。

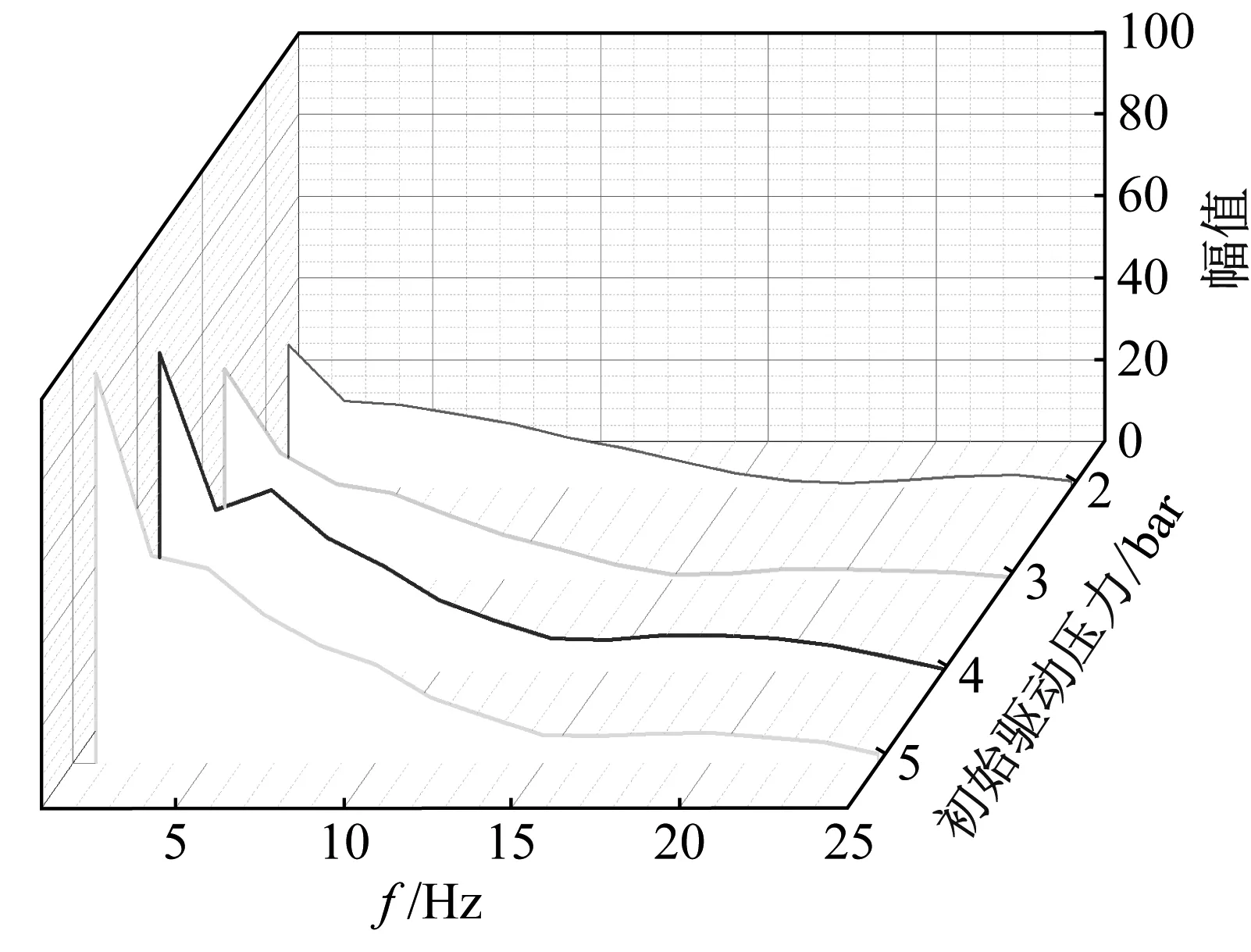
图8 L0=4 m工况下段塞冲击弯管压力频响曲线

图9 L0 =6 m的沿程脱落率曲线

段塞到达弯管处的脱落率与初始长度的关系如图10所示。显然，对于初始长度越短的段塞，因运动距离长，其到达末端弯管处的质量脱落率越大，但该脱落率与段塞初始长度并非线性关系，而是二次曲线关系，拟合曲线的函数关系为：y=0.012 9x2-0.276x+1.584,R2=0.997。对于短的段塞，质量脱落占整体段塞的比例接近90%，导致段塞在撞击时被加速到极高的速度，这是其峰值力较大的根本原因。

图10 不同初始段塞长度的脱落率曲线

3.3 弯管处段塞冲击模式

如前文所述，弯管处的冲击压力值与段塞冲击速度呈正相关。为了准确估计段塞对末端弯管的冲击作用，本文通过进一步的数值模拟，分析了段塞对弯管的冲击模式。对于2 bar驱动压力下，不同初始长度的段塞，结果显示冲击压力的变化趋势存在三种情况：

(1) 压力递减(L0=4 m)，如图11所示。段塞到达弯管时具有极高的速度，导致壁面对段塞的反作用力远远大于驱动力，加速度方向改变。速度峰值和压力峰值都出现在初始时刻。本文前述模拟的工况，都属于该冲击模式。

图11 L0= 4 m弯管处的压力时程图

(2) 压力递增(L0= 11 m)，如图12所示。段塞到达弯管的速度较低，反作用力小于驱动力，且随着液体由出口处不断流出，其速度持续增加。虽然弯头处的壁面反力增加，但段塞的加速度方向不发生改变。因此，速度和压力峰值都出现在冲击过程的末尾时刻。此外，在冲击过程中，因部分气体截留在弯头处，随着气团被逐渐冲刷释放，产生了小幅压力振荡(见图12)。

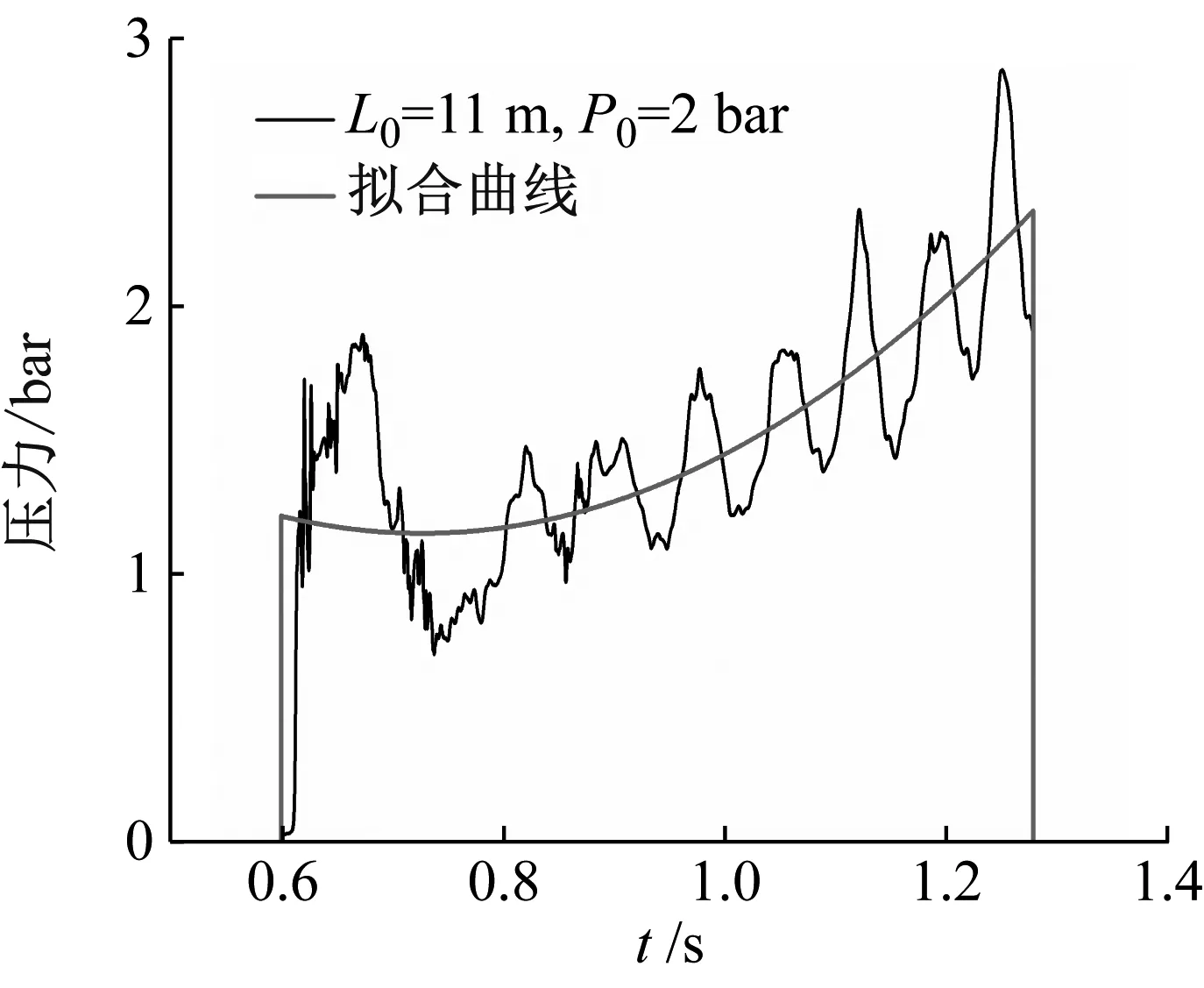
图12 L0=11 m弯管处的压力时程图

(3) 压力振荡(L0= 7.5 m)，如图13所示。段塞对弯管冲击后，壁面反力与驱动力基本相当。此外，与第二类模式类似，因弯管处截留气团的冲刷释放，冲击压力产生了大幅振荡。

图13 L0=7.5 m弯管处的压力时程图

对于2～20 bar之间的其他五种驱动压力，所得冲击模式跟2 bar条件下的模式基本相同。这三种冲击模式可通过公式(5)予以进一步阐释。当段塞运动到弯管时，因方向改变，在弯管处产生冲击压力，其大小取决于段塞的冲击速度。当段塞运动到弯头时的速度较大时，因速度引起的壁面反力远大于段塞驱动力，段塞具有反向加速度，所以速度逐渐降低，冲击压力降低。当段塞运动到弯头时的速度较小时，因速度引起的壁面反力小于段塞驱动力，段塞加速度方向不发生改变，速度继续增加，冲击压力增加。当段塞运动到弯头时的速度适中时，因速度引起的壁面反力与段塞驱动力相当，段塞加速度为零，所以速度和冲击压力基本不变。

对于实际工程应用而言，我们主要关注的是第一种冲击模式，即压力峰值出现在冲击的初始时刻，此时段塞对管端结构的冲击载荷大，破坏力强，这是应该避免的。

3.4 压力峰值计算方法验证

为了探究高速运动段塞对弯管冲击压力的计算方法，提取了12个工况下的段塞冲击速度，并依据式(5)进行了数值计算，计算结果如表4所示，表中的Pe值为压力衰减30%后的驱动压力。表4中同时给出了理论计算值与试验值及数值模拟值之间的相对误差。整体来看，理论计算结果与数值模拟结果相吻合。由于段塞的瞬时速度值是通过等距离构造管道截面，再取截面的平均速度所得到的，考虑到其误差，因此可以认为通过该方法能够相对准确地计算瞬时冲击压力。

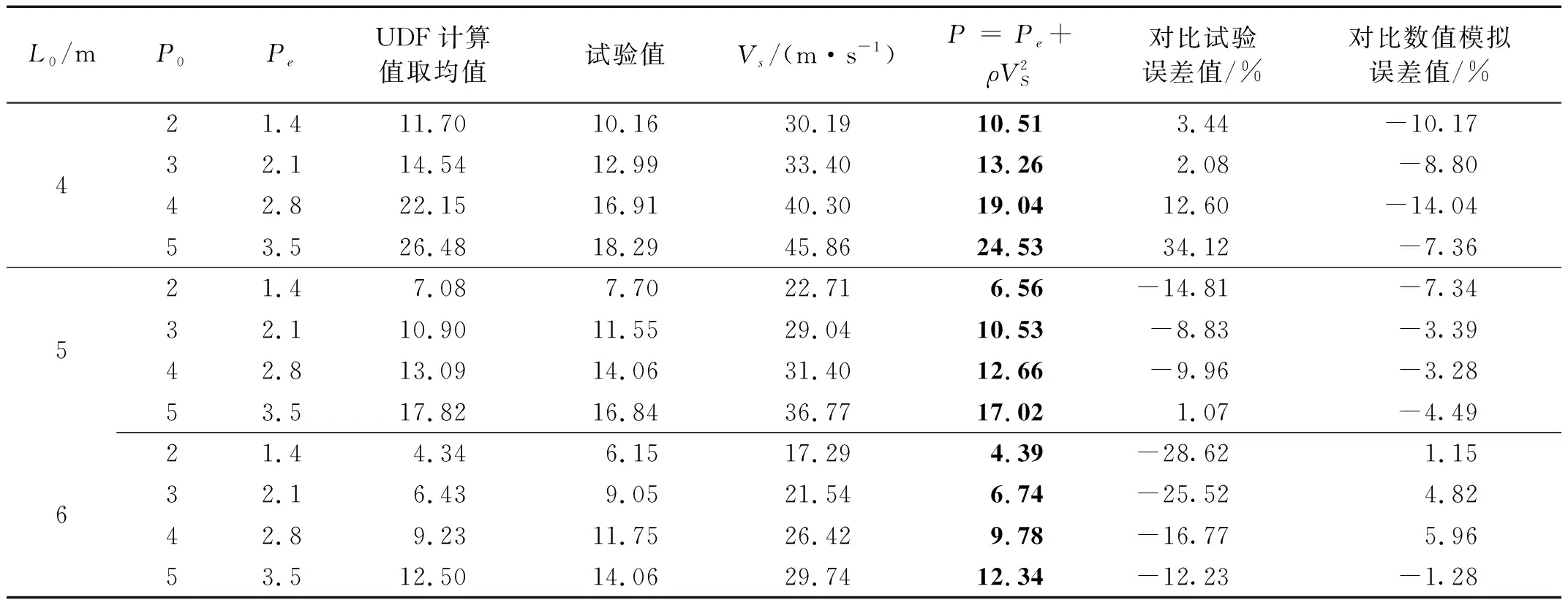
表4 数值计算的压力峰值

4 结 论

本文针对单个段塞在空管里的运动及其对管端弯头的高速冲击问题，在总结分析以往理论与试验研究的基础上，结合已有试验数据，建立了段塞流瞬态冲击三维数值模型，并利用该模型模拟了文献中不同工况下段塞的运动及其对弯管的冲击过程，得到了相应的冲击压力时程曲线。对于不同初始长度段塞，采用合适的压力衰减率，数值模拟结果具有较高的准确度，冲击压力时程曲线与试验结果基本吻合。在此基础上，通过数值试验，分析了段塞运动过程中的质量脱落率，提出了段塞对弯管的3种冲击模式，以及段塞对弯管冲击压力的简化计算公式。所得主要结论包括：

(1) 对于初始长度给定的段塞，在驱动压力主导时，运动单位距离时的质量脱落率相同，最终到达弯头时的液体质量为定值。

(2) 段塞冲击过程中弯管处的压力变化有三种模式：(i) 压力峰值出现在冲击初始时刻，然后快速减小；(ii) 压力突增后，随速度的增大，压力增大，峰值出现在冲击末尾时刻；(iii) 压力突增后，在该值附近上下波动。

(3) 对于单个运动段塞对弯管的瞬态冲击压力，简化计算公式(5)能够准确地计算冲击压力峰值，理论计算值与试验及数值模拟结果基本吻合，该计算方法在实际工程应用上具有指导意义。