低信噪比条件下深度学习麦克风阵列波束形成

2022-12-14钟双莲刘雨佶章宇栋陈东升

兵器装备工程学报 2022年11期

钟双莲,童峰，3，刘雨佶，章宇栋，陈东升，3

(1.厦门大学水声通信与海洋信息技术教育部重点实验室，福建厦门 361005；2.厦门大学海洋与地球学院，福建厦门 361102； 3.厦门大学深圳研究院，广东深圳 518000)

1 引言

随着智能家居、远程会议、智能装备、可穿戴设备技术蓬勃发展，作为语音入口的语音交互技术发展迅速，麦克风阵列在前端语音增强中得到广泛研究和应用[1-4]。与单通道语音增强算法相比，麦克风阵列语音增强算法可以充分利用多通道语音空间信息实现噪声、干扰抑制。但是，在低信噪比环境下，传统麦阵增强技术面临增强效果下降、语音清晰度和可懂度降低等问题，严重影响正常工作。

麦克风阵列波束形成算法主要有3类：固定波束形成算法(基于时延累加波束形成(delay-and-sum beamforming,DSB)算法[5]、滤波累加波束形成(filter-and-sum beamforming,FSB)算法[6])，自适应波束形成算法[7]，后置滤波算法[8]。固定波束形成算法在设计滤波器系数时通常是根据一定的准则，利用已知声源位置、麦克风阵列阵型、声源场景等先验知识来设计，适用于固定的场景，以及非相关的噪声环境，但是对相关的噪声以及动态声学场景效果较差。而自适应波束形成算法通常是利用输入信号的统计特性来计算滤波器系数，从而能适应动态的声学场景，但是波束形成的收敛速度比较慢，难以跟踪快速变化的声学场景。后置滤波算法主要是解决非相干噪声场中不相关噪声信号，但是现实多是相干噪声环境[9]。

基于深度学习神经网络模型的麦克风阵列语音增强算法成为了新的研究热点。在时频掩蔽多通道波束形成中，结合深度学习得到广泛研究，邓贺元等[10]通过联合频谱特征和空间特征进行多通道的波束形成语音增强，在测试数据集上下降了27.6%的WER。因时频掩蔽方法需要利用语音和噪声的频谱、相位特征的区分信息，在低信噪比条件下语音、噪声频谱信息往往难以明显区分，导致增强效果下降[11]。

面向语音识别需求，采用前端、识别端联合序列训练[12-13]。Ravanelli等[14]提取梅尔倒谱系数(mel-frequency cepstral coefficient,MFCC)特征，并改进深度神经网络结构来增加波束形成的语音增强网络和语音识别网络的通信，通过联合训练来降低低信噪比条件下的语音识别词错误率(word error rate,WER)。这类优化方式可以直接服务于提高语音识别准确率的任务，但是因无需对语音信号进行重构，不输出增强的语音信号，因而不适合需要语音输出的应用，如远程会议、通话终端等。

考虑到智能语音应用中低信噪比场景，引入深度学习进行麦克风阵列波束形成语音增强，本文通过构建一个空间域优化的深度学习波束形成网络，获得增强语音输出，从而保证低信噪比条件下的语音增强性能。介绍了波束形成网络框架设计及基于LSTM波束形成网络结构，最后对所提方案进行仿真和实验验证。

2 基于深度学习的波束形成网络设计

2.1 网络结构框架

本文所提深度学习波束形成网络框架如图1所示，网络分为波束形成器训练部分和语音增强部分(又为测试部分)。模型训练阶段，首先对训练集的多通道语音信号进行预处理，接着输入神经网络中，以干净的单通道信号的特征值为训练目标进行训练，训练完成后，对测试集的多通道语音进行同样的预处理方式后，输入到训练好的波束形成器网络和语音重构得到增强的语音信号。

其中预处理模块包括时频分解和特征提取。时频分解方法主要有短时傅里叶变换法(short time fourier transform,STFT)和小波变换等2种。本文中的网络模型采用STFT对多通道语音信号进行时频变换，得到频谱X。STFT的帧长是512个采样点，帧移是帧长的一半，故X的维度为257F，F为帧数;选取z-score[15]标准化后|X|的功率谱作为特征。

图1 网络结构框图

2.2 波束形成的神经网络模型

当前基于深度学习的神经网络模型较多，其中传统的深度神经网络(deep neural networks,DNN)模型存在对时序信号处理不敏感和参数膨胀的问题；而深度循环递归神经网络(recurrent neural networks,RNN)模型能对语音信号按时间序列进行分析[16]，但是存在梯度消失的问题；而LSTM神经网络模型不仅适合对于时序信号的处理，而且从当前的研究表明，相教于传统的DNN神经网络模型,其对于未出现的说话人和噪声具有更好的泛化性[17]，同时也解决了RNN神经网络模型梯度消失的问题。因此在Tensorflow框架上搭建了基于LSTM的神经网络模型。

神经网络结构主要有2层LSTM(128 维)的主网络、1层DNN 掩码(257×6 维)的掩码(MASK)模块和1层遮蔽层的叠加输出模块，模型主体网络结构框图如图2。其中多通道的特征通过LSTM层训练，输入到一个DNN MASK层，获得每个通道的MASK估计结果，为了与输入特征维度适配，MASK层的节点数为F(通道数)。DNN MASK层输出结果再与输入多通道特征值相乘做加权平均后得到预测的单通道的特征。

图2 模型主体网络结构框图

2.3 损失函数与训练目标设置

损失函数为训练目标和预测输出的欧式距离，并采用Adam优化器作为网络的优化器。网络训练目标为幅值控制的单通道功率谱特征值。幅值控制根据本文中所训练的波束形成网络的波束图能量分布设计，其中波束形成网络对准方向相应通道信号的幅值无损失，其他通道信号根据与波束形成网络对准方向的角度差来对该信号进行幅值控制。θmodel为模型训练所对准的角度，θsignal为该通道信号的方向，Atarget为幅值控制后的通道信号的幅值，Asignal为原始通道信号的幅值，通过幅值控制，使得模型训练的波束具有指向性。训练目标幅值控制权重设置如表1所示。

表1 训练目标幅值控制权重设置

3 实验设置与实验结果

3.1 数据库说明

模型训练数据集采用中文语音数据库THCHS-30数据库[16]，该数据集是在安静办公室环境下录制的单通道语音信号，信号的采样率16 kHz,数据库总时长约为30 h，该数据包含了训练集、验证集和测试集。将数据库的训练集单通道语音信号作为仿真多通道数据的原始信号，仿真均匀分布的麦克风圆形阵列的时延关系并生成多通道语音信号，其中麦克风阵列直径为65 mm，获取以15°为划分的24个角度的多通道语音信号。具体的仿真条件为：先通过IMAGE模型[18]模拟11 m×11 m×3 m典型办公室尺寸的房间冲激响应，产生反射强度分别为0.2、0.4、0.6、0.8的房间冲激响应,将房间冲激响应与多通道语音信号进行卷积，得到4种不同混响强度的混响信号,再随机叠加信噪比为5 dB、10 dB、15 dB的白噪，来仿真实际环境中的带噪语音。

仿真测试集在不同信噪比(signal to noise ratio,SNR)下带噪语音的改善效果如表2所示，本文中的SNR[19]计算公式为：

(1)

式(1)中：Psignal为信号的功率；Pnoise为噪声的功率。

表2 传统算法及神经网络模型SNR结果

从表2可以看出，波束对准角度的语音信号经过FSB算法处理，信噪比平均能提升7 dB左右，这是由于仿真测试集叠加的是高斯白噪声，符合FSB算法的算法模型，处理效果好，总体上看，本文算法的处理效果略好于FSB算法。

3.2 实验设置与结果分析

3.2.1实验设置

麦阵增强实验在某大厅中进行，实验环境如表3所示。实验中利用 MARSHALL Kilburn移动式蓝牙音箱播放文献[4]中的数据库语音，利用ReSpeaker Far-field Mic Array 7元(圆周均匀分布6个、阵中心分布1个)麦克风圆形阵列作为采集设备进行麦阵信号转录。转录过程中以麦克风阵列为中点调整对准音响的角度，每次调整30°，总计获得3 549条有效转录麦克风阵列语音数据。为了模拟低信噪比环境的典型噪声，对转录麦克风阵列语音数据随机叠加实录吹风机、音乐、道路背景噪声，生成不同信噪比的带噪信号进行测试。

表3 实验环境规格

3.2.2实验结果分析

实验选取SNR以及词错误率(word error rate,WER)来评估模型的性能。图3展示了FSB算法、LSTM波束形成算法处理的增强后语音的波形图。由图3可以看出：波束对准角度的语音信号经过FSB算法增强后，频域有一定的增强效果，信号高频部分的噪声被抑制，噪声能量小，但同时信号部分的中高频分量也有一定的减弱,而对于低频部分1 K以下的噪声抑制不明显，甚至略有增强；而经过本文算法增强后，语音信号时域的噪声段信号幅值很小，时域的增强效果明显，并且频域方面，在高频抑制噪声干扰的同时对高频分量的增强最明显，信号失真最小。

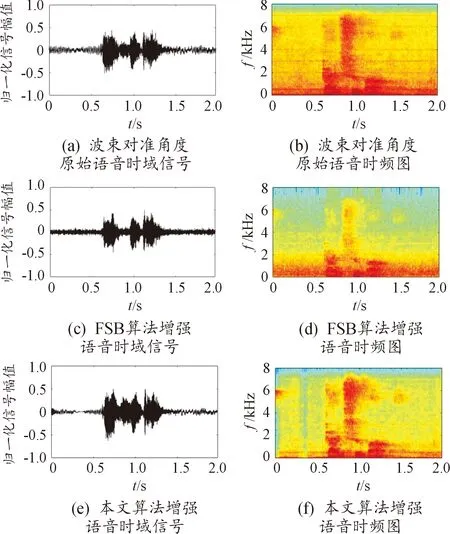
图3 波束对准角度的语音信号波形图和时域图

具体对比在不同指标下模型的提升效果，将不同信噪比的实验信号经过FSB波束形成算法、LSTM波束形成算法处理增强后，其语音的平均信噪比结果如表4所示。

表4 传统算法及神经网络模型平均信噪比SNR结果

从表4可以看出，在实际测试场景中，传统FSB算法对于原始信号没有信噪比提升的效果，这是由于FSB算法虽然对于高频成分的噪声的抑制比较强，但是对于低频的噪声抑制比较弱,甚至可能有加强噪声的趋势，而实际场景噪声的能量由低频成分噪声占大部分；本文算法在信噪比较高的环境中，信噪比提升与传统方法相当；但在低信噪比情况下，本文算法对语音的增强效果明显优于传统方法。

进一步使用语音识别软件[20]对实验增强语音进行识别性能评估，文本识别率定义为：

R=1-RWE

(2)

式(2)中，RWE为文本的词错误率。

在波束对准角度的信号经过FSB算法、本文算法处理后的信号识别率对比,表5给出了实际办公室场景下的对应结果。由表5可以看出，在不同信噪比情况下，本文算法都较FSB算法有更高的识别率，平均提高在5%左右，这是由于本文算法在降低环境噪声的同时保留了较高的高频成分的信号，使得信号的失真较少，使得信号的识别率较高。需要指出，实验采用识别率主要用于从识别端角度评估不同语音增强方法的性能，实际上,此时的识别率并不具有人机交互实用意义。

表5 传统算法及神经网络模型识别率计算结果

最后对比传统FSB算法和本文算法的算法复杂度，如表6所示，基于LSTM深度学习模型的算法，在增强阶段算法复杂度为O(LSTM),其计算公式为[21]：

O(ni*n1+4nl*nl+3nl+nl*no)

(3)

式(3)中：ni为输入层的单元个数；nl为隐藏层的单元个数；no为输出层的单元个数。

由此可知，LSTM深度学习模型的算法复杂度与模型的层数和单元个数有关；而传统算法FSB算法复杂度与波束形成器的滤波器的阶数以及信号的通道数有关O(FSB),其为：

O(N*FIR1)

(4)

式(4)中：FIR1为滤波器的阶数；N为通道数。训练阶段LSTM网络层的算法复杂度为:

T*S*O(LSTM)

(5)

式(5)中：T为训练次数；S为数据量。计算LSTM深度学习模型的参数量为1.7 M个；通过使用8GB RAM和3.00 GHz Interl(R)Core(TM)i5-7400CPU处理器，计算增强阶段100条时长为1 s的语音信号的平均运行时间，其中FSB算法的运行时长为0.072 s，而基于LSTM深度学习模型的运行时间为0.062 s，在增强阶段，基于LSTM深度学习算法较传统算法的运行速度有所提升。传统算法及神经网络模型算法复杂度对比如表6所示。