高速列车车厢内部爆炸冲击波传播规律及载荷特性研究
2022-12-14姚术健马一先叶逸之冯兴民孙成名史湘石
姚术健,马一先,叶逸之,冯兴民,孙成名,史湘石
(1.中南大学 交通运输工程学院, 长沙 410075;2.中南大学 轨道交通安全教育部重点实验室, 长沙 410075;3.中南大学 轨道交通安全关键技术国际合作联合实验室, 长沙 410075;4.福州市江阴工业区开发建设有限公司, 福州 350309; 5.陆军特种作战学院特种技术系, 广西 桂林 541000)
1 引言
根据2016年修订的《中长期铁路网规划》,预计2025年我国铁路运营里程达到17.5万公里。作为我国经济的重要支柱,铁路不仅是我国重要交通方式,还是关系到民生的重点工程。随着我国铁路网的不断完善,高铁列车的开行对数也在迅猛增长,与此同时,列车安全运行的压力也不断增加。由于列车空间较为封闭且内部构造较复杂,一旦发生内部爆炸等恶性事件,短时间内难以迅速开展处置及救援工作[1-3]。
针对封闭空间的内部爆炸问题,国内外许多学者展开了相应研究。主要集中在封闭空间内影响爆炸的相关因素及空间结构的载荷分布特性上。Hu[4]、谭波等[5]研究了封闭空间的内部爆炸载荷分布。Rousseau P[6]、罗小丽等[7]通过有限元分析研究了不同环境下影响爆炸的因素,分析环境属性对封闭结构爆炸响应的影响。谷鸿平等[8]分析了典型箱体结构内爆冲击波传播特性,并对Hopkinson爆炸相似律在结构内爆条件下的适用性进行了研究。在运载工具的动态响应方面,Larcher[9]、欧阳作林[10]基于流固耦合计算研究了列车内部爆炸产生的冲击波造成的影响以及人员的伤亡风险。Edri等[11]基于单室结构内TNT封闭爆炸实验,研究了峰值压力随时间衰减的变化规律。张文岚等[12]研究了不同爆距下车窗玻璃板心的响应指标,认为板心的位移、速度与加速度峰值随着爆距增大呈指数型函数衰减。但已有研究主要集中在运载工具乘客和内容物受冲击波损伤特性及爆炸冲击波传播规律上,对高速列车车厢结构内部爆炸冲击波传播规律及车体受损特性的研究相对不足。
爆炸冲击波因传播速度快、破坏性大,试验测试十分困难,本文研究基于有限元程序ANSYS/LSDYNA建立有窗车厢和无窗车厢模型,分析不同当量炸药爆炸车厢内流场特性及对车厢结构所产生的破坏效果。分析结果对于爆炸作用下车厢毁伤效果评估、车厢防爆结构设计具有一定的参考价值。
2 计算模型及工况
2.1 材料模型
计算模型中空气被视为没有粘性的理想流体,密度为1.293 kg/m3,在ANSYS/LSDYNA中利用关键词Mat_Null定义。理想气体的状态方程通过线性多项式状态方程*EoS_Linear_Polynomial定义[13]:
P=c0+c1V+c2V2+c3V3+(c4+c5+c6V2)E0
(1)
式中:E0为初始能量;V=ρ/ρ0-1;ci为不同系数,其中c4=c5=γ-1;γ为比热的多向比;压力由式(2)给出:
(2)
式中:ρ/ρ0是当前密度与参考密度的比值。在标准大气压下γ=1.4,E0=2.5×105J/kg。炸药爆炸过程模型采取CJ模型。CJ模型通过起爆点、爆炸速度确定模型中各节点起爆时间。
在有限元分析中,采取CJ模型需要与之相适应的状态方程,本文中用在数值模拟领域应用较为广泛的JWL状态方程,其等熵方程形式如下[14]:
(3)
式中:P为爆轰压力,Pa;V=v/v0为相对体积;v为比容;v0为初始比容;E为单位体积内能,J/m3;A、B、R1、R2、ω均为材料常数。
在我们前面的研究中[8],利用试验结果对结构内部爆炸数值仿真模型进行了校核与验证,如图1所示为箱内爆炸压力试验曲线与仿真曲线结果[8]。图2所示为内爆作用下钢箱结构损伤特性试验与仿真结果[15]。研究结果表明本文中所用计算模型合理。

图2 内爆作用下钢箱结构损伤特性试验与仿真结果图Fig.2 Test and simulation comparison of damage characteristics of steel box structure under implosion
2.2 有限元模型
本文中研究车厢为CRH1型动车组列车的头车,车厢尺寸为2 695 cm×333 cm×404 cm。本文中对模型进行了简化并忽略冲击波引起车体的变形和破坏。针对无窗货运车厢及有窗客运车厢分别建模,如图3所示,有窗车厢侧壁车窗从前到后分别为1号到5号。网格采用四边形网格,每个网格大小为8 cm。

图3 列车车厢模型示意图
空气域尺寸为2 705 cm×345 cm×415 cm,单元类型为SOLID164,边界面皆采用边界关键字*Non_Reflection定义为无反射边界以消除外部反射波的影响[16]。炸药选用高能燃烧模型(High_Explosive_Burn),密度为1 610 kg/m3,通过关键字*Mat_High_Explosive_Burn设置为球状,并通过关键字*Initial_Volume_Fraction_Geometry填充进空气域网格。为提高计算精度,炸药附近网格较密,网格尺寸为2 cm。车厢结构模型与空气域模型之间采用流固耦合算法。将车体内空气视做理想气体,爆炸冲击波在车体内传播过程视为绝热过程。空气域模型截面图如图4所示。

图4 空气网格模型示意图
2.3 计算工况
交通恐怖爆炸袭击主要为炸弹爆炸或自杀性人体炸弹爆炸,本文中计算炸药当量分别设置为6.7 kg、23 kg、54 kg,炸药位置设置在车体中心,结合车体有窗无窗,共计6个工况,见表1。

表1 计算工况Table 1 Calculation conditions
3 爆炸冲击波在车厢内传播规律分析
3.1 无窗车厢内传播规律
本节以表1工况1为例,分析无窗车厢模型中冲击波状态云图。图5为不同时刻起爆点所在横截面上冲击波的传播过程:
① 炸药起爆后,冲击波在未接触壁面时能够视为自由场爆炸模型(图5(a)所示),产生球面冲击波向外扩散,压力逐渐降低;② 经过约0.6 ms,冲击波首先到达侧面车体并发生反射(如图5(b)),随后冲击波到达车顶与车底开始产生反射并向角隅处传播(如图5(c)),反射产生的冲击波在角隅处聚集叠加(如图5(d)),此处压力达到最大9.07 MPa;③ 由各个角隅处冲击波反射回到车体中央再次叠加(如图5(e));此后冲击波在角隅与车体中央间不断重复上述过程,能量逐渐降低。
冲击波在无窗车厢内纵截面上传播过程如图6所示。图6(a)~(d)与图5中不同时刻相互对应,不再描述。因车厢前端车体收缩[图6(f)],冲击波在上壁区域压力(1.44 MPa)明显大于同一截面车底处压力(0.786 MPa)。随后,冲击波在车体前端发生反射向车底叠加[图6(f)],车底处压力经叠加达到3.96 MPa。

图6 不同时刻的纵截面冲击波状态图
3.2 有窗车厢内传播规律
以表1工况4为例,分析有窗车厢内冲击波传播规律。有窗车厢内爆炸冲击波横截面传播规律与无窗车厢大致一致。但受车窗影响,冲击波在侧壁大量逸出[如图7(a)、(b)],从侧面可以观察到车窗处不断有冲击波传出[如图7(c)、(d)],导致车窗处压力峰值明显低于无窗情形。图8给出了沿车身排列的车窗处压力峰值,沿冲击波传播路径,车窗处压力峰值逐渐降低,距爆炸点相同距离的车窗处压力曲线变化趋势基本一致。
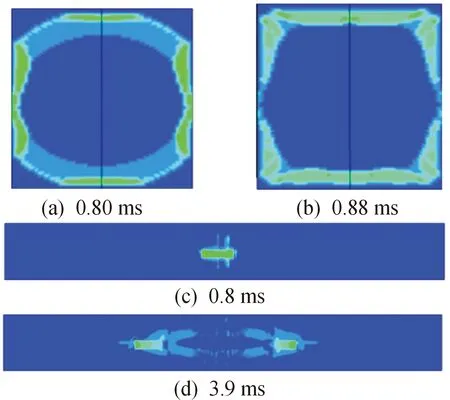
图7 有窗车厢冲击波逸出示意图
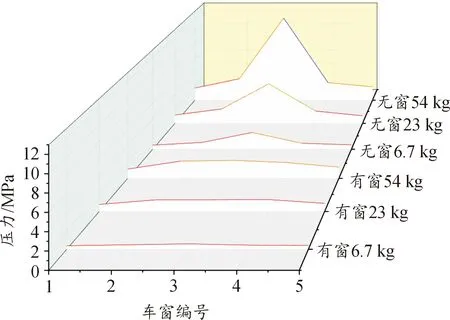
图8 不同车厢不同位置车窗处压力时程曲线
3.3 车厢内壁爆炸载荷特性分析
以炸药当量23 kg、无窗模型为例,为了研究冲击波在车厢壁面压力的变化情况,取车厢内不同位置的多个点进行分析。采样点位置如图9所示,O点为炸药位置,位于车厢中央,A、B、C位于车体表面,D、E、F、G位于车厢后壁,L、M、N、L位于车头弧线,H、I、J、K位于车体轴线并分别距爆炸点3 m、6 m、9 m、12 m。
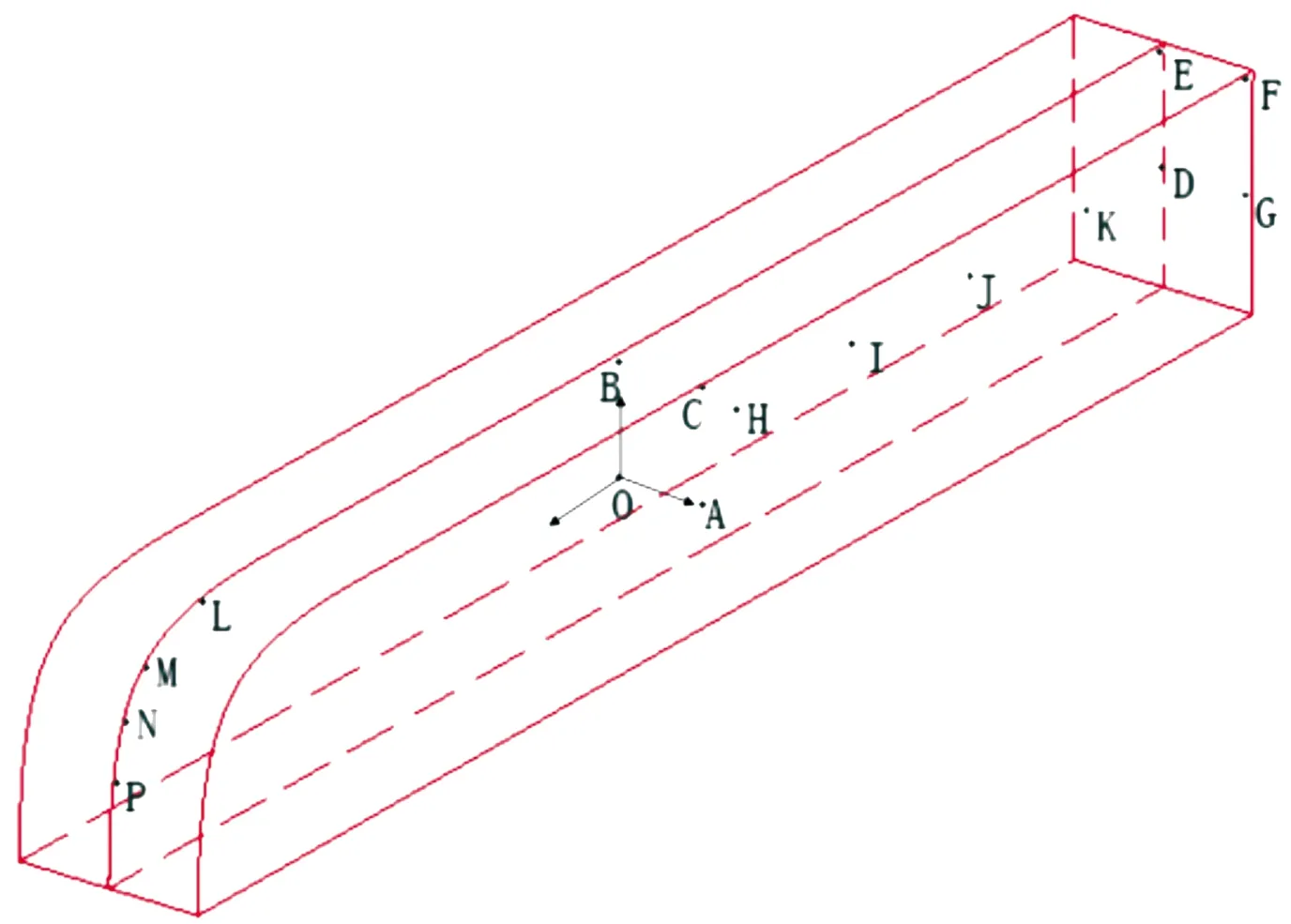
图9 车厢内采样点位置示意图
图10为爆炸横截面上典型位置压力曲线。炸药在O点爆炸后,冲击波率先传到A点,因距离爆炸中心较近,A点压力略大于B点。随后冲击波经过反射在角隅处C点叠加,使得此处压力急剧增大且显著高于车厢侧壁与车顶(如图10)。

图10 爆炸横截面上典型位置压力曲线
图11—图13为车厢内典型位置压力曲线。在车尾部分,冲击波在传播过程中几乎同时抵达4个典型位置采样点,反应在应力云图为4个点基本在同一时间出现第一次超压峰值(图11),角隅处F点由于发生汇聚作用,压力峰值最大。4个采样点处冲击波均发生多次反射。

图11 车尾横截面上典型位置压力曲线
在车厢纵截面上,球面冲击波率先抵达H点,随后经反射叠加并向后传播(图12 (a)),在压力图像中反映为H点出现多次超压峰值,I点出现一次超压峰值。通过比较可以看出,爆炸冲击波在车厢内部将数次反射,图12(b)显示参考点均出现多个压力峰值。距车尾更近的参考点压力峰值更多,时间间隔更短。同时,冲击波在车厢中传播时,随着离爆炸中心距离的增加,超压峰值可能由于反射而增大。L、M、N、P点位于车头部分顺序排列,爆炸冲击波向车头传递,受车头收缩影响,超压沿车头弧线显著提高(如图13)。
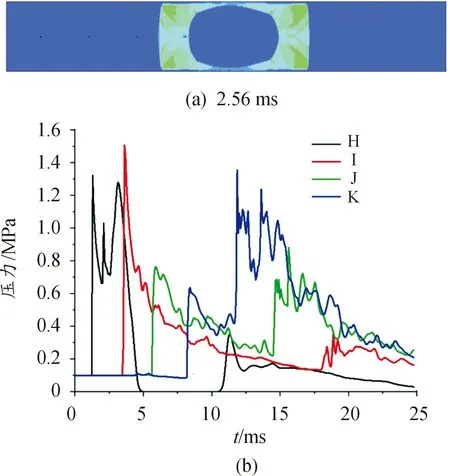
图12 车厢纵线上典型位置压力曲线
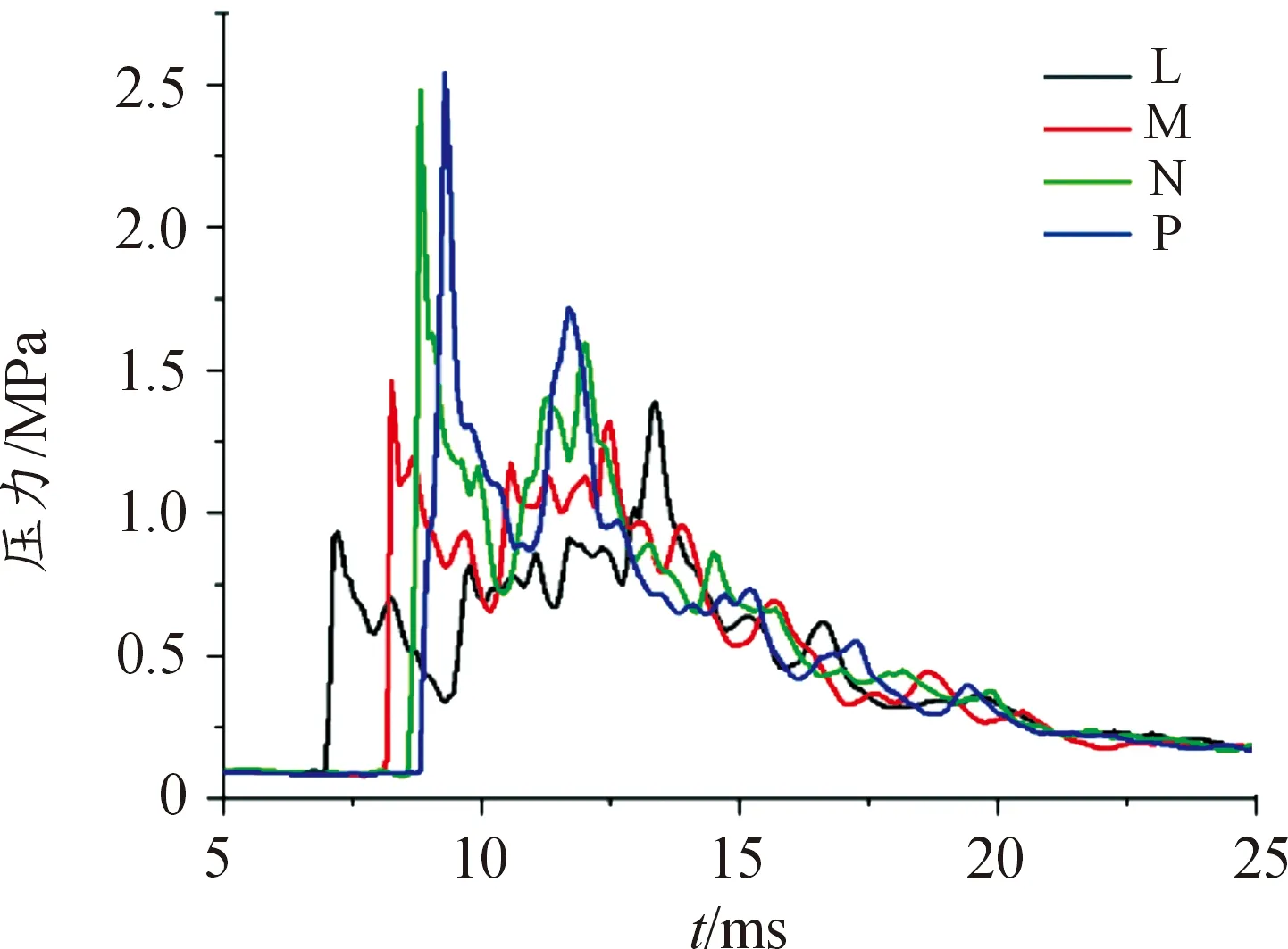
图13 车头典型位置压力曲线
图14为车体内典型位置的冲量曲线,可知不同位置的典型点冲量曲线差异较大。A点所受冲量较小,而C点由于冲击波在此反射叠加,冲量明显高于A、B两点。D、E、F、G点受平面波影响,压力曲线上升趋势大致相同。H点距爆炸中心较近,故冲量较早增加,但一段时间后增速放缓。另外,车体结构相对复杂的位置冲量将高于附近区域(如图14C、F曲线)。

图14 车体内典型位置冲量曲线
图15为有窗车厢内典型位置压力。与无窗车厢内冲击波传播规律基本类似,但由于有窗车厢存在泄压,压力峰值普遍比无窗车厢要小(如图10和图15(a))。同时因大量冲击波从车窗逸出,超压在车体内部叠加次数较少,车体内压力波峰数较无窗车厢偏少(如图12(b)和图15(b)),靠近车尾的参考点处压力较大(图15(b))。

图15 有窗车厢内典型位置压力曲线
图16显示了车体底面的压力最大值分布。车体为左右对称结构,因此中轴线左右压力分布状况相同。显然压力最大值分布除受距爆炸点的空间距离影响外,还受压力采样点处结构复杂度的影响。在爆炸中心横截面上,底面采样点压力先下降后急剧上升,在角隅处达到最大值,此处承受压力为底面最大。在纵向截面中,随着距爆炸中心距离的增加,压力呈下降趋势。车头部分压力分布与车尾状况不同,由于车头部分结构不完全规则,前端高度收缩导致冲击波发生多次反射,车头处底面压力先上升后下降,经过叠加后,压力达到3.96 MPa(图16)。

图16 无窗车厢底面压力最大值分布图
4 结论
本文中以有窗和无窗两种高速列车车厢结构为研究对象,对车厢内部爆炸的冲击波传播规律进行了数值仿真研究,结论如下:
1) 受车体结构影响,爆炸冲击波在车厢内部存在多次反射,部分区域多次受到冲击,反射冲击波容易在车厢角隅处汇集叠加产生较高压力。对于中心爆炸工况,冲击波在被反射回车体中心汇集后,将继续向四周传播。横截面的角隅处冲击波汇集叠加产生的超压最高,无窗车厢角隅处产生的叠加效应比有窗车厢更明显,23 kg当量下达到9.07 MPa;由于反射叠加效应,同一采样点的第一个超压峰值可能不是整个过程中的最大超压峰值;车头部分车底受力最大达到3.96 MPa。
2) 车厢内典型位置冲量大小与爆距关系较小,与该典型位置的车体结构关系较大,车体棱、角隅等复杂结构冲击波相互影响作用区域处冲量显著增大。
3) 有窗车厢受到的压力载荷远小于无窗车厢,说明对于抗爆设计,列车车厢应适当增设泄爆口。
