基于点云分割的移动机器人运动目标跟踪方法

2022-12-14谢国坤张培培王宁宁

兵器装备工程学报 2022年11期

谢国坤，张培培，王宁宁

(西安交通工程学院，西安 710300)

1 引言

近年来，随着智能机器人视觉跟踪领域的飞速发展，使得传统静态的目标跟踪方式，已无法满足需要，因而如何实现机器人运动目标跟踪一时间备受青睐[1]。一方面，当前较流行的机器人运动目标跟踪方法，虽在机器人领域取得了一定成果，但移动机器人运动在障碍物下的运动目标跟踪过程中存在一些问题。通常的目标跟踪算法都是基于像素的全局搜索，然而该方法计算量大，耗时满足不了移动机器人控制的实时性要求，并且其易受到背景中相似特征物体的干扰。

王立玲等[2]提出了基于改进Camshift算法的运动目标跟踪方法，但是该方法在有障碍物干扰时，NAO机器人运动目标跟踪精度下降。李欣等[3]提出了基于ECO-HC改进的运动目标跟踪方法，该方法虽然成功实现了机器人对运动目标的跟踪，但是存在误差偏移量较大、不稳定等问题。上述2种方法在跟踪目标时，易受背景中干扰因素的影响，导致运动目标跟踪精度下降[4-5]。

为了改变这种现状，本文提出基于点云分割的移动机器人运动目标跟踪方法，该方法以移动机器人为研究对象，对运动目标的坐标等点云数据进行采集和出力，降低了运动目标跟踪过程中的误差偏移量，提高了机器人在运动目标跟踪中的稳定性，更适应实际需求。

2 方法设计

2.1 点云数据采集与处理

2.1.1点云数据采集

考虑移动机器人采集图像中的目标存在随机性，因此，在采集点云数据过程中，为避免测量误差，采用非接触设备采集点云数据。具体采集过程为：

将非接触扫描设备与电源、计算机相连接，开启数据识别与处理功能；设立图像中被采集目标的参照目标，启动扫描设备的识别功能，构建三维坐标系；在固定范围内，对采集目标并描绘为三维图形；经过多次变换后，重新获取当前坐标，同时合并数据空间；平移、旋转、缩放获取的点云信息。

2.1.2点云数据合并

移动机器人在实际采集过程中，由于环境的复杂性，会受到目标表面特征、设备转角等因素影响，需通过不断的变换获取更加全面的目标信息。而每次变换均会生成一个单独的数据，为保证数据的完整性，本文通过建立靶标世界坐标系，实现点云数据合并。基于场景三维点云、世界坐标系具有相同空间尺度，建立靶标世界坐标系，可在世界坐标系确定跟踪目标的空间区域，达到对映到世界坐标系里的点云进行分割的目的[6-7]。

相机坐标系里的点云用pc(xc,yc,zc)代表，世界坐标系里的点云用pw(xw,yw,zw)代表，根据像素p(u,v)投射到世界坐标系的点在像素坐标系中的齐次坐标与在世界坐标系里的关系，可得到式(1)：

(1)

(2)

式中：pwl(Xwl,Ywl,Zwl)表示偏移补偿后的点云坐标；E3×3表示单位矩阵；在靶标坐标系中，Vroi表示目标区域，Vroi可通过手动测量获得，也可以通过目标物模型求解。

2.1.3点云数据处理

想要获得场景分割目标点云可将鸟瞰视角作为观测的角度观测点云，突出目标、从目标点云获得更多信息[8-9]；通过中值滤波方法确定目标阈值范围后对图像进行还原[10-11]。

结合相关性理论与滤波技术，将所有点的p(u,v)坐标作为图像灰度值，针对点云数据做选择性滤波处理：

变换到场景点云俯视角时，通过式(1)得到的世界坐标系点云pwl(Xwl,Ywl,Zwl)变为转换视角后的点云p(xu,yu,zu)满足：

(3)

(4)

(5)

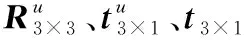
2.2 混合伺服跟踪方法

以2.1小节获取的点云数据处理为基础，采用距离函数加权方法，依据移动机器人与目标间的距离，通过视觉伺服和声呐伺服混合导航方式实现运动目标跟踪。

2.2.1视觉目标差控制

(6)

式中：机器人坐标系、图像坐标系间的转换矩阵用M代表且满足：

(7)

延伸到像素平面控制策略可表示为

(8)

2.2.2目标跟踪

通过距离函数加权可融合决策层的传感器的信息，移动机器人与目标间的距离大、小、脱离视觉传感器时相对应措施是：采用视觉导航、强化声纳信息权系数、只依靠声纳导航[15]。而单独使用视觉导航跟踪移动机器人目标时，存在对使用环境要求较高，受运行场地信息和面积的影响，导致目标跟踪时间精度都有所下降，声纳导航多用于水下目标跟踪，其在跟踪移动机器人时同样存在受外界干扰因素较强的影响，导致目标跟踪精度有所下降[16-17]。为此本文通过视觉伺服和声呐伺服混合导航方式实现运动目标跟踪。

距离函数Ri可表示为

(9)

式(9)中:Δi表示移动机器人、目标的水平距离;Δr、Δs表示按任务需求量应用不同跟踪方法的范围边界。移动机器人与目标间的距离大时，Δi>Δs时，Ri=1。移动机器人按高速υs通过视觉伺服跟踪方法跟踪运动目标，目标当前位置、跟踪位置间的水平像素差决定用ω代表的角速度，曲率表示为

ρ=[-λ(ud-uc)-jυυs]/jωυs

(10)

式中: (ud-uc)表示目标在图像平面的投影水平坐标差，jυ与jω表示移动机器人行为控制输入的特征描述子横坐标的雅可比矩阵量。jω=M12，jυ=M11，用M代表移动机器人坐标系得到图像坐标系的转换矩阵，满足：

(11)

移动机器人与目标间的距离较小时，Δi<Δs，Ri=0。移动机器人按低速υr通过声纳跟踪方法跟踪运动目标，局部网格中的目标位置夹角、移动机器人前进方向决定用角速度ω，此时的曲率ρ满足ρ=ρi：

(12)

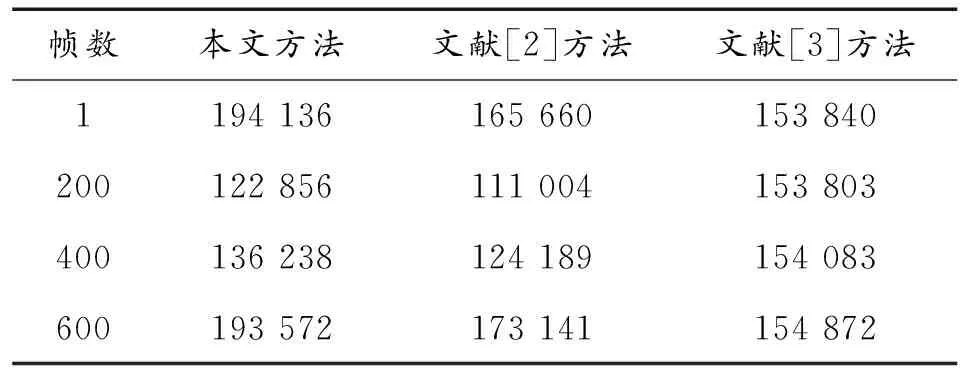
Δr<Δi<Δs时，0

(13)

移动机器人不断接近运动目标，如果要使速度(υ,ω)从(υs,ωs)到(υr,ωr)平滑过渡，则Ri要求从0到1平滑过渡。得到最终局部规划控制策略：

(14)

υs在移动机器人直行时值较大，转向时值较小。故υs可表示为

υs(ω)=υmin+(υmax-υmin)(1+tanh(π-kω|ω|))

(15)

综合考虑移动机器人运动性能、柔顺性可通过式(19)实现。移动机器人移动时最大最小速度分别用υmax、υmin代表，kω满足kω=12。

3 实验与论证

在面积为80 m2的实验室内，以移动机器人Pioneer-3DX为实验对象对运动目标进行跟踪。设置机器人的最高速度为200 m/s，最高角速度为10 (°)/s，将摄像头安装在机器人上方每隔3 s对图像进行一次采集。

表1为应用本文方法与文献[2]基于改进Camshift算法的运动目标跟踪方法、文献[3]基于ECO-HC改进的运动目标跟踪方法在第1帧、200帧、400帧、600帧条件下对点云数为30 700的图像进行分割后的点云数目记录表。

表1 3种方法分割后点云数目记录表

利用表1所示的3种方法分割后的样本数据，统计3种方法在不同分割比率下的点云分割均方根误差，结果见图1。

图1 点云分割均方根误差曲线

从图1可以看出，在相同分割比率下，应用本文方法进行点云分割的均方根误差变化曲线始终低于文献[2]方法、文献[3]方法，且曲线比较平缓。说明在相同分割比率下，应用本文方法的点云分割误差更小，更适应实际需求。

图2表示了应用本文方法得到的4种角速度下的运动目标距离精确度，该指标通过4种角速度下距离系数Ri的变化情况反映，距离系数Ri越大，跟踪精度越低。

从图2分析可得，在角速度值为6 (°)/s、8 (°)/s时，应用本文方法的距离系数Ri最小，得到的运动目标跟踪的距离精确度要高于角速度为4 (°)/s、10 (°)/s时的运动目标跟踪距离精确度，且在中心距离偏差为9像素时就达到了最高值。说明移动机器人在进行运动目标跟踪时，采用角速度6 (°)/s、8 (°)/s时具有较好的运动目标跟踪效果。

图2 运动目标距离精确度曲线

图3是应用本文方法得到的4种角速度下的中心距离误差。从图3可以看出，在角速度值为6 (°)/s、8 (°)/s时，应用本文方法得到的运动目标跟踪的中心距离误差要低于角速度为4 (°)/s、10 (°)/s时的运动目标跟踪中心距离误差，且在中心距离误差曲线无较大波动，目标跟踪稳定。

图3 中心距离误差

图4表示了机器人在无障碍物与有障碍物时的目标跟踪区域。

图4 目标跟踪区域示意图

图5表示了应用本文方法与文献[2-3]方法对图4中的目标跟踪区域进行240次实验，得到的目标跟踪区域的误差偏移量。

图5 目标跟踪误差偏移量曲线

从图5可以看出，在相同实验次数下，无论在有障碍或者无障碍情况下，应用本文方法得到的目标跟踪偏移曲线始终低于文献[2-3]方法，且应用本文方法得到的目标跟踪偏移曲线变化较平缓，无大幅度波动，而文献[2]方法、文献[3]方法的目标跟踪偏移曲线波动较大。说明应用本文方法对目标进行跟踪的稳定性更强，误差更小。