基于DNN与PCA的核动力装置故障诊断方法研究

韩 壮，马 杰，周 刚，孙吉晨，陈玉昇

(海军工程大学核科学技术学院， 武汉 430033)

1 引言

核动力装置系统复杂，发生故障时其报警系统往往会引发大量报警。由于各种报警信号往往交互出现且相互耦合，使操纵员有时难以确定系统真实的故障原因。长期以来，对核动力装置运行状态的监测与诊断采用的是传统的阈值方法，即每一个监测参数的阈值都是预先设定的，当被监测参数信号超过了规定的阈值时，就会发出报警信号或采取保护动作。然而，使用传统的阈值方法进行状态监测，当检测出异常状态时，系统可能已经发展到难以处理的地步。使用智能技术对核动力装置运行状态进行跟踪，对系统参数进行检测并分析，可以更好地辅助操纵员及时发现并诊断故障[1]。

主元分析(PCA)是一种通过简化数据集突出主要变量的多元统计分析方法，由于其结构简单灵活而广泛应用于故障诊断领域。基于PCA的故障诊断方法能对系统运行过程中动态参数的异常变化进行放大，能对刚发生的故障作出快速的反应。但是，由于传统的PCA方法缺乏故障源推理能力，故无法判断发生故障的类型、程度以及位置[2]。利用深度神经网络(DNN)的自适学习、并行处理、非线性映射以及泛化等功能，可以基于实际系统所测量的输入、输出数据进行建模，避免建立复杂系统数学模型的困难[3]。

本课题采用的研究平台是基于美国GSE公司的SimSuite Power软件的子软件THEATRE(thermal hydraulic engineering analysis tool in real-time)程序开发的分析程序，融合主元分析(PCA)与深度神经网络(DNN)2种故障智能诊断技术，研究基于DNN-PCA技术的核动力装置故障诊断方法。首先在分析DNN和PCA原理的基础上，提出基于这2种技术的核动力装置故障诊断方法，然后针对该方法进行相关的实验设计。最后分别对不同工况下的同种故障、不同程度的同种故障以及不同类型故障进行诊断研究，并对结果进行对比分析，测试DNN-PCA方法的诊断效果。

2 PCA方法

2.1 PCA方法原理

主元分析方法的基本思想是对监测参数的空间进行坐标变换，用低维模型取代高维模型实现参数的空间降维。设Xn×m为监测参数的矩阵样本(对m个参数进行了n次监测)，其协方差矩阵[cov(X)]为：

(1)

式中，Var(xj)为方差。

用相关系数矩阵R对监测数据样本进行标准化处理。

(2)

(3)

定义λ1，λ2，…，λn为R的特征值，对应的特征向量为pi=(pi1,pi2,…,pin),i=1,2,…，n。求解特征方程：

|λI-R|=0

(4)

式中，I为单位矩阵。

(5)

Y=PTR

(6)

这样可以将m维参数样本空间经过特征向量矩阵P，转化为n维特征空间的Y。X可分解为：

(7)

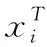
(8)

当平方预测误差值eSPE大于故障阈值δ2时，认为系统处于故障状态[3]。

2.2 PCA模型的建立

本文主要就核动力装置在不同工况下同种故障诊断效果、不同程度的同种故障诊断效果、不同类型故障诊断效果进行分析，选择与上述故障相关的主要参数，如表1所示。

表1 核动力装置参数

根据表1所列的19个测量参数，即确定19个数据采样点，选取满功率、70%功率和50%功率3种工况稳态运行下600次观测值(取样频率为每秒1次)，通过统计分析计算，得到各个参数的状态数据。

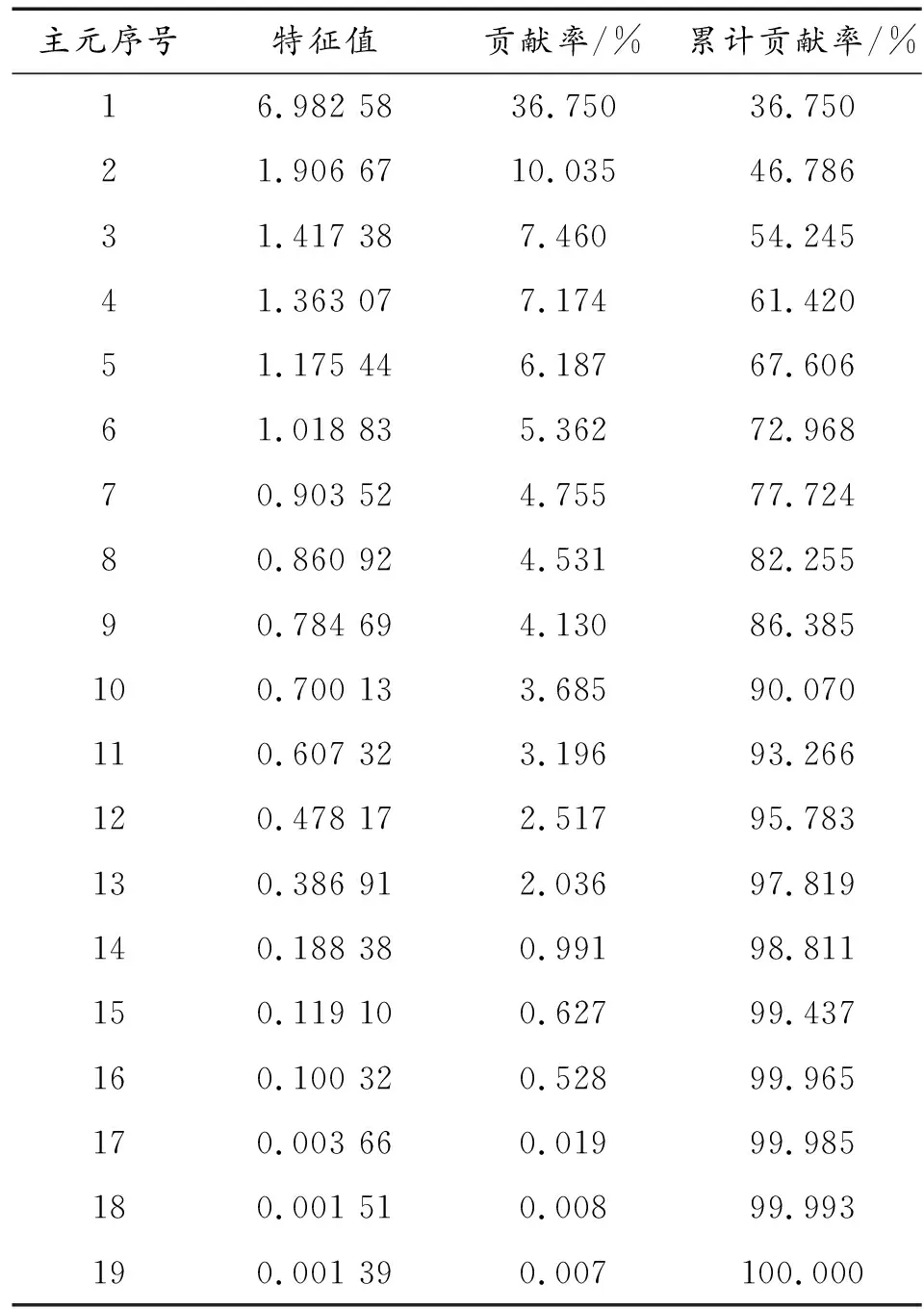
表2 主元分析模型计算的相关结果

对19个数据采样点的观测值进行标准化处理，然后计算标准化后数据矩阵的协方差矩阵，计算协方差矩阵的特征值与相应的特征向量，特征值如表2中所示(按照从大到小排序)，同时给出了对应的各个主元的贡献率及累计贡献率。图1中，条形图描述了各个主元残差贡献率，曲线表示了主元的累计贡献率，从图中可以直观的看出，前几个主元的贡献率远大于后面的贡献率，最后几个主元量的贡献率几乎为零，而且前14个主元累计贡献率已经达到98.811%。据此即可计算负载矩阵与得分矩阵，得到主元模型。

图1 主元贡献率曲线

结合表2的数据和图1所示的曲线，当选取12个主元时，累计贡献百分比即超过了95%，因此，确定主元数目为12，据此计算SPE统计量的限值，当显著性水平为α=0.05，即对应的正态分布置信度cα=95%，根据公式可计算得到故障阈值δ2=1.256 6。当平方预测误差值eSPE>δ2时，认为系统处于故障状态。

3 DNN方法

3.1 DNN结构

如图2所示，按神经网络各层结构的差异可将DNN内部分为3层，相邻层的节点间采用全连接的方式相连，同一层中节点间则不能互相连接[4]。图2中，p为编码偏移量；W为相邻层节点间的相关性系数；q为解码偏移量。

图2 深度学习神经网络结构示意图

将从核动力装置运行分析平台运行所得的数据集Xm作为输入层，各隐含层数据由编码器将原始数据集Xm层层编码得到，编码函数F为：

hm=F(Xm)=sf(wxm+p)

(9)

解码函数G为：

Hm=G(Xm)=sg(w′xm+q)

(10)

式中：w、w′表示当前网络层的权重;sf表示编码激活函数；sg表示解码激活函数。

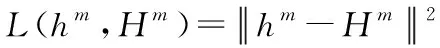
3.2 基于DNN-PCA技术的故障诊断方法

本文进行故障诊断研究的内容及流程如图3所示。

图3 DNN-PCA训练流程框图

PCA能够简便快捷地诊断系统故障的发生并进行运行参数的空间降维，DNN对于输入参数和输出参数的线性映射关系有着强大的提取能力[4]，本文所研究的方法包含以下几个步骤：

1) 将核动力装置仿真平台在不同事故工况中获取的部分运行参数数据通过PCA模型进行降维，降维后的数据集(xi,di)n用于DNN模型的训练，PCA模型的建立工作在文献[2]中已完成。其中，n表示数据的个数，xi表示第i个数据，di表示事故类型。

2) 构建具有多个隐含层的DNN网络，并使用有事故类型标签的数据集(xi,di)n逐层训练该网络，本文构建的DNN网络的隐含层为5层，具体的说明和计算在文献[4]中已经论证。

3) 输出层的维数y表示核动力装置的故障类型，DNN的输出层可通过xi计算得到，计算过程如下：

(11)

(12)

其中，θ={θ1,θ2,…,θN+1}，输入层数据xi对应输出层数据di，θN+1表示输出层的数据集。用BP算法引入δ用于训练速率的微调，以确保收敛。参数集θ更新公式如下：

(13)

4) 测试集(Xi,Di)M选取不同于训练集(xi,di)n的事故工况数据，M是测试数据的数量，Xi表示第i个数据，Di表示事故类型。将Xi作为DNN网络的输入层，经过几层编码器和隐含层得到输出层诊断结果，与事故类型对照看诊断结果是否准确，汇总后得出训练完成的DNN模型进行故障诊断的准确率。

5) 如果准确率能够达到预期则保存训练完成的DNN模型。如果诊断准确率达不到预期则可以通过改变DNN网络的的层数、每层网络的节点数等等重新进行训练，直至训练出理想的DNN模型。敏感参数分析已经完成验证分析，具体见文献[4]。

4 不同工况下同种故障诊断效果分析

选取满功率、70%功率和50%功率3种工况下LOCA事故进行分析。利用核动力模拟器仿真平台所建立的仿真模型分别对这3种工况下的LOCA事故进行计算。选择3种工况下，破口发生在相同位置、相同破口尺寸大小下的LOCA事故作为分析对象。将事故投入20 min内仿真平台产生的故障数据通过PCA降维，选取降维后的13 701组数据作为样本集输入到DNN中进行故障识别的模型训练，选取降维后的另外292组数据作为测试集，训练集和测试集中均包含三类事故数据。

如图4所示，三维空间中的数据点的分布形状和位置，可以在一定功率范围内区别核动力装置不同工况下同种故障，图中红色部分代表满功率下LOCA故障，黑色部分代表70%功率下LOCA故障，蓝色部分代表50%功率下LOCA故障。从图中可以看出，3种故障虽然各自聚集，区别明显，尤其100%功率下LOCA事故可以有效区别其他2种事故，但是70%功率下故障和50%功率下故障这两组数据交叉明显，没有较好的分类出，对此结果，分析是因为采集的核动力装置系统70%和50%功率下，当发生LOCA事故时，系统参数变化没有100%功率下系统参数变化的剧烈，导致数据变化趋势并不明显。因而在70%功率和50%功率下故障诊断结果一般。

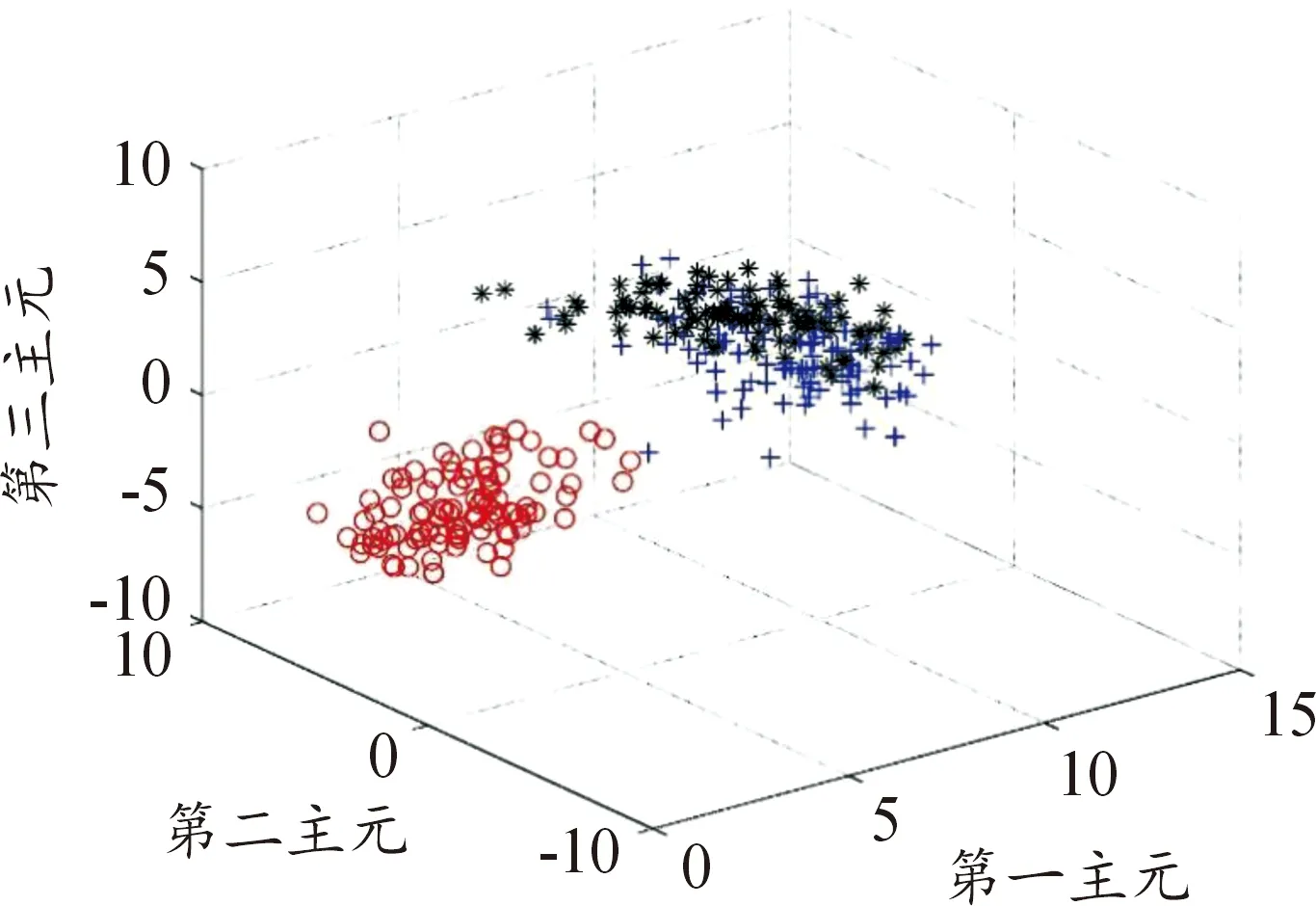
图4 同种故障不同工况下故障模式数据点的分布示意图

如表3所示，基于DNN神经网络的故障诊断模型能在核动力装置系统发生不同工况下的LOCA事故时，得到较好的诊断出结果，准确率可达到94.5%以上，但是随着核动力装置功率的下降，该模型的诊断准确率下降。

表3 LOCA事故不同工况下故障诊断结果

5 不同程度的同种故障诊断效果分析

选取满功率工况下破口尺寸分别为0.2 cm、0.35 cm和0.5 cm三种情况时的.LOCA事故进行分析。将仿真模型产生的事故数据通过PCA降维，把降维后的数据输入到深度神经网络中进行故障识别的训练和测试。选取满功率稳态情况下投入3种尺寸破口触发上述故障后的仿真数据，作为核动力装置的故障数据。将事故投入20 min内仿真平台产生的故障数据通过PCA降维，选取降维后的13 701组数据作为样本集输入到DNN中进行故障识别的模型训练，选取降维后的另外292组数据作为测试集，训练集和测试集中均包含3种故障数据。

通过图5可以看出，三维空间中的点的分布形状和位置，可以有效的区别核动力装置不同程度同种故障。图中红色部分是破口尺寸为0.35 cm故障数据，黑色部分是破口尺寸为0.2 cm故障数据，蓝色部分是破口尺寸为0.5 cm故障数据。从总体看通过深度神经网络诊断结果良好，3种不同破口LOCA事故数据能够较好的区分，3种事故的工况点分布区域呈现集中态势，区域中心有明显的差异，并且从图中可以看出，红色和黑色部分分布的更加密集，蓝色部分分布相对更加分散。结合核动力装置实际物理现象分析，核动力装置发生LOCA事故时，破口尺寸越大，系统参数变化越明显。因此可以判断深度神经网络能够较好的区别核动力装置不同程度同种故障。

图5 不同程度同种故障数据点的分布示意图

如表4所示，整体上看当核动力装置系统发生相同工况下的不同程度LOCA事故时，基于DNN神经网络的故障诊断模型都能够较好的诊断出结果，准确率达到92.8%以上，但是随着LOCA事故破口尺寸的变化，该模型的诊断准确率也发生变化。

表4 相同工况下不同破口尺寸LOCA事故诊断结果

6 不同类型故障诊断效果分析

选择满功率工况下LOCA事故、主泵卡轴事故、给水管道破裂事故、稳压器安全阀误开事故、蒸汽发生器U型传热管破裂事故作为分析对象。将事故投入20 min内仿真平台产生的故障数据通过PCA降维，选取降维后的13 701组数据作为样本集输入到DNN中进行故障识别的模型训练，选取降维后的另外292组数据作为测试集，训练集和测试集中均包含3种故障数据。

通过图6可以看出，三维空间中的数据点的分布形状和位置，可以有效的区别核动力装置正常和事故状态。蓝色部分代表LOCA事故、绿色部分代表主泵卡轴事故、红色部分代表蒸汽发生器U型传热管破裂事故(SGTR)、黑色部分代表给水管道破裂事故、紫色部分主代表稳压器安全阀误开事故。从总体上看五部分区域各种出现集中现象，五部分区域中心有明显的差异。从图中可以看出，蓝色部分、红色部分和紫色有部分耦合，这是因为当核动力装置发生SGTR、LOCA和安全阀误开时，这3个事故现象具有一定相似性，都是导致一回路安全边界的丧失。绿色部分区域变化集中，从核动力装置实际物理现象分析，因为主泵卡轴事故与其他四种事故，事故后果不一样，所以能够较好的与其他4种事故事故区别。

图6 不同事故故障模式数据点的分布示意图

如表5所示，整体上看当核动力装置系统发生不同故障时，基于DNN神经网络的故障诊断模型都能够较好的诊断出结果，准确率达到86.64%以上，但是对不同事故诊断效果也不相同，尤其2种事故的事故现象具有一定的相似性时，诊断结果的准确率会下降。

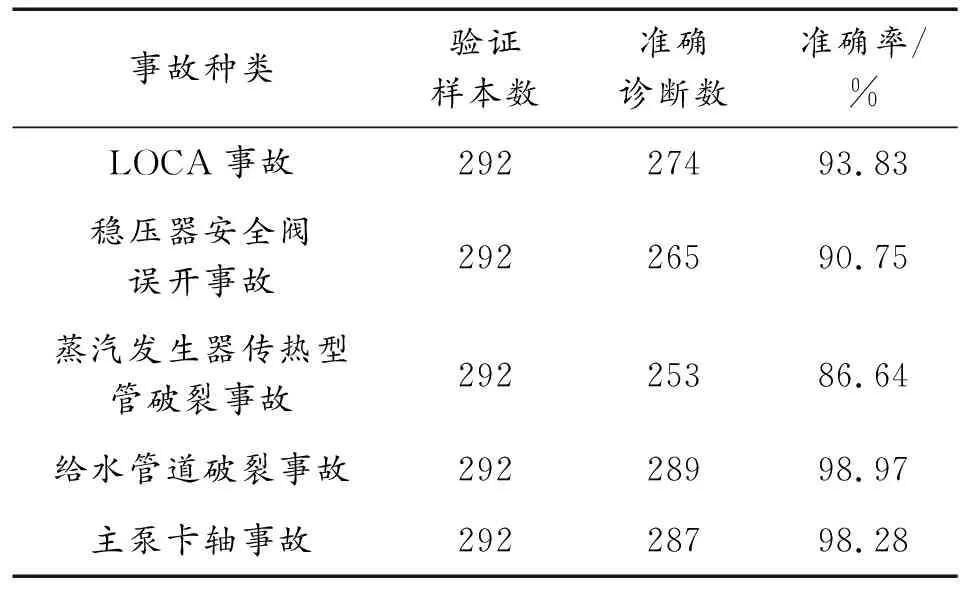
表5 相同工况下不同故障诊断结果

7 结论

研究了基于PCA和DNN的核动力装置故障诊断方法，以核动力装置为诊断对象建立故障诊断模型，并利用该故障诊断模型对核动力装置系统开展在不同工况下不同故障、不同程度同种故障以及同一工况下不同故障的诊断效果测试。结果表明，基于DNN-PCA技术的诊断方法能够快速准确地对核动力装置系统故障进行诊断，并能一定程度降低以往核动力装置故障诊断过程对专家经验的依赖性。