基于颜色统计的水果采摘机器人水果识别的研究
2022-12-14夏康利
夏康利,何 强
(江汉大学人工智能学院,湖北 武汉 430056)
0 引言
由于我国人口老龄化趋势不断加快,出生率下滑,农村劳动力严重不足。为了解决这一问题,研究人员开发了一系列不同用途的农业机器人,其中就包括水果采摘机器人。目前,中小企业销售的水果很多都是人工分拣包装,浪费了大量的人工成本,而水果采摘机器人可以节省大量的劳动力成本。
水果采摘机器人通常通过安装视觉系统来检测和识别水果[1]。水果的检测与识别是水果采摘机器人的重要任务[2]。本文提出了一种新的基于颜色的水果识别方法。传统的水果检测和识别方法在RGB颜色空间中进行[3-6]。RGB颜色空间一般采用平面矩形坐标系进行数学建模,其中三个坐标轴分别表示红、绿、蓝的颜色值。RGB颜色空间不能直接描述颜色的变化,在实际应用中受到了很大的限制[7-10]。本设计的水果识别方法采用HSV颜色空间,其中H、S和V分别代表Hue(色调)、Saturation(饱和度)和Value(明度)。HSV颜色空间封装了颜色信息,使人类更容易感知和记录颜色在色调、饱和度、明度等方面的变化[11-12]。
该方法利用了不同种类水果在HSV颜色空间中的统计特性,采用马氏距离(MD)作为识别的相似度度量。实验结果表明,与传统的基于RGB颜色统计特征的方法相比,该方法更为准确、快速。
1 水果识别方法
我们利用颜色信息来识别水果。将不同水果的RGB颜色空间转化为HSV颜色空间后,每个水果的色调满足一定的拉普拉斯分布。因此,我们可以收集每一种水果的大量彩色图像数据,然后用极大似然估计(maximum likelihood estimation, MLE)来估计每一种水果的拉普拉斯分布参数(位置参数和尺度参数),并将拉普拉斯分布作为这类水果的特征分布。对于每种类型水果的拉普拉斯分布,其置信区间为90%的拉普拉斯分布对应的马氏距离(MD)是果实的归属距离,称为特征马氏距离(characteristic Mahalanobis Distance, CMD)。即如果某一水果的拉普拉斯分布对应的输入色调值的马氏距离(MD)小于某特殊水果类型的特征马氏距离(CMD),则输入水果至少有90%的概率属于这种水果,可在实践中将该输入水果识别为该特殊水果。
1.1 水果的颜色特性
在HSV颜色空间中,H在MATLAB中表示范围从0到1的色调值。从0到1的色调值对应颜色在颜色圈上的位置。当色调值从0增加到1时,颜色从红色过渡到橙色、黄色、绿色、青色、蓝色、品红,最后回到红色。红色在0和1附近,而品红的范围是0.9到1。在实践中,根据色调色圈的周期性,当我们将0.9到1的所有色调值减去1,变成-0.1到0时,红色的拉普拉斯分布可以是连续的。因此,在实验中,将水果从0.9到1之间的色调值减去1,每种水果的颜色都符合拉普拉斯分布。
在图1至图5中,考虑了5种水果——红苹果、橘子、香蕉、绿葡萄和黄瓜。在每个图中,左侧是RGB水果颜色数据,右侧是与左侧相对应的色调直方图。可以看到,每种水果的色调可以近似于拉普拉斯分布。

图1 红苹果RGB颜色数据及色调直方图

图2 橘子RGB颜色数据及色调直方图

图3 香蕉RGB颜色数据及色调直方图

图4 绿葡萄RGB颜色数据及色调直方图

图5 黄瓜RGB颜色数据及色调直方图
图6 显示了5个水果——红苹果、橘子、香蕉、绿葡萄和黄瓜的数据集的所有色调直方图。

图6 红苹果、橘子、香蕉、绿葡萄和黄瓜(从左到右)的色调直方图
在图7中,研究组将根据MLE估计的五个数据集色调分布的相应拉普拉斯分布曲线添加到图6中。我们可以看到,不同水果的色调分布从左到右是分开的,每个都符合拉普拉斯分布。

图7 五类水果数据对应的拉普拉斯分布曲线
1.2 基于Meanshift算法的图像分割
Meanshift算法是一种非常有效的聚类迭代算法[11]。在水果色调图像中,对于每个像素点,首先计算其相邻8个点的平均偏移量。平均偏移量是一个矢量,具有大小和方向。然后将当前点更新为平均偏移方向上的点,此过程不断迭代,直到满足收敛条件。最后,将每个像素点收敛到其局部点分布密度最高的位置,从而可以分割图像的每个部分。图8显示了水果数据的Meanshift分割示例。

图8 水果RGB图像与相应的Meanshift分割图像
1.3 基于马氏距离(MD)的水果识别
马氏距离(MD)表示点与一个分布之间的距离。在水果分类和识别中,我们首先收集待分类的各种水果图像的数据集。然后从图像中分割水果,并应用最大似然估计(MLE)估计每种水果色调的拉普拉斯分布的位置参数和尺度参数。接下来,设置每种水果的拉普拉斯分布的90%置信区间,以确定水果图像像素是否属于这种水果。在实践中,对应于90%置信区间的马氏距离被用作相似性度量,这被称为每种水果的特征马氏距离(CMD)。具体解释如下:
假定μ是位置参数,b是尺度参数,则拉普拉斯分布的概率密度函数(pdf)定义为:
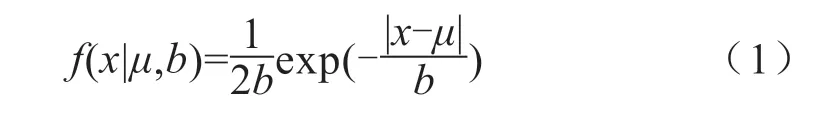
给定某一种水果在区间[μ-d,μ+d]内置信区间为90%的拉普拉斯分布,以及其对应的特征马氏距离(CMD)为m,则不大于m的马氏距离有90%概率属于该类水果。其中:

对于输入的水果图像,马氏距离Md计算为拉普拉斯分布下所有色调马氏距离的平均值:

这里N是水果色调像素的总数,xi是色调值。如果马氏距离Md﹤m,则输入水果有90%的概率属于该类水果。然后在实践中,将输入水果识别为这种水果。
2 水果识别算法
本研究的水果识别由两部分组成。一部分是根据拉普拉斯分布的90%置信区间,为每种水果设定特征马氏距离(CMD)。我们首先收集了大量不同种类水果的RGB彩色图像数据,并将水果从图像中分割出来。接下来,将分割的水果RGB颜色图像转换为HSV颜色图像。然后利用最大似然估计(MLE)估计每种水果色调的拉普拉斯分布,最后建立对应于90%概率的特征马氏距离。另一部分是识别过程。对于每个输入的水果图像,在对水果进行分割和提取后,RGB彩色图像将转换为HSV颜色空间,并针对每种水果的拉普拉斯分布计算其色调的平均马氏距离。如果该距离不大于特征马氏距离,则输入水果被识别为此类水果。
2.1 设置每种水果的特征马氏距离
特征马氏距离(CMD)是对每种水果类型的相似性度量,它是根据拉普拉斯分布的90%置信区间进行估计的。该过程将经历以下步骤:
1)收集大量不同种类水果的RGB彩色图像数据。2)对于采集的水果彩色图像,对水果主要的RGB颜色部分进行分割,去除背景等无关元素,并对水果数据集进行分类存储。3)把每一数据集从RGB图像格式转换成HSV图像格式。4)分别提取每一数据集的色调部分。5)利用极大似然估计方法估计每个水果数据集色调部分的拉普拉斯分布的位置参数和尺度参数。6)建立每种水果的特征马氏距离(CMD),对应色调数据的拉普拉斯分布的90%置信区间。整个流程如图9所示。
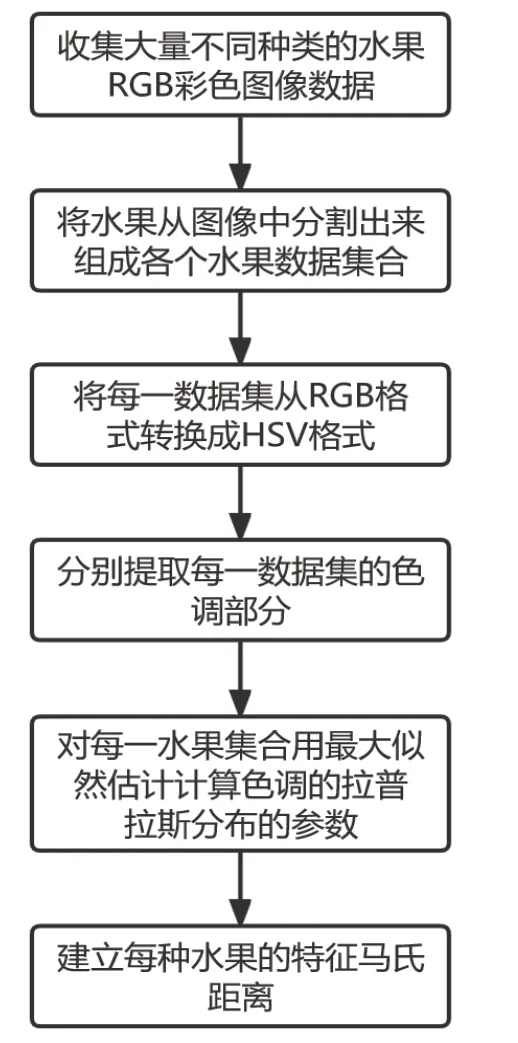
图9 各类水果特征区间计算流程图
2.2 水果识别过程
水果识别过程是为给定的输入水果图像识别类别,它包括以下步骤:
1)输入要识别的R G B彩色水果图像数据。2)使用Meanshift算法将每个水果从图像中分割出来。3)将分割后的水果图像从RGB格式转换成HSV格式。4)提取分割后的水果图像的色调数据。5)利用每种目标水果的拉普拉斯分布,计算其色调数据对应的马氏距离。6)如果对应的马氏距离小于某特定水果的特征马氏距离,则将其识别为该种水果。整个识别流程如图10所示。

图10 输入水果识别分类流程图
3 实验验证
在实验中,我们考虑了5种水果——红苹果、橘子、香蕉、绿葡萄和黄瓜。已收集了每种水果的100张测试图像,总共500张测试图像。计算了每个测试图像到每种水果的马氏距离(MD),并与5种水果的所有特征马氏距离(CMD)进行了比较。如果测试水果的MD小于某些CMD,则测试水果属于对应于CMD的这种特殊类型的水果。图11至图15显示了用Meanshift方法分割出的每种水果的5个典型单果。表1列出了5张测试图像到每种水果的马氏距离(MD)。我们可以看到,一方面,每个测试图像与其所属水果类别之间的马氏距离(MD)最小,并且小于特征马氏距离(CMD)。另一方面,每个测试图像到它所不属于的水果类别的马氏距离(MD)较大,并且对于它所不属于的水果类别,其马氏距离(MD)也要比特征马氏距离(CMD)大得多。这意味着所提出的方法运行正常。
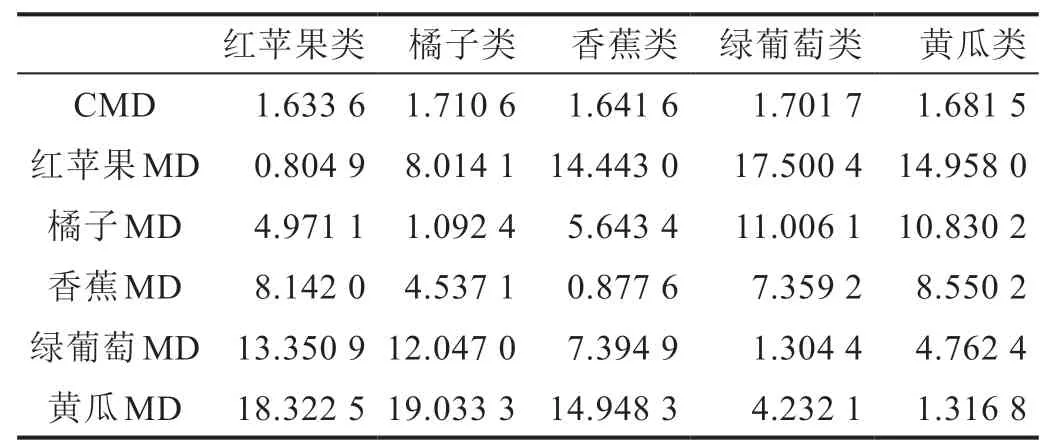
表1 每个测试图像到每种水果的马氏距离(MD)

图11 红苹果分割图

图12 橘子分割图

图15 黄瓜分割图

图13 香蕉分割图

图14 绿葡萄分割图
表2列出了500张测试图像的识别率。每种水果的识别率都在90%以上。有7个红苹果和6个橘子被错误地归类为其他类别。一般来说,错误分类的水果没有纯色表面,总是夹杂着一些斑点或色调值在大面积上有较大的变化。

表2 500张测试图像的识别率
4 结论
本文提出了一种有效的水果识别方法,该方法利用了不同水果HSV颜色的统计特性。也就是说,水果色调可以近似为拉普拉斯分布,采用马氏距离作为相似性度量。对几种常见水果的图像数据进行的实验表明,该算法具有很好的效果。然而,由于水果自然生长的多样性,在特殊情况下存在错误分类的情况,将在未来的研究中进一步解决。
