基于数字图像细观模型重构的土石混合体力学特性研究

2022-12-13贾朝军梁国栋黄娟雷明锋赵晨阳张强张建

铁道科学与工程学报 2022年11期

贾朝军，梁国栋，黄娟，雷明锋，赵晨阳，张强，张建

(1.中南大学土木工程学院，湖南长沙 410075；2.中国水利水电科学研究院岩土工程研究所，北京 100038；3.中铁五局集团有限公司，湖南长沙 410007)

土石混合体属于典型的非均匀、非均质、非连续的混合多相介质。其宏观的力学特性及细观的变形破坏机制受土石混合体内部块石的形态、大小分布、空间分布及含石量等细观结构特征影响显著。因此，研究土石混合体的力学特性应从其实际细观结构出发加以研究。在过去的几十年中，通过室内试验，国内外学者对土石混合体的力学特性进行了研究。XU等[1]研究发现，在低含石量时，悬浮于土体中的块石尚不能发挥骨架作用，试样抗剪强度主要取决于土体。IRFAN等[2]通过研究粗粒含量对土石混合物抗剪强度的影响发现，当粗粒含量较低(10%)时，粗粒含量对土石混合物的抗剪强度影响较小，可以忽略；当粗粒含量大于30%时，粗粒对土石混合体的抗剪强度有显著的提高，粗粒对土石混合体的抗剪强度开始起支配作用。许多学者开展了岩块形态、岩块比例和级配对土石混合体宏观力学性能的影响研究[3−4]。然而土石混合体颗粒组成具有多元性，颗粒粒径有的甚至到达了几米。因此不可能在实验室尺度下获得现场尺度下的土石混合体的力学特性及强度参数[5]。此外，土体和岩块的变形破坏过程，特别是土体和岩块的运动特性、内部结构的损伤等方面的研究还无法在实验室内进行。近年来，基于土石混合体现场照片重构其细观结构模型，并在此基础上借助某种数值模拟方法对土石混合体加以研究的手段逐渐兴起。随着数值模拟方法的发展，基于离散单元法的虚拟数值试验在非连续数值模拟中起到至关重要的作用[6−8]。例如，徐文杰等[9]基于现代数字图像处理技术研究了含石量对土石混合体破坏机制的影响。徐安权等[10]运用双轴压缩数值模拟试验分析了土石混合体中碎石块对堆积体强度的影响。丁秀丽等[11]通过双轴压缩数值试验模拟出土石混合体的剪切破坏形态。然而，目前基于离散元法的虚拟数值试验对土石混合体这类物质的研究还远远不够，其力学特性和破坏机制仍需深入研究。本文运用数字图像技术重构土石混合体现场真实的细观结构模型，统计分析模型的细观结构特征。在此基础上，基于重构的细观结构模型建立相应的数值模型，采用离散元方法开展不同正应力条件下的直剪试验，分析土石混合体的力学特性，观察土石混合体的宏观剪切破坏特征并分析其影响因素。探讨含石量对土石混合体抗剪强度参数的影响，从细观上探讨土石混合体的变形破坏机制。

1 土石混合体细观模型重构

1.1 图像获取及二值化处理

首先在野外拍摄典型部位的土石混合体图像，其具体操作步骤为：对预选取的拍摄部位表面进行整平、清理等处理；在适当位置放置具有一定刻度的标尺，用于确定所拍摄的图像代表的实际尺寸；利用高精度数码相机对选取的部位进行拍照，如图1所示。

图1 现场拍摄的土石混合体局部断面图像Fig.1 Local section image of soil rock mixture taken on site

受外界各种因素的影响，拍摄的图像往往存在大量噪声，导致土石间的差异并不明显，故图像处理前需进行预处理。

数字图像处理是指将图像信息转换成数字信息、并利用计算机对其进行处理的过程[12]。运用数字图像技术重构土石混合体细观结构模型一般包含2个核心过程：1) 图像二值化处理，即通过对土石混合体彩色图像二值化处理，获得其黑白二值图像；2) 石块识别与边界提取，即对二值图像中的石块进行识别并提取石块边界，进而构建土石混合体的细观结构模型。

图像识别时，需要先对图像进行HIS色彩空间转化处理，将RGB图像转化为HIS图像。HIS色彩空间是从人的视觉系统出发，利用色调(Hue)、饱和度(Saturation)和亮度(Intensity)这3个变量来描述色彩[13]。以图1所示的土石混合体图像为例，通过HIS色彩空间转化及灰度处理获得了图像在HIS色彩空间下其H，S和I 3个分量的灰度图像，见图2所示。由该图可看出，S分量的灰度图更能凸显出土石的差异。据此，文中在后续图像二值化处理中，选取S分量的灰度图进行处理。

图2 土石混合体图像在HIS色彩空间下3个分量的灰度图Fig.2 Gray images of SRM in HIS color space

二值图像属于一种特殊的灰度图像，图像中每个像素点的灰度值只有0和1这2种取值，其中0代表黑色，1代表白色。灰度图像二值化是将图像中灰度值小于某个阀值的像素点的灰度值重置为0，把大于等于这个阀值的像素点的灰度值重置为1，从而实现灰度值二值化。通过对土石混合体彩色图像进行HSI色彩空间转化和图像二值化处理后，最终可以获得土石混合体图像的二值图像。

1.2 边界处理

图像每个像素周围均有若干个邻接像素，通常将这些邻接像素所组成的集合称为该像素的邻域。常见的邻域类型有2种：4-邻域和8-邻域。而连通域是指由一系列彼此相邻的且具有相同像素值的像素所组成的集合。连通区域标记就是按照邻域类型将二值图像中的各个连通区域找出并标记[14]。对于土石混合体来说，4-邻域的连通域标记是比较合理的。对土石混合体二值图像经过连通域标记后，可将图像中每个石块所对应的连通域标识出来，每个连通域均为一个像素集合，通过对像素集合进行处理可以提取连通域的边界。本文提出了一个简单的方法来获取连通域的边界，其包括3个主要步骤：1) 对连通域中每个像素进行分解，任意一个像素均可以分解为4个边；2) 遍历所有的边，删除重复的边；3) 将剩余边有序的连接起来构成连通域的边界。

为了得到形状更为“光滑”的石块，采用YUE等[15]所提出的边界光滑处理方法对石块边界进行处理，且保证细观结构中石块的含量基本保持不变。从现场不同部位选取3个典型土石混合体图像，图片长2 750 pixels，宽2 000 pixels；所拍摄实际土石混合体长229.2 mm，宽166.7 mm。利用数字图像处理技术建立相应的细观结构模型，见表1。

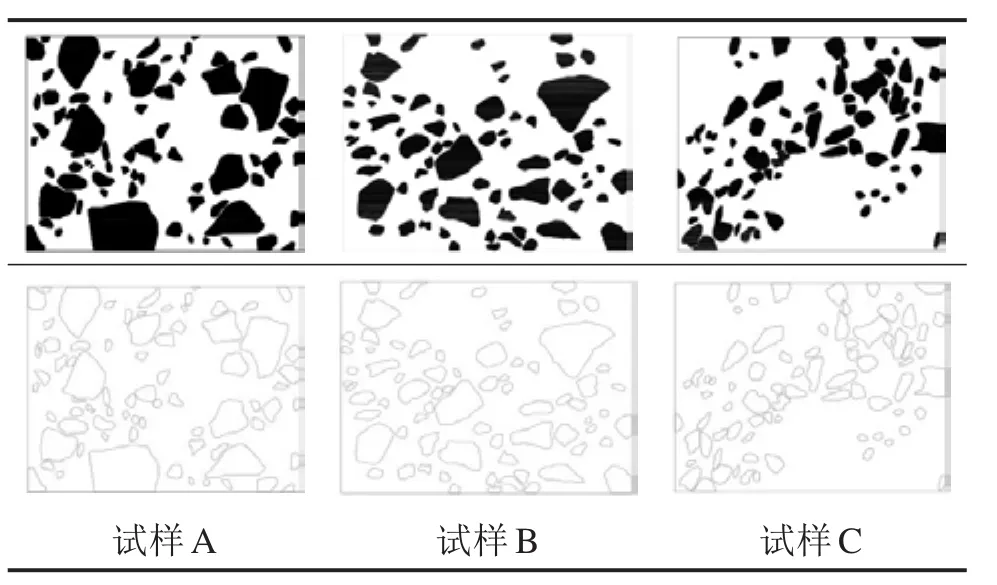
表1 典型试样细观结构模型Table 1 Meso-structural model of typical specimen

2 直剪试验模拟

2.1 数值试验装置模拟

直剪试验装置在颗粒离散元中是采用无摩擦的刚性墙体来模拟的[16−17](图3)。剪切装置包含上下2个部分，其中下半剪切盒在剪切过程中整体缓慢地向右移动，移动速度为0.000 5 m/s；上半剪切盒保持固定不动。

图3 二维直剪试验模拟装置Fig.3 Simulation apparatus for two dimetional numerical direct shear tests

采用伺服机制在1号和5号墙体上施加恒定的法向应力。颗粒离散元不能在模型上直接施加指定的应力值，需通过墙体借助伺服机制控制墙体的移动速度对模型间接地施加指定的应力值。通过伺服控制机制，实现固结过程，使试样处于一个指定的初始应力状态，并维持在直剪过程中施加的法向应力恒定。

2.2 数值试样的制备

在颗粒离散元中，材料的宏观物理力学响应是由颗粒间细观接触模型来反映的。文中选用接触黏结模型来反映土石混合体的力学特性。文中考虑石块在试验过程中不发生破碎，故在制备土石混合体数值试样时，采用PFC2D提供的clump来模拟复杂形状的石块。在数字图像重构的土石混合体细观结构模型基础上，本文提出了一种土石混合体数值试样的制备方法，每个试样的数值模型是在同一个纯土体模型基础上建立的，其中纯土体模型是由17 701个圆形颗粒组成，模型中颗粒最大半径为2.0 mm，最小半径为1.0 mm。该方法包括了以下2个主要步骤：

1) 按照典型照片所代表的试样实际尺寸，利用边界向里逐步填充方法，建立相同尺寸的纯土体试样颗粒模型。为了消除颗粒尺寸对试样宏观力学特性的影响，纯土体模型中颗粒的最大直径应小于模型最小尺寸的1/80倍；

2) 将纯土体颗粒模型和重构的土石混合体细观结构模型相叠加，遍历细观结构模型中每一个石块，判断每个石块所包含的圆形颗粒，并将每个石块包含的所有圆形颗粒组成一个clump，最终建立土石混合体离散元土石颗粒模型，见表2。

表2 典型试样数值模型Table 2 Numerical model of typical specimen

2.3 土石细观模型及参数

在颗粒离散元中，细观模型参数无法通过室内试验直接测定，只能通过对相应的室内试验曲线标定来间接获取[18−19]。通过对室内土体直剪试验和石块单轴压缩试验结果进行标定，结果如图4所示。获得的典型土石混合体的细观参数如表3所示。

表3 土石细观参数Table 3 Mesoscopic parameters of constitutive relations for soil and stone particles

图4 不同法向围压下的试验曲线对比Fig.4 Comparison of test curves between indoor tests and numerical tests under different normal pressures

3 数值模拟结果分析

3.1 应力−应变曲线特征

根据建立的不同试样的数值模型，选取标定出的土石细观参数，开展了在不同法向应力(0.2，0.4和0.6 MPa)下的数值直剪试验，试验结果如图5～7所示。

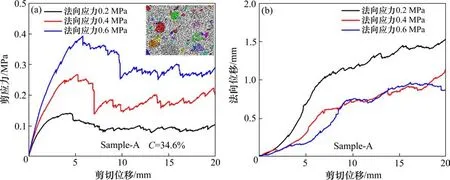
图5 试样A不同法向应力下的试验曲线Fig.5 Test curves of sample-A under different normal stresses

由不同试样的剪应力—剪切位移曲线可以看出，在剪切过程中，不同试样均经历了峰前和峰后2个明显不同的阶段，且峰后出现了一定的软化现象，这与土石混合介质现场大型原位试验结果相吻合。

峰前不同试样的剪应力−剪切位移曲线形状基本相似，总体上表现为剪应力随剪切位移增加而非线性递增。石块含量越大，峰值时的剪应力越大。

峰后不同试样的剪应力−剪切位移曲线波动较大，剪应力跳跃现象较为突出。这主要是由于试样内部土石颗粒间相互咬合作用的结果。峰值后试样内部土石颗粒间的初始咬合发生破坏，造成剪应力在峰后发生突然的跌落。其中试样A的剪应力在峰后一定位移后发生跌落，而试样B和试样C基本上是在峰后发生快速跌落。随着位移增加，土石颗粒间再次形成新的咬合，致使剪应力在局部抬升，此后新的咬合破坏，剪应力又出现跌落。法向应力越大，剪应力的跌落与抬升现象越明显。对于试样B和试样C而言，在0.4 MPa和0.6 MPa法向应力下，这一现象较为明显。

由试样的法向位移−剪切位移曲线可以看出，在剪切过程中试样表现出了剪胀的特性；试验法向应力越小，剪胀特性越明显。同时随着剪切位移的增加，试样的剪胀程度有所减弱，其中试样A表现最为明显。

图6 试样B不同法向应力下的试验曲线Fig.6 Test curves of sample-B under different normal stresses

图7 试样C不同法向应力下的试验曲线：Fig.7 Test curves of sample-C under different normal stresses

3.2 宏观剪切破坏特征

3.2.1 法向应力的影响

图8所示为试样A在不同法向应力下的颗粒位移云图。可以明显地看出试样剪切破坏后形成的剪切带，主要位于直剪试验剪切面上下一定的区域内，且剪切带存在明显的“绕石”现象。法向应力越大，剪切带厚度越大，但试样剪胀性却减小。此外，对比不同试样在直剪试验前后石块的空间位置的变化可以看出，位于剪切带内部的石块发生了移动和旋转，这也正是试样剪应力—剪切位移曲线在峰后产生较大波动的原因。

图8 不同法向应力下试样A的颗粒位移云图Fig.8 Displacement contours of soil particles for sample-A after shear failure

3.2.2 含石量的影响

图9为不同试样在同一法向应力下的颗粒位移云图。从图中可以看出，不同试样颗粒位移云图差异性较大，试样在剪切破坏后所形成的剪切带的形态和大小也差异较大。这是试样内部细观结构特征的差异性所致，主要是受剪切面附近石块的大小和空间分布影响。位于剪切带内部的石块发生了移动和旋转，剪切带也表现出了“绕石”现象。

图9 不同试样剪切破坏后的颗粒位移云图Fig.9 Displacement contours of soil particles for different specimens after shear failure

3.3 含石量对土石混合体力学特性的影响

室内和现场试验结果显示[20]，土石混合物的抗剪强度满足摩尔—库伦强度准则。图10为不同试样法向应力与剪应力的关系。抗剪强度与法向应力基本呈线性关系，表明数值模拟结果与试验结果吻合。

图10 不同试样抗剪强度确定Fig.10 Determination of shear strength of typical samples

含石量表征了土石混合体内部土石成分所占比例，是堆积体细观结构的一个重要特征，对土石混合体的力学特性和强度参数有着显著影响。为了考虑含石量对土石混合体抗剪强度的影响，文中从现场不同部位另外又增选了17组土石混合体照片，采用前述方法开展了类似的数值试验。图11为试样含石量与抗剪强度参数的散点图。

图11 试样抗剪强度与含石量的关系Fig.11 Relationship between shear strength and stone content

从图中可以明显的看出，试样的含石量越高，试样的内摩擦角越大；且含石量与内摩擦角基本呈线性关系。通过对数据进行线性拟合，得到了含石量C与内摩擦角ϕ的关系：ϕ=39.98*C+18.30。

试样的黏聚力随着含石量的增加在逐渐减小，这是因为土石混合物的黏聚力主要来自于土体。此外，从图中也可以看出，含石量与黏聚力呈线一个非线性递减的关系，通过对数据进行指数形式的拟合，得到了含石量C与黏聚力c′的关系：c′=117.23*e-5.29*C。

在进行数值直剪试验时，随着含石量的增加，土石混合体内土石颗粒之间的咬合作用不断加强，表现为内摩擦角加的增大；而含石量增加导致细颗粒含量减少，黏土颗粒之间的黏聚力下降。

4 细观变形破坏机制分析

通过分析剪切过程中试样内部颗粒间接触力力链演化过程，可以清楚地了解试样内部土石颗粒间接触力的相互传递演化过程。

图12绘制为试样A在0.2 MPa法向应力下不同剪切位移时试样内部颗粒间接触力大小与方向分布图。随着剪切位移的增加，接触力分布形状由圆形逐步变为类椭圆形，且椭圆的长主轴方向与剪切方向成一定的反向角度(图12(b)至图12(f))。在剪应力到达峰值前，剪应力随着剪切位移逐渐增大，试样内部颗粒间的接触力沿着抵抗剪切方向也将逐渐增大，导致椭圆的长短轴之比增大，椭圆形状变得扁平(图12(b)至图12(c))；剪应力到达峰值后，随着剪切位移增加，剪应力由峰值逐渐减小到残余值，试样内部颗粒间的接触力沿着抵抗剪切方向也将逐渐减小，导致椭圆的长短轴之比减小，椭圆形状变得粗壮(图12(d)至图12(e))；残余值后，随着剪切位移的增加，剪应力大小基本不变，试样内部颗粒间的接触力也将保持不变，此时椭圆的长短轴之比基本不变，椭圆形状非常相似(图12(e)至图12(f))。

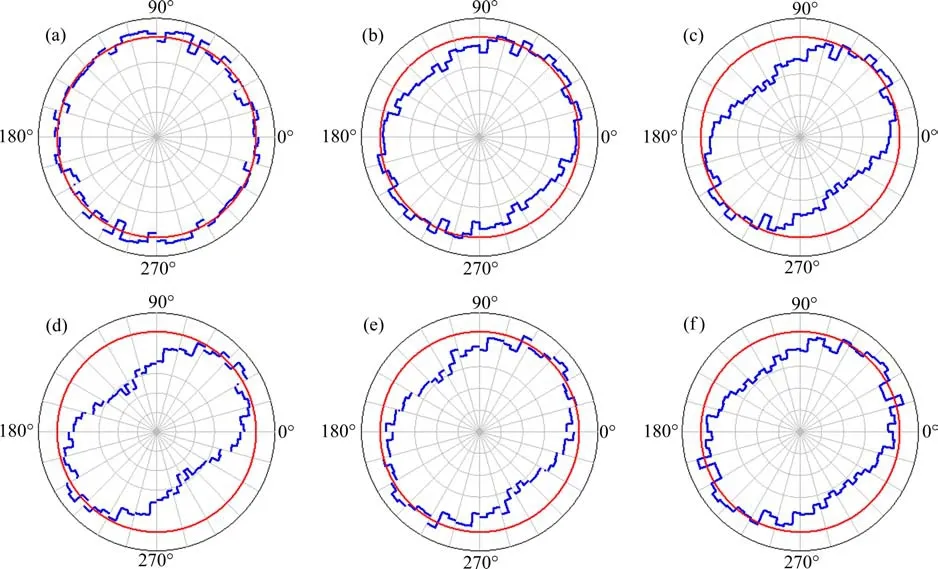
图12 不同剪切位移下试样内部颗粒接触力大小与接触方向分布图Fig.12 Distribution of size and direction of contact force between particles for sample A at different shear displacements

经过分析可知，在试验初始阶段，试样内部土石颗粒间接触力的大小和方向分布较为均匀，此时剪应力是由土体和石块两者共同来承担的且承担剪应力大小基本相同；随着剪切位移的增加，为了抵抗剪应力土石颗粒间接触力的方向发生了明显的偏转，同时颗粒间接触力的大小分布也发生了一定的变化，石块所承担的剪应力比土体颗粒所承担的剪应力较大，尤其是大石块承担了更多的剪应力；当试样发生剪切破坏后，随着剪切位移的继续增加，试样内部颗粒间接触力变化不明显。