高速列车过桥线缆位姿变化的扭转特性研究
2022-12-13崔志国张强谭磊沈超肖合婷周伟
崔志国,张强 ,谭磊,沈超 ,肖合婷 ,周伟
(1.中国中车青岛四方机车车辆股份有限公司,山东 青岛 266111;2.中南大学 交通运输工程学院,湖南 长沙 410075;3.中南大学 轨道交通安全教育部重点实验室,轨道交通安全关键技术国际合作联合实验室,轨道交通列车安全保障技术国家地方联合工程研究中心,湖南 长沙 410075)
高速列车过桥线缆是实现车−车通信与电力传输等功能的电力系统重要组成部分,列车在高速运行通过曲线、道岔及坡道等复杂线路时,车辆间的复杂运行姿态导致线缆夹持根部频繁扭转和弯曲,线缆随列车服役时间加速老化、疲劳和失效,往往达不到保质期限就要在短时间内进行更换,增加了列车检修次数,严重影响列车的正常运行。因此,通过开展高速列车车端空间位姿变化的过桥线缆相对扭转特性研究,对于掌握线缆随服役时间的扭转疲劳特性具有重要意义。目前,针对线缆空间位姿的研究主要集中在线缆模拟装配领域,张永涛等[1]利用悬链线理论对悬挂约束状态下的线缆进行研究,建立了二维线缆的静态模型并利用坐标变换算法将其转化为3D线缆装配模型,该模型可以计算出线缆关键点的张力大小;王发麟等[2]针对线缆变形大的特性,提出一种基于精确Cosserat模型的柔性线缆物理特性建模方法,实现了线缆的动力学方程的求解与验证;IMPOLLONIA等[3]提出了一个模型,可用于获得弹性缆绳在均匀分布的载荷和许多定向点力作用下的变形形状;刘佳顺等[4]从拉伸、弯曲和扭转等方面考虑,在Cosserat弹性杆理论的基础上建立了活动线缆干扰力矩最小的布局优化模型;金望韬等[5]分析了在光滑平面约束下活动线缆运动的约束方程,得到分布力作用下的活动线缆Kirchhoff平衡方程并建模;VAEZZADEH等[6]利用节点松弛法对松弛的电缆结构进行三维非线性动态分析;马立元等[7]提出基于质点−弹簧仿真模型对柔性线缆在拾取和牵引等操作过程中进行运动仿真,其实验结果表明线缆仿真能很好地模拟线缆长度保持特性和抗弯性能;谢世富等[8]基于柔性线缆的特性建立质点−弹簧模型,并提出线缆分层精确碰撞检测算法,可快速准确地判断碰撞是否发生及发生的位置;ZHOU等[9]针对多股捻制绞线力学模型提出一种新型有限元分析方法,采用分段截面轨迹节点扫略和滚动节点梁单元映射实现单股绞线有限元拓扑模型的自动生成。在线缆疲劳研究的其他领域,油气开采作业中连续管的弯扭压及其耦合导致的疲劳失效问题[10−11],海底电缆敷设过程中电缆的弯曲刚度、海床刚度、风浪流作用方向和入水角度等对海缆运动、张力和曲率的影响特性[12−13],多维转动机械臂线缆的弯折与扭转疲劳状态模拟[14],导管式电缆结构的非线性静态和动态分析[15−16]等也是研究的热点。在高速列车线缆的位姿变化与疲劳研究方面,中南大学针对车端过桥线缆运动状态进行了实车运行视频监控,发现明线运行时车体小幅度摆动导致车端线缆向内风挡或车体外侧方向小幅偏移,而在列车通过小曲线半径线路时车间风挡区域摆动幅度显著加大,车端间距改变后造成缆线被牵拉、挤压;邓艳俊等[17]发现过桥线缆的自重下坠力在列车通过弯道时产生曲挠和摆动冲击力,使电缆产生向远离连接器方向的轴向应力,该应力会集中存在于连接器对过桥线的夹持处;张玉芳等[18]设计车端线缆疲劳试验台模拟过桥线缆的扭转变化情况,通过互相垂直的传动臂模拟横向和纵向运动,该实验台可实现最不利扭转工况下的线缆疲劳评估。综上,目前对柔性线缆的运动建模与疲劳仿真评估已有一定的研究基础,但列车车端过桥线缆的空间位姿变化的相对扭转特性研究鲜有报道。因此,本文提出夹持点间线缆弯曲和旋转组合的位姿解耦与运动复原,考虑不同出线角度下线缆空间位姿变化,构建线缆夹持点的相对扭转理论模型并进行试验验证与扭转特性分析。
1 理论解算
列车行经曲线、道岔和坡道等线路时,车间的相对横摆、点头导致过桥线缆夹持点的空间位置与姿态发生变化,具体表现为沿运行纵向与水平横向的夹持点间距改变及摆转,该类几何参数可以通过车辆参数、线路参数及运行工况进行理论计算,但不同出线角与几何位姿变化带来的线缆弯扭力学响应特性,缺乏关联计算理论模型。为此,需要建立不同线缆初始形态下,夹持点空间水平面位置变化与线缆夹持点相对扭转特性之间的理论计算模型。
1.1 基本假设
线缆的周向自由度定义为线缆绕轴线的旋转自由度,线缆扭转角定义为在释放线缆夹持端的周向自由度后,由于夹持端的横向位移引起线缆根部绕自身轴线的转角。当夹持端线缆周向自由度被约束时,线缆不会发生旋转,但由于夹持端的横向位移,线缆横截面将承受绕轴线方向的扭矩。为度量该扭转角,需释放夹持端线缆周向自由度,夹持端横向移动后线缆根部产生的绕自身轴线的自由转角即为扭转角,该扭转角的参考面为过根部轴线、且与当前线缆所在平面垂直的法向面,不同出线角下扭转角的计算可转换为初始位置与位姿变化后位置的参考面相对夹角计算。
过桥线缆两端通过线夹分别固定在两车水平对称位置,初始横向无错位(图1(a)),在夹持点相对运动过程中,线缆的长度足以适应自身产生的弯扭变形。

图1 线缆运动分解示意图Fig.1 Cable motion decomposition diagram
线缆的几何参数定义如下。
1) 纵向间距L:夹持点沿车长方向距离;
2) 出线角β:夹持部位的线缆轴线与水平面之间的夹角(0°~90°);
3) 横向间距W:由于车间运动导致沿水平横向发生的位移。
当线缆出线角β=90°吊挂(图1(b))、纵向间距为L时,夹持点发生横向位移W对应的线缆端部截面状态如图1(c)所示,在运动过程中夹持点线缆截面的旋转自由度被约束。
为便于分析位姿变化前后的夹持根部扭转,将运动过程分解为弯曲和旋转的组合运动。
第1步:纵向弯曲。夹持点之间的纵向间距由L增至位姿变化后的(图1(d));
第2步:垂向旋转。线缆绕顶部夹持点整体顺时针旋转至最终位姿状态(图1(e)),该旋转过程为线缆根部无扭转变形的自由过程。
由于组合运动过程中线缆根部没有发生相对扭转变形,因此位姿变化的相对扭转角计算等效为组合运动线缆截面与初始线缆截面的相对扭转计算。定义初始位置的夹持点连线与位姿变化后的夹持点连线夹角为α,考虑双夹持点相对于初始位置的扭转,线缆横向窜动后的线缆根部相对扭转角为2α(α=tan‒1(W/L))。
考虑线缆出线角在水平面的极限情况,当出线角β=0°时,线缆两端夹持部位的轴线共线,线缆横向窜动后,两夹持点轴线虽发生移动,但仍相互平行保持在一个平面(如图2所示),根部截面相对于各自轴线没有发生旋转,因此相对扭转角度为0°。
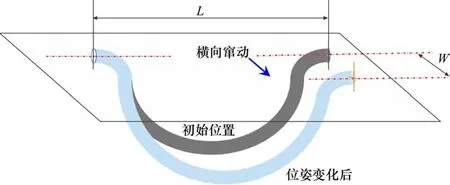
图2 水平极限出线角的线缆运动Fig.2 Cable movement in the horizontal limit case of the exit angle
根据0°和90°极限出线角的线缆根部扭转特性分析,其他任意出线角的根部扭转为介于0°和90°出线角扭转计算的理论模型。
1.2 扭转角解算
参考出线角90°位姿变化分析方法,将任意出线角下线缆夹持点的空间运动分解为纵向弯曲与垂向旋转,如图3所示。以线缆夹持点的初始坐标点和位姿变化坐标点为顶点(O,C,E点),构建六面体的顶面;以夹持点位姿变化坐标点C,E和旋转点线缆轴线与E点垂引线的交点D为顶点,构建六面体的对角面。
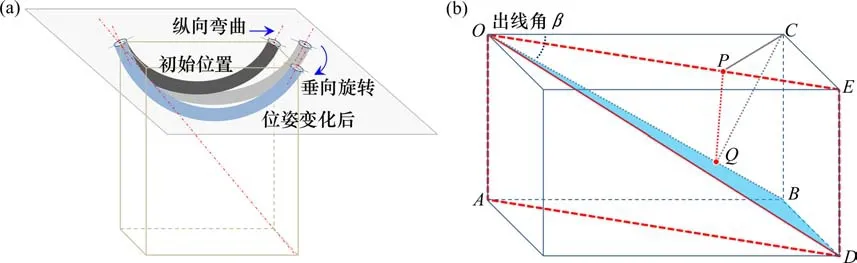
图3 任意出线角线缆空间位姿变化的空间六面体几何表征Fig.3 Geometric representation of spatial hexahedra with spatial positional changes of cables at arbitrary exit angles
显然,在构建的六面体中,线缆根部出线角β=∠COB,纵向间距L=|OC|,横向间距W=|CE|,面OABC为初始位置线缆所在平面,面OADE为旋转后线缆所在平面,OB与OD分别为初始位置与旋转后线缆夹持点O的轴线。
显然,要计算初始位置与垂向旋转线缆截面的相对扭转,需要各自选定轴线的一个参考面,通过计算2个参考面的相对转角确定2根轴线的相对扭转。
选取过根部轴线且与线缆所在平面垂直的法向面作为参考面:在初始位置,过轴线OB且与面OABC垂直的法向面为面OBD,定义该面为初始轴线OB的参考面(记为面η);在垂向旋转后位置,定义过轴线OD且与面OADE垂直的法向面为旋转轴线OD参考面(记为面λ)。不难推断,线缆绕根部O的垂引线整体无扭转旋转后,初始参考面η运动变换到了旋转参考面λ,但参考面λ无法在六面体中直接绘制。考虑到初始参考面η与旋转线缆所在面OADE交于旋转轴线OD,且面OADE⊥λ,参考面η与参考λ的转角计算,可等效为参考面η与参考面λ的法向面OADE夹角的余角计算,即面OBD与面OADE的夹角余角。
在几何方法中,可以通过计算2个面的法线夹角作为2个面的夹角。在面OCE中过点C作直线CP⊥OE;由于OA⊥面OCE,有CP⊥OA。因此,CP⊥面OADE,CP为面OADE的法线。在面OCB中过点C作直线CQ⊥OB;由于DB⊥面OBC,有CQ⊥DB。因此,CQ⊥面OBD,CQ为面OBD的法线。
综上,面OBD与面OADE的夹角计算转换为法线CP与CQ夹角计算问题,即△CPQ中内角∠PCQ的求解问题。
在六面体中,根据出线角定义六面体高记为:

在△OCE和△OCB中,由等面积法可得:

通过△OED和△OPQ的余弦定理,间接计算边长|PQ|。在△OED中,由余弦定理得:
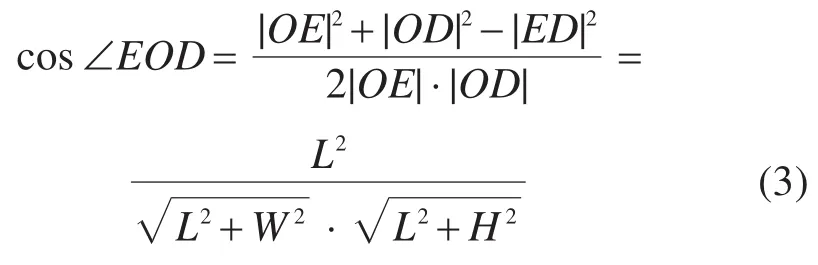
在△OCE与△OCB中,由三角形相似有:

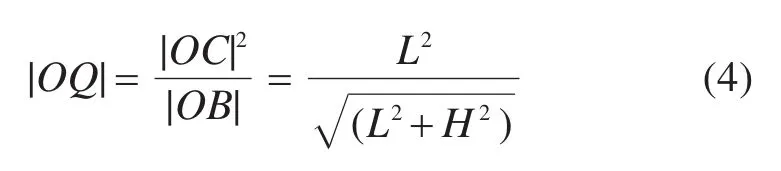
在△OPQ中,由于∠POQ=∠EOD,根据余弦定理有:
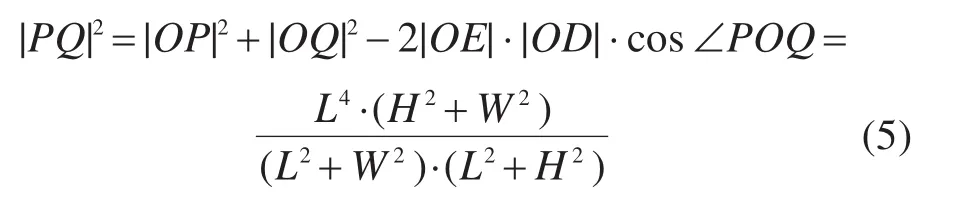
在△PCQ中,由余弦定理计算得:

将式(1)代入式(6),得:

根据定义,线缆夹持点单端扭转角为∠PCQ的余角:
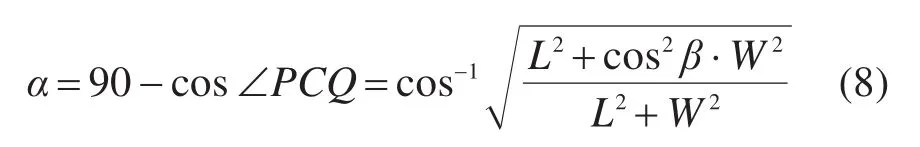
式(8)给出了线缆夹持点相对扭转角2α的计算模型。显然,当出线角β=0°时,单端扭转α=0°;当出线角β=90°时,单端扭转α=tan‒1(W/L),与前文极限出线角的分析结论一致。
结合车辆实际尺寸参数(见图4),线夹间纵向间距L可表示为:L=P−2·C,其中P为车钩长度,C为线夹安装点到车钩安装点的纵向距离。结合式(8),扭转角计算公式为:

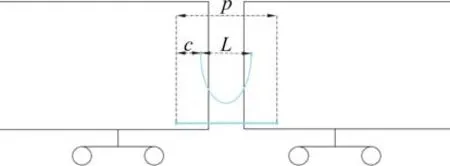
图4 车端关系参数图Fig.4 Vehicle end relationship parameter chart
2 试验验证
为模拟车端过桥线缆在车间运动产生的横向与纵向位姿,通过导轨结构实现夹持点在2个方向的平动,通过转动副结构实现线缆夹持点的不同出线角。该线缆夹持点位姿模拟试验台,可实现不同运行纵向间距、水平横向间距和出线角情况下,线缆夹持点的相对扭转角测量。
2.1 位姿机构设计
线缆位姿模拟试验机构设计为“目”型框架结构,框架采用40 mm×40 mm铝合金型材加工,在型材上开设滑动导槽(图5(a)~5(b))。导槽旁安装有位移刻度钢尺及对准线进行示值,以实现横向导轨整体沿纵向导轨的运行纵向移动(图5(c)),线缆线夹沿横向导轨的水平横向移动(图5(d));横向导轨与纵向导轨配合副设计为平移与旋转组合配合副,平移副实现上述的纵向位移模拟功能,转动副通过角标尺与示值指针实现不同出线角的模拟(图5(c))。
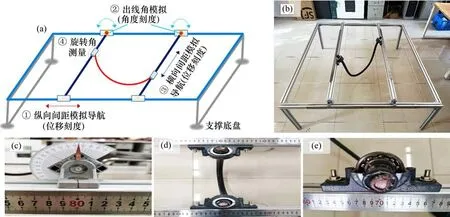
图5 线缆加持点位姿模拟试验机构Fig.5 Cable holding point posture simulation test mechanism
为实现线缆运动位姿下根部扭转的测量,线夹与线缆之间设计为滚动轴承配合(图5(e))。其中,轴承外圈与线夹过盈配合,轴承内圈与线缆过盈配合,使用滚动轴承配合的目的是为了将线夹模拟为实际线缆状态,而将线缆模拟为整体无扭转自由旋转状态。在线夹内表面安装有角刻度尺,在线缆外表面安装有示值指针,通过读取线缆位姿发生后的指针示值,即可测量单端扭转(图5(e))。
2.2 模拟试验工况
位姿模拟试验的实车线缆长度为960 mm,通过试验台模拟出线角在15°~90°(15°为间距)范围内,纵向间距由300~600 mm,横向间距由0~400 mm变化设计正交试验工况。具体工况的控制参数及范围定义如表1所示。
表1中,7种出线角、7种纵向间距与11种横向间距参数组合下,总计进行7×7×11=539种位姿模拟工况的扭转角测量,试验结果按照7种出线角进行归类分析。
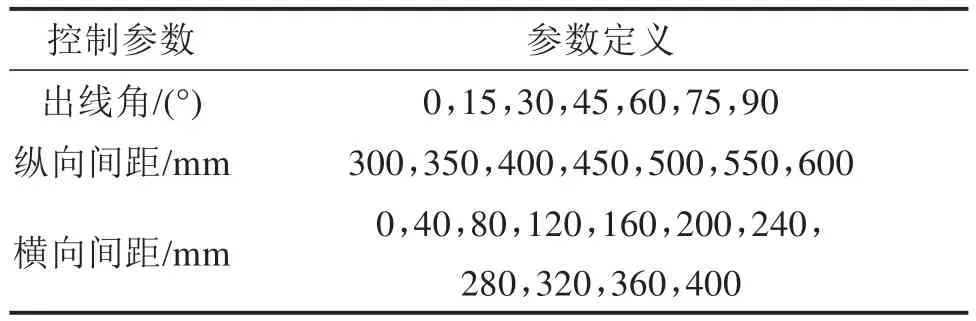
表1 位姿模拟试验工况Table 1 Posture simulation test conditions
2.3 试验结果分析
每种出线角下,将各个位姿工况的纵向间距L,横向间距W与出线角β代入式(8)计算线缆单端扭转角,与实测扭转角度(图6(a))进行对比。
以横向间距作为横坐标、纵向间距作为纵坐标、单端扭转角作为垂坐标作图,其中,试验测试的扭转角绘制为面云图,理论计算扭转角绘制为黑圈白底的散点。不同出线角下,单端扭转角的理论计算与测试结果对比如图6(b)~6(h)所示。

图6 单端扭转角理论计算和试验测量对比云图Fig.6 Experimental measurement of single-end torsion angle and comparison cloud of theoretical calculation
由线缆单端扭转角的理论与试验对比结果可知,两者随出线角、横纵向间距的变化趋势吻合较好,均是随着出线角的减小,扭转角呈降低趋势。同时,通过计算不同出线角位姿模拟工况下的理论计算与试验测试结果的误差值,统计每种出线角工况下所有误差的均值与最大值分布柱状图如图7所示。
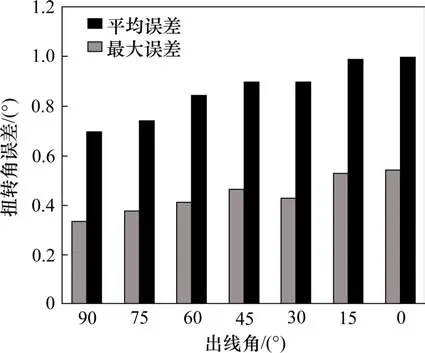
图7 单端扭转角理论与试验结果误差柱状图Fig.7 Histogram of error between theoretical and experimental results of single-end torsion angle
经统计,所有试验工况下单端扭转角的理论与试验结果误差均值、最大值分别在0.5°与1.0°以内,且随着出线角的减小,两者的误差整体呈增大趋势。一方面,由于线夹角度尺与线缆指针之间的示值读取存在人为误差;另一方面,随着线缆出线角的降低,横纵间距的变化会导致线夹与线缆之间滚动轴承的径向力增加,一定程度影响了线缆的整体旋转,加大了误差。但这种影响较小,理论与试验之间的最大误差仍在1.0°范围以内,表明提出的过桥线缆位姿变化下根部相对扭转理论计算模型准确、可靠,可满足工程设计与评估要求。
选取线缆夹持点最小纵向间距300 mm,最大横向间距400 mm的位姿模拟工况,读取0°~90°不同出线角下的单端扭转角理论计算值与试验测试值,绘制散点变化趋势图如图8所示。由拟合结果可知,线缆单端扭转角随根部出线角的减小呈非线性下降趋势,且出线角度越小,单端扭转角下降幅度越大,但同时线缆根部的小出线角度会降低线缆的弯曲半径,不利于弯曲载荷下的线缆服役性能的正常发挥,因此需要综合考虑进行线缆布置的设计。
图8 单端扭转角随线缆出线角变化规律Fig.8 Law of single-end twist angle with the cable out angle change
3 结论
1) 考虑不同线缆根部的出线角,通过将线缆的空间运动分解为夹持点间线缆的纵向弯曲与垂向旋转组合运动,建立线缆空间位姿变化的空间六面体几何表征模型,在此基础上构建了夹持点相对扭转角的理论解算模型。
2) 设计了线缆位姿模拟试验台,可实现线缆夹持点周向自由度、横/纵向自由度与出线角度变化,并通过滚动轴承配合实现线缆与线夹之间的相对偏转角度的测量。
3) 通过线缆位姿模拟试验台测试了15°,30°,45°,60°,75°和90°共6种出线角下总计539种位姿模拟工况的单端线缆夹持点扭转角,理论计算值与试验测试结构趋势吻合较好,两者误差值在1.0°以内。
4) 研究提出的线缆空间位姿变化相对扭转角理论计算模型准确、可靠,可为高速列车线缆布设的高效设计提供科学手段;同时,通过智能视觉识别对高速列车运行中的车间线缆夹持点位姿进行监控,可将位移姿态谱转换为线缆根部的扭转载荷谱,为线缆结构的疲劳安全评估提供理论依据。
