基于高斯贝叶斯网络的大型钢桁梁桥损伤识别

2022-12-13袁明贵辛宇王佐才段大猷

铁道科学与工程学报 2022年11期

袁明贵，辛宇, ，王佐才, , ，段大猷

(1.合肥工业大学土木与水利工程学院，安徽合肥 230009；2.安徽省基础设施安全检测与监测工程实验室，安徽合肥 230009；3.安全关键工业测控技术教育部工程研究中心，安徽合肥 230009)

钢桁梁桥作为大跨径桥梁的首选桥型之一，具有结构稳定和架设方式灵活等特点。主桁结构主要由拉杆和压杆组成，单个构件主要承受轴向荷载为主，能充分发挥材料的强度，在增强结构刚度的同时能够减轻自重。但由于桁架结构本身杆件数量众多，空间布置形式复杂，截面形式多样，材料参数不确定，以及测量噪声等因素的影响，使得对大跨钢桁梁桥的安全状态评估研究变得十分复杂[1−2]。为了实现钢桁梁体系的安全状态评估以及失效模式判别，基于健康监测技术的方法被应用于此类型桥梁结构。近年来，随着健康监测系统在大型桥梁结构中的应用越来越广泛，面对庞大的数据量和众多维度的信息，基于数据驱动的桥梁结构安全性能评估技术得到了广泛应用[3−4]。其中，基于机器学习理论的桥梁结构损伤识别理论得到了重要应用[5−6]。聂振华等[7−8]提出了联合移动主成分分析与传递熵的识别方法进行桥梁结构损伤定位，该方法成功应用于梁式桥梁结构的损伤识别；单德山等[9]采用聚类分析方法对桥梁结构的损伤进行定位分析，该方法应用于移动车辆引起的桥梁振动分析中；LEI等[10]提出一种基于卷积神经网络的结构损伤识别方法，能够对未知荷载作用下的结构损伤进行识别。本文针对大型钢桁梁桥各桁架单元在运营期间的安全性能展开研究，考虑桁架体系的杆件数量多，空间布置形式复杂，给此类型桥梁结构的损伤识别带来一定困难[11]。将高斯贝叶斯网络应用于大型钢桁梁桥的损伤识别中，不仅能够通过若干单元的监测数据实现对未监测部位的数据推断，同时，能够根据结构的数据推断结果，进一步对结构的状态变化进行评估，从而快速实现对此类型桥梁结构的安全性能评估[12−13]。本文以某大型公铁两用钢桁梁桥为算例，通过模拟结构发生单点损伤、多点损伤以及不同损伤程度，验证本文方法的有效性[14]。

1 连续型变量贝叶斯网络

1.1 高斯贝叶斯网络(GBN)

GBN网络是图论和概率论的结合，通过系统地描述随机变量之间的关系以进行概率推断[15]。贝叶斯网络可用数学表达式表示为：

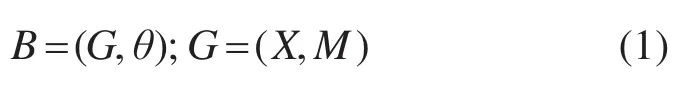
其中：G=(X,M)表示有向无环图；X为无环图中所有节点的集合；M是各节点之间有向连接的集合，网络B通过参数θ定量描述节点之前的变量关系。

GBN网络作为连续型变量贝叶斯网络，假设网络中各节点变量服从正态分布，即X={X1,X2,…,Xn}服从正态分布N(μ,R)，则连续变量的联合概率分布可以表示为：

其中：μ为变量集X的n维均值向量；R为n×n维协方差矩阵；f(X)为联合概率分布。当节点变量均服从正态分布时，联合概率分布f(X)由n个一元正态分布的乘积表示。即：

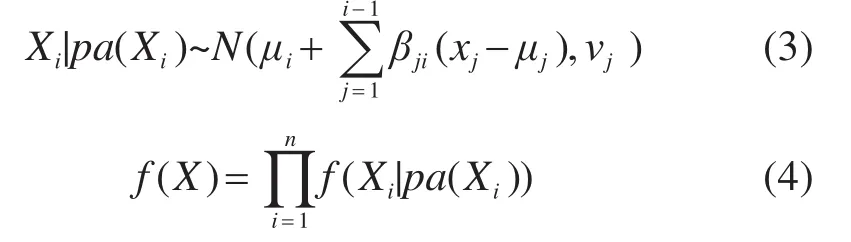
其中：μi是Xi的均值；βji是Xi和其父节点pa(Xi)的回归系数；νi是Xi在其父节点条件下的方差；βji是用来衡量Xi和Xj的关系强度；pa(Xi)(i=2,…,n)是Xi的所有父节点集合。

GBN网络的主要目的是在一组变量中获得目标变量的条件概率分布，当需要求解节点变量Xi(Xi∈X)在一个新的证据E∈X下的后验分布时，则有：

当再次输入观测数据时可以根据已经生成的贝叶斯网络对未知变量进行推断。μi和μe是Xi和E的均值，σii和σee是Xi和E的方差，σie是Xi和E之间的协方差。当需要求解节点Y(Y⊂X)在新证据E(E∈X)条件下的联合概率分布时，则Y在给定E=e条件下的概率分布为带参数的多元正态分布，如式(6)～(7)所示。

因此，基于上述公式，可在给定的新证据条件下，对未知节点的数据特征进行推断，并得出在新证据条件下未知节点的数据分布结果，从而达到利用已知节点数据推测未知节点信息的目的[16]。

1.2 GBN网络模型的构建

GBN网络的构造方式主要有3种：1) 直接确定贝叶斯网变量节点，并通过工程师经验确定贝叶斯网的结构形式和网络参数；2) 先确定贝叶斯网络节点，再通过大量的训练数据学习贝叶斯网的结构和参数，属于全数据驱动方法；3) 先确定贝叶斯网络节点和结构，通过训练数据学习网络参数，这种方式可显著提高机器学习的学习效率。

在本研究中，考虑到钢桁梁桥在移动荷载作用下的传力路径较为明确，因此，选择采用第3种方式进行GBN网络构建。对于桥梁结构，影响移动荷载作用效果的因素主要包括车重、车速以及轨道不平顺度等。在构建GBN网络时，将这些因素作为贝叶斯网络中的1级父节点(以I节点表示)；其次，考虑到跨中挠度作为衡量桥梁行车振动效应的关键指标之一，因此将桥梁跨中挠度值作为网络的2级父节点(以II节点表示)；最后，将2级节点向周围单元进行拓扑，将与此节点相连单元的最大轴力作为2级节点的子节点(以III节点表示)，即形成向下的3级网络节点构造形式。基于上述分析，构建的GBN网络结构如图1所示。

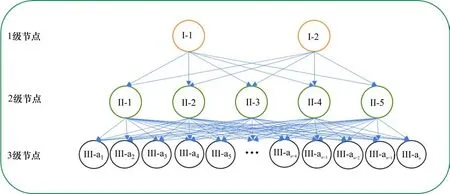
图1 GBN网络结构图Fig.1 GBN network architecture diagram

1.3 基于GBN网络的钢桁梁桥损伤识别研究

对于大型钢桁梁桥，由于结构体系中存在大量不同形式的结构构件，可以通过建立GBN网络将需要分析的桁架单元作为网络节点，并利用桥梁在随机车辆荷载作用下的峰值响应与各桁架单元的峰值应力建立拓扑关系，构建适用于钢桁梁桥损伤识别的GBN网络模型。本文基于GBN网络的钢桁梁桥损伤识别研究大致可表述为：1) 首先基于有限元分析，获得桥梁结构在移动荷载作用下的结构响应数据，包括跨中挠度和杆件峰值应力等；2) 构建以移动荷载、跨中挠度以及杆件峰值应力为节点的GBN网络模型，利用有限元分析获取训练数据，实现网络训练；3) 获取健康状态下桥梁重要杆件的应力监测数据，并利用GBN网络实现对全桥桁架单元的峰值应力推断；4) 损伤条件下，利用GBN网络和重要杆件的应力监测数据，对全桥桁架单元的峰值应力进行推断；5) 构建损伤指标，利用步骤3和步骤4中的推断结果，实现桥梁结构的损伤定位及损伤程度量化。

为了对桥梁进行损伤识别，定义的损伤指标如式(8)所示。

其中：yhealthi为健康状态下，桥梁ith杆件的应力峰值推断结果；yi为运营条件下，桥梁ith杆件的应力峰值推断结果；DIi为桥梁结构ith杆件单元的损伤评定指标。

2 钢桁梁桥车桥耦合振动分析

2.1 有限元模型建立

以五跨公铁两用钢桁梁桥为研究对象，桥跨布置为(128+3×180+128) m，下层桥面为四线铁路，设计时速为120 km/h，采用ZK荷载(中国客运专线标准活载)；上层为双向6车道公路，设计荷载为公路-I级。依据桥梁设计资料，建立该连续钢桁梁桥的空间有限元模型，如图2所示。其中，有限元模型的主桁结构采用beam188单元进行模拟；上、下弦杆为箱型截面，腹杆为箱型和H型截面；桥面采用shell63单元模拟，吊杆采用link180单元进行模拟；钢材屈服强度为370 MPa，弹性模量设置为210 GPa。全桥总计采用不同截面桁架单元共53种，13 808个节点，22 100个单元。桥面节点与桁架单元采用刚臂单元进行连接，吊杆与弦杆采用共节点方式连接，对吊杆施加初应力荷载模拟实际吊杆中存在的初拉力。

图2 钢桁梁桥有限元模型Fig.2 Finite element model of the steel truss bridge

2.2 汽车-桥耦合振动效应分析

基于建立的公铁两用钢桁梁桥有限元模型，首先开展汽车荷载作用下的车桥耦合振动分析。考虑到主桥上层为6车道设计，在模拟汽车荷载作用时，将各车道车辆简化为单点弹簧−质量模型；然后，在公路荷载作用下，开展不同车速和车重条件下的汽车−桥耦合振动效应分析。

在开展汽车−桥耦合振动效应分析时，分别考虑车重、车速等因素对桥梁振动效应的影响。首先固定车速为80 km/h，分别对车重为40，45，50和55 t的4种工况开展研究。基于钢桁梁桥的有限元模型，得到4种工况下的挠度计算结果，如表1所示。通过表1可知，在汽车荷载作用下，桥梁各跨跨中挠度值随着移动荷载质量的增加而增加，同时钢桁梁桥上、下层桥面的跨中变形较为一致。类似地，固定车重为50 t，分别对车速为50，60，70和80 km/h工况下的车桥振动效应进行分析，结果如表1所示。由表1可知，相较于车重因素，车速对桥梁跨中挠度的影响较小，且边跨跨中挠度值总体低于中跨跨中。

表1 不同车重及不同车速下各跨跨中最大竖向挠度Table 1 Maximum mid-span deflection of each span under the different vehicle weights and speeds mm

2.3 列车−桥耦合振动效应分析

在进行列车-桥耦合振动效应分析时，列车荷载采用标准的中国铁路专线活载，荷载大小采用2列DF4型机车(东风4型内燃机车)、KZ70(KZ70型石砟漏斗车)满载货车组合的方式，具体列车编组方式为DF4+11KZ70+DF4。由于考虑到在真实铁路桥梁的测试过程中，采用的试验荷载一般为标准的列车荷载，因此，本研究采用固定车重的列车模型进行相应分析。当列车轴重确定之后，分别对车速为60，80，100和120 km/h条件下的列车−桥耦合振动效应进行分析。基于有限元分析结果，计算的钢桁梁桥跨中竖向挠度的时程响应曲线如图3所示。由图3可知，在列车荷载作用下，桥梁跨中最大竖向挠度介于95～97 mm之间，且随着车速增加，主桥跨中达到最大位移的时间逐渐缩短；此外，当列车行驶至次边跨时，引起主桥跨中产生向上的挠度值，最大挠度为25.43 mm。此外，仔细观察图3可以发现，随着车速提高，主桥跨中最大竖向挠度表现为先增大后减小，总体呈现上升趋势，但是跨中的挠度变化与车速不呈明显的线性关系。

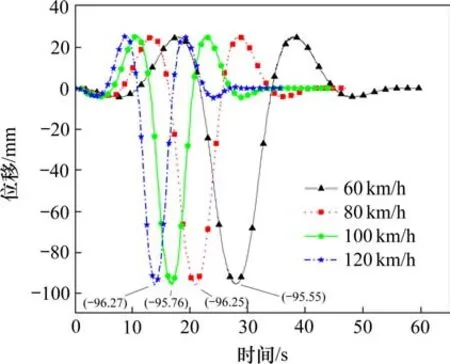
图3 不同车速工况下桥梁动挠度时程曲线Fig.3 Dynamic deflection of the bridge under the different vehicle speeds

同时，为考虑轨道不平顺度对列车-桥耦合振动效应的影响，本文假定列车车速为80 km/h，分别对3类轨道不平顺度工况下的桥梁振动效应进行分析。通过有限元计算，得到钢桁梁桥跨中动挠度时程曲线，如图4所示。由图4可知，在车速、车重一定时，随着轨道不平顺度的增加，主桥跨中动挠度的波动及峰值响应增加较明显，且最大竖向挠度由96.25 mm增加至98.35 mm。

图4 各类不平顺度工况下桥梁跨中挠度结果Fig.4 Calculated mid-span deflections for various types of unevenness conditions

3 基于GBN网络的钢桁梁桥损伤识别研究

基于建立的钢桁梁桥有限元模型，分别计算桥梁结构在不同移动荷载工况下的振动数据[17−18]，如汽车−桥耦合振动分析以及列车−桥耦合振动分析等，提取的桥梁振动数据主要包括：1) 主桥各跨跨中的峰值位移响应；2) 主桥桁架单元的峰值应力响应。利用获得的训练数据对建立的GBN网络进行训练，然后，基于训练后的GBN网络，进一步开展钢桁梁桥的损伤识别研究。考虑到汽车荷载与列车荷载的差异性，在进行钢桁梁桥的损伤识别研究时，将单独考虑汽车和列车荷载作用下的分析结果。

3.1 基于汽车荷载作用的钢桁梁桥单点损伤识别

在桥梁结构损伤识别之前，首先需要构建合适的GBN网络模型。本文选取具有3级节点的GBN网络模型，其中，1级节点对应移动荷载(包括车重和车速)，2级节点为钢桁梁桥各跨跨中节点的最大竖向挠度，3级节点为各桁架单元的峰值应力。在训练数据提取时，假定所有节点变量均服从正态分布，其中，假设车重变量为G1(单位：t)，服从G1～N(45,10)分布，车速变量为V1(单位：km/h)，服从V1～N(65,15)分布。通过随机采样，生成500组符合上述规则的样本组合，并利用有限元模型对不同样本组合作用下的桥梁响应数据进行计算。为了降低GBN网络的训练成本，本研究仅对结构受力较大的99根桁架单元进行分析，选择的桁架单元位置分布如图5所示。基于提取的500组训练数据，对初始GBN网络进行训练，并获得训练后的GBN网络，如图6所示。依据图6可以看到，网络的3级节点对应了选取的99根桁架单元的峰值应力响应，对应的杆件编号如图5所示。当GBN网络训练完成之后，便可以利用训练后的GBN网络对钢桁梁桥进行损伤识别。

图5 选择的99根桁架单元位置分布图Fig.5 Locations of the selected 99 truss elements

图6 汽车荷载作用下的GBN网络训练结果Fig.6 Training results of GBN network under vehicle load

由于在GBN网络的3级节点中仅考虑了99根桁架单元的峰值应力，因此，在进行桥梁结构的单点损伤模拟时，选择的损伤位置需要包含在99根桁架单元内。因此，本文随机选择了钢桁梁桥3号跨跨中位置的50号桁架单元作为损伤位置，并将该单元的弹性模量降低20%，模拟结构发生的损伤。

然后，基于健康状态下的桥梁有限元模型，利用质量为50 t的单点弹簧−质量模型，以70 km/h的速度匀速通过钢桁梁桥，获取主桥各跨跨中外侧对应的15根桁架单元(如图5所示)的峰值应力数据。为了模拟测量误差对实际监测数据的影响，在获取的峰值应力数据中添加了5%的随机误差。然后，将实测数据输入到训练后的GBN网络中，利用网络节点之间的拓扑关系，对剩余84根杆件的峰值应力进行推断，推断结果和实测结果的相对误差如图7所示。通过图7可知，基于训练后的GBN网络，能够精确地对桥梁剩余杆件的峰值应力进行推断，且最大推断误差控制在2.21%以内。

图7 基于GBN网络的预测误差Fig.7 Prediction errors based on the GBN network

利用考虑桥梁损伤的有限元模型，对车重50 t，车速70 km/h条件下的车桥耦合振动效应进行分析，获得上述15根桁架单元的峰值应力数据，并加入5%的随机误差模拟真实监测数据；然后，将监测数据作为新的证据输入到GBN网络中，获取剩余84杆件的应力推断结果，与模型健康状态下的推断结果对比如图8所示，基于等式(8)获得的损伤指标计算值如图8(b)所示。由图8(a)和图8(b)可以发现，当车重和车速已知时，利用15根桁架单元的应力监测结果能够推断出剩余桁架单元的峰值应力数据，并通过构建的损伤指标，能够有效地实现钢桁梁桥的损伤定位。

图8 基于GBN网络的损伤识别结果Fig.8 Damage identification results based on the GBN network

3.2 基于列车荷载作用的钢桁梁桥单点损伤识别

本节开展列车荷载作用下的钢桁梁桥损伤识别研究。在进行GBN网络构建时，1级节点分别对应轨道不同平顺度和车速，2级节点和3级节点与3.1相同。在生成网络训练数据时，假设车速变量为V2(单位：km/h)，样本服从V2～N(90,50), 轨道竖向不平顺度设置为变量D2，本文共对3种轨道不平顺作用下的列车−桥耦合振动效应进行研究。基于不同车速和轨道竖向平顺度，随机生成300组参数样本，并利用有限元模型对不同变量组合作用下的桥梁响应数据进行计算，并提取1～99号桁架单元在300组列车荷载工况下的峰值应力，以及主桥各跨跨中的最大竖向位移。基于获取的300组数据，完成对GBN网络的训练。然后，利用有限元模型，对车速100 km/h，2级轨道不平顺条件下的列车−桥耦合振动效应进行分析，并提取主桥各跨跨中外侧的15根桁架单元的峰值应力数据，通过对获取的应力数据中添加5%的随机误差模拟实测值。然后将15个应力实测值作为输入，利用训练后的GBN网络对剩余杆件的应力状态进行推断，网络预测值与有限元模拟结果的误差值如图9所示。通过图9可以发现，训练后的GBN网络能够准确实现桁架单元的内力估计，且最大误差推断控制在2.54%以内。

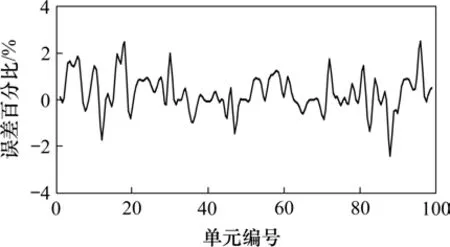
图9 列车荷载作用下GBN网络预测误差Fig.9 Predicted errors of GBN network under train loads

与汽车荷载作用工况类似，将50号桁架单元的刚度折减20%，用于模拟桥梁发生的损伤；然后，利用桥梁结构的损伤模型，对车速100 km/h，2级轨道不平顺条件下的列车−桥耦合振动效应进行分析，并获取15根桁架单元的峰值应力作为监测数据。将应力监测数据作为GBN网络的输入，获取剩余桁架单元的应力推断值，并利用等式(8)，计算列车荷载作用下的损伤指标值，计算结果如图10所示。由图10可知，基于训练后的GBN网络，能够实现列车荷载作用下的损伤识别。此外，通过对比汽车荷载作用下的损伤识别结果可以发现，在汽车荷载作用下，损伤位置处的指标计算值为17.23，大于列车荷载作用下的识别值，且相较于未损伤杆件的计算值，识别效果较明显。其中，主要原因是由于简化为单质量-弹簧模型的汽车荷载对局部桁架单元的刚度变化灵敏度较高，当单质量模型作用到桥梁结构的局部损伤区域时，峰值应力的变化较明显。然而，列车荷载由于载荷作用范围大，荷载传递区域较大，同时参与受力的杆件数量较多，导致局部损伤引起的应力变化被分散。因此，通过上述分析可知，尽管2类方法均能实现钢桁梁桥的损伤识别，但基于汽车荷载作用的损伤识别结果要优于列车荷载。

图10 列车作用下的损伤识别结果Fig.10 Damage identification results under train loads

3.3 不同损伤程度对识别结果的影响

为验证汽车荷载作用下，基于GBN网络的钢桁梁桥损伤识别的有效性和可靠性，本文进一步开展不同损伤程度下的桥梁结构损伤识别。与上述章节类似，仍以50号桁架单元发生损伤为例，分别考虑单元发生5%，10%以及20%的损伤。以3类不同损伤程度的桥梁模型为基础，利用本文提出的方法开展钢桁梁桥损伤识别研究。基于汽车-桥耦合振动分析，获取15根桁架单元的峰值应力数据，通过添加5%的随机误差，模拟桥梁结构的实测数据。分别将3类损伤工况下的实测数据作为输入，代入到训练后的GBN网络模型，得到3种工况下的损伤指标计算值，如图11所示。由图11可知，损伤指标计算值随着单元损伤程度的增加而增加，分别为6.28%，9.31%和17.23%。通过上述研究发现，基于本文提出的损伤识别方法不仅能够准确实现结构的损伤定位，同时能够对结构发生的损伤程度进行量化。

图11 不同损伤程度条件下的识别结果Fig.11 Damage identification results for different damage conditions

3.4 多点损伤条件下的钢桁架桥损伤识别

为了验证本文方法对钢桁梁桥多点损伤识别的有效性，进一步开展基于GBN网络的钢桁梁桥多点损伤识别研究[19]。为模拟桥梁结构的多点损伤工况，分别将钢桁梁桥的32号桁架单元刚度折减10%，将50号桁架单元刚度折减20%；然后，利用健康和损伤状态下的有限元模型，开展桥车−桥耦合振动分析，获取15根桁架单元峰值应力数据，并加入5%的随机误差模拟真实监测数据。将实测数据代入到先前训练好的GBN网络中，对未知桁架单元的应力进行推断，并进一步根据应力推断结果计算各单元的损伤指标值，结果如图12所示。由图12可以发现，本文方法能够准确实现钢桁梁桥的多点损伤定位，且2个损伤位置处的指标计算值分别为8.51%和13.82%。因此，通过上述分析可知，本文方法不仅能够有效地实现钢桁梁桥的损伤定位，同时能够对单元的损伤程度进行量化。