基于态势利导的需求响应自学习优化调度方法

明威宇，李 妍，程时杰，龙 禹，徐 菁，王少荣

（强电磁工程与新技术国家重点实验室，华中科技大学，湖北省武汉市 430074）

0 引言

随着中国电力市场化改革的快速推进［1］，用户可选择需求响应（consumer choice resource，CCR）基于自身意愿主动参与到电力市场各项业务中［2-3］。通过对CCR 的调度，可以将负荷侧资源配合电网运行加以充分利用，从而减少网损［4］、提升设备使用寿命［5］、改善用户的用电体验［6］，在满足网侧精益化管理的同时实现用户侧降费提质的需求。但CCR 受用户主观意愿和负荷动态物理特性等多因素影响［7-8］，其优化调度需要考虑多目标综合优化和系统运行的安全约束，协同众多变量优化求解，其优化问题为具有复杂动态约束的混合整数非线性规划模型，在配电网随机运行方式下求解时，存在场景组合激增的问题，求解的复杂度随求解时段数成指数增长，难以找到最优解［9-10］。

随着近年来数据驱动的机器学习方法的发展［11-12］，深度强化学习（deep reinforcement learning，DRL）在多个领域的序贯决策优化问题中得到了广泛应用［13-15］。已有不少学者利用DRL 将电力系统随机优化决策问题映射至马尔可夫决策过程（Markov decision process，MDP）模型，以自学习方式予以求解。文献［16］对DRL 应用于需求响应业务的可行性与方法进行了探讨，提出了基于DRL 的需求响应业务开展架构。文献［17-18］关注到需求响应业务侧负荷的联合竞价及定价问题，利用基于DRL 的深度确定性策略梯度方法［18］，基于MDP 对负荷的联合竞价及定价问题进行建模，建立动态竞价响应函数，通过自学习历史数据优化终端用户用电行为。文献［19］利用改进深度确定性策略梯度算法计算楼宇级控制策略，建立调度中心-负荷聚集商-楼宇级控制单元-用户的调度架构，将电采暖动作、用户费用及调度成本等纳入MDP，从而基于DRL 调度用电采暖参与需求响应。文献［20］依托演员-批评家结构的DRL 算法，将工业设施中储能设备的电能状态、工业设备动作情况纳入MDP，利用DRL 制定工业设施的最佳能源管理策略，实现需求响应侧业务优化管理。文献［21］基于DRL 将用户不满意度、售电商经济收益纳入MDP，实现了激励型需求响应的补贴价格决策优化。文献［22］将电动汽车作为需求响应资源，将电动汽车充放电动作、电网功率波动值等情况纳入MDP，基于DRL 实现了需求响应的优化决策。综上所述，DRL 求解CCR 优化问题的有效性已得到广泛关注。

本文基于态势利导的需求响应自学习优化调度方法，首先，分析以电压安全运行为约束条件，以供电公司经济补偿和停电次数最小为目标的CCR 群组节点优化调度数学模型；然后，构建MDP 模型的CCR 群组节点态势感知元组和态势利导函数；进而，通过对历史负荷数据曲线的泛化处理，DRL 算法在ε-greedy 策略和经验池机制下训练态势利导函数，以预测电网运行状态以及模拟用户行为，通过自趋优决策实现多组待选CCR 群组的优选及其所包含节点的优化调度；最后，以IEEE 33 节点为算例，对比分析竞争深度Q 网络（dueling deep Q network，DDQN）结 构 和 深 度Q 网 络（deep Q network，DQN）结构的CCR 群组优选求解策略，体现了DDQN 结构DRL 算法的优越性，对比DDQN 结构下不同规模的样本数量的CCR 群组优选求解策略，验证了所提方法适应多时间断面复杂场景的有效性。

1 需求响应优化调度的数学模型

在保证CCR 群组节点响应后电压运行在安全范围的前提下，供电公司因CCR 群组节点调度给予用户经济补偿将影响其售电利润，且用户侧停电次数不能过多，因此优化模型目标为电网经济补偿与停电次数最小。优化调度的目标函数如式（1）所示，其中第1 项为供电公司经济补偿函数，第2 项为停电次数惩罚函数，由于两者量纲不同，且数值存在数量级差距，故将其归一化处理。考虑到当CCR 群组节点响应后，电网节点电压应运行在合理范围内，电压运行惩罚函数如式（2）所示。

式中：NCCR为CCR 群组节点集合。本文定义响应状态集合为{响应，未响应}。

在日调度周期T中，CCR 群组节点（即功率可观测节点）有n个，在其响应后对c个节点电压进行观测，在每个时间断面的运行方式所满足的潮流约束见附录A，针对c个节点的电压，需要针对2n个数据样本，在2n个状态空间中选择一组优化状态。况且日调度周期T中如果有w个时间断面，考虑到相邻时间断面的停电次数和供电公司售电利润的优化目标，故在一个周期内，需针对2nw个数据样本，在2nw个状态空间中选择一组优化状态。因此，电网运行状态随机性会导致场景组合激增，求解的复杂度随求解时段数呈指数增长，优化模型难以找到最优解。

2 态势感知元组及态势利导函数

本章基于MDP 建立自学习智能体态势感知元组（S，A，R），其中S为态势感知获取的状态集，A为响应状态动作集，R为环境理解函数，基于态势感知元组构建态势利导函数，通过自趋优态势利导实现CCR 群组的优选及其所包含节点的调度优化。

1）态势感知获取的状态集S

以配电网节点电压和CCR 群组节点的响应功率为感知量，配电网状态和CCR 群组中节点的状态构成状态集S，如式（4）所示。

3）环境理解函数R

为实现CCR 群组优化调度目标，建立的环境理解函数R包括供电公司售电利润函数、响应状态函数以及电压运行回报函数，如式（5）所示。

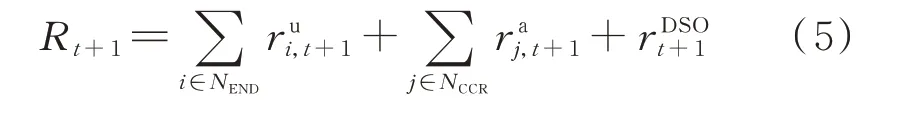
式中：Rt+1为在t+1 时刻的环境理解函数值，反映上一时刻响应状态的优劣。

4）态势利导函数

在态势感知的基础上建立态势利导函数，自学习智能体通过环境理解函数的激励与惩罚实现决策优劣的训练学习，从而逐步实现自趋优决策。态势利导函数如式（10）所示。

式中：p为控制策略；ω和b为DRL 算法参数；m为经验池容量；st∈S为t时刻环境的状态；at∈A为t时刻CCR 群组节点的响应状态。

式中：|A|为响应状态总数；Relu（x）=max（0，x）为线性整流函数；ω0为价值函数中与配电网状态相关的参数；ω1为价值函数中的结构参数；ω2为优势函数中与配电网状态相关的参数；ω3为优势函数中与响应状态相关的参数；b0至b3为偏置量。

3 多随机场景下CCR 的优化调度决策

配电网随机运行方式下求解时，为适应多时间断面下的复杂场景，本章对历史负荷数据曲线进行泛化，基于泛化后的数据，通过时序差分法更新迭代预设值矩阵，利用ε-greedy 策略选取最优动作，并引入经验池机制保证神经网络学习最新的观测状态。

1)负荷数据曲线泛化

本文在初始负荷的基础上，对非CCR 群组节点，根据其节点峰谷功率差值进行叠加随机负荷，叠加基础值ΔPl，t如式（15）所示：

式中：ΔPl，d为节点l的峰谷功率差值；PL，t为t时刻系统负荷需求；PG，t为t时刻根节点输入功率；Nnode为配电网的节点集合。

假设非CCR 群组节点中节点π峰谷功率差值ΔPπ，d最大，将其作为平衡节点，其他非π节点且非CCR 群组节点l'可叠加的功率ΔP'l'，t如式（16）所示：

式中：l'∈Nnode∩l'∉NCCR，l'≠π；μ为［-1，1］区间内的均匀分布值；ΔPl'，d为节点l'的峰谷功率差值。

负荷数据曲线泛化后，各非CCR 群组节点功率如式（17）所示：

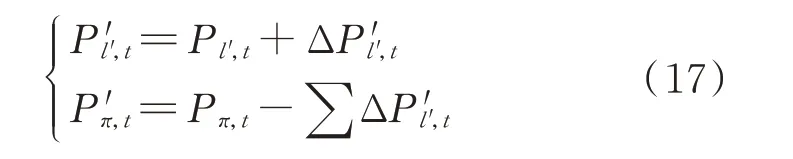
式中：l'∈Nnode∩l'∉NCCR，l'≠π；Pl'，t和P'l'，t分别为泛化前、后节点l'在t时刻的功率；Pπ，t和P'π，t分别为泛化前、后节点π在t时刻的功率。

2)时序差分法机制

时序差分法搜索CCR 群组优化调度策略如图1所示。阶段①初始状态s1经过动作ay至状态sy，由式（5）计算R，并根据式（11）更新预设值矩阵，进入阶段②，并重复上述计算过程。基于Q-learning 算法［23］，当已知优化响应状态空间与训练次数逐渐增大时，算法将逐步收敛，预设值矩阵迭代更新过程如式（18）所示。预设值及历史训练样本生成流程图如附录B 图B1 所示。

图1 时序差分法搜索机制Fig.1 Searching mechanism of temporal difference method

3）ε-greedy 策略

训练过程中，学习初期随机选择动作从而积累观察样本，ε-greedy 策略如式（19）所示：

式中：randomA表示从响应状态动作集A中随机选取 动 作；Ttr为 训 练 总 次 数；ttr为 当 前 训 练 次 数；β为［0，1］之间的随机数；ε为固定常数。

4）经验池设定

为了加快DRL 算法训练速度与精确度，对经验池采取以下设定：

（1）经验池设置容量上限，从而消除样本采集时间接近而造成的强相关性。当产生样本数量超过经验池容量时，则剔除掉最早的观察样本再存入新样本。

（2）经验池设置观察值，当训练次数小于观察值时，不抽取训练样本。当经验池中样本数超过观察值时，则从中随机抽取小批量的观测样本，开展人工训练。

5）CCR 群组优化调度策略求解

当观测状态由st变为st+1，进行以下3 个判断步骤得到供电公司售电利润函数、响应状态函数以及电压运行回报函数的数值。首先，判断U(i)END，t+1是否大于0.93Ue，根据式（6）计算电压运行回报函数

式中：x=0，1，2，3。

在高维数据场景下态势利导函数趋于收敛时，算法给出的CCR 群组节点状态响应空间可被视为该组CCR 群组节点在配电网调度下的最优状态空间。优化求解流程图如附录B 图B2 所示。

4 算例分析

4.1 随机场景

本文基于IEEE 33 节点系统分析随机场景，如图2 所示。算例分析将分别针对15 min 采样间隔和30 min 采样间隔进行优化策略求解，通过不同采样间隔形成不同规模的样本数量，验证所提方法的有效性。在图1 中，节点17、21、24、32 处安装电压量测装置，节点13、14、16、29、30 以及31 作为CCR 群组节点与供电公司签订合同构成CCR 群组，根节点及CCR 群组节点安装功率量测装置。在日调度周期中，针对4 个节点的电压，需要在64 个状态空间中选择一组优化状态。当量测装置数据采样间隔为15 min 时，日调度周期中存在96 个时间断面，需在日周期内的2576个样本数据中，从2576个状态空间中进行策略优选。当数据采样间隔为30 min 时，日调度周期中存在48 个时间断面，需在日周期内的2288个样本数据中，从2288个状态空间中进行策略优选。

图2 基于DDQN 结构的CCR 群组节点的优化调度Fig.2 Optimal scheduling of nodes in CCR group based on DDQN structure

配电网的分时电价（购电和售电）以及所签订的合同内容分别见附录C 表C1 及表C2，CCR 群组见表C3。为了尽量模拟用户用电的真实场景，体现用户负荷运行方式的多样性，算例模型中节点的实际日负荷曲线来源于IEEE 欧洲低压试验馈线［24］。

4.2 算法参数及分析

1）算法参数

2）态势利导函数收敛分析

分别采用DDQN 结构与DQN 结构的DRL 算法的态势利导函数衰减对比如附录D 图D1 所示。相比DQN 结构，DDQN 结构的态势利导函数衰减速度更快，衰减过程中波动更小，说明DDQN 具有更优越的自学习能力。

3）学习率取值分析

学习率取值对比见附录D 图D2。当学习率α为0.007 时，态势利导函数收敛最快且收敛值最小，即此时DRL 算法训练效果相对较优。

4.3 优选群组及优化策略分析

数据采样间隔为15 min 的情况下，各CCR 群组的计算值箱形图如图3 所示，N5 群组计算值最大，即为优选群组，该计算值对应的节点响应状态即为最优状态响应空间。

图3 N1 至N8 群组计算值箱形图Fig.3 Box-plot of calculated values for groups N1 to N8

针对N5 群组基于DQN 和DDQN 的最优响应状态空间（a(13)t，a(16)t，a(29)t，a(31)t）见表1。相对于基于DQN 的最优决策，基于DDQN 的最优决策累计停电次数更小。最优响应状态下N5 群组节点核定削减负荷功率曲线如图4 所示。

图4 最优响应状态下N5 群组节点核定削减负荷功率曲线Fig.4 Approved load reduction power curve of group N5 nodes in optimal response state

表1 基于DQN 和DDQN 的最优响应状态空间Table 1 Optimal response state space based on DDQN and DQN

不同策略下的节点电压标幺值如表2 所示，节点17、32 的电压经过基于DDQN 和DQN 的DRL 算法训练优化CCR 群组节点的动作后，情况明显得到改善。

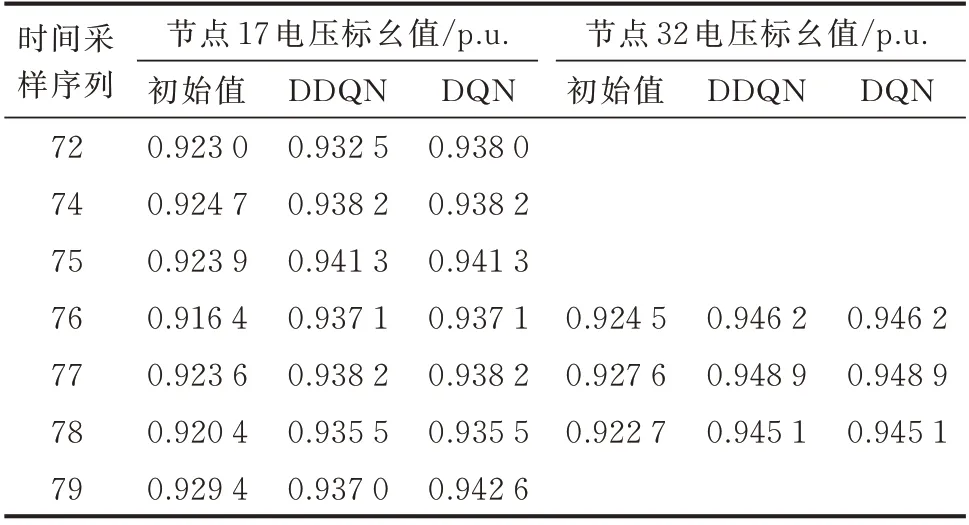
表2 不同策略下的节点电压标幺值Table 2 Per unit value of node voltage with different strategies

供电公司在CCR 群组节点的售电利润以及单组CCR 的补偿见表3。相对基于DQN 的最优决策结果，基于DDQN 的最优决策CCR 群组节点停电次数较少，改善了电压运行状态的同时，增大了供电公司的利润，减小了补偿费用。

表3 供电公司的售电利润以及CCR 补偿费用Table 3 Electricity sale profit of power supply company and CCR compensation cost

采样间隔为30 min 时，针对N5 群组基于DDQN 的最优响应状态空间（a(13)t，a(16)t，a(29)t，a(31)t）见表4，节点电压标幺值如表5 所示。由表4 和表5 可以看出，数据样本减少时策略仍然有效。

表4 基于DDQN 的最优响应状态空间(30 min 采样间隔)Table 4 Optimal response state space based on DDQN(sampling interval of 30 min)

表5 节点电压标幺值(30 min 采样间隔)Table 5 Per unit value of node voltage(sampling interval of 30 min)

5 结语

本文提出基于态势利导的需求响应自学习优化调度方法，实现了多随机场景下CCR 群组的优选及对应节点的优化调度。主要工作如下：

1）针对需求响应的显著不确定性，本文基于MDP 将其数学模型映射至态势感知元组，利用DRL 算法自适应用户行为和电网运行状态的不确定性。

2）自学习智能体基于态势利导函数，通过环境理解函数的激励与惩罚实现决策优劣的训练学习，针对不同数量的数据样本实现了自趋优决策。

3）本文设置负荷数据曲线泛化机制、ε-greedy贪婪策略和经验池机制，针对多随机场景不同样本，分别在DQN 和DDQN 架构下开展自学习，验证了所提机制在随机复杂场景下的性能优越。

在双碳战略背景下，本文方法可为平抑规模化接入分布式能源带来的强随机性提供参考，下一步将深入开展用户侧可再生能源发电的随机性建模，探索新型电力系统需求侧响应随机优化运行的调度策略，为中国新型电力系统供需平衡、安全稳定运行提供技术保障。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。