一种基于彩票迁移的稀疏网络植株病虫害识别模型
2022-12-13陈志奎李秋岑
张 旭,陈志奎,李秋岑,李 朋,高 静
(大连理工大学 软件学院,辽宁 大连 116620)
植株病虫害的识别是农业生产中一项重要的工作,需要及时准确地对病害状况进行检测,从而采取有效的防治措施。传统方法依赖经验进行人工观察和鉴定,准确率和效率都不尽人意[1]。应用计算机技术对病虫害进行自动识别,是实现智慧种植中不可或缺的一环。早期方法基于机器学习的分类方法,在小规模数据集上效果较好。近年来,伴随着农业大数据化,数据量不断升级,加上深度学习的高速发展,使用深度神经网络进行病虫害图像识别在国内外都取得了一定的成果:文献[2-4]分别使用采集的病态和健康的植物叶片训练卷积神经网络,得到的网络识别精度高,分类效果明显。文献[5]使用基于深度卷积神经网络(CNN,convolutional neural networks)的模型对水稻病叶进行识别,精度达到了95. 48%,高于传统的机器学习模式。文献[6]使用faster R-CNN识别茶叶的褐斑病、水疱病等病变。文献[7]使用GoogleLeNet建模水稻穗株的高光谱图像,对病株进行识别。文献[8]综合多种深度神经网络的特征提取器提出一种深度学习元体系结构,实现了对番茄病变的实时监测。然而,这些基于深度神经网络的方法在提供优秀的性能同时,往往需要依靠大量的有标签数据样本进行训练,数据则需要专业人员进行采集和标注,带来了高昂的训练成本,一定程度上限制了方法在实际问题中的应用。
为了减少实际应用中的数据需求和标注成本,深度迁移学习(deep transfer learning)是经常被选择的方案,这一思路也已经被扩展到病虫害识别工作中。文献[9]应用迁移学习方法训练深度卷积神经网络,进行木薯病虫害识别,在取得高识别精度的同时减少了训练开销。深度迁移学习可以将知识从源域迁移到目标域,将多任务中共享的知识进行复用,并根据目标任务更新学习模型,和人类的认知策略类似[10]。在计算机视觉领域,卷积网络提取的浅层视觉特征在多任务中往往可以复用,该理论已经得到证明[11]。因此,通过复用在海量数据集和高性能硬件设备预训练模型的一部分,用于完成实际任务中的特征提取等工作,可以大幅减少所需的有标签数据量,缩短训练时间,从而减少训练的开销。然而,迁移学习仍然无法解决需要训练网络中海量参数的问题。先进的卷积神经网络的一个发展趋势是,为了获得更高的精度,需要训练更大和更深的网络,从而带来更加高昂的内存和计算开销。一个简单的ResNet-18(具有18个卷积层的残差卷积神经网络)在每一轮训练过程中就有多达10.9 M(million)个参数需要训练,需要进行的浮点数运算(FLOP)次数多,对硬件设备要求高。这限制了深度学习方法应用于移动终端、低算力的边缘计算设备等领域的可能性。
剪枝(pruning)是常用的削减卷积神经网络体量的方法之一[12-13]。虽然神经网络的性能和参数数量有关,但并非所有的分支和对应的参数都做出相同贡献,很多训练完成的深度神经网络是过参数的[14]。通过对冗余的参数进行修剪,可以在只保留部分重要网络结构的前提下保证准确率。已有少数工作把迁移和剪枝结合起来,以进一步减少开销和缩减网络体量[15-16]。2019年,Frankle 和 Carbin提出了彩票假设(lottery ticket hypothesis)[17],该方法可以寻找原始网络中最富代表性的子网络、该稀疏子网络重新训练后可以达到和原始任务相当的性能同时,最少可以仅保留原始参数量的5%~10%,这为迁移学习带来了新的方向。显而易见的,既然所有的网络权重并非做出相等的贡献,如果能够只迁移那些最重要的部分,就能大幅压缩需要训练的网络结构,从而实现一个准确率高而且更加精炼的可迁移稀疏子网络结构。节省开销的同时,使得任务更容易扩展到边缘计算等新兴领域,更容易适应实际生产和应用中的需求。
基于彩票假设,提出了一种稀疏子网络迁移学习,并尝试应用其解决植株病虫害图像识别的实际问题。首先,提出稀疏彩票迁移假设,将彩票假设扩展到深度迁移学习中,验证可以找到这样可迁移的稀疏子网络结构,在标准数据集上验证可迁移性;随后,应用植株病虫害数据集,对稀疏网络进行训练,探索在实际问题上的应用;最后,通过实验验证,使用该方法进行训练的网络在保留迁移学习对现有知识利用的优势同时,可以使用更加精简的网络架构和更少的参数完成相当(甚至更高的)的识别准确率。
1 彩票假设
彩票假设(lottery ticket hypothesis)于2019年由Frankle和Carbin提出。其内容是:对于一个前馈神经网络,存在一个隐含的、可以重新训练的最优稀疏子网络结构,仅通过从零开始重新训练该稀疏子网络即可获得和原始稠密网络相同的精确度,且迭代次数不超过原始网络。该子网络在整个网络被随机初始化时产生,并且可以简单地由非结构化剪枝算法得到。Frankle和Carbin在最初的研究中发现,只有当使用原始网络的初始化参数重新训练时,该子网络才能获得更好的性能,用新的权重进行随机初始化则会导致效果不佳。换言之,剪枝的特定组合在原始网络中找到了一个幸运的被初始化成最佳形态的子网络,该子网络因此被命名为“彩票子网络”。原作者讨论了彩票子网络是否与所训练的任务结构相关,以及得到的子网络是否总是能够在任务之间进行迁移,目前还没有定论。笔者讨论并验证该假设在图像分类任务中不同数据集间迁移的可行性,探索彩票假设在迁移学习中的应用。
原始彩票假设的形式化定义如下:对于一个神经网络f(x;θ),定义其初始化参数为θi。在网络的训练优化过程中,经过j次迭代,f取得最低的代价函数损失l,此时网络在当前任务上达到α%的准确率。存在这样的子网络f(x;m⊙θi),m∈{0,1},当其代价函数最低时,满足迭代次数j′≤j且准确率α′≥α,称这样的网络为一个彩票子网络。
所有的彩票子网络都可以通过非结构化剪枝得到,并且可以重新训练。当使用原始网络的参数θi进行训练时,子网络的性能好于随机初始化[17]。
2 基于彩票剪枝的稀疏子网络迁移方法
基于彩票剪枝的稀疏子网络迁移方法,该方法在应用彩票假设寻找可训练稀疏子网络的基础上,将方法扩展到深度迁移学习,寻找一个可迁移的稀疏子网络,保留源域的重要信息并应用其协助目标域训练。首先,在源域上应用彩票假设,寻找最优化的彩票子网络结构;再将该网络迁移至目标域,尝试仅使用目标任务中的少量有标签数据对网络进行微调,使之达到最优。另外,在原始彩票剪枝算法的基础上进行改进,包括优化其剪枝标准和子网络的训练方法,从而进一步提高最终得到网络的精度。
2.1 稀疏彩票子网络可迁移假设
深度迁移学习经常应用于将知识从源域迁移到目标域,复用共享的知识并且根据目标任务更新学习模型。其中,“域”定义为:D={χ,P(X)},包括特征空间χ以及边缘分布概率分布P(X),X={x1,…,xn}∈χ;“任务”定义为T={y,f(x)},其中y代表标签空间,f(x)代表用于标签预测的目标函数。在基于深度神经网络的任务中,可以用来反映神经网络的非线性损失函数。原始的彩票假设仅在当前的目标任务域DT上进行。本方法结合深度迁移学习,使用来自源域的信息辅助目标域,从而同时大幅削减训练所需的有标签数据集和参数数量两方面的开销,完成一个稀疏子网络的迁移。因此,对于目标域DT上的待解决的目标任务TT,从选定的相对较大的源域DS上的现有任务TS寻求帮助,使用2个域的共同知识优化目标域的损失函数fT(x)。综上所述,在基于彩票假设的迁移方法中,需要完成对目标任务(DS,TS,DT,TT,f(x;m⊙θi),m∈{0,1})的最优化工作。
给出稀疏彩票迁移假设的形式化定义:
使用神经网络f(x;θ)定义目标域DT上的任务TT。在使用来自DT信息进行训练优化的过程中,经过j次迭代,f取得最低的代价函数损失l,此时网络达到α%的准确率。定义源域DS的初始化参数为θs。存在这样的子网络f(x;m⊙θs),m∈{0,1},通过在源域任务TS上应用彩票假设剪枝得到,当其代价函数最低时,在DT上仍能满足迭代次数j′≤j且最终准确率α′≥α。称这样的网络为一个可以从源域迁移信息到目标域的稀疏彩票子网络。
2.2 基于彩票假设的稀疏子网络迁移
改进的基于彩票假设的稀疏子网络迁移方法,其实施步骤如图1所示。
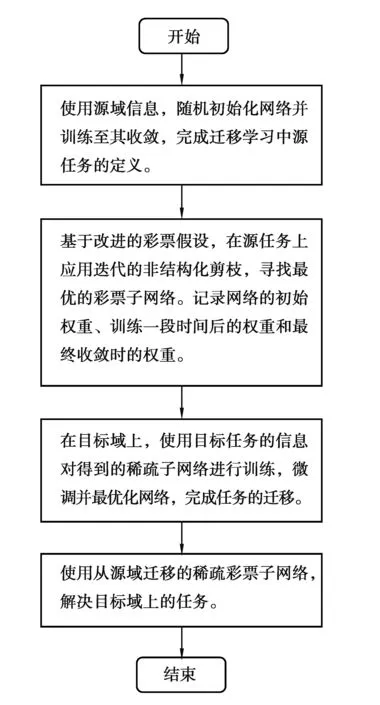
图1 基于彩票假设的稀疏子网络迁移过程Fig.1 Process of lottery ticket-based sparse neural network transfer
首先,随机初始化网络参数θ。在使用非结构化剪枝方法寻找彩票子网络的过程中,为所有的参数约定一个初始化掩膜m(mask)和对应的掩膜标准M,用于判断并标记剪枝操作后哪些权重将被保留。因此,可以将即将被迁移的原始网络定义为f(x;m⊙θ)。
方法的具体实现步骤如下:
步骤1:在源域上随机初始化网络,并且使用源域信息进行训练直至其收敛,完成源任务的定义。该步骤尝试通过对现有任务部分关键网络结构和对应权重的复用实现知识迁移。因此当源任务为其他领域已经完成的工作,或者使用该领域富有代表性的海量通用数据集在高性能硬件设备上训练而来的已知网络(ImageNet上训练的高质量图像数据集)时,可以省略训练步骤,直接继承源任务的权重和结构。
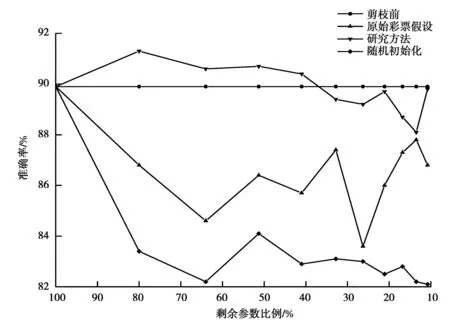
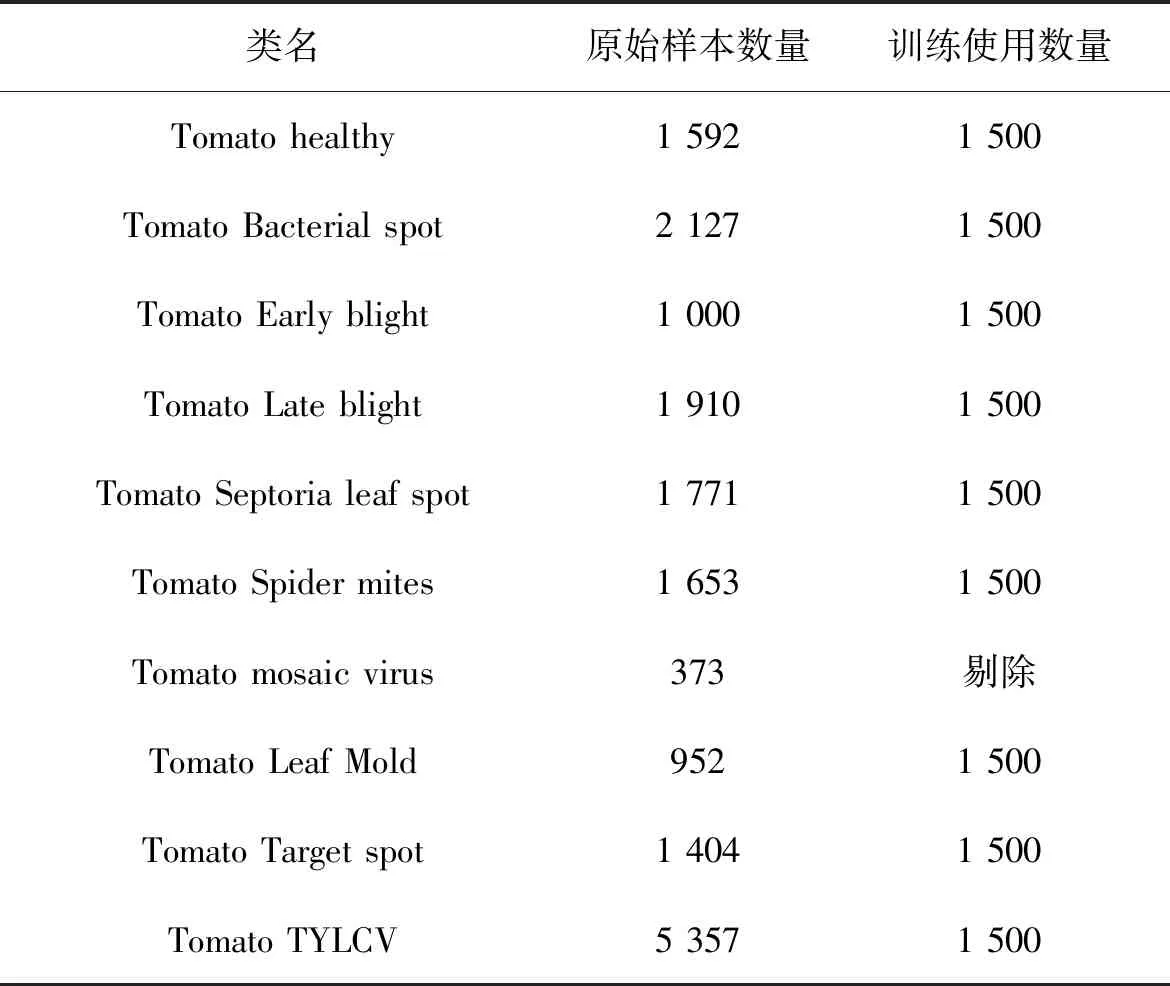
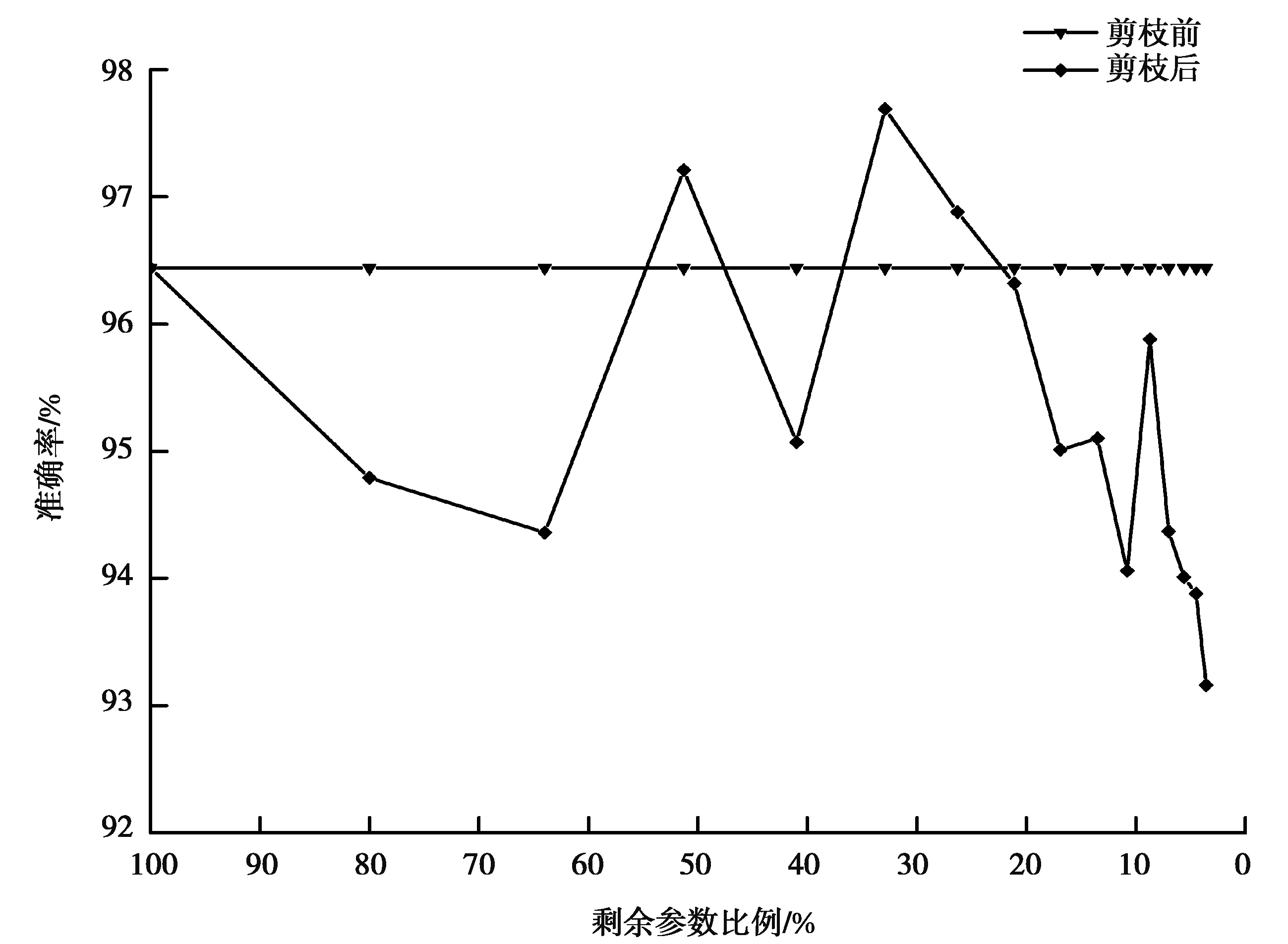
步骤2:基于改进后的彩票剪枝方法,在该网络上应用迭代的非结构化剪枝算法,以寻找最优的彩票子网络。对于经历n次迭代的网络,记录训练前的初始权重,表示为θi;训练完成后的权重表示为θn。此外,记录训练开始后一段时间的权重,表示为θj(j 步骤3:在彩票剪枝算法运行过程中,使用掩膜标准M对网络中的每个权重进行判断。M可以视为对权重在神经网络中贡献度的打分标准,其定义如下 在网络的每一层中,对于得分在前p%的权重,设置其掩膜m=1,表示将被保留;对于剩余的(100-p)%权重,其掩膜m将被设置为0,表示被剪去,并随机破坏其连接。p代表保留权重的比例,将会影响剪枝的程度,可以根据具体的层数不同进行分别定义。 步骤4:对于m=1的权重,使用θj重置其权重,准备进行下一步的训练;m=0的权重将被剪枝,这些被剪掉的权重在后续的训练中将被冻结(不参与训练)。与原始的彩票剪枝方法有所区别的是,只有当即将被剪枝的权重在训练中的趋势是趋近0时,将其冻结为0;如果其趋势是逐渐远离0,则将其冻结为初始权重。 步骤5:重复1—4的步骤,直到在源域上找到最优的可迁移稀疏彩票子网络f(x;m⊙θi)。 步骤6:在目标域上,使用目标任务的数据集对得到的子网络进行微调训练,完成网络的最优化,从而完成迁移任务。在训练时,使用θj初始化网络中被保留的权重,被冻结的权重不参与训练。 此时得到的稀疏网络继承了来自源域的信息,并且能够用于目标域任务,且需要训练的参数和训练用的真实数据集数量大幅减少。 相比原始的彩票假设,为了将其应用于迁移任务并且优化其性能,在如下方面进行改进: 1)原始的彩票假设仅能用于当前域。则当在目标任务域上应用彩票剪枝时,按照原始的彩票假设,应该使用目标任务上的初始权重作为子网络的初始权重(而非随机初始化网络)进行训练,得到的子网络才能尽快收敛并达到剪枝之前准确率的水平。但在深度迁移学习中,显而易见的,如果使用目标任务上的初始权重,源域获得的知识将会丢失,相当于使用一个随机值开始训练,使源域上的训练没有意义。因此,为了从源域迁移现有的知识,本方法使用源域训练得到的权重对子网络进行初始化并应用于目标任务,实现彩票网络的迁移。 3)在原始彩票假设的剪枝方法中,在剪枝结束后,将会使用剪枝开始前的初始权重θi对被保留的权重进行初始化。后续研究发现,使用训练一段时间后的权重θj(j 4)在原始彩票假设的剪枝方法中,和其他的剪枝方法类似,被剪枝的权重在后续的训练中将被一概冻结为0。一般认为可以这么做的理由是这些权重在网络中贡献较少,属于不重要的分支。这些权重应该可以被设定成任意值——而不是特定的0值——而不会影响网络的最终效果。实验中发现,和晚重置方法类似,通过剪枝方法将特定权重冻结之所以有效,是因为它们在一定程度上反映了权重在训练中的变化趋势。冻结为0的操作约等于令那些随着训练会越来越接近0的权重提前达到其近似的最终值。因此,在本文方法中,只有当一个权重的变化趋势是趋近0时,将其冻结为0;当其在训练中的变化趋势是不断远离0时,将其冻结为初始的值。 首先使用标准数据集,对提出的稀疏彩票子网络可迁移假设进行验证。对源域上的任务进行剪枝,找到最优彩票子网络后,在目标域的数据集上应用该子网络,与直接在目标数据集上训练完整网络得到的结果相比较,分别对比平均准确率(ACC, accuracy)和需要训练的参数数量,以检验该假设是否成立。 选择多类别图像分类问题,使用CIFAR-10[19]训练迁移任务的源域。CIFAR-10是一个被广泛使用的标准数据集,用于识别普适物体,常作为基准对各种模型进行有效性检验。目标数据集选择smallNORB[20],它是LeCun等人拍摄的不同照明及摆放方式下的玩具模型灰度图像的小尺寸版本,常用于对3D生成模型进行测试。数据集的具体属性如表1所示。由于目标域上的图像尺寸和通道与源域不同,在实验中,使用4单位的像素填充/裁剪,并且进行通道转换。 表1 数据集属性Table 1 Properties of datasets 网络架构方面,选择ResNet18模型。这是经典深度残差网络ResNet架构的18层版本,也被Frankle等应用于验证原始的彩票假设,使用和作者相同的配置[17]。其原始版本有多达10.9M(million)个卷积层参数需要训练。在剪枝过程中,只对卷积层进行操作。在目标域上对迁移的子网络微调使之最优化时,按照迁移学习中常用的方法,冻结卷积层的权重,只微调全连接层。实验使用3种不同的初始化方式初始化彩票子网络:晚重置方法,原始彩票假设中的方法,以及随机初始化。 实验中的其他参数设定如下:应用随机梯度下降(SGD)进行优化,参数(5e-3,1e-3,1e-4);基础学习率0.01;动量参数momentum=0.9;权值衰减率decay=1e-4。在每一轮剪枝中,剪掉当前参数的20%,总共进行10轮迭代剪枝,批处理大小为128,最大迭代次数为30 000,每轮中最多进行50次遍历。实验全部在Dell PowerEdge R740(Silver 4110 2.1 GHz-8cores-16threads*2 NVIDIA Tesla M60*2 128G)服务器上运行。 经过在源域CIFAR-10上的训练后,网络在测试集上取得89.43%的准确率。彩票剪枝可以在保证准确率的前提下大幅削减所需训练的参数数量,剪枝后只保留原始参数的10%时,仍具有89.24%的准确率。对于目标域数据smallNORB,当从头训练同样的稠密网络时,准确率为89.9%。为了寻找最适合迁移的稀疏子网络大小,将不同剪枝程度下每一轮产生的最优子网络分别迁移至目标域,按照研究提出的稀疏彩票迁移假设进行训练,并对结果进行对比。 实验结果如图2所示。 图2 彩票迁移在标准数据集上的结果Fig. 2 experimental results of lottery ticket-based transfer on benchmark datasets 可以发现,对源域剪枝得到的稀疏网络可以用于目标任务。在大幅节省参数训练开销的同时,总体精度能保持在剪枝前附近,实现了稀疏子网络的迁移。并且当进行适当剪枝时,可以取得比直接训练稠密网络更好的性能。相比原始彩票假设中的初始化方法和随机初始化方法,改进的方法能更有效实现稀疏子网络的迁移。 在实际应用中,可以进行更细粒度的剪枝,以逐步寻找用于迁移的最优稀疏网络。同时,实验结果表明,当进行深度剪枝,即仅保留原始网络10%参数时,其精度损失也可以接受。当目标任务可以接受性能的微弱损失时,这为深度计算方法在移动智能设备或者低算力的边缘计算设备上的推广提供了可能性。总体而言,通过在标准数据集上的实验,验证了提出的稀疏彩票可迁移假设的可行性。 应用稀疏彩票迁移假设训练一个稀疏子网络,用于解决植株病虫害的识别问题。具体的,对番茄叶片的常见病害进行识别。使用在ImageNet上预训练完成的ResNet18模型作为源域网络,进行15轮迭代剪枝,最少可以仅保留原始参数的3.6%。其它参数和实验设备设置与上一节相同。在目标域上,使用PlantVillage数据集进行训练。PlantVillage数据集是PlantVillage网站(https:∥www.plantvillage.org/en/plant_images)收集的14种农作物、26类植株病虫害的叶片(及其对应的健康叶片)组成的开源图像数据集。由于原始数据集中不同类别的样本参差不齐,只选择Tomato类,剔除样本较少的类和质量较差的图片,再使用水平翻转等数据增强手段,将每类的样本大小调整到基本一致,共定义8类病害+1类健康叶片。同时,图像大小统一调整为64×64。数据集的具体属性如表2所示。 表2 PlantVillage数据集属性Table 2 Properties of PlantVillage dataset 实验结果如图3所示。原始稠密网络经过训练,可以达到96.44%的准确率。通过应用稀疏彩票迁移假设,分别获得了一系列体量不同的稀疏子网络,识别准确率最高可达97.69%,同时所需训练的参数数量大幅减少。在仅保留3.6%参数时,仍可以达到93.16%的准确率,为深度学习方法在低算力设备上的应用提供了可能性,此时只需要训练406 495个参数(相比原始网络的11 173 962个);当需要最佳性能时,可以在最高准确率附近通过更细粒度的剪枝进一步寻找最优子网络,此时所需训练的参数可能只有原始网络的20%~50%,同时准确率高于原始稠密网络。 图3 稀疏彩票迁移训练子网络Fig. 3 Experimental results of lottery ticket-based transfer on Plant Village dataset 研究提出一种基于彩票假设的稀疏子网络迁移方法,在借助源域知识迁移以减少训练对有标签数据样本需求的同时,可以大幅减少需要训练的参数数量并保持网络精度,实现更加精简高效的深度迁移学习。在标准数据集上验证了应用彩票假设剪枝得到的稀疏子网络可迁移的假设。进一步应用该方法训练一个稀疏的深度网络,进行番茄叶片病害的植株病虫害识别工作,识别准确率可达97.69%,且只需要训练原始参数的30%。 研究仅验证了方法在ResNet网络结构上的可能性。该假设能否有效应用于其他网络结构,以及扩展到目标分类以外的任务,将是下一步的研究方向。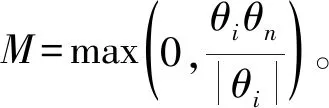
3 实验及分析
3.1 稀疏彩票迁移假设的验证

3.2 基于稀疏彩票迁移假设的植株病虫害识别方法
4 结 论
