基于修正系数法的桩基水平静载试验参数分析

郝文亮，杨小龙，张天宇，刘怡嘉

(1.内蒙古电力（集团）有限责任公司鄂尔多斯供电分公司，内蒙古 鄂尔多斯 017000；2.内蒙古大学交通学院，内蒙古 呼和浩特 750306)

0 引言

桩基础由于具有承载力高、稳定性好、沉降量小等特点，在电力、公路、铁路、市政、房建等各类工程建设中得到了广泛应用。对于承受水平荷载下的重要结构物或地质条件复杂的桩基工程，为了验证设计计算模型或参数选取的合理性、数值模拟结果的正确性以及检验施工质量等，水平静载试验是一种常用的方法。目前，通过水平静载试验获取相关的地基模型参数常用的分析方法有m法[1-3]，双参数法[4]，p-y曲线法[5-7]等。m法根据桩在地面处的实测位移推算地基系数的比例系数m值，由于参数单一导致地面处的位移、转角、桩身最大弯矩等理论值不能很好地与实测值相符。双参数法通过调整参数α和1/n两个参数，使得桩在地面处的位移、转角、桩身最大弯矩及其位置等指标理论值同时与实测值相符，结果比较满意。p-y曲线法通过数学方法对实测弯矩数值进行曲线拟合或光滑处理，求得了与实测弯矩非常接近的弯矩曲线。通过对弯矩曲线求二阶微分和二阶导数，从而求得p-y曲线。该法计算精度高、结果可靠。

相对而言，m法参数选取方法简单，在工程中应用较为广泛。该法基于Winkler地基模型假定地基为非连续介质，忽略了地基土体的抗剪能力。文献[8-9]通过Pasternak双参数地基模型分析了土体剪切刚度对横向受荷桩桩顶位移和桩身最大弯矩的影响。研究结果表明，随着土体剪切刚度的增大，桩顶位移和桩身最大弯矩均不同程度地减小。针对m法在桩基水平静载试验参数分析中存在的不足之处，本文提出了一种修正方法，为m法试桩资料参数分析提供参考。

1 参数敏感性分析

为了研究桩土相对刚度α变化对桩身位移、弯矩和转角的影响，取地面处位移x0、转角φ0、最大弯矩Mmax作为分析参数。由m法计算式，得：

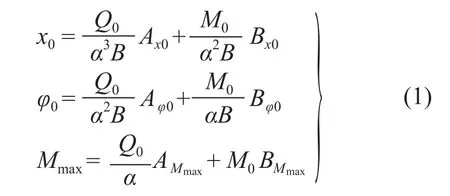
式中：Q0、M0为地面处的荷载；B为桩的抗弯刚度；Ax0，Bx0，Aφ0，Bφ0，AMmax，BMmax分别为位移、弯矩和转角系数。

当仅考虑剪力作用时，由式(1)三个参数对α求导，得：

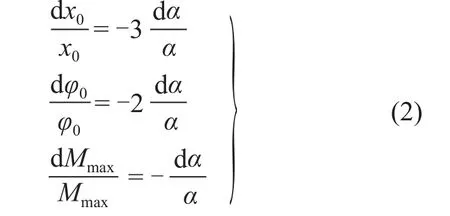
当仅考虑弯矩作用时，同理可求得：

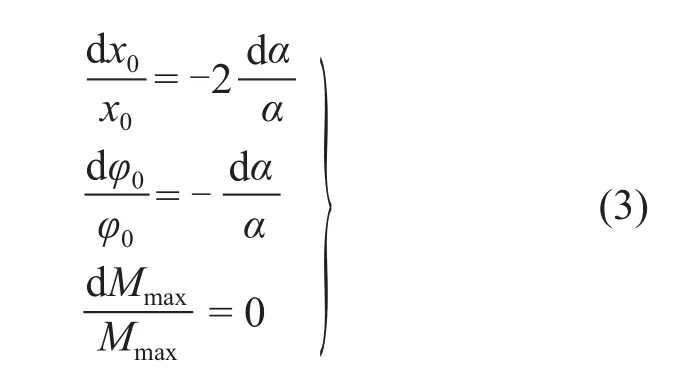
由以上分析可知，桩土相对刚度α变化对地面处位移x0影响最为敏感，依次为转角φ0、最大弯矩Mmax，且剪力作用下对其影响大于弯矩。

实际工程中的地基并非理想的Winkler地基。m法忽略了桩土之间的摩擦力、粘结力以及地基土体的剪切作用，导致计算结果偏大。桩基水平静载试验参数分析时，通过地面处位移实测值等于理论值这一条件推算α和m值，实质上相当于增大了α的取值，从而不同程度地影响转角和弯矩的计算结果，导致理论值与实测值误差变大。

2 修正系数法

小变形条件下水平静载试验参数分析常用的方法是m法，采用地面处位移实测值计算桩土相对刚度α和水平向地基系数比例系数m值。该法桩的抗弯刚度取理论值，实质上相当于指定的其中一个参数。大量静载试验成果表明，m法计算的地面处的位移、转角、桩身最大弯矩等理论值不能同时满足与实测值相等的条件。

吴恒立[4]提出的综合刚度原理和双参数法对m法做了改进。该法将桩身抗弯刚度视为待定参数，用桩土综合刚度描述。采用地面处位移和转角实测值计算桩土相对刚度α和桩土综合刚度，通过调整地面附近的土抗力保证桩身最大弯矩计算值与实测值相符。

长期以来，人们仍习惯于采用桩本身的抗弯刚度分析横向受荷桩的受力性状。为了提高m法的计算分析精度，本文在上述两种方法的基础上提出了如下修正系数法：

1)假定桩土综合刚度为B0，桩土相对刚度为α0。采用地面处位移和转角实测值联立求解α0和B0。由式(1)得：

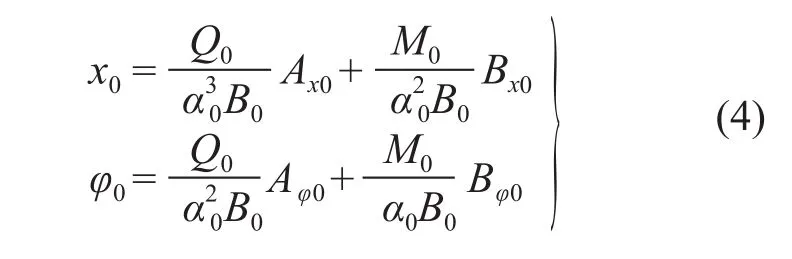
式中：x0、φ0分别为地面处位移和转角实测值。

令M0= e0Q0，式(4)整理后得：

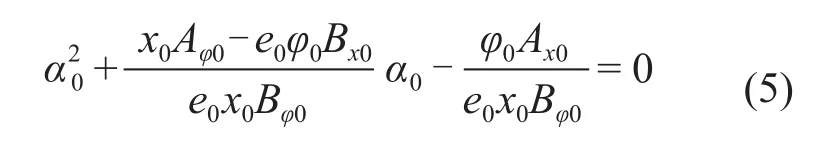
解上述方程可求得α0，代入式(4)求B0。

2)令k = B0/B，由式(4)得：

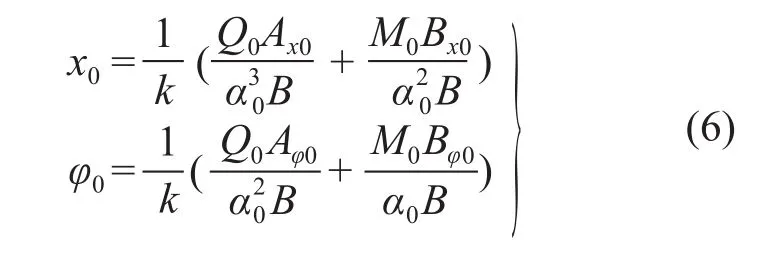
式中：B为桩的理论抗弯刚度。

式(6)即为桩的抗弯刚度取理论值时，双参数模型的另一种形式。实质上是修正系数法的一种特殊形式，即桩土参数取α0、B时，采用统一的修正系数1/k对荷载作用下的变形值做修正，保证了桩在地面处的位移、转角计算值与实测值相符。

式(6)变形后，得：

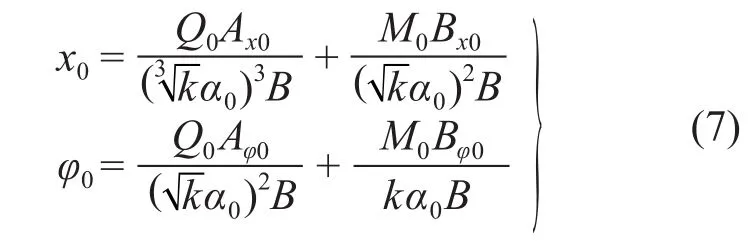
式(7)表明：当桩的抗弯刚度取理论值时，m法桩土相对刚度取同一值时地面处的位移、转角计算值不能满足与实测值相符这一条件。

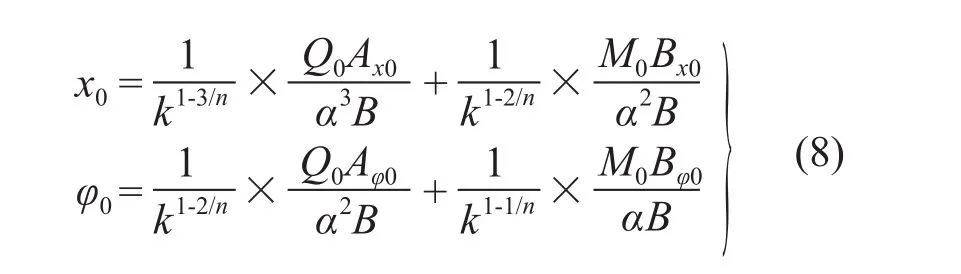
由式(8)可知，在m法的基础上，采用分项修正系数的计算模型能够保证桩在地面处的位移、转角计算值与实测值相符。改变桩土相对刚度α后，修正系数随之发生变化。采用不同的桩土相对刚度和修正系数均能够保证桩在地面处的位移、转角计算值与实测值相符。但桩土相对刚度究竟取何值时能够更好地反映桩土实际工作状况，需要结合桩身最大弯矩对比分析和评价。

相应的桩身弯矩公式可表示为：

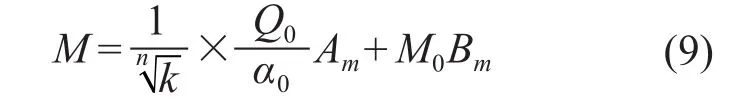
实际上，因为桩土相对刚度α变化对位移最为敏感且某些情况下桩的承载力往往由地面处的位移控制，α的合理取值范围应为：

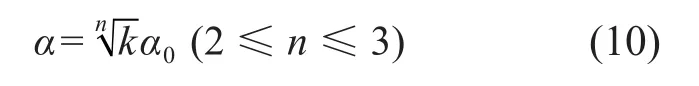
首先给定n的初始值，计算桩身最大弯矩并与实测值对比，通过调整n的大小即改变土抗力的大小使得桩身最大弯矩接近实测值，从而确定n的合理取值范围。

综上所述，本文方法计算过程为：①采用地面处位移和转角实测值联立求解桩土相对刚度α0和桩土综合刚度B0；②计算刚度修正系数k；③根据桩身最大弯矩确定n的取值，对α0做修正；④计算桩身最大弯矩并与实测值对比，验证计算模型的可行性。

3 模型验证

1)算例1

扶余松花江大桥Ⅳ#试桩资料[4]为：钻孔灌注桩，采用200号混凝土，直径D= 1.62 m，入土深度18.8 m，有钢筋骨架。桩身抗弯刚度理论值取0.67EcIc，n取2。根据地面处位移和转角实测值计算桩身最大弯矩，结果见表1所列。荷载Q0= 600 kN，弯矩M0=150 kN·m时，采用m法、本文方法和双参数计算理论弯矩，与实测值相比如图1所示。

图1 算例1桩身弯矩沿深度分布

表1 计算结果对比

由表1可知：①总体而言，每一级荷载作用下，本文方法计算的桩身最大弯矩误差较m法小；②前两级荷载作用下计算的弯矩误差较大，主要原因是本文方法仍假定地基系数沿深度线性分布且认为地面处土抗力等于0，通过改变α的取值调整土抗力的大小，参数单一，某些情况下效果有限，前两级荷载作用下计算的最大弯矩与m法相比误差虽然减小了约50%左右，但若想接近实测值需要改变地基系数模型，行之有效的方法是双参数法；③后两级荷载作用下计算的最大弯矩接近于实测值，分析参数k的取值后发现，当1≤k≤2时，本文方法计算的最大弯矩值误差很小。

2)算例2

镇江北固路6#桩试桩资料[4]为：钻孔灌注桩，采用25号混凝土，配筋率为0.54%。桩全长11.5 m，入土深度11.0 m，直径D = 1.04 m，桩头自由。桩身抗弯刚度理论值取0.67EcIc，n=2.5。根据地面处位移和转角实测值计算桩身最大弯矩，结果见表2所列。由表2可知，每一级荷载作用下，本文方法计算的桩身最大弯矩误差很小，相应的k值分别为1.27、1.37。

表2 计算结果对比

荷载Q0= 250 kN时，采用m法、本文方法和双参数计算理论弯矩，与实测值相比如图2所示。分析以上两个算例，由图1～图2可知，本文方法计算的最大弯矩理论值与双参数法和实测值基本接近，桩身弯矩沿深度分布较m法合理。与实测值相比，桩身下半部分本文方法弯矩计算值偏小，主要原因是m法假定地基系数随深度无限增长，导致地基系数偏大，与实际情况不符。与m法相比，采用修正系数法能够更好地模拟桩土的实际工况。

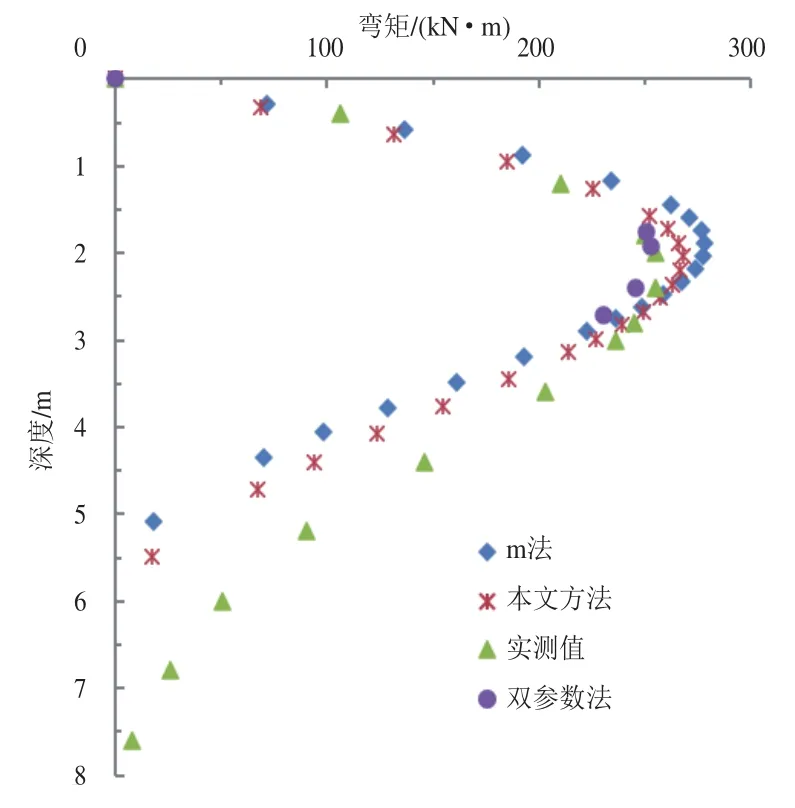
图2 算例2桩身弯矩沿深度分布

4 结论

1)考虑m法在桩基水平静载试验参数分析中存在的不足之处，提出了一种基于修正系数法的桩基水平静载试验参数分析方法。该法能够保证桩在地面处的位移和转角理论值与实测值相符。

2)桩身最大弯矩理论值较m法误差小且弯矩沿深度分布较m法合理，修正系数法能够更好地模拟桩土的实际工况。

3)基于算例计算结果，当桩土综合刚度与桩的理论抗弯刚度之比在1≤k≤2时，本文方法计算的最大弯矩值误差很小。