基于Hopfield神经网络的磁浮列车悬浮系统本征非线性特性辨识*

宋一锋 倪 菲 林国斌 陈 琛 刘永红 陶清宝

(1.同济大学道路与交通工程教育部重点实验室, 201804, 上海； 2.同济大学磁浮交通工程技术研究中心,201804, 上海； 3.茂盟工程技术股份有限公司, 203201, 上海∥第一作者， 硕士研究生)

如何保证磁浮列车在运行状态下的稳定性，是控制领域以及动力学领域研究的热点问题之一。一些学者对此展开了深入研究，在模型修正、动力学响应和控制算法等方面均取得了许多成果。

在模型修正方面，目前最为普遍的做法是将系统非线性项在平衡点处进行泰勒展开，在此基础上设计线性控制算法，但线性化处理使得模型丢失非线性项特性。此种情况下设计的控制算法，只能保证系统悬浮间隙在误差很小时快速收敛，当悬浮误差较大时，系统就极有可能发生失稳现象[1-3]。然而，实际物理系统均不可能是线性系统，因此相关学者通过非线性模型以及系统辨识来进一步靠近真实模型，以求能贴近真实情况，从而提高控制性能。文献[4]指出在线性化处理非线性模型时，会在一定程度上忽略某些非线性特征，从而产生系统偏差。文献[5]在研究PID(比例-积分-微分)控制时，提出神经网络结构可以用于优化多变量系统结构，进而进行非线性系统辨识，并通过实验验证了这一观点。文献[6]分析了均值定理对局部动态线性化的作用，并结合回归学习控制理论对非线性系统进行了建模和辨识。

由于磁浮列车在运行过程中，悬浮间隙仅为毫米级别，因此在非线性负载以及轨道微量变形的激励下，极易导致列车的失稳现象。在控制算法和动力学响应方面，文献[7]提出了一种磁浮列车悬浮系统的模糊系统和参数辨识算法，通过该算法辨识隶属函数的参数，便于快速响应系统变化。文献[8]建立了基于柔性轨道的车-轨耦合模型，将轨道视为简支梁，设计了基于RBF(径向基函数)网络逼近原理的滑模自适应控制器，用以提高系统控制性能。文献[9]引入粘弹性模型来描述动态力，基于高温超导磁悬浮系统的振动响应，采用最小二乘法辨识模型中的参数，用以更好地反映高温超导磁悬浮系统的动态特性。文献[10]分析了磁浮列车运行过程中的车辆随机振动的激励源，采用伪激励法对激励计算量进行了有效简化。

本文建立了基于柔性轨道的磁浮车-轨耦合系统模型，并分析Hopfield神经网络结构的相关性理论。由于车-轨耦合动力学模型在输入、输出的映射关系上表现为本征非线性，且在时域上可以假设为均匀采样，因此通过对所采集信号进行误差函数设计以及网络信号分析，可获取估计结果。为了提高模型精度并降低复杂度，采用参数辨识误差函数和Hopfield神经网络的标准能量函数进行系统辨识，给出辨识表达式以及含参非线性项的相应辨识结果。由于辨识得到的模型相对非线性模型更为简单，且能够最大程度地保留系统的非线性特征，因此对于磁浮列车悬浮系统的悬浮稳定性分析具有重要意义。

1 基于柔性轨道的车-轨耦合模型构造

1.1 轨道结构竖向运动模型

为进行相应的模型辨识，建立基于柔性轨道的单点悬浮控制模型，如图1所示。其中，xc为当前悬浮间隙，xm为电磁铁竖向位移，xg为轨道竖向位移，m为恒定负载质量，FL为电磁铁产生的悬浮力，i为悬浮电流，N为电磁铁线圈匝数，A为电磁铁磁极面积，μ0为真空磁导率，R为电磁铁绕组电阻，O定义为笛卡尔坐标系原点。

由图1可知，由于磁浮列车运行轨道的支撑方式采用高架梁，可将其简化为简支梁进行分析，因此，梁上任意一点的竖向位移xg都满足欧拉梁的相关动力学方程[11-12]：

kgxg=p(y,t)

(1)

式中：

E——轨道梁的弹性模量；

I——梁的截面惯量；

T——梁变形时产生的张力；

ρ——梁的质量线密度；

kg——轨道梁产生弹性变形时的弹性常数；

p(y,t)——车辆通过时在轨道梁上的质量分布密度；

t——时间;

y——电磁铁质心在OY方向上的位移。

设轨道梁跨度为l，则梁的质量M为：

M=ρl

(2)

由于磁浮列车竖向振动的最大振幅所对应的频率主要分布在固定范围内，且轨道结构相对固定，这种情况可以看作轨道的一阶振动频率[13]。

因此，可得到1阶模态下柔性轨道竖向位移的数学模型[14]为：

(3)

式中：

q1(t)——轨道梁一阶模态对应的广义坐标；

η1——1阶模态的阻尼比。

1.2 悬浮电磁铁竖向运动模型

在柔性轨道的作用下，悬浮间隙由电磁铁竖向位移和轨道竖向位移共同决定。因此悬浮间隙xc满足如下关系：

xc=xm-xg

(4)

电磁铁产生的悬浮力可以表示为：

(5)

根据牛顿第二定律以及图1所示的力的作用原理，可以得到：

(6)

在平衡点(i0,x0)处，电磁力和重力正好等价反向，合力为0，有：

(7)

根据电学方程的相关推导[10]，可以得到相应电压u方程：

(8)

1.3 车-轨耦合系统竖向运动模型

结合上述轨道结构竖向运动模型以及电磁铁竖向运动模型，可得到基于柔性轨道的一阶振型的车-轨耦合模型：

(9)

式中：

(2/M)sin2((πy0)/l)——量纲一化振型函数在该位置幅值的平方。

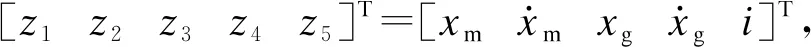
(10)

2 辨识模型方案设计

2.1 Hopfield网络在柔性轨道的磁浮车-轨耦合系统的应用原理

Hopfield神经网络模型本质上是一种反馈型神经网络。它由一系列互联的神经单元构成，以电学思路分析其结构，可通过图2进行相应描述。

图2中，ui为第i个神经元的状态输入，Hi为第i个神经元输入，vi为第i个神经元输出，wij为第i个神经元到第j个神经元的连接权值。此外，vi和ui之间存在非线性关系。

选取双曲函数g(x)描述vi和ui之间的非线性函数关系，即：

(11)

vi=g(ui)

(12)

式中：

φ、λ——神经元函数影响因子，取值均大于0。

对于基于柔性轨道的车-轨耦合系统而言，需要在状态空间内讨论Hopfield神经网络的动态特性，因此根据式(10)定义如下变量：

根据上述变量以及Hopfield神经网络的动态特性定义能量函数来描述其动态稳定性：

(13)

式中：

Ri——神经网络输入端电路电阻值；

bj——神经网络偏置，通常为常数。

定义W为权值矩阵，当其为对称矩阵时，对能量函数求导满足如下关系：

(14)

根据式(14)可以得到：

(15)

其中，Δ为极小正数，式(14)可描述为：

(16)

其中，vi=g(ui)，即可得到：

(17)

由于Ci为大于0的常数，且双曲函数单调递增，g-1(vi)>0恒成立，此时可以判断EN具有负梯度，此外，当且仅当dvi/dt=0时，存在dEN/dt=0。因此可以判断随着t的增加，Hopfield网络在空间中的解向着负梯度方向运动，最终输出的V为平衡点，此时EN达到最小值。

2.2 误差函数设计

(18)

式(18)中：z和u线性无关，同时由于zp为z的辨识输出，因此zp和u同样满足线性无关。

(19)

将式(18)代入式(19)可以得到：

(Az-Fzp+(B-G)u)

(20)

为了重点分析z和zp之间的拟合关系，而G→B，并且z和zp输出为10-3级及更小，对其矩阵进行装置相乘后可视为0。

uT(B-G)TFzp)

(21)

2.3 Hopfield网络设计

Hopfield网络能量函数趋于极小的过程，就是估计矩阵G和F收敛于实际矩阵A和B的过程。

第i个神经元的动态微分方程为：

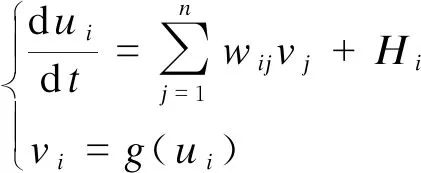
(22)

其中，g(ui)可以采用式(11)进行相关描述。

Hopfield网络的标准能量函数为：

(23)

式(23)中，Ri→∞，因此可以简化为：

(24)

对比式(21)和式(24)，并且将式(10)代入进行计算可以得到相应的网络权值矩阵W。将其代入式(22)即可得到稳定的ui，通过式(11)可以得到最终辨识结果输出为：

V=g(u)

(25)

3 数值仿真分析

对式(10)所示系统进行辨识，该系统状态方程如式(10)所示。

根据式(10)定义系数矩阵：

(26)

系数矩阵中各个元素如表1所示。

表1 系数矩阵中元素与变量对应关系

为了贴合实际磁浮车辆，本文采用低速磁浮车辆系统的真实参数进行数值仿真。柔性轨道情况下的车-轨耦合物理参数见表2。

表2 柔性轨道情况下的车-轨耦合物理参数

对式(26)中各个元素在平衡点处进行局部线性化，并代入数据可以得到：

A=

(27)

而系数矩阵中存在非线性项，且由z1,z3,z5状态变量构成，三者均为时变函数，因此A和B均可以看作时变系数矩阵。此时为便于分析，假定给予输入信号为正弦信号，并且设辨识结果V为：

V=[a11a12…a54a55b11…b15]

(28)

对比式(21)和式(24)，可以得到式(10)所示系统适用的网络权值。取双曲函数相关参数ρ=800，λ=5，表1中各个参数的辨识结果及辨识误差如图3—图8所示。其中：部分图中的分图展示了辨识结果达到稳态后的波动细节，水平线代表非线性项计算结果，波动曲线代表基于Hopfield神经网络的参数辨识结果，辨识误差指二者的偏差。

由图3—图8可看到，由于含参非线性项的存在，无法完全拟合线性化后的状态方程，此时可将辨识误差表征为非线性项在各个参数中的影响。如图3所示，辨识所得到的系统参数在5 s左右趋于平稳，此时辨识结果在[1.26,1.29]内波动，并且处于逐步减小的趋势。而参数最小的非线性项a45始终处于相对稳定的状态，非线性项仅仅会在某几个时刻产生突变干扰，但不会影响到悬浮系统的动态特性。而对于a43而言，此时含参非线性项的常系数最大，辨识需要的时间最长，可表征为非线性项对该参数的影响最为明显，但是在70 s左右，逐步稳定，可以表征为通过辨识逐步缩小了非线性项在系统中的影响。根据上述辨识结果可以采用一定控制算法进行验证，当系统输入为9 mm的期望悬浮间隙、16 mm的初始状态悬浮间隙时，采用滑模控制得到如图9所示的悬浮间隙结果。

由于本文主要内容为基于神经网络构造逼近模型用于替代原本动力学模型，因此采用较为简单的控制即可验证模型效果。由图9还可看到，采用本文所辨识得到的系统参数同样可达到稳定的期望悬浮间隙(9 mm)。与此同时，在图3—图8中，通过对比计算结果可看出神经网络辨识结果收敛在线性化计算结果的很小范围内，由此证明了辨识结果可信。

4 结语

磁悬浮列车在柔性轨道上运行时，在受到轨道随机激励的情况下会出现明显振动现象。对动力学方程线性化处理的过程可明显降低分析难度，但同时也会丢失分析中某些重要的非线性特征，因此，采用系统辨识的思路避免了线性化处理，对含参非线性项进行辨识对于分析磁悬浮列车系统的复杂动力学行为具有重要意义。

1) 本文建立了基于柔性轨道的非线性动力学方程，并指出了其中的含参非线性项。

2) 针对Hopfield设计了辨识误差函数。在适当化简的基础上得到状态误差变化率的相关函数。此外，设计了相应的Hopfield神经网络辨识方案，得到了最终辨识结果具备的输出表达式。

3) 通过数值仿真的方式给出了辨识结果，证明了在假定输入信号为正弦函数时本文所设计辨识方案的辨识性能。可以判断当含参非线性项中常系数较大时，辨识过程更长，非线性项作用更为明显。a53需要65 s才能达到需要的辨识结果，而a43需要150 s才能达到要求。相反，a45在开始辨识时即能保证较为稳定的输出结果，在4.4 s达到的5×10-3的突变信号可通过滤波进行有效解决。

4) 所辨识模型相对非线性模型更为简单，并且最大程度地保留非线性特征，便于基于模型的动力学响应和控制算法的研究分析。但通过仿真发现辨识时间较长，可以在系统离线时进行辨识，在系统上线之后采用相应的辨识结果。

此外，文中基于柔性轨道建立的车-轨耦合系统运动方程以及辨识方案对于分析磁浮列车车-轨之间的控制性能具有指导意义。在实际应用中，非线性项不可避免，因此研究它们可能带来的非线性辨识问题对于修正动力学模型具有现实意义。