透射槽波相邻道质心频率的层析成像方法
2022-12-12吴荣新胡泽安杨巧楠
田 瀚,吴荣新,2,胡泽安,2,杨巧楠
(1.安徽理工大学 地球与环境学院,安徽 淮南 232001;2.深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南 232001)
近年来,煤炭工业无人化智能化开采成绩显著,然而我国煤炭开采条件复杂,安全生产仍面临多重挑战[1]。查明和重构煤炭开采透明化地质条件,确保采掘条件的可视、可预和可控,是精准开采和绿色利用的基础保障[2-3]。煤层开采过程中存在很多影响安全生产的小型地质构造(小断层和陷落柱等),常用的地面探测方法的精度无法满足其要求[4]。现阶段,矿井地球物理方法是小构造探测的常用手段[5],槽波勘探是其主要方法之一[6-10]。目前,槽波勘探主要是利用煤层工作面地质异常体对透射槽波能量衰减的影响,圈定其空间位置和形态[11-14]。
槽波信号采集过程中由于检波器耦合等因素,一般都存在较严重的噪声干扰,实测信号的保幅性较低。当工作面存在较大地质异常时会使槽波能量剧烈衰减,造成槽波信号的能量差异过大,成像结果中某些异常过于凸显而忽略了小异常。上述问题会降低直接利用槽波能量进行成像的适用性,需开发一种稳定性更高、适用性更强的数据处理方法。利用槽波频率域特征成像是一种比较好的槽波数据处理思路。质心频率偏移法最先由Quan Youli 等[15]提出,其主要原理是利用地震信号频谱高低频能量的统计学特征,故而受噪声和检波器耦合因素的干扰较小,具有更好的稳定性。通过现场实测数据和数值模拟计算,发现槽波信号同样具有质心频率偏移的现象[16]。通过槽波的频移处理,即可反演得到煤层工作面内地质构造的分布情况。
由于在透射槽波勘探中一般不采集震源信号,震源的质心频率,无法准确估算,一般给予质心频率一个经验值。由于炸药震源对激发条件敏感,实际探测中的质心频率很难一致,因此,该方法面临着质心频率估算困难且无法兼顾震源的差异性,求取的煤槽频移特征只能是一个相对值。笔者基于槽波的实测信号质心频率特征,提出通过相邻道质心频率来估算槽波质心频率的相对变化量,以期实现槽波精准成像,为煤炭透明化开采提供基础数据。
1 透射槽波实测质心频率成像方法原理
1.1 槽波质心频率移动现象
设距离震源X的任意点处信号能量为A,黏滞介质中槽波振幅衰减的简单关系可以用下式表示:
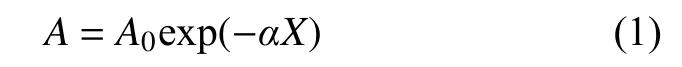
式中:A0为震源处的信号振幅;X为传播距离;α为振幅衰减系数。
α可表示为:

式中:Q为煤槽的品质因子;v为槽波的相速度;f为槽波的频率。
当f<1 000 Hz 时,透射槽波的α与f呈线性关系[17],则有:

式中:λ为槽波衰减系数的频率变化率。
由式(3)可知,透射槽波不同频率段其衰减系数存在差异。质心频率的变化特征符合地震信号振幅-频率谱的统计学规律。由于煤槽对槽波信号低频段的约束及高频段的衰减共同作用,造成槽波的能量主要集中在Airy 相附近较窄的频率范围内。当槽波在煤层中传播时,由于煤槽对不同频率槽波能量吸收强弱不同,基于槽波频谱的统计期望值必然向低频段移动,这为运用槽波信号质心频率进行成像提供了物理依据。
槽波质心频率受到低频段非线性衰减和高频段线性衰减的共同影响,衰减规律较为复杂。槽波质心频率与传播距离的关系,公开资料中未有定量化的理论公式。因此,为了研究槽波信号频移量与传播距离的定量关系,本文基于高阶交错网格有限差分法[18-19],数值模拟并分析槽波质心频率衰减特征。图1a 为二维数值模拟模型,模型均沿着中间煤层上下对称,煤厚10 m,模型具体物理参数见表1。震源点和检波点在一条测线上,道间距10 m,偏移距10 m,震源为120 Hz 主频的雷克子波点状源。模拟得到此模型的地震波信号,如图1b 所示;去除图1b 地震信号中的直达波,并分别求取接收点槽波信号的质心频率fR,求取结果如图1c 所示;接收点槽波信号的质心频率fR随着传播距离的增加而减小,整体呈现明显的线性衰减特征。

表1 数值模型1 物理参数Table 1 Physical parameters of numerical model 1
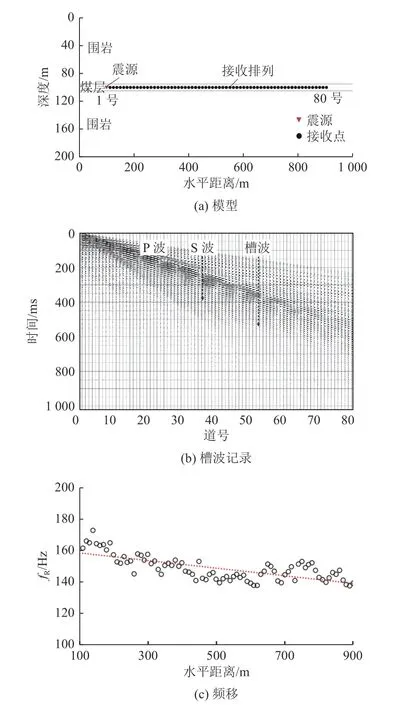
图1 槽波频移数值模拟Fig.1 Numerical simulation of in-Seam wave frequency shift
上述实验结果表明,通过实测透射槽波的质心频率变化并进行线性层析成像,得到槽波质心频率频移量在煤层工作面内的分布,运用槽波信号质心频率的变化特征进行工作面内成像是槽波勘探一个新的思路。
1.2 槽波频移成像方法原理及存在的问题
透射槽波质心频率fS的衰减与传播距离呈线性关系:
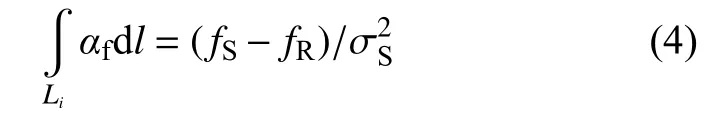
式中:Li为每道槽波传播路径总长度;l为槽波的传播路径长度;αf为槽波质心频率的衰减系数;为槽波的震源质心频率方差。其中,fR,fS,的表达式分别为:
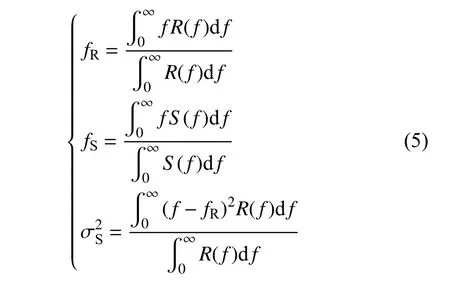
式中:S(f)为 槽波震源的振幅谱;R(f)为槽波实测信号的振幅谱。
假设fS、为已知量,则频移量是频率衰减系数沿槽波传播方向上的线性积分。在此条件下,槽波质心频率的频移量 (fS-fR)与煤槽的质心频率衰减系数近似呈线性关系。对每一道槽波信号均进行上述处理,并给定震源质心频率fS一个经验值,即可得到每一道槽波信号的频移量 Δf。此时,透射槽波的频移量从数学角度可以认为是αf沿其传播方向上的线积分。实际反演计算时需要进行离散化,则式(4)[20]可以表达为:
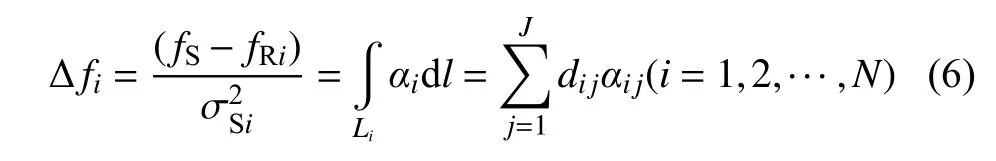
式中:Δfi为第i道槽波的总频移量;fRi为第i道槽波的质心频率;为第i道槽波的震源质心频率方差;αi为第i道槽波的频率衰减系数;αij为对应网格内的槽波频率衰减系数;dij为第i条射线上第j个网格中射线的长度;i是槽波接收道号,i=1,2,···,N;j为计算网格数,j=1,2,···,J;N为射线总数;J为网格总数。
由于在透射槽波勘探中一般不采集震源信号,槽波源的频率期望fS无 法准确估算,一般给予fS一个经验值。由于炸药震源对激发条件敏感,实际探测中所有震源的fS很难一致,因此,求取的煤槽值αf只能是一个相对值。然而在实际情况中,钻孔孔径大小、炸药深度以及钻孔碎屑物等因素,都会影响炸药震源的能量释放效果,导致fS的非一致性。若给定一个经验值,可能会导致成像产生较大误差。基于此,本文在前人的基础上进行了算法上的改进。
2 透射槽波实测质心频率的成像改进算法验证
2.1 算法改进
根据式(4),假定K=为定值,则式(4)可简化为:

根据式(7),则每个共炮点道集中第i道的相邻道质心频率计算为:

在透射槽波勘探观测系统中,相邻道传播路径相近,假定这2 条传播路径中的槽波质心频率衰减系数不变,则Kαi(Li+1-Li)=(fS-fi+1)-(fS-fi)=fi-fi+1,
可得:
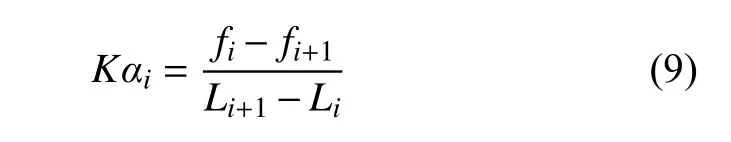
求取每炮所有实测槽波数据的质心频率fi和传播距离Li,并将基于式(9)计算得到的频率衰减系数,KαiLi定义为第i条传播路径上的质心频率衰减参数,即:
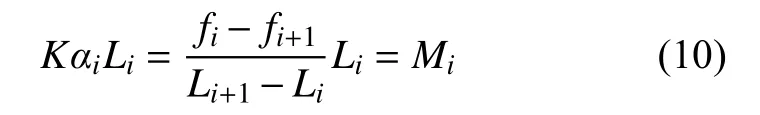
式中:Mi为每个共炮点道集中第i道槽波质心频率衰减参数,Hz,即相邻道槽波质心频率变化量。
实际反演计算时需要进行离散化,则式(10)可以表达为:
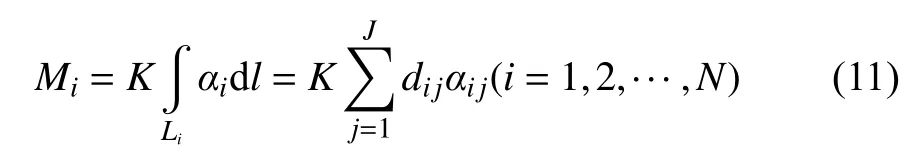
衰减参数Mi与传播路径呈线性关系,该参数由共炮点道集的相邻道槽波数据计算得到,避免了震源质心频率fS人为选择不当和非一致性对成像结果造成的影响。
2.2 方法验证
为了验证槽波质心频率计算改进算法的有效性,采用有限差分法进行了数值模拟实验,如图2a 所示。模型均沿着中间煤层上下对称,其具体物理参数见表2。震源点和检波点在一条测线上,道间距10 m,偏移距10 m。网格剖分大小为1 m×1 m,时间采样间隔为1 ms,采样时长1 024 ms,震源为120 Hz 主频的雷克子波点状源。模拟计算得到此模型的地震波信号,如图2b 所示。
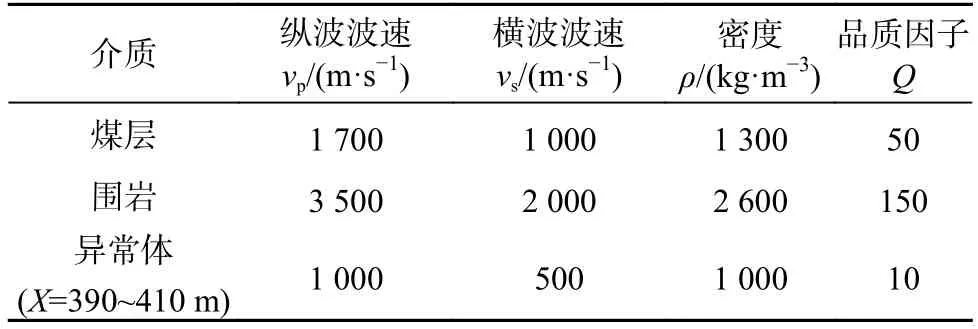
表2 数值模型2 物理参数Table 2 Physical parameters of numerical model 2
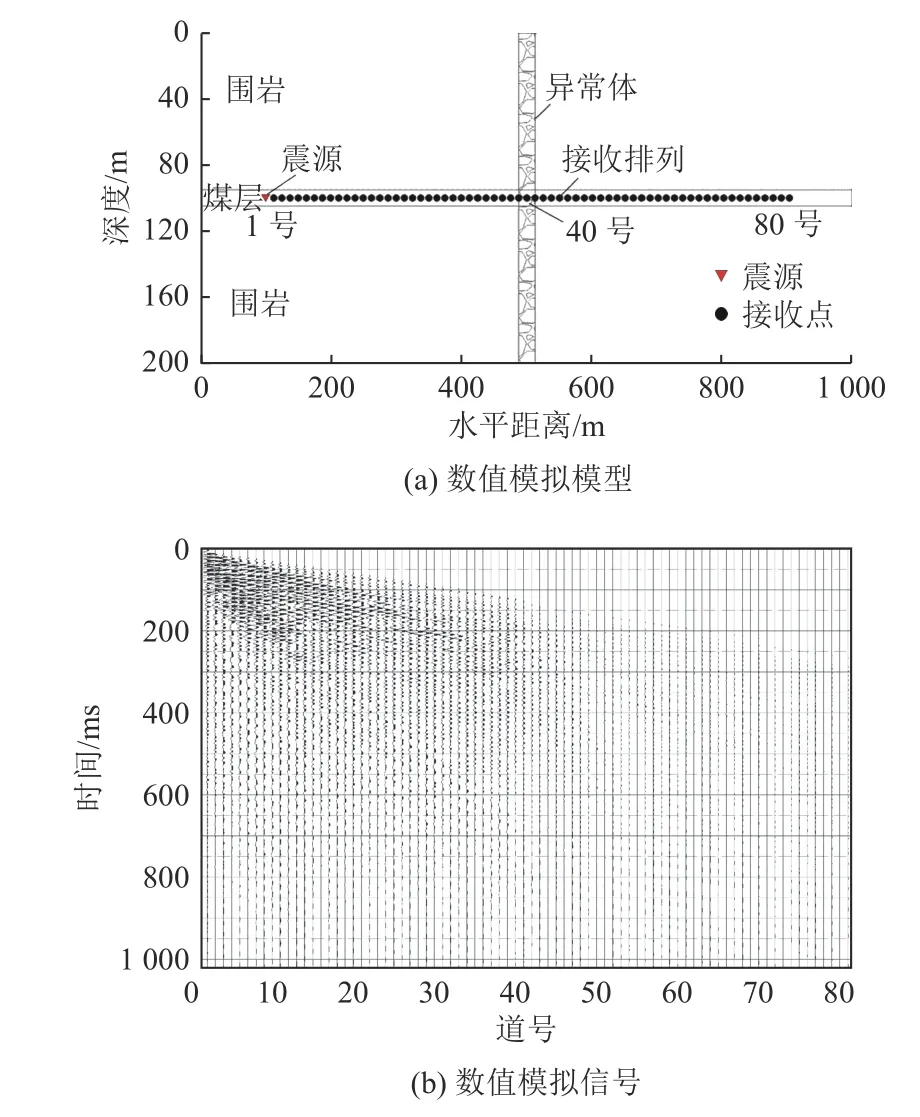
图2 二维数值模型及其信号(z 分量)Fig.2 Two-dimension numerical model and its signal (z component)
图2b 中槽波信号能量从39 道开始明显减弱。去除图2b 地震信号中的直达波,并分别求取接收点槽波信号的质心频率fR,结果如图3 所示。图3a 的结果整体呈现负线性衰减,在传播距离为400 m 处显示出明显的频率衰减异常。图3b 中频率变化幅度与图3a 基本一致,并且Mi值与传播距离呈现明显的线性正相关关系,变化率产生反转;在传播距离为400 m 处同样显示出频率变化异常。这些现象表明,相邻道槽波质心频率相对变化量Mi与地质异常的关系很敏感,可以作为槽波成像的有效参数。

图3 槽波模拟信号的质心频率fR 及衰减参数MiFig.3 Centroid frequency of in-Seam wave stimulation signals and Mi
3 实测数据成像算法试验
为检验上述槽波质心频率衰减特征和相邻道质心频率成像方法的效果,选择槽波发育的煤矿工作面进行现场试验。
3.1 试验概述
实测地点位于山东某煤矿1311 工作面,该工作面长度为330 m,宽度为186 m,倾角为20°~26°。煤层为3 号煤,煤层厚度6.9 m,H为断层断距。煤层顶底板均为厚细砂岩,结构简单(图4),是适宜的试验场地。沿工作面巷道布置震源和检波器,检波器点与炮点之间的距离设为10 m。由于采煤设备安全防护和巷道岩石的影响,实际布置了25 个检波点和33 个有效炮点。采用一炮多收的数据采集方法,共采集了32 个炮点道集。

图4 1311 工作面煤层开采地质简图及透射槽波试验观测系统Fig.4 Geological sketch of coal seam mining at 1311 working face,and test observation system of transmission in-seam wave
3.2 试验数据分析与成像方法的比较
选取1 组共炮点数据进行初步分析,第4 炮的实测数据及处理结果如图5 所示。图5a 为典型的煤层透射地震信号。该信号整体信噪比高,且透射槽波发育良好,满足了透射槽波成像方法的数据质量要求。图5b 为第4 炮实测槽波数据的质心频率,其衰减与传播距离呈现明显的线性关系。图5c 为第4 炮实测数据基于相邻道质心频率估算槽波质心频率相对变化量Mi。其整体形态与fR曲线类似,且与传播距离呈线性正相关,可以直接用于线性层析成像。给定不同fS值对实测槽波数据进行估算处理,对不同fS值估算的衰减数据进行成像处理,得到透射槽波质心频率衰减成像结果(图6)。
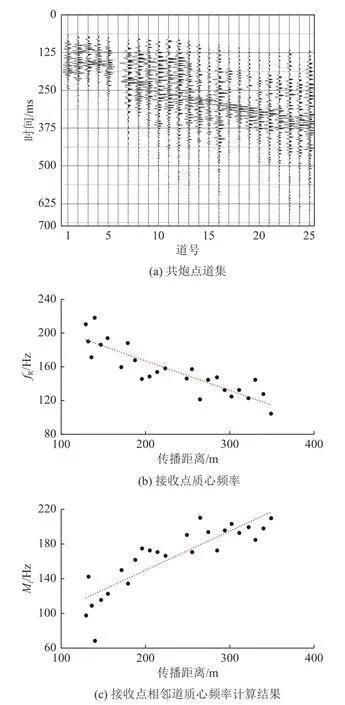
图5 第4 共炮点道集的信号fR 和MiFig.5 Signal fR from 4th shot of common shot point gather,and Mi
图6a-图6c 是槽波的不同质心频率衰减成像结果,图6d 为常规槽波能量衰减系数成像结果。其中,CF3和CF5断层实际回采中未揭露,常规槽波能量衰减系数成像结果在此处存在误差;经过信号比对分析,CF5断层附近12-15 号震源能量偏低、一致性较差;第28 号震源的19 道信号与相邻道信号相比能量偏低,可能是因为检波器耦合不佳导致成像结果在CF3断层附近出现误差。CF1断层为实际新揭露的走向连续断层,常规槽波能量衰减系数成像结果中有较强反映,但形态刻画精度不够。通过与槽波能量衰减系数成像对比,透射槽波质心频率衰减系数成像结果能够在一定程度上反映实际的煤层地质构造情况,基本可以达到能量衰减系数成像的分辨率。当选定fS=250 Hz 时,其成像结果相较于fS=300 Hz 和350 Hz,能更好地刻画工作面中的地质异常构造;CF3和CF5未见异常,CF1断层形态显示准确。由于炸药震源对激发条件敏感,实际探测中fS很难一致,因此,该方法面临着fS估算困难且无法兼顾震源的差异性,该方法反演得到的槽波频移特征只能是一个相对值。
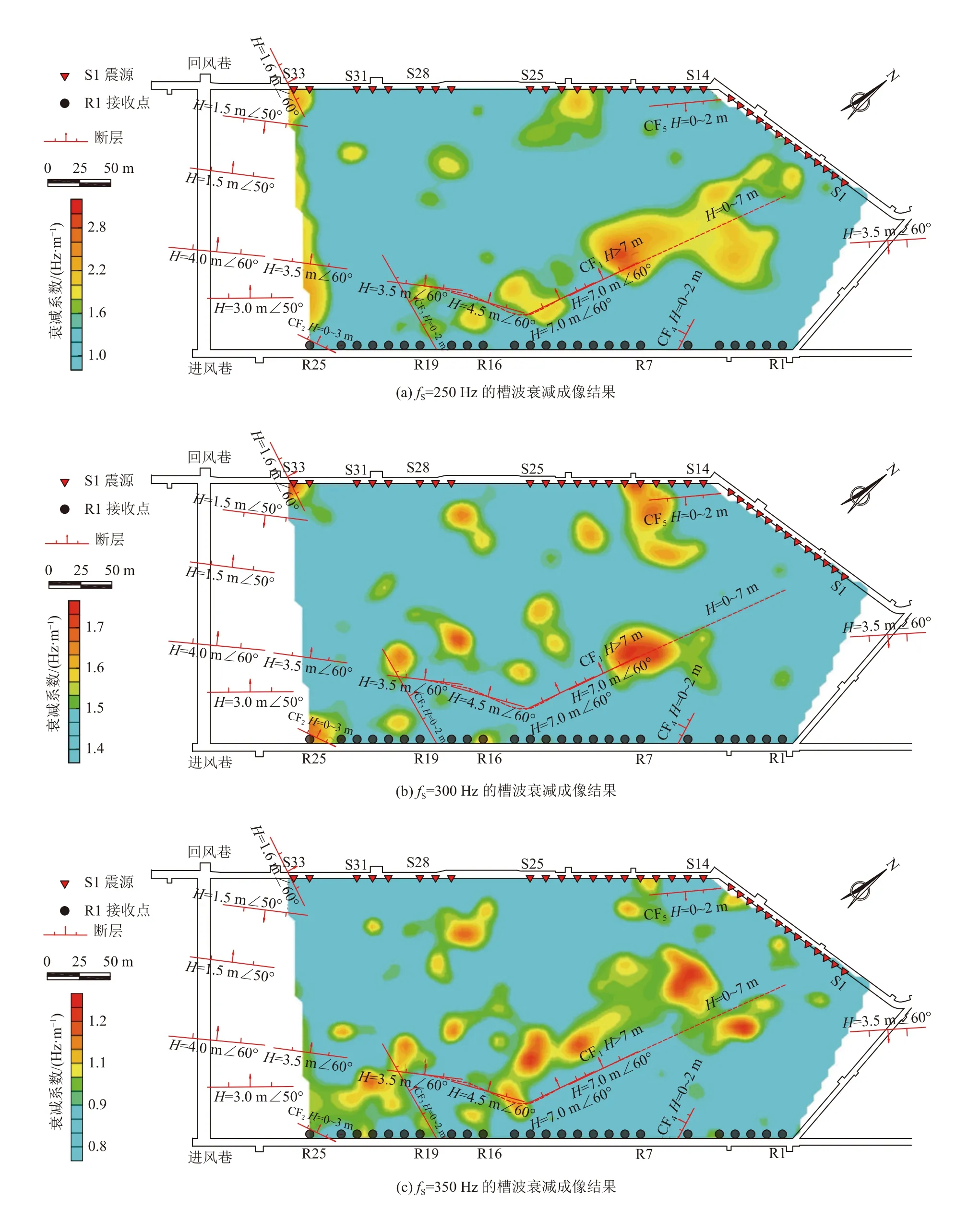
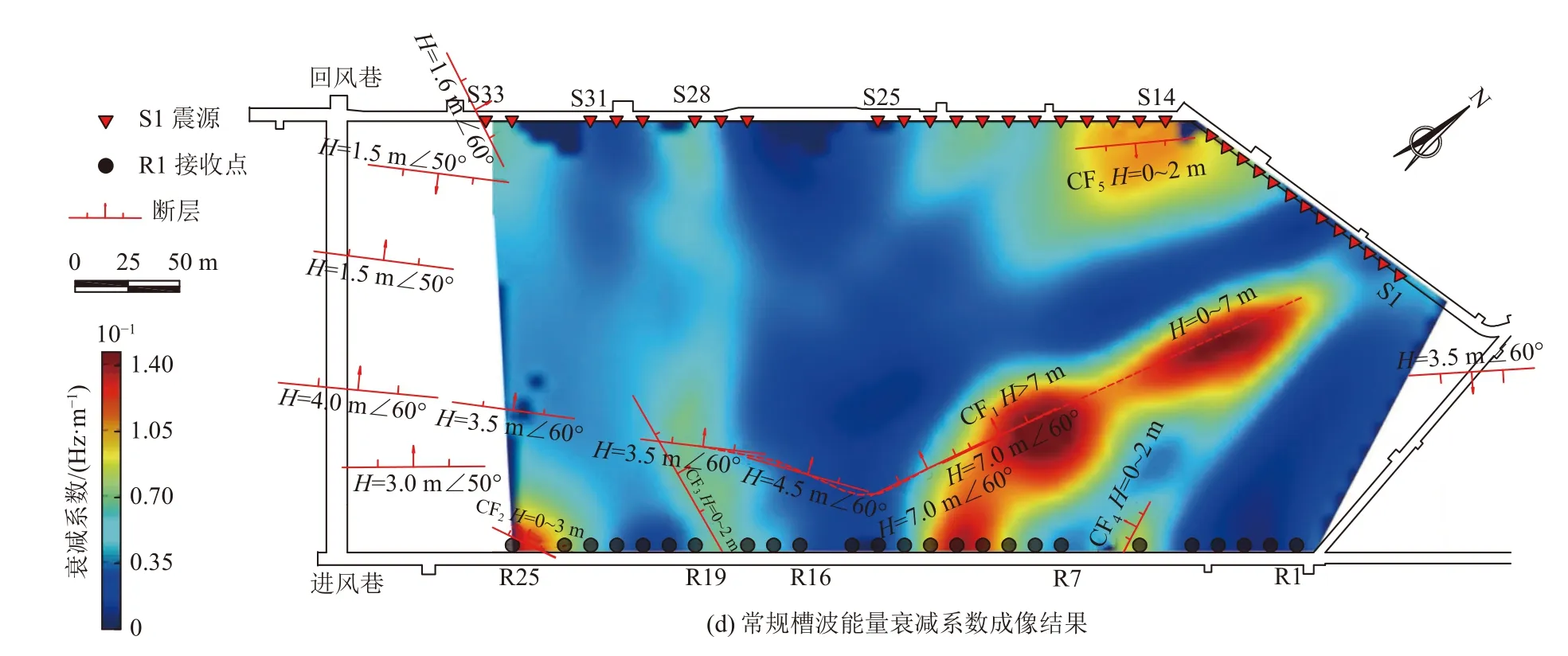
图6 槽波质心频率衰减和能量衰减成像结果对比Fig.6 Imaging result comparison of in-Seam wave centroid frequency attenuation and energy attenuation
通过相邻道质心频率来估算槽波质心频率的相对变化量Mi,进而实现了该工作面实测槽波数据的质心频率成像,如图7 所示。由图中可知,相邻道质心频率估算衰减特征与地质异常的关系敏感。其中CF3和CF5为三维地震预测断层,实际回采中未揭露,基于实测槽波信号的相邻道质心频率层析成像结果与实际相符;CF1断层为实际新揭露的走向连续断层,槽波相邻道质心频率成像准确预测。对比成像结果和验证结果,该成像方法可以精准地反映煤层工作面中的地质构造分布,取得了较好的应用效果。与槽波的不同质心频率衰减成像结果相比,该方法成像结果避免了震源差异性和fS人为选择不当对成像结果造成的影响。
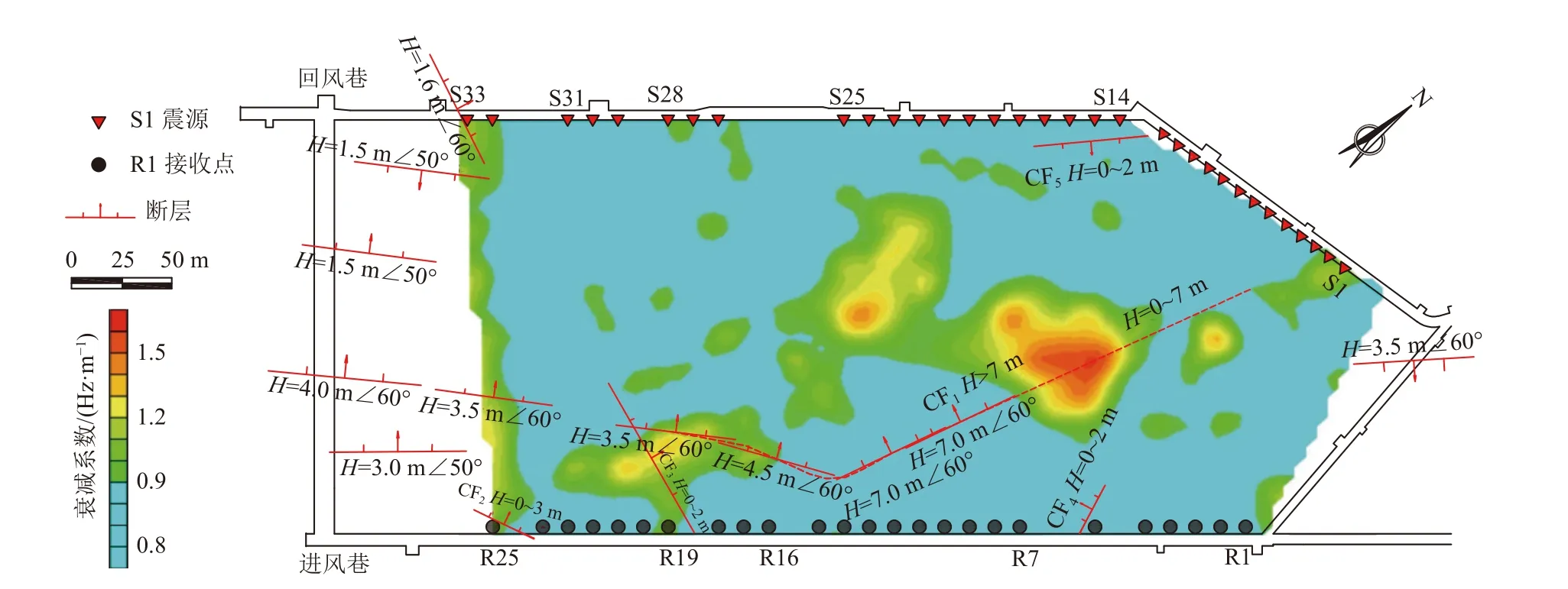
图7 基于实测槽波信号的相邻道质心频率层析成像结果Fig.7 Frequency tomography results of adjacent channel centroid based on measured in-seam wave signals
4 结 论
a.基于理论分析、数值模拟和实测数据分析,证明槽波信号存在频移现象,槽波的频移量和传播距离呈现明显的线性衰减规律。槽波的质心频率衰减特征与地质异常关系敏感,可以作为槽波勘探层析成像的有效参数。
b.提出的基于相邻道槽波质心频率层析成像方法,该方法可准确估算槽波质心频率的衰减变化,且克服了震源差异性和震源质心频率人为选择不当对成像结果造成的影响,为槽波勘探的数据处理提供一种新的思路。
