数控切削加工过程动力学建模、仿真分析回顾与展望*

李忠群 ，张伟峰 ，刘 阳 ，刘 鸿 ，杨尚臻

（1.湖南工业大学，株洲 412007；2.北京航空航天大学江西研究院，南昌 330096）

众所周知，机械制造业在整个国民经济中占据重要地位，而金属切削加工又是其最基本和最可靠的加工手段。数控切削加工过程中，刀具与工件按事先指定的程序路径相对运动，从工件上切下多余的材料，其实质是一种由挤压产生的弹塑性变形过程，该过程伴随着切削力和切削热的产生。在切削力的作用下，工件产生加工变形，引发刀具与工件的振动，触发颤振；在切削热的作用下，工件表面材料发生相变，产生加工硬化和残余应力。切削力和切削热是影响切削加工质量和效率的两个最为重要因素。因此，基于切削过程建模与仿真分析进行工艺参数优化，对于实现高速、高效数控加工至关重要。

基于切削过程的仿真技术是虚拟制造与数字化制造的底层关键技术，其研究内容涵盖几何仿真与物理仿真两大方面[1]。几何仿真最早出现在CAD领域，它侧重于分析工件的几何约束与刀具的轨迹规划，不考虑切削力、振动和切削热等物理因素，主要用于验证NC程序和刀具轨迹的正确性。物理仿真亦即动力学仿真，在明确刀具与工件几何信息及相关约束的基础上，基于动力学和金属切削理论，在物理层次上建立仿真模型，实现对切削过程中的切削力、切削温度、表面形貌、加工变形、刀具磨损和加工稳定性等预测[2]，其实质是利用物理规律去模拟切削加工过程。目前，物理仿真的实现方法主要有数学建模分析与有限元分析两大类。数控切削加工动力学仿真技术路线如图1所示。

图1 切削过程动力学仿真技术路线图Fig.1 Road map of dynamic simulation technology of cutting process

1 切削过程动力学建模分析与切削力预测

通常，基于切削过程的动力学建模分析方法可归纳为以下几类。

（1）试验辨识方法。把切削过程当作 “黑箱”处理，通过一系列切削试验，对切削力、表面形貌、刀具磨损等物理量进行测量，并进行模型辨识，建立起切削过程参数与刀具几何角度、切削用量等切削条件之间的经验公式。试验辨识方法实用性强，但也存在显著缺陷：一方面模型辨识需要大量的切削试验作支撑；另一方面经验公式的适用条件受限。

（2）切削机理分析方法，又称解析法。以金属切削理论和多体动力学为基础，从理论角度出发，通过适当的假设与简化，建立起切削过程各物理量之间的动力学关系，以实现对切削力和切削稳定性等的预测，是深入研究切削过程本质的基础。最典型的机理分析方法当属Merchant[3]的正交切削模型和Oxley[4]的斜角切削模型。

（3）混合建模方法。该方法结合了切削机理分析与试验辨识方法各自的优点，基于切削机理研究，结合少量切削试验来辨识部分模型参数。将切削力看成是切削面积的函数，其中的系数与刀具几何结构与涂层材料、工件的材料特性以及冷却润滑条件密切相关，并可通过切削力系数辨识试验获得[5]。

1.1 静动态切削力建模与仿真

静态切削力建模是指假定工艺系统为刚性的前提下，根据刀具与工件的啮合情况来确定切削力及工件的表面形貌。当工艺系统刚性较好时，静态切削力模型可以获得较好的预测精度。瞬时刚性力模型把切削力看成是切削面积的函数[6]。由于不同轴向高度处的切削刃的径向滞后角不同，导致其参与切削的先后次序不同，为消除这种影响，需要对切削刃进行离散化，亦即沿轴向将切削刃分割成一系列微元，然后计算每个微元上的切削力，通过力的合成与分解得到作用在整个刀具上的瞬时静态切削力。

若切削系统为弱刚性 （刀具和/或工件弱刚性），在切削力的作用下，刀具和工件会发生变形，从而导致理论切屑厚度与实际切屑厚度不一致。因此，要实现切削力的准确预测，切削力模型中必须考虑由切削力所引起的切屑厚度的动态变化。下面以二自由度铣削系统为例，说明其动态切削力建模过程。考虑再生效应的动态切削力模型可由如下二阶时滞微分方程表示[7]：

式中，m、ζ、ωn分别为模态质量、阻尼比和固有频率；ap为轴向切深；N为刀齿数；Kt、Kn分别为切向和径向切削力系数；g（φj（t））表示当前时刻切削刃j是否参与切削。通过求解时滞微分方程，可得到诸如切削力、刀具振动等切削过程参数；也可以进一步通过时频转换，在频域内进行切削过程稳定性分析。

1.2 切削力建模分析拓展研究

基于切削过程静动态切削力模型，众多学者对切削力建模分析进行拓展研究，为满足具体的应用对象，许多拓展的切削力模型被相继提出，现归纳如下。

（1）建立通用切削力模型，使模型的适用性更强。Engin等[8]构建了立铣刀通用几何模型及切削力模型，涵盖的刀具类型包括圆柱螺旋铣刀、鼻头铣刀、球头铣刀和圆锥球头铣刀等。Li等[9]建立了镶齿铣刀通用几何模型和切削力模型，模型中不同数量、不同几何形状的刀片可以按指定的空间位置阵列。Zhang等[10]提出了一种通用螺旋铣刀外圆铣削切削力预测模型，该模型对铣刀进行了参数化定义，并考虑了刀具跳动 （偏置和倾斜）的影响。

（2）建立更为精确的切削力模型，以满足特定的应用对象。Azvar等[11]借助Tri-dexel引擎实现了刀具–工件啮合计算及工件几何更新，使用利勃海尔LC500的CNC信号进行运动学建模，进而实现滚齿过程切削力的预测。针对面铣螺旋锥齿轮时展成运动的复杂性，Zheng等[12]将未变形切屑归纳为6种情况，并用二次多项式插值来描述，进而实现其切削力的预测。该方法预测精度高、计算速度快。针对Inconel 718的激光辅助铣削，Pan等[13]通过构建三维模型来计算激光预热引起的温度场，并在此基础上引入OXLEY接触力学来建立铣削力解析模型，仿真结果显示，激光辅助铣削与传统铣削相比可显著降低铣削力。

（3）建立面向走刀轨迹的切削力模型，实现三维切削力仿真。针对球刀三轴铣削复杂曲面，Wei等[14]提出了一种采用Z级轮廓刀轨预测切削力的方法，该方法将整个走刀轨迹离散化，使用高效的Z–map方法来求取刀具与工件的啮合。Li等[15]通过圆角几何建模，实现了圆角铣削动态切削力预测。基于铣削过程的三维摆线轨迹，Zheng等[16]建立了铣削表面未变形切屑厚度的模型，分析了切削刃处于不同离散位置时切屑厚度变化规律，建立了面向曲面铣削的切削力模型，并得到了切削试验的验证。

1.3 表面形貌预测研究

表面形貌 （Surface topography）是指切削过程中，因刀具安装误差、切削刃形状误差与磨损、切削振动、积屑瘤等因素影响，在零件加工表面残存的各种不同形状大小的微观凸峰和凹谷[17]。表面形貌直接影响零件的工作精度和使用寿命。表面形貌预测主要有以下几类方法：

（1）沿走刀路径利用刀刃所形成的包络面约束，与工件进行求交，从而获得已加工表面的形貌，该方法计算效率高。Wang等[18]提出了一种表面形貌预测模型，该模型以椭圆轨迹作为周铣三维形貌的切削刃轨迹，进而实现其表面形貌预测。Chiou等[19]以预测得到的最大残留高度为指标，提出了基于最大势能场的刀具轨迹规划方法。Gray等[20]评估了五轴铣削中的刀具位姿对已加工表面轮廓的影响。

（2）基于Z–map的方法。首先将工件进行网格化处理，并计算各网格节点的z坐标值z（x，y）。基于 Z–map模型，Zhu等[21]实现了球头铣刀五轴加工自由曲面的表面轮廓预测。 Omar等[22]以立铣加工为对象，采用Z–map模型研究了刀具回转误差对工件表面形貌的影响。Liu等[23]研究了刀具偏心及切削刃磨损等对五轴铣削加工表面形貌的影响。对基于Z–map的表面形貌预测模型来说，工件网格越精细，预测精度越高，但计算效率会显著下降。

（3）考虑加工系统动力学特性的表面形貌预测方法。李忠群等[24]基于Z–map模型构建了考虑再生作用的铣削动力学模型，并通过数值求解方法在 Matlab平台上实现了周铣工件三维表面形貌预测，如图2所示。基于改进的Z–map模型，通过构建螺旋铣孔运动学与动力学模型，Li等[25]实现了螺旋铣孔表面形貌预测，并分析工艺参数等对待加工孔表面轮廓质量的影响。梁鑫光等[26]提出了基于动力学响应的球刀五轴铣削表面形貌预测模型，可对颤振及稳定两种工况下的表面形貌与纹理特征等进行准确预测。

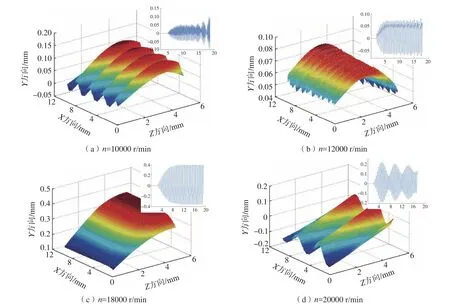
图2 周铣主轴转速对表面形貌及刀具振动的影响[24]Fig.2 Eあect of spindle speed on surface topography and tool vibration in peripheral milling[24]

1.4 切削力系数辨识

准确辨识切削力系数是切削力预测和切削过程稳定性分析的关键，试验辨识切削力系数主要有平均力和瞬时力两种方法。前者在保持径向和轴向切深不变条件下，每改变一次进给速度进行一组切削试验，通过测量每个刀齿周期的平均切削力，并用最小二乘法将每齿平均力和每齿进给量拟合成线性函数。后者则基于最小目标函数，通过一次切削试验对模拟力和实测力进行拟合，反推得到切削力系数。

平均力法是由Yücesan等[27]提出的，因其模型简单且计算量小而被广泛应用。但该方法得到的切削力系数辨识精度较低，且需要大量的切削试验支撑。瞬时力法是由Cheng等[28]提出的，该方法只需要做一次切削试验，且辨识精度较高。Wang等[29]对线性瞬时切削力法和非线性平均力法进行了对比，发现线性瞬时切削力法的辨识精度更高。

材料的切削力系数会随着切削参数不同而改变。Campatelli等[30]研究了不同主轴转速对铣削力系数的影响，得出低主轴转速时主轴转速对切削力系数影响较大。Rubeo等[31]采用瞬时切削力法结合非线性优化对不同切削参数对切削力系数的影响进行了研究，发现切削参数和切削力系数呈非线性关系。Yu等[32]研究发现与轴向切深相比，主轴转速对切削力系数的影响较小。

此外，不规则刀具和切削方式均会影响切削力系数值。小径向切深和每齿进给量特别小时，变齿距和变螺旋角铣刀也会影响切削力系数值[33]。不同的切削方式，如插铣[34]、平面端铣[35]和球铣[36]等均会影响切削力系数的大小。

1.5 加工系统动态特性

获取加工系统动态特性参数（模态参数或频响函数）是进行切削过程仿真的前提条件。机床、刀具和工件的几何结构、刀具与工件在机床上的装夹状况、工件材料的切除过程以及主轴转速的变化等，都会直接影响加工系统的动态特性参数。如图3所示[37–38]，可通过试验或仿真方法获得加工系统的动态特性参数。

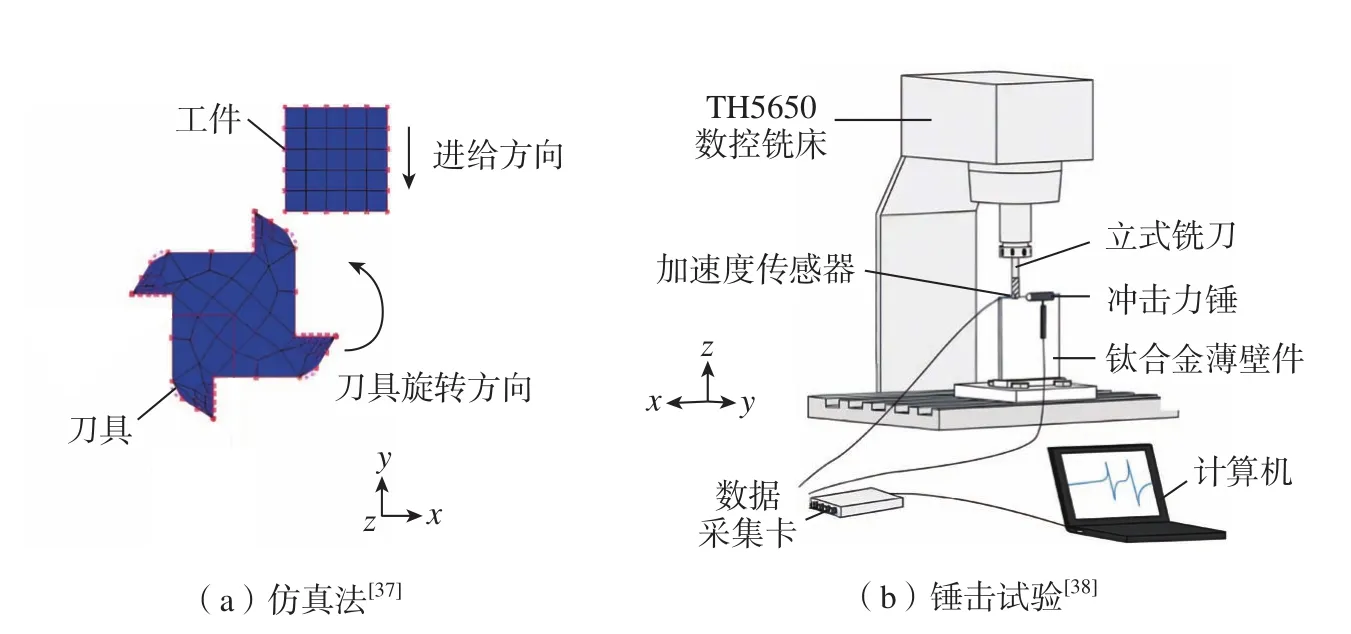
图3 仿真法和锤击试验获取动力学特性参数Fig.3 Schematic diagram of dynamic characteristic parameters obtained by simulation method and hammer test

锤击试验是获取加工系统频响函数 （Frequency response function，FRF）的最简便方法，但该方法也存在不足：一方面，主轴上刀具的装夹状况、薄壁工件材料的不断切除等均会显著改变加工系统的动力学特性，不可避免造成测试工作量大；另一方面，由于加工系统的动态特性在主轴高速旋转与静止状态时存在显著差异，静止状态得到的测试结果难以准确反映其实际工作状态。目前，可供选择的技术途径有以下两条。

（1）子结构响应耦合法（Receptance coupling substructure analysis，RCSA）。利用该方法，结合锤击试验和解析法，可获得刀具在主轴上不同安装状态下的动态特性[35，39]，可节约大量试验时间。

（2）有限元仿真法。通过对加工系统进行结构建模，采用有限元方法直接获得系统的动态特性，该方法无须进行大量试验且预测精度较高，故被广泛采用。Song等[40]针对刀具位置变化和材料的去除过程，利用有限元法获得薄壁件的动态特性。Budak等[41]采用有限元法和结构动态修正法相结合，系统分析了工件固有频率随材料去除和加工位置的变化规律。

2 切削稳定性分析

颤振是指发生在切削过程中的一种自激振动现象，是影响零件表面质量、加工效率、刀具磨损和机床主轴寿命的关键因素。根据产生的机理不同，颤振可细分再生型颤振、振型耦合型颤振以及摩擦型颤振，其中以再生型颤振为主[42]。切削加工过程中，在周期性切削力的作用下，导致留在弱刚性切削系统的切屑内外表面振纹的相位差不同，进而引发再生颤振。

有关切削颤振的研究，最早可追溯到20世纪60年代，Tobias提出了切削颤振的解析模型，并创新性地引入了稳定性叶瓣图 （Stability lobe diagram，SLD）概念，从而奠定了切削稳定性的理论基础。基于切削过程动力学建模，稳定性分析旨在获取稳定性叶瓣图，并根据稳定性叶瓣图选择优化的切削参数，进而实现高效、无颤振切削。目前，切削稳定性分析方法主要有频域法、时域法等。

地方特色课程——《走进某地》。体现特色和接近性。可以设计成社会、政治、经济等系列讲座形式。如西湖寻梦——《走进杭州》。

2.1 频域法

频域法又叫解析求解法，通过频域稳定性判据来确定临界切削深度，可分为零阶近似法 （Zero-order approximation，ZOA）和多频域法（Multi frequency，MF）两种。ZOA方法最早由Altintaş[43]提出，采用傅里叶级数展开表示动态铣削因子，忽略谐波的影响且仅保留直流分量。该方法计算速度快，但预测精度不高，尤其不适合小径向切深条件。2004 年，Merdol等[44]提出多频域法，该方法由于考虑了傅里叶级数的谐波，故预测精度得以提高，但计算量大幅度增加，导致仿真速度减慢。此外，由于模型中并未考虑实际加工中的非线性因素，导致获取的稳定性叶瓣图并不可靠。如图4所示[45]，稳定性频域分析法的求解步骤如下：

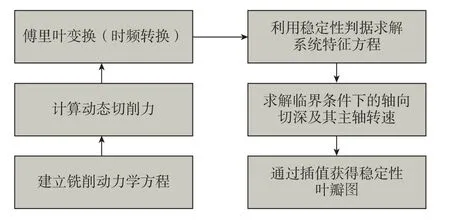
图4 频域稳定性分析基本步骤[45]Fig.4 Basic steps of chatter stability analysis in frequency-domain[45]

（1）建立考虑再生效应的时滞微分方程，并推导出动态切削力与切削参数之间的关系式；

（2）利用周期函数的傅里叶级数展开，对时变的有向切削力系数作近似处理，将时域稳定性问题转化为频域稳定性问题；

（3）利用Nyquist稳定性判据，确定临界切削条件；

（4）计算临界状态下的轴向切削深度及其对应的主轴转速；

（5）通过插值处理绘制出稳定性叶瓣图。

基于经典ZOA方法，学者们对切削稳定性分析方法进行了诸多拓展。

（1）面向各种几何结构与形状铣刀的改进ZOA模型。Engin等[8]构建了立铣刀通用几何模型，并实现了其切削力和铣削稳定性预测。Li等[9]在镶嵌铣刀几何建模的基础上，采用数值方法求取平均有向切削力系数，实现了镶嵌铣刀切削稳定性预测。变齿距铣刀的刀齿沿铣刀周向不规则分布，可扰乱相邻两振动周期间的相位，以达到抑制颤振的目的。Slavicek[46]、Altintas[47]等先后对变齿距铣刀抑制颤振的机理进行了研究，发现改变铣刀的齿间角和螺旋角可扩大铣削稳定域面积并对齿间角进行了优化。

（3）将经典的二维稳定性叶瓣图拓展到三维甚至多维。针对机床刀具系统和机床工件系统均为弱刚性的情形，Bravo等[50]根据刀具与工件的相对运动实现了薄壁零件铣削三维稳定性叶瓣图的预测。针对T型槽铣削，Li等[51]基于获取的经典稳定性叶瓣图，通过改变径向切深进行仿真获得了三维稳定性叶瓣图（图5），以供T型槽铣削切削参数选择用。

图5 T型槽铣削三维颤振稳定性叶瓣图[51]Fig.5 3D chatter stability lobe diagram of T-slotted milling[51]

2.2 时域法

时域法是指对时域数据采用稳定性判据，以确定当前切削条件下加工系统是否稳定，进而获得稳定性叶瓣图，该方法可细分为半解析法和数值仿真法两大类。

2.2.1 半解析法

半解析法包括半离散法 （Semi discretization method，SMD）和全离散法 （Full discretization method，FMD）。SMD最早由Insperger等[52]于2002年提出，其可以对任意转速下的稳定性极限进行预测，与ZOA方法相比（图6[52]）大幅提升了稳定性的预测精度，尤其适合小径向切深铣削稳定性预测。随后，为进一步提高该算法的精度，Insperger等[53]提出了高阶半离散算法。随着算法阶次的增加，计算效率大幅度下降。2010年，Ding等[54]提出了FDM，将时滞项和状态项进行离散处理，极大地提高了算法的收敛速率和计算精度。

图6 SMD与ZOA仿真结果对比[52]Fig.6 Comparison of simulation results between SMD and ZOA[52]

2015年，在SDM方法的基础上，Li等[55]提出了基于Runge-Kutta的全离散法，该方法对时滞微分方程的状态项、时滞项以及参数项进行4阶Runge-Kutta法迭代，大大简化了迭代公式的复杂性，仿真结果显示该方法具有较高的收敛速度和预测精度。2017年，Tang等[56]提出了一种基于状态项和时滞项高阶插值的铣削稳定性预测全离散化方法，研究了时滞项高阶插值对铣削稳定性预测精度的影响。2017年，Zhou等[57]提出了对时滞项进行拉格朗日插值的2阶、3阶、4阶全离散方法，发现利用拉格朗日插值的 4 阶全离散化法在划分40个时间间隔时预测精度最高。2018年，Dai等[58]提出了基于精密积分法的全离散方法，并将其与基于全离散的龙格–库塔法和全离散的欧拉法比较 （图7），发现精确积分法有较高的收敛率和预测精度。2019年，黄超等[59]采用3阶牛顿–埃尔米特插值全离散法预测铣削稳定性，发现该方法的计算精度和计算效率都好于1阶和2阶全离散法。

图7 基于精确积分的全离散法与其他类型全离散法对比[58]Fig.7 Comparison of precise integration based on FDM and other FDMs[58]

2.2.2 数值仿真法

数值仿真法是指直接对时滞切削动力学微分方程求解，获得包括切削力、刀具与工件振动在内的切削过程参数，对仿真数据施用某种或某几种时域稳定性判据，判定当前切削条件下切削系统是否稳定，进而获得稳定性叶瓣图的过程。图8所示为数值仿真稳定性分析方法一般流程：

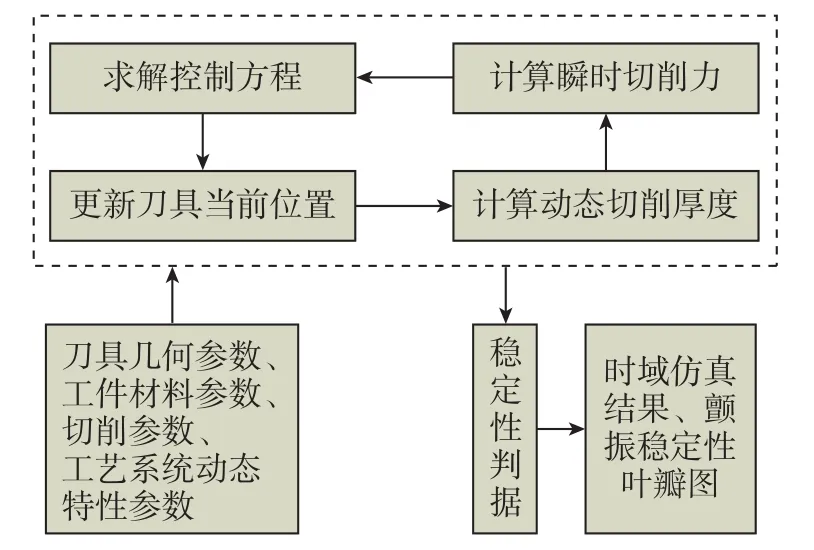
图8 基于数值仿真的稳定性分析方法一般流程Fig.8 General steps of stability analysis based on numerical simulation

（1）建立切削系统时滞动力学微分方程；

（2）对连续时间变量作离散化处理，采用数值方法直接求解微分方程；

（3）根据求解结果更新刀具位置并计算动态切削厚度；

（4）计算当前时刻的动态切削力；

（5）判断仿真是否结束，若未结束跳到步骤（2）；

（6）对仿真数据施用某种稳定性判据，判断当前切削条件下加工系统的稳定性；

（7）改变主轴转速和轴向切深，重复步骤 （2）~（7）。

鉴于数值求解方法是基于所建立的时滞切削动力学模型，模型中可以考虑诸如刀具几何参数、刀齿偏心、刀齿因振动脱离切削区、多维结构动力学、非线性切削力系数等对稳定性的影响，故预测精度较高[60]。另外，数值求解方法需要针对各种不同的切削条件求解微分方程，计算量大、耗费时间长。

在获取切削过程时域数据后，寻找有效的时域稳定性判据非常关键，目前常用的时域稳定性判别方法主要有时域法、频域法和时频域法3大类。

（1）时域分析又叫波形分析，它直接对仿真数据的原始序列进行分析。Ye等[61]对时域采样序列的均方根进行计算，然后将均方根序列的标准差和均值的比值作为变异系数，用来识别颤振。Schmitz[62]以刀尖位移数据的标准差作为颤振的判定标准。时域分析方法虽然简单直观，但由于其特征信息并不显著，故可能造成对切削状态的误判。

（2）频域分析又称为频谱分析。颤振发生后，切削能量将集中在系统固有频率附近而非切削频率及其谐波频率处，故根据频谱的能量分布可确定是否存在颤振。Frumusan等[63]通过对切削力信号进行FFT变换，将给定频域内切削力信号幅值最大值与平均值的比值作为稳定性判据。熊振华等[64]针对颤振在孕育阶段的特征信息较弱，提出了基于尺度因子的插值傅里叶频谱估计算法。由于傅里叶变换属整体变换，无法提供准确的时间定位信息，故经由其处理的加工过程信号准确性有限。

（3）时频域方法吸收了上述两种方法的优点，能够实时捕捉颤振发生的初期信号，故其分析精度较高。常用的时频域分析方法主要有小波变换、经验模态分解和变分模态分解等。

小波变换对信号的低频部分有很好的分解功能，对高频阶段则效果不明显。张钊[65]利用颤振发生过程中能量聚集原理，对信号进行小波包分解，计算子信号的能量熵和能量分布，从而识别颤振。熊振华等[64]针对颤振孕育阶段特征薄弱和算法复杂度低等难点，提出了加权小波包熵实时辨识方法。Zhang[66]对采集的信号进行小波包分解，发现颤振发生过程中，信号的分布呈现明显的规律，利用能量熵描述能量分布可识别铣削加工状态。

经验模态分解方法 （Empirical mode decomposition，EMD）基于信号的局部特征时间尺度，将一个复杂的信号函数分解为一组完整的、正交的分量，即固有模态函数。Fu等[67]首先将信号进行EMD分解，然后对选择的能量极限系数进行希尔伯特黄变换得到HHT时频谱，并计算其归一化能量比和变异系数来识别颤振。Liu等[68]将原始信号进行EMD分解后，运用频域特征挑选和原始信号波形相似的能量极限系数分量进行信号重构，计算第3层各节点的能量熵，对能量熵最大的频率带进行希尔伯特黄变换，计算其瞬时频率的均值和标准差作为颤振判断标准。

变分模态分解的原理是首先假设各个模态具有不同的频率，之后使用交替方向乘法算子迭代更新各模态及其频率，最后得到各模态及其对应的中心频率和带宽[69]。Li等[70]为了在颤振发生的早期阶段识别颤振，提出基于变分模态分解和功率谱熵差用于监测颤振。为了找到对颤振更敏感的指标，Liu等[71]用变分模态分解和能量熵实时监测颤振。

3 切削过程有限元仿真

求解切削加工相关问题的方法主要有两类：解析法和数值法，前者一般适合方程简单且边界条件比较规则的少数问题，而对于绝大多数问题，则需要研究其数值解。以有限元法为代表的数值求解方法因其通用性最好，而被广泛采用。目前，有限元仿真被广泛应用于切削加工领域，成为研究切削加工机理、预测切削力、切削加工变形、表面完整性及刀具寿命强有力的工具。目前，支持切削过程仿真的主流有限元软件主要包括 Abaqus、Deform、AdvantEdge、Ansys和Marc等。基于材料的本构模型，通过构建切削过程仿真模型，可以准确地对切削过程中的应力、应变、应变率、切削力和切削温度等物理量进行预测，进而为研究刀具磨损、加工表面完整性和工艺参数优化提供依据。

3.1 切削过程有限元仿真关键技术

3.1.1 材料本构模型

材料的本构关系揭示了材料在热加工变形条件下流动应力与应变、应变率和温度之间的关系。由于切削加工状态下的工件处在高温、高应变和高应变率状态，材料本构关系的精确与否直接影响有限元仿真结果的准确性，选择或建立符合材料自身属性的本构关系对切削仿真至关重要，材料的本构关系可表示为：

式中，σ为流动应力；ε为材料应变；为材料应变率；T为切削温度；ζ为材料变形。

常用的材料本构模型主要有Johnson–Cook模型 （简称J–C模型）[72]、修正的Johnson–Cook模型[73]、Zerilli–Armstrong模型 （简称Z–A模型）[74]、Power–Law模型[75]等。其中，J – C本构模型能较好地反映切削加工中的3种效应，故在切削加工仿真中被广泛采用，其表达式为

式中，A、B、n、C和m分别表示材料的初始屈服强度、硬化模量、应变硬化指数、应变率敏感系数和热软化系数；Tr和Tm分别表示参考温度和材料熔点温度。J–C本构方程的参数通常借助霍普金森压杆 （Split Hopkinson press bar，SHPB）试 验，对不同温度和不同应变率条件下获得的数据进行拟合得到。J–C模型未考虑应变、应变率和温度场之间相互耦合的作用，而这种耦合作用对高速加工来说又非常突出。因此，Andrade等[76]提出了修正J–C模型。

3.1.2 切屑分离准则的确定

切屑分离准则选取不当，可能会导致仿真过程不收敛甚至失败。目前广泛采用的分离准则有两类。（1）几何准则[77]，判断切削路径上刀尖点与位于刀尖点前单元之间的距离是否达到事先设定的临界值。一旦达到，该节点就会断裂分离成两个节点，一个随切屑继续流动，另一个则保留在工件表面。（2）物理准则[78]，以等效塑性应变、断裂应力、应变能密度等物理变量作为实现切屑与工件基体分离的标准。当刀尖点处的物理变量达到设定的临界值时，单元节点发生分离，即生成切屑。两者相比较，几何分离准则精度较低，通用性较差。

3.1.3 网格划分

目前，有限元模型网格划分技术主要有：修正拉格朗日算法[79]、欧拉算法[80]、自适应拉格朗日–欧拉算法[81]和欧拉–拉格朗日综合法[82]。不同的网格划分技术有不同的应用场合，具体应用时应酌情考虑。网格划分在整个仿真过程中具有重要作用，主要包括3部分内容： （1）定义网格密度，为节省仿真时间，可对局部区域进行网格细化； （2）设置网格控制属性； （3）设置合适的单元类型。

3.1.4 刀屑接触摩擦模型

切削过程中，刀具和工件之间会发生剧烈的摩擦，包括流动切屑与前刀面之间的摩擦以及后刀面与已加工表面之间的摩擦。设置准确的接触摩擦系数对切削力、刀具磨损、切削温度的预测具有重要意义。根据ZOREV提出的黏结–滑动摩擦模型，刀–屑接触区域分为黏结部分和滑动部分，认为黏结区的剪应力为固定值，等于材料的屈服应力；滑动区摩擦系数为常数，满足库仑摩擦定律[73]，即

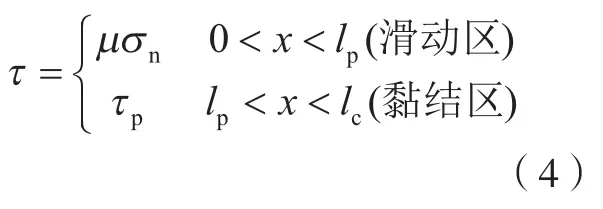
式中，σn为法向应力；τp为剪切应力；μ为摩擦系数。

3.2 切削过程有限元仿真应用研究

3.2.1 切屑形态仿真

金属切削过程与切屑的形成紧密相连，研究切屑形成机理有助于通过参数优化减少刀具磨损、提高加工质量、降低加工成本。在切削过程中，锯齿状切屑对切削力、切削区温度场和工件表面质量产生严重影响[83]，因此，锯齿状切屑的形成机理及其对切削过程的影响已经成为这一领域的研究热点。

Jomaa等[84]采用有限元揭示了高速切削AL7075–T651过程中锯齿状切屑的形成机理，发现刀尖处局部剪切应变向自由表面扩展是锯齿状切屑形成的首因。基于断裂能理论，Zhang等[85]实现了切屑形貌预测，并分析了切削速度、摩擦系数和刀具前角等的影响。为揭示刀尖圆弧半径对切屑形貌的影响，Zhang等[86]利用Abaqus/Explicit建立了三维切削模型。岳彩旭等[87]通过有限元仿真分析了锋利刀刃、倒圆刀刃和倒棱刀刃对锯齿切屑形成过程的影响，仿真结果显示刃口形式对切削过程的影响显著。

鉴于切屑的形成与材料的损伤和扩展紧密联系，而应力、应变、应变率和温度等因素决定了损伤的萌生。因此，如何更为合理地选用断裂准则来描述切屑形成仍有待更深入研究。

3.2.2 切削力与切削温度仿真

有限元分析作为一种有效的工具，被广泛应用于切削力与切削温度预测。Özel[88]采用DEFORM–2D实现了硬质合金刀具切削模具钢的切削力与切削温度预测。沈雪红等[89]借助Abaqus模拟了车削钛合金过程中切削力和切削温度场的变化规律，并得到了试验验证。张京京等[90]提出了一种人工热电偶和有限元热仿真相结合的刀尖温度测量方法，为刀尖温度测量提供了一种可靠的新方法。Ng等[91]对硬态切削过程中的切削温度和切削力进行了有限元仿真，为切削条件的优化提供了有力的支撑工具。

由上可知，尽管切削力与切削温度的预测已经取得了一定的成果，但仍有一些问题亟须解决，主要集中在摩擦模型的构建和选取、刀具涂层热力学参数的匹配以及热传导与热损耗问题上。

3.2.3 刀具磨损仿真

鉴于刀具磨损直接影响零件的加工质量，预测刀具磨损对于实现刀具切削性能最大化和生产成本最小化至关重要。Attanasio等[92]将构建的基于磨粒–扩散机制的刀具磨损模型以子程序方式嵌入到三维有限元仿真软件中，对车削 AISI 1040过程中的刀具磨损进行了准确预测。Özel等[93]研究了多涂层刀具对加工 Ti–6Al–4V 的影响，通过刀具磨损仿真的研究为刀具涂层的优化提供了理论依据。马廉洁等[94]使用DEFORM研究了切削速度、切削深度和刀具路径对刀具磨损的影响，发现刀具磨损分为3个阶段。

由上可知，通过有限元仿真揭示刀具在切削过程中的磨损特性对于提高工件质量、降低加工成本和优化工艺参数具有重要意义。

3.2.4 残余应力仿真

以残余应力为代表的表面完整性指标对零件的功能与使用寿命有很大影响。残余应力试验测量存在一定困难，因此利用有限元仿真来研究残余应力不失为一种可取的方法。

Arrazola等[95]通过建立三维车削模型，采用任意拉格朗日–欧拉法自适应网格划分，实现了残余应力预测并得到试验验证。Özel等[96]通过建立三维有限元模型，对 Ti–6Al–4V和IN 100进行了车削仿真，研究了刀具几何参数和涂层对残余应力分布的影响，发现压应力随刃口半径的增加而增大，而使用涂层刀具时，加工表面残余应力逐渐向拉应力转变。Lazoglu等[97]提出了一个增强型分析模型，该模型考虑了工件上热应力和机械应力叠加，可快速获得进给方向上的残余应力分布。唐水源等[98]将切削过程等效为接触正应力、剪应力和热流量在加工表面的循环作用来模拟预测车削表面残余应力的分布。

迄今，有关残余应力的切削仿真研究很多，也得出了一些有意义的结论。残余应力的产生和分布规律与切削过程工件的塑性变形及温度场息息相关，但刀具的磨损程度直接影响到塑性变形程度和温度场的梯度分布，进而影响残余应力的分布规律。因此，如何准确模拟出刀具磨损过程中残余应力场的分布，对零件的疲劳寿命预测具有重要意义。

4 面向数控切削加工过程的数字孪生技术

数字孪生 （Digital twin，DT）建立在虚拟仿真基础上，由Grieves[99]提出，其核心理念是构建一座连接虚实世界的双向通道。传统的数字仿真关注的是模型能否准确反映物理对象的特性与状态，而数字孪生则重点关注物理对象的动态变化。Tao等[100]率先将数字孪生引入到智能制造领域，并提出了数字孪生车间概念。迄今，有关数字孪生技术在制造领域的研究主要聚焦于如何用数字孪生思想去提升制造业智能化水平。Schleich等[101]提出了一种虚拟表面模型，模型附加了零件的设计、工艺和测量信息，以便与制造过程中的真实零件关联。Lu等[102]对数字孪生技术在制造系统和制造过程的最新进展进行了综述，并重点分析了“工业4.0”背景下的数字孪生智能制造的内涵、应用场景和研究热点。Zhu等[103]提出了一种面向薄壁零件制造的数字孪生框架 （图9），该框架由生产准备、加工和测量3部分构成，并由数字孪生技术驱动，将不同的状态、不同的制造信息和数据进行集成，以供机床操作者和其他数字孪生系统使用。

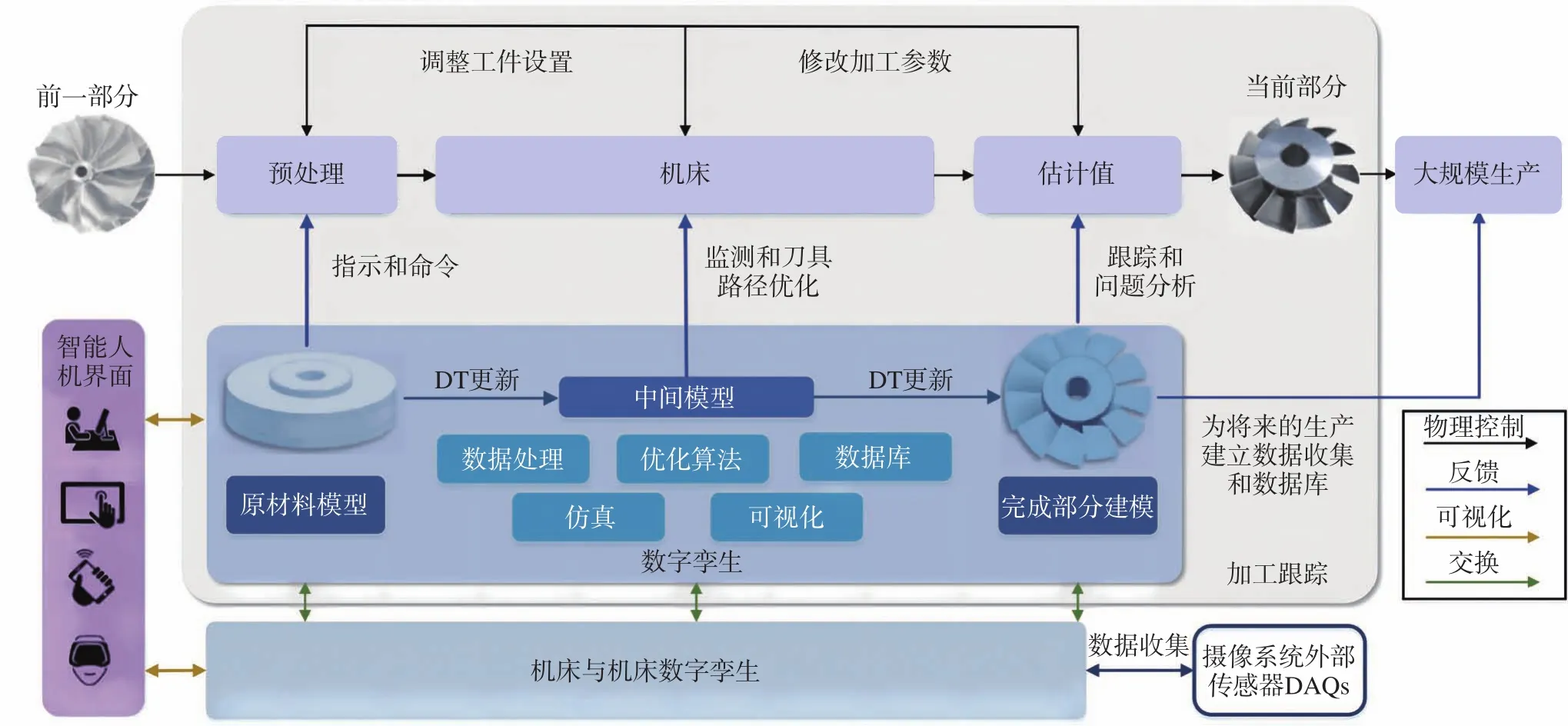
图9 面向薄壁零件制造的加工过程数字孪生框架[103]Fig.9 Digital twin frame of machining process for thin-walled parts manufacturing[103]

作为一种新型的虚实融合方式，数字孪生技术在切削过程仿真的基础上，能够实现与真实切削加工过程的同步运行，并从中获取切削加工过程真实参数，以便在虚拟环境中实现智能加工。一个典型的数控加工大数据与数控机床孪生系统实例如图10所示[104]。下面将从智能化的角度对面向数控切削加工过程的数字孪生技术的4个关键要素进行探讨[105]。

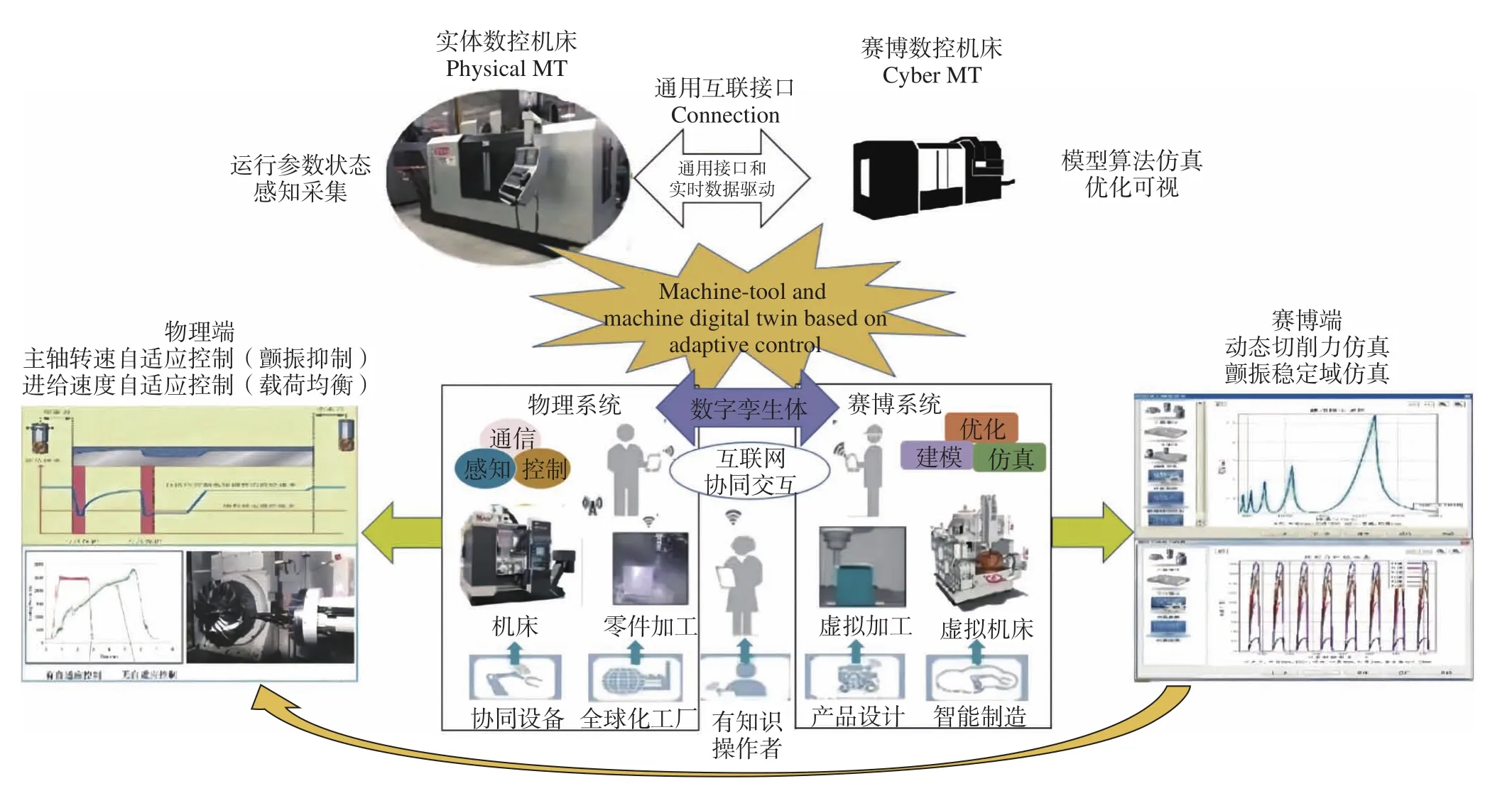
图10 数控加工大数据与数控机床数字孪生系统实例[104]Fig.10 Example of digital twin system of CNC machining big data and CNC machine tool[104]

4.1 智能感知

智能感知是指数控机床对加工过程状态、参数和效果的感知能力。它通过安装在数控机床上的传感器（如位移、速度、加速度、电流、温度和声发射等）及其感知技术去感知加工过程参数与状态信号，经由统一的数据接口，并以标准协议的形式存储在统一的数据库中。

跨硬件平台的统一数据接口是实现智能感知的关键。目前，数字化车间通常配备了不同类型的数控设备。数控系统的封闭性导致来自不同厂商的设备具有不同的接口，给加工过程参数的采集带来了不便。MTConnect是一种用于实现机床各功能部件互联互通的标准化通信协议，用它来传输数据，不失为一种可行的解决方案。在零件加工过程中，CNC系统将以一定的频率把刀具位置、主轴转速、进给速度、切削力和系统状态码等加工状态数据发送给虚拟环境，以便进行虚拟加工仿真及加工状态评估。

4.2 智能理解

获取完整的加工工艺信息并深入理解加工任务与目的，是实现智能加工的数字基础。例如，在进行型腔铣削时，数控系统所感知的只是由G代码表示的简单运动指令，要实现智能理解就必须有一套完善的加工工艺描述规范。STEP–NC标准采用一种语义化并符合面向对象的组织结构，来构建CAD、CAM与CNC之间的全要素信息共享模型，故可担当此任。基于STEP–NC标准的加工工艺模型，以树状结构的形式对诸如加工计划、加工特征、加工工步、刀具几何与切削参数等加工过程信息进行组织，既方便定位到与某个加工特征相关的参数，也便于理解其加工行为。模型中包含的刀具位置信息，通过相应的后置处理可以生成适合不同数控系统的G/M代码，以便独立于特定的硬件设备。

4.3 智能推理

智能推理是指利用智能感知得到的加工过程数据以及智能理解得到的模型，推理出包括零件的几何形状、尺寸精度、表面形貌和加工进度等在内的工件实时加工状态数据，体现为虚拟仿真与加工过程信息推理。虚拟仿真环境可实现刀具几何模型、刀具轨迹、零件和机床模型的三维可视化显示，是数字孪生系统的核心。由于仿真由数控系统输出的刀位数据驱动，并随加工过程而动态变换，可展示被加工毛坯的几何形态。虚拟仿真环境还可以提供诸如切削力预测、颤振预测、刀具磨损预测以及加工表面形貌预测等。例如，利用主轴转速、主轴振动及切削噪声等智能感知信号，可以对切削颤振进行实时预测。

4.4 智能服务

智能服务指数字孪生系统可对来自机器或用户的个性化需求做出反应。通过实时数据的双向互联，用物理世界智能感知到的数据提升虚拟仿真精度，将虚拟仿真数据反馈给物理世界优化加工工艺，循环迭代从而提升服务质量[104]。以工业机器人智能服务模型为例，它结合加工仿真与工步检测功能，可自动分析机床的运行状态，在机床开始加工前或完成加工后，自动向机器人发送上下料指令，并自动规划运动轨迹，控制其执行相应动作，免除人工干预，节约成本。

5 展望

本文结合国内外研究现状，从切削过程建模、切削力预测、切削过程稳定性分析、切削过程有限元分析、面向切削过程的数字孪生技术等方面对切削加工过程物理建模与仿真的相关技术进行了深入探讨与分析，介绍了其实现的基本原理和基本步骤，归纳总结出各自的特点与应用场合。目前，尽管这些领域在理论研究和工程应用等方面已经取得了显著进步，但也应该注意到，这一领域的研究仍面临较大的困难与挑战，有待在以下几方面进行深入研究。

（1）切削过程动力学建模与模型求解是切削力预测和稳定性分析的关键，该领域面临的挑战主要有：如何构建能真实反映切削加工过程的动力学模型；如何采用有效的方法求解时变、非线性、时滞切削动力学方程，揭示其中蕴含的动力学现象的本质；如何构建考虑非线性过程阻尼的切削过程动力学模型并求解，以解决低速阶段稳定性预测不准确的难题。

（2）刀具磨损、切削材料与切削方式的改变以及系统的动态特性等都会改变材料的切削力系数；系统动态特性受到刀具装夹状况、材料不断切除及主轴转速改变等因素影响。现有获取切削力系数及加工系统动态特性所采用的辨识方法均存在一些不足。因此，有必要采用基于数据驱动和有限元分析相结合的方法，建立更为精准的理论模型，根据影响因素的变化，自动修正系统的动态特性及切削力系数，以便更加准确、高效地进行动态切削力预测及切削稳定性分析。

（3）现有的颤振预测技术主要依赖于建立复杂的物理模型，但模型缺乏普遍性和自适应性。因此，有必要针对不同的机床、刀具、工件材料及夹具组合，建立颤振数据库，借用机器学习和深度学习等人工智能理论与技术，实现颤振的智能预测，并在此基础上实现颤振数据库的智能进化与完善。

（4）目前大多数有限元仿真是通过二维模型预测的，鉴于加工过程中的工件和刀具大多具有三维几何特征，为深入揭示切削机理，建立符合实际切削条件的三维有限元仿真模型，综合考虑多因素的影响，将是未来发展方向。

（5）可靠的材料接触模型和材料本构模型是有限元仿真成败的关键因素，材料属性应能准确地反映切削状态下材料的力学性能。新材料的不断涌现，客观上迫切需求不断探索新的材料本构模型。

（6）表面完整性是机械加工关注的重点领域，其产生机理非常复杂，融合了多学科的理论与技术。加强表面完整性有限元仿真研究，寻找各工艺因素对表面完整性的影响规律，探索通过工艺优化提高零件表面质量和使用寿命的技术途径。

（7）考虑到加工零件的复杂性、工厂制造环境和制造条件的多变性，构建全面的工件制造过程和数控机床数字孪生系统，目前仍然是一项巨大的挑战。需要在切削加工机理、先进传感器及其融合技术、虚实模型交互与同步、仿真的准确性与实时性、智能优化算法等方面有新的突破。

（8）目前的数字孪生系统仅能起到智能监控作用，尚无法控制机床运行。开发智能数控系统，用智能数控系统代替机床终端，并实现更高级别的数字孪生系统，实现智能制造，将是未来的发展方向。