Mecanum 轮式全向移动平台的开发研究

段运雄

（中国煤炭科工集团上海有限公司，上海，200030）

0 引言

传统移动平台只能实现两个自由度的运动，在运动学上其等同于传统的陆上车辆，在狭窄空间内转弯作业时有很大的局限性。Mecanum 轮式移动平台具备三自由度的运动能力，可在保持自身姿态不变的前提下，进行正向、横向、斜向的移动和任意半径的旋转，充分增加了移动平台的机动性能[1-2]。

1 Mecanum 轮参数化设计

Mecanum 轮式移动平台之所以能够完成全向移动，在于其轮子的特殊性，每个轮毂外沿均分布有多个小辊子，小辊子在跟随轮毂滚动的同时也能够绕本身的轴旋转。小辊子与轮毂两轴线成一定夹角，轮子转动时能够将部分转动力矩传递到小辊子的法线方向，这使得Mecanum轮在地面摩擦力的作用下具有斜向运动的能力[3]。多个Mecanum 轮之间转动配合就能够生成任意方向的力矩，从而实现移动平台三自由度的全向运动。

理论上讲，为了防止轮子运动时产生振动，就要求在任何时候小辊子都要与运动平面相接触，并且轮毂的轴线与地面的距离要保持为定值，于是就要求所有的小辊子沿轮毂形成的包络面正好是Mecanum 轮与地面接触的外圆柱面[4]。

利用SolidWorks 软件对Mecanum 轮进行参数建模，其中小辊子母线可以通过方程式驱动曲线生成。模型建立如图2 所示。

2 移动平台运动学建模

本文对全向移动平台进行运动学方程推导，首先对平台的运动情况作出如下假设[5]：

1）假设运动地面平整、无阻碍；

2）运动过程中，摩擦力足够大，车轮无打滑现象；

3）移动平台整体视为刚体，车体、车轮等均无变形情况；

4）Mecanum 轮与地面接触点的位置关系不变，接触点一直保持在车轮轮心正下方位置最远处。

然后，以移动平台整体作为研究对象，建立如图4所示坐标系，其中，C 点为移动平台中心， 为轮毂中心，为移动平台中心的速度， 表示平台中心点C 到轮毂中心点 的向量， 表示小辊子偏置角。

根据以上坐标系，建立各点的运动速度关系式：

依据式（17）和（18）可推导出全向移动平台的正向、逆向运动学方程如下。

其正向运动学方程为：

3 移动控制方案设计

移动平台控制系统选用STM32 单片机作为主控制板的核心控制单元，通过定时器输出4 路PWM 脉冲信号，独立控制4 个步进电机的转动[7]，利用Mecanum 轮之间的不同转向、转速的配合，实现全向移动平台3 个自由度的运动。控制系统方案如图6 所示。

平台运动控制模式的设计分为手动操作模式和位移控制模式，其中手动操作模式下可通过触控屏手动控制平台进行正向、横向、斜向和原地旋转4 种运动，运动速度可进行慢速、中速和快速的设置；位移控制模式则是通过输入x、y 坐标值和θ角速度来控制平台的运动。两种控制模式设计界面如图7 所示。

当上位机设置好运动控制模式后，控制模块将4 个轮子的PWM 脉冲信号和转向信号发送到电机驱动模块，由电机驱动器将电脉冲信号转换为角位移，驱动步进电机转动，再经过减速机减速传递到Mecanum 轮，从而实现全向移动平台的运动。

4 虚拟样机仿真分析

基于ADAMS 软件建立移动平台的虚拟样机，根据4个Mecanum 轮与车体之间以及各个小辊子与轮毂之间的运动关系，定义各个运动副、几何约束关系以及各接触之间的摩擦关系[8]。

通过车轮与车体之间增添4 个旋转驱动来模拟运动电机，驱动移动平台进行各项运动[9]。虚拟样机共定义了1 个固定约束（f ixed joint）、40 个旋转副（revolute joint）、36 个接触副（contact）和4 个旋转驱动（rotational joint motion），虚拟样机模型建立如图8 所示。

建立虚拟空间坐标系O-xyz，移动方向取各坐标轴正方向为正向，负方向为反向，旋转方向取顺时针方向旋转为正向，逆时针方向旋转为反向。规定沿x 轴轴线方向的平面移动为正向运动，沿y 轴轴线方向的平面移动为横向运动，既有正向运动又有横向运动定义为斜向运动，沿z 轴轴线的转动为旋转运动。

样机4 个车轮的转速以及仿真时长依次按照表1 进行设置。

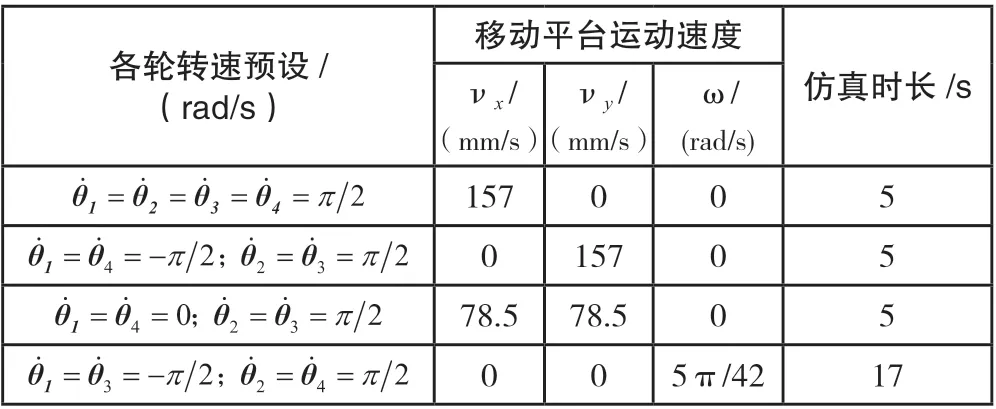
表1 移动平台运动速度和各轮转速

仿真完成后，可得到移动平台位移和速度的相关响应曲线，如图9 所示。其中，由(a)图可以看出，正向运动中移动平台沿x 轴正方向位移呈线性增加，速度νx经起步加速后稳定在157mm/s，而沿y轴方向位移量为0，速度νy保持为0mm/s；由(b)图可以看出，横向运动与正向运动相反，沿x 轴方向位移量为0，速度νx为0mm/s，而沿y轴正方向位移呈线性增加，νy经过加速之后稳定在157mm/s，但相比正向运动，横向运动的速度稍显波动，这是由于仿真中Mecanum 轮与地面打滑和振动引起的[10]；(c)图可以看出，斜向运动中移动平台沿x、y轴正方向位移曲线均呈线性增加，且基本吻合，速度νx、νy经过加速之后均稳定在78.5mm/s 附近，移动平台沿x、y轴正向45°斜向运动。

图9 中的(d)图分别是移动平台在原地旋转运动仿真中平台中心沿x、y 轴方向位移曲线、线速度状态曲线和沿z 轴的角速度状态曲线，可以看出，平台旋转仿真一个周期内沿x、y 轴方向存在±2mm 范围内的微小偏移，周期末回到位置原点，偏移量较小车尺寸可忽略不计。沿x、y 轴方向的线速度维持在0mm/s，有±5mm/s范围的速度波动，沿z 轴的旋转角速度ω经加速后维持在21.4(。/s)≈5π/42(rad/s)。

5 样机调试和运动性能检测

本文试验方案的设计：在实验室空旷平整的地面设置5 个标记点位置，其中4 个标记点位置以1.3m×1.3m呈标准正方形布置，剩下的1 个标记点位置标记在正方形正中心位置。通过在事先标定好距离的位置点之间对全向移动平台进行正向运动、横向运动、斜向运动和原地旋转，验证平台的运动性能，试验方案如图10 所示。

具体操作过程是：首先在手动操作模式下将全向移动平台移动到指定位置，并调整位姿，验证手动操作控制的准确性。之后切换到位移控制模式，进行该模式下的调试与检测。测试过程中，移动平台由初始位置开始，如图10（a）所示，沿平台位移坐标系x 轴负方向移动（横向运动），位移参数输入为 ，运动到达第二位置点，如图10（c）所示；然后沿平台位移坐标系y 轴负方向移动（正向运动），位移参数输入为 ，运动到达第三位置点，如图10（e）所示；接下来沿平台位移坐标系第一象限斜向45°方向移动（斜向运动），位移参数输入为，运动达到第四位置点，如图10（g）所示；最后移动平台进行原地旋转90°，运动参数输入为 ，平台最终位姿状态如图10（i）所示。

经过多次试验，全向移动平台都能准确到达各个目标位置，且最终平台的位姿相同。

6 总结

1）本文阐述了Mecanum 轮式移动平台的全向运动机理，通过小辊子母线的参数方程，利用SolidWorks 对Mecanum 轮进行了参数化设计；

2）推导了Mecanum 轮式全向移动平台的一般运动学方程，对本文研究的移动平台进行了运动学模型的创建；

3）对全向移动平台控制方案进行了设计，基于ADAMS 软件创建移动平台虚拟样机，并分别对平台的正向、横向、斜向和原地旋转运动方式进行了仿真分析；

4）对研究的样机进行调试和运动性能检测，试验证明本文研究的Mecanum 轮式全向移动平台在两种控制模式下均能稳定进行3 个自由度的运动，符合预期设计要求。