融合自适应权重与Levy 飞行的拉丁超立方体海鸥优化算法及应用

梁静

（贵州大学 大数据与信息工程学院，贵阳 550025）

0 引言

近年来，随着群智能优化算法的发展与应用，越来越多的优化算法也陆续得以提出，例如蜻蜓算法（Dragonfly algorithm，DA）［1］、蝴蝶优化算法（butterfly optimization algorithm，BOA）［2］、灰狼优化算法（Grey Wolf Optimization，GWO）［3］、水循环算法（Water Cycle algorithm，WCA）［4］、樽海鞘算法（Slap swarm algorithm，SSA）［5］、鲸鱼优化算法（Whale Optimization algorithm，WOA）［6］、黏菌优化算法（Slime mould algorithm，SMA）［7］等。这些通过模仿自然界中生物规律来构建不同搜索机制的群智能算法，被广泛运用到各种优化问题中去寻找最优解或者次优解。

Dhiman 等人［8］受海鸥迁徙行为以及迁徙过程中觅食行为的启发，在2019 年提出海鸥优化算法（Seagull optimization algorithm，SOA）。在SOA 算法中，海鸥的迁徙行为代表算法的全局搜索能力，觅食行为则代表算法的局部开发能力。该算法原理简单，在工业问题以及分类问题上部署难度低。虽然SOA 算法在一些方面表现优异，但是海鸥的群体觅食行为会降低算法的多样性以及算法搜索能力，此外该算法还存在收敛速度慢，容易陷入局部最优等缺陷。针对这些问题，文献［9］引入记忆功能提高海鸥算法的搜索能力以及规避局部最优的能力。文献［10］利用混沌初始化、多方向飞行路径等策略改进算法，增加算法的多样性与寻优能力。文献［11］引入自适应t分布变异策略，提高算法跳出局部最优的能力。文献［12］使用Sigmoid函数与黄金正弦机制引导海鸥完成搜寻以及位置更新，提高算法的收敛速度和精度。

上述改进策略对该算法的多样性、寻优精度以及收敛速度等方面均有一定的提升，为了进一步提高该算法的性能并检验该算法在实际应用中的效果，本文提出了融合自适应权重与Levy 飞行的拉丁超立方体海鸥优化算法。首先，采用拉丁超立方体抽样的方法产生海鸥种群的初始位置，使海鸥种群在空间上分布更加均匀、避免碰撞，能够加快海鸥寻找目标的速度；其次，在海鸥迁徙阶段引入自适应权重因子，有利于算法在当前位置使用精确的搜索策略，加快算法收敛；最后，在海鸥觅食阶段使用Levy飞行策略［13］，使个体位置变化更加灵活多样，提高算法的多样性与跳出局部最优的能力。本文使用23 个基准测试函数和图像分割问题检验改进算法的效果，并将实验结果与原算法以及其它优化算法做比较，验证了ALLSOA 算法的先进性。

1 海鸥优化算法

海鸥优化算法是通过模拟海鸥2 个最重要的特征：迁徙和觅食而提出的算法。海鸥是群居生活动物，在季节更替时，海鸥会进行迁徙活动。迁徙时海鸥会保证自己的位置与其它海鸥的位置不同，避免发生碰撞。海鸥是杂食动物，在觅食时会以螺旋形的运动形态攻击其它候鸟。海鸥的迁徙行为与觅食行为可以用以下数学模型来表示。

1.1 迁徙

在该过程中，算法模拟海鸥从当前位置移动到下一个位置。在移动过程中，海鸥会满足3 个条件：避免碰撞，最佳位置方向，靠近最佳位置。

为了避免碰撞，算法通过添加变量A来计算海鸥的新位置。对此可表示：

其中，Cs（t）表示不与其它海鸥发生碰撞的新位置；Ps（t）表示海鸥当前的位置；t表示当前迭代数；fc表示控制A的频率，取值为2；Maxiteration表示最大迭代次数。

满足避免碰撞的条件之后，海鸥会向最佳位置方向运动。研究推出的数学公式可写为：

其中，Ms（t）表示最佳位置方向；Pbs（t）表示海鸥的最优位置；rd是［0，1］内的随机数。

在海鸥确定最佳位置方向后，就会向该方向移动，到达最佳位置。数学公式具体如下：

其中，Ds（t）表示海鸥的最佳位置。

1.2 觅食

海鸥在觅食过程中会以螺旋形运动状态攻击猎物，因此海鸥在x、y、z平面中的数学模型如下：

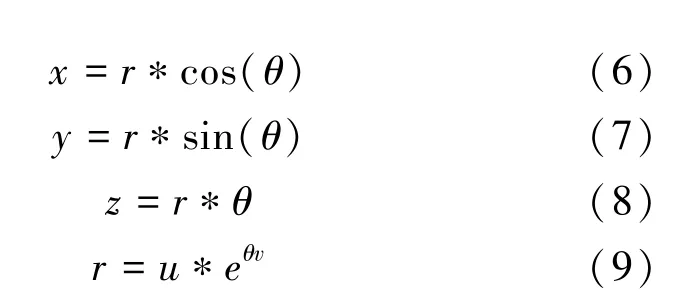
其中，r表示螺旋半径；[0，2π] 是 [0，2π] 内的随机数；u为常数。

因此，海鸥觅食行为的数学描述为：

其中，Ps（t）表示海鸥当前攻击的位置；Ds（t -1）表示海鸥上一时刻的位置；Pbs（t -1）表示海鸥上一时刻的最优位置。

2 融合自适应权重与Levy 飞行的拉丁超立方体海鸥优化算法

2.1 拉丁超立方体初始化

海鸥算法的初始化方法是在规定界限内随机生成海鸥的位置，这种初始化方法很容易导致海鸥个体在空间中分布不均，进而影响算法的寻优精度。为解决该问题，本文采用拉丁超立方体抽样的方法初始化种群。

拉丁超立方体抽样的关键是将输入概率分布进行分层，在每一层中抽取一个样本。这样可以保证海鸥初始位置的分布更加均匀，避免早熟。拉丁超立方体抽样的步骤如下：

Step 1确定抽样规模H，即海鸥种群规模。

Step 2将每个海鸥位置变量di的定义域区间划分为H个相等的小区间，即：

Step 3生成H × n的矩阵A，其中每列均为数列1，2，…，H的随机排序。

Step 4A的每行对应一个超立方体，每个超立方体产生一个样本。

初始化位置分布如图1 所示。由图1（a）可知，随机初始化位置在上半部比较密集，下半部比较稀疏；图1（b）中位置分布则比较均匀。因此可以得出，使用超立方体初始化种群相较于随机初始化种群位置分布更为均匀，更有利于算法寻优。

图1 初始化位置分布图Fig.1 Map of initializing the location

2.2 自适应权重因子

在标准的海鸥算法中，海鸥的位置更新公式主要是由海鸥当前位置、最佳方向与随机参数组成。随机参数的大小对算法的搜索能力、寻优能力都有着较大的影响。因为当该参数越大时，海鸥位置更新的步长越大，算法对全局搜索的能力越强；当这个参数越小时，海鸥位置更新的步长越小，算法对局部的搜索能力越强。但是海鸥算法中该参数是随机生成的，这将导致该算法在计算海鸥个体位置时盲目性较高，无法很好地分配算法在初期与末期的搜索能力。

针对该问题，本文在海鸥算法的群体行为中加入自适应权重因子。在更新最佳位置方向时，使用自适应权重因子代替海鸥算法中的随机数。自适应权重因子的数学表达式为：

在海鸥算法的位置更新中引入自适应权重因子的个体位置更新公式为：

算法迭代开始时，自适应权重因子最大，海鸥个体位置更新步长最大，代表算法此时的全局搜索能力最强。此后，自适应权重因子随着时间的增大而减小，海鸥个体位置更新步长逐渐减小，代表算法的局部搜索能力逐渐加强。

2.3 Levy 飞行

Levy 飞行模拟自然界中动物觅食的游走过程，并且服从莱维分布，是一种短距离搜索与长距离行走相间的飞行方式。这种飞行机制由法国数学家莱维提出，可以用来缓解海鸥算法早熟的问题以及增加算法的多样性。Levy 飞行的数学表达式为：

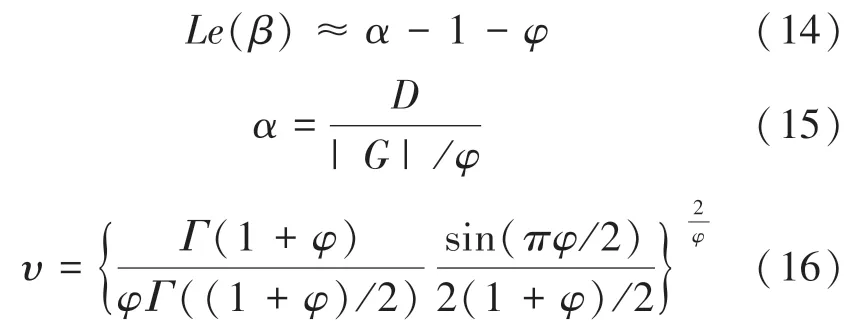
其中，0＜φ≤2；D、G～N（0，υ）；Γ（x）是Gamma 函数；α表示步长；φ＝2／3。

使用Levy 飞行后的海鸥位置更新部分的公式更新为：

其中，rand为［0，1］之间的随机数。

改进后的位置更新公式，可以使海鸥的位置变化更加灵活，不仅增强算法的寻优能力，还减少算法出现局部最优的现象。

2.4 ALLSOA 算法步骤

结合上述改进方法，本文研发的ALLSOA 算法伪代码的设计表述见如下。begin设置初始参数：种群规模N，超参数fc，最大迭代次数Maxiteration获取测试函数F的边界与维度信息拉丁超立方体初始化种群，计算种群每个搜索代理的适应度

2.5 时间复杂度计算

算法复杂度是算法运算速度的一种体现，也可以反映出算法的效率。在改进算法时算法的时间复杂度如果变大，将会增加算法的运行时间，降低算法效率。在此，本文比较SOA 算法与ALLSOA 算法的时间复杂度。

SOA 算法的时间复杂度的组成部分是：随机初始化参数O（1），计算适应度O（N），迭代计算最优值O（NT），则SOA算法的时间复杂度为：

其中，N为种群大小，T为迭代次数。

ALLSOA 算法的时间复杂度的组成部分是：拉丁超立方体初始化参数O（NT），计算适应度O（N），迭代计算最优值O（NT），自适应权重因子O（NT），Levy 飞行O（NT），故ALLSOA 的时间复杂度如式（19）所示：

其中，N为种群大小，T为迭代次数。

综上，本文改进后的算法ALLSOA 时间复杂度与原算法相比未见增加，故ALLSOA 算法的改进部分并未影响到算法的计算效率。

3 图像分割

本文使用不同的智能算法对K-means 聚类算法［14］进行优化，并使用各算法的最优解完成图像分割任务。

K-means 聚类算法的主要思想是将给定的样本集，按照样本个体之间的距离大小将样本划分为规定的簇数，令簇内的点尽量连接紧密，簇间距离尽量远。根据聚类中心分簇的度量方式为平方差：

其中，x（i）为样本点；a（i）是与x（i）最相似的类别；yj为聚类中心。

使用智能算法优化K-means 聚类算法进行图像分割的步骤为：

Step 1加载图像，将图像像素点转化为样本数据。

Step 2初始化簇心。

Step 3使用智能算法优化K-means 聚类算法，更新簇心坐标，计算样本数据与簇心的距离，取距离最小簇心的类作为该样本的类别。

Step 4计算更新后的簇心坐标与当前簇心坐标的差距，若大于规定阈值，重复Step3，反之结束。

4 仿真实验与结果分析

4.1 实验环境与参数设置

本文实验运行环境为：64 位Windows10 操作系统，Intel Corei5-7300HQ 的处理器，Matlab R2020b的仿真软件。

为验证ALLSOA 算法的性能与图像分割效果，分别进行了2 种实验。实验1 使用23 个基准函数检验ALLSOA 的算法性能并与其它算法做比较；实验2 使用图像分割案例验证ALLSOA 的先进性，并与其它算法做比较。23 个基准函数见表1，前7 个函数为单峰值函数，其余为多峰值函数。

4.2 算法性能对比实验

为了检验本文算法的性能，本文选择了不同的智能优化算法：鲸鱼优化算法（WOA）、樽海鞘优化算法（SSA）、标准海鸥优化算法（SOA）以及改进算法（ALLSOA）进行对比实验。为了提高实验的准确性，对每个智能优化算法进行30 次独立实验后，取实验结果的平均值与标准差进行对比。本次实验设置参数为：种群规模N＝30，最大迭代次数T＝1 000。实验结果见表2，加粗字体表示4 种算法求解的最优解。

由表2 可知，ALLSOA 求解函数f1、f2、f7、f8、f15、f19的最优值时，比其它优化算法差一点。但是对于函数f8，ALLSOA 求解的最优值精度虽差，但是标准差更小，算法更加稳定。对于函数f15和f19，ALLSOA求解的最优值与其它算法相差甚微，只是标准差稍大。

表2 测试结果Tab.2 Test results

对于单峰值函数f3～f6，ALLSOA 算法的寻优能力明显高于WOA、SSA 与SOA 算法，收敛精度更高。对于多峰值函数f9～f14，虽然只有函数f9和f11被ALLSOA 算法找到了最优值，但是ALLSOA 算法求解得到值均为4 个算法中的最优解，且明显优于SOA 算法求解值。例如f12函数，ALLSOA 算法的解比SOA 算法的解相差6 个数量级。对于函数f18，虽然4 个算法均找到了最优值，但是ALLSOA 算法的标准差最小。对于函数f20～f23，ALLSOA 在寻优精度与标准差均小于其它3 种算法，与SOA 算法相比有着大幅提升。

综上，实验结果表明ALLSOA 算法相比较其它算法有着较好的寻优能力以及收敛精度，但是在某些函数上的表现并不比其它算法要更好，这也表示海鸥算法还有进一步改进的空间。

图2 给出了ALLSOA 与其它3 种优化算法在求解基准函数最优值时，随着迭代次数的增长，其适应值的变化曲线。从图2 中可以看出，ALLSOA 算法在寻优精度与收敛速度上均优于其它算法。

图2 算法收敛曲线图Fig.2 Convergence curve of the algorithms

4.3 图像分割对比实验

将ALLSOA 算法应用到图像分割中，并与其它2 种算法做对比，实验参数设置为：种群规模N＝30，最大迭代次数T＝50，簇心数Z＝3。

原图与分割后的图像如图3 所示。从图3 中可以明显看出，ALLSOA 算法的分割效果最好，图片中人物与景物的纹理最清晰，最能反映现实景象。

图3 原图与分割图Fig.3 Original image and split images

为了进一步验证ALLSOA 算法在图像分割中的性能，本文绘制3 种算法在分割过程中的收敛曲线如图4 所示。

从图4 中可以看出，ALLSOA 算法的寻优能力与精度均高于其它算法，在迭代第10 次左右时接近收敛，且寻优精度最高。另外，3 种算法的平均运行时间、最佳适应度与初始聚类中心见表3。

图4 WOA、SOA 与ALLSOA 收敛曲线Fig.4 Convergence curves of WOA，SOA and ALLSOA

由表3 得出，ALLSOA 适应度值最低，虽然比WOA 慢0.06 s，但是ALLSOA 解出的最佳适应度比WOA 低159.387，且聚类中心中没有零值，聚类效果更好。

表3 算法运行结果Tab.3 Running results of the algorithms

综合前文研究可知，通过基准函数测试与图像分割测试，均可以证明本文提出的ALLSOA 算法的性能对比其它算法有着较好的提升，具有更好的收敛速度和寻优精度。

5 结束语

本文针对海鸥优化算法（SOA）的各项不足，提出了融合自适应权重与Levy 飞行的拉丁超立方体海鸥优化算法（ALLSOA）。首先，在初始化时利用拉丁超立方体抽样方法让海鸥分布更加均匀，使海鸥更加容易找到最优目标；其次，在海鸥位置更新时引入自适应权重因子，更好地控制算法的全局寻优与局部搜索能力；最后，在海鸥的觅食阶段使用Levy飞行策略，增加海鸥位置的灵动性，提升算法跳出局部最优的能力。通过23 个基准函数和图像分割的仿真实验结果表明，本文提出的算法具有更好的稳定性、寻优能力与收敛精度。

未来的研究方向是进一步提升海鸥算法的收敛精度，并应用于更多的工程问题当中。