一类非线性度较高的拉丁方阵*

董新锋,周 宇,张文政

(保密通信重点实验室,四川成都610041)

一类非线性度较高的拉丁方阵*

董新锋,周 宇,张文政

(保密通信重点实验室,四川成都610041)

拉丁方变换是一类非常重要的变换,在密码算法设计、组合设计等领域具有广泛的应用,目前对密码性质好的拉丁方阵的构造方法研究较少。通过研究基于可逆方阵的多输出Bent函数的构造方法,提出了一种利用本原多项式来构造非线性度高的拉丁方阵的算法,并对这类拉丁方阵的密码性质进行了分析和测试,结果表明这类拉丁方阵具有较高的非线性度和较高的代数次数,能够用于实际应用中密码算法的设计。

拉丁方 多输出Bent函数 非线性度

0 引 言

拉丁方变换是一类非常重要的变换,在密码算法的设计、组合设计等领域中有广泛的应用。例如, 4×4拉丁方变换经常被用于序列密码的设计[1-2]。密码算法设计中使用的拉丁方变换一般要求具有良好的密码学性质,例如高的代数次数、高的非线性度、较小的差分概率等。构造密码学性质好的拉丁方变换以及分析拉丁方变换的密码学性质,对于利用拉丁方变换构造安全高效的密码算法具有重要意义。目前这方面公开的研究成果较少,文献[3]研究了2n阶拉丁方的差分密码特性,考察了差分的概率分布和均值,以及差分表中各种值的平均数,并探讨了这些指标的近似计算问题。文献[4]从多输出布尔函数的给出了拉丁方变换的几个等价刻画描述,并详细讨论了拉丁方变换的Walsh谱特征和差分特征。

本文从多输出布尔函数[5-7]的角度,给出了一种利用2n入n出Bent函数构造n阶拉丁方阵的方法,并给出了测试实例。相关的测试结果表明,这种方法得到的拉丁方阵具有较高的非线性度和较高的代数次数。这种构造方法结构简单,并且能够快速实现,可以用于实际应用中密码算法及协议的设计。

1 准备知识

定义1设f:→,如果对∀a∈都有f(a)∈,则称f是n入m出的多输出布尔函数。

定义2设S:{0,1,…,n-1}→{0,1,…,n-1},如果S恰好是一个置换,则称S是n阶置换。

定义3设L:{0,1,…,2n-1}×{0,1,…,2n-1}→{0,1,…,2n-1},如果∀a∈{0,1,…,2n-1},以x为变量的函数L(a,x)和L(x,a)都是置换函数,则称L是n阶拉丁方变换,相应的2n×2n阶矩阵称为n阶拉丁方阵。

n阶拉丁方变换,等价于2n入n出的多输出布尔函数。因此可以通过研究多输出布尔函数的相关工具来研究拉丁方阵的性质,如通过Walsh谱等工具来刻画拉丁方阵的非线性度、代数次数、相关免疫性质、扩散性质、差分概率等[4]。

n阶拉丁方变换具有以下性质:

性质1：n阶拉丁方变换L具有1阶相关免疫性质。

性质2：对n阶拉丁方阵的所有行进行2n阶置换,得到的矩阵仍然是n阶拉丁方阵。

性质3：对n阶拉丁方阵的所有列进行2n阶置换,得到的矩阵仍然是n阶拉丁方阵。

2 2n入n出Bent函数

根据文献[5]中关于严格M-M类Bent函数的构造方法和结论,容易得到下述引理1～引理3。详细证明过程可参考文献[5],本文不再赘述。

引理1对任意正整数n,存在F2上的n×n阶方阵A,使得{A,A2,A3,…,An}中任何若干个方阵的和矩阵都是可逆方阵。

特别地,对任意正整数n,在F2上有φ(2n-1)/ n个n次本原多项式,此处φ(·)表示欧拉函数。取任意n次本原多项式1+a1X+a2X2+…+an-1Xn-1+Xn,则下面的矩阵A满足引理1中的要求。

引理2设A是F2上的n×n阶可逆方阵,则y=xA是→的置换函数,其中x=(x1,x2,…,xn)∈。

引理3设A是F2上的n×n阶方阵,且满足{A,A2,A3,…,An}中任何若干个方阵的和矩阵都是可逆方阵,则{g1(x)=xA,g2(x)=xA2,…,gn(x)= xAn}中任何若干个函数的和函数都是置换函数。

由引理1～引理3,容易得到下面2n入n出Bent函数的构造方法。

构造方法1:设A是F2上的n×n阶方阵,且满足{A,A2,A3,…,An}中任何若干个方阵的和矩阵都是可逆方阵,则可定义2n入n出Bent函数h(x,y)形式如下:

3 n阶拉丁方阵

定理1：设h(x,y)为构造方法1中构造的2n入n出的Bent函数,且满足h(x,x)是n入n出的置换函数,则可通过h(x,y)构造高非线性度的拉丁方阵L。

证明:能够通过n阶高非线性度拉丁方阵的构造算法Alg_construct_Latin(n)来证明该定理,即给出了定理1的构造性证明。

算法Alg_construct_Latin(n):

输入:任意正整数n,n次本原多项式1+a1X+a2X2+…+an-1Xn-1+Xn。

输出:n阶拉丁方阵L。

具体步骤如下:

Step1对任意正整数n,取定一个n次本原多项式1+a1X+a2X2+…+an-1Xn-1+Xn,生成对应的特征矩阵

Step2基于n阶矩阵A构造{A,A2,A3,…,An},进而构造{g1(x)=xA,g2(x)=xA2,…,gn(x)= xAn},其中x∈,gj(x)∈,j∈{1,2,…,n};

Step3构造2n入n出Bent函数h(x,y)= g1(x)y1+g2(x)y2+…+gn(x)yn,其中y=(y1,y2,…,yn)∈,并将h(x,y)表示成2n×2n阶矩阵

Step4将2n阶矩阵h对角线上的元素h(x,x)与第一行的对应元素h(0,x)和第一列的对应元素h(x,0)交换得到拉丁方阵

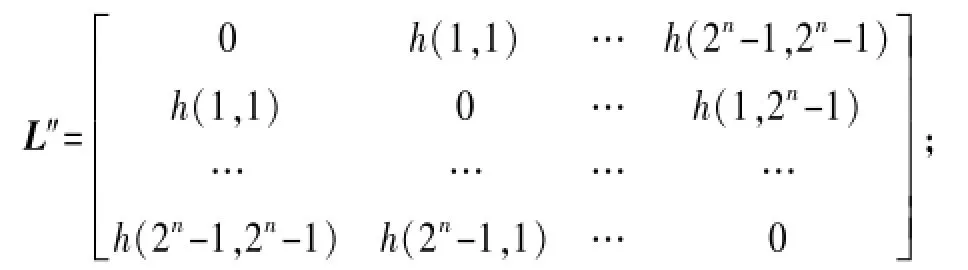
Step5对L″的所有行进行2n阶置换S1得到拉丁方阵L′,对L′的所有列进行2n阶置换S2得到拉丁方阵L。

注:步骤Step3中取定h(x,y)中的分量x=m≠0或y=m≠0时,h(m,y)或h(x,m)均为置换函数;当m=0时有h(x,0)=h(0,x)=0。由于h(x,x)是n入n出的置换函数,因此步骤step4中交换元素后能得到拉丁方阵L″。

推论1：算法Alg_construct_Latin(n)中构造的n阶拉丁方阵L″的非线性度满足

证明:2n入n出Bent函数的非线性度为22n-1-2n-1。算法Alg_construct_Latin(n)的步骤Step4中总共改变了Bent函数h(x,y)的3×(2n-1)个值,且相应的分量函数在第1行、第1列及对角线上分别改变了2n-1个值。根据非线性度的定义,nl(L″)与Bent函数h(x,y)的非线性度22n-1-2n-1相比至多下降3×2n-1,即得到n阶拉丁方阵L″的非线性度下界22n-1-2n-1-3×2n-1=22n-1-2n+1。

推论2：算法Alg_construct_Latin(n)构造的n阶拉丁方阵至少有φ(2n-1)/n个。

证明:由算法Alg_construct_Latin(n)的步骤Step1易知构造的n阶拉丁方阵个数至少与n次本原多项式的个数相同,即φ(2n-1)/n。

下面我们给出具体的构造实例和测试结果。

例设n=4,构造4阶拉丁方阵L。

Step1 选择的4次本原多项式为1+X3+X4,对应的特征矩阵

得到的8入4出Bent函数h(x0x1x2x3,x4x5x6x7)的16×16阶真值表矩阵h为(十六进制):

Step4 将矩阵h对角线上的元素与第一行和第一列的对应元素交换得到4阶拉丁方阵L″为(十六进制):

Step5 对L″的所有行进行16阶置换S1得到拉丁方L′,对L′的所有列进行16阶置换S2得到拉丁方阵L:

对上述的Bent函数h、拉丁方阵L″、拉丁方阵L分别进行整体非线性度、代数式次数、最大差分概率等密码性质的测试。

详细测试结果见表1。

表1 矩阵的密码性质Table 1 Cryptographic properties of matrix

表1中的测试结果表明:通过算法Alg_construct_Latin(n)得到的4阶拉丁方L具有良好的密码性能,L的整体非线性度为96,代数式次数为6,能够被用于实际密码算法的设计。

4 结 语

本文通过研究多输出Bent函数,给出了一种构造非线性度较高的拉丁方阵的算法,并对实例的主要密码性能进行了测试,相关测试结果表明,该类拉丁方具有良好的密码性能,如高的非线性度、高的代数式次数等,能够被应用于实际密码算法的设计。

如何设计其他密码性质好的拉丁方阵以及如何通过更一般的多输出布尔函数来构造拉丁方变换是需要继续深入研究的问题,对设计密码性质好的拉丁方阵具有重要意义。

[1] 陶仁骥.(4,4)拉丁阵在密码设计上的一种应用[J].计算机学报,1991(14):423-451.

TAO Ren-ji.An Application Of(4,4)-Latin Arrays To Cryptography[J].Chinese Journal Of Computers,1991, (14):423-451.

[2] 熊玲,申兵,王金波.有限域小波变换的密码学性质简评[J].通信技术,2013,46(12):58-61.

XIONG Ling,SHEN Bing,WANG Jin-bo.Review on Cryptographic Property of Finite-Field Wavelet Transform [J].Communications Technology,2013,46(12):58-61.

[3] 曾国平.拉丁方的差分分布特性研究[J].计算机工程与设计,2009,30(06):1376-1378.

ZENG Guo-ping.Differential Distributions of Latin Squares.Computer Engineering And Design,2009,30 (6):1376-1378.

[4] 金晨辉.拉丁方变换的几个等价刻划[J].通信学报, 2003,24(06):139-132.

JIN Chen-hui.Equivalent Characteristics For Latin Square Transformations[J].Journal Of China Institute Of Communication,2003,24(6):139-132.

[5] Takashi Satoh,Tetsu Iwata,Kaoru Kurosawa.On Cryptographically Secure Vectorial Boolean Functions[C]// International Conference on the Theory and Applications of Cryptology and Information Security,Singapore,Proceedings of Advances in Cryptology-ASIACRYPT'99. [s.l.]:Springer,1999:20-28.

[6] CESMELIOGLU A,MEIDL W.A Construction of Bent Functions from Plateaued Functions[J].Designs,Codes and Cryptography,2013,66(1-3):231-242.

[7] STANICA P,MARTINSEN T,GANGOPADHYAY S,et al.Bent and Generalized Bent Boolean Functions[J].Designs,Codes and Cryptography,2013,69(01):77-94.

DONG Xin-feng(1985-),male,M.Sci., engineer,mainly working at cryptology.

周 宇(1980—),男,博士,高级工程师,主要研究方向为密码学;

ZHOU Yu(1980-),male,Ph.D.,senior engineer,mainly working at cryptology.

张文政(1966—),男,硕士,研究员,主要研究方向为密码学。

ZHANG Wen-zheng(1966-),male,M.Sci.,research fellow,mainly working at cryptology.

A Class of Latin Square with Higher Nonlinearity

DONG Xin-feng,ZHOU Yu,ZHANG Wen-zheng
(Key Laboratory of Privacy Communication,Chengdu Sichuan 610041,China)

Latin square,as an important transformation,is widely used in some applications,including cryptographic algorithm design and combinational design.At present,less study is done on the methods to construct Latin squares with good cryptographic properties.By studying the construction method of vectorial bent function based on invertible square and with primitive polynomial,a method to construct Latin squares with high nonlinearity is proposed.Meanwhile these Latin squares are analyzed and the primary cryptographic properties tested,including nonlinearity and algebraic degree.The experiment results show that the Latin square is of good nonlinearity and high algebraic degree,and could be used to design cryptographic algorithm with many applications.

latin square;vectorial bent function;nonlinearity

TN 918.1

A

1002-0802(2014)09-1058-04

10.3969/j.issn.1002-0802.2014.09.016

董新锋(1985—),男,硕士,工程师,主要研究方向为密码学;

2014-05-15;

2014-07-16 Received date：2014-05-15;Revised date：2014-07-16

国家自然科学基金(No.61309034)

Foundation Item：National Science Foundation of China(No.61309034)