梁柱平齐端板连接节点研究
2022-12-11洪绍正
洪绍正,梁 中,张 霰
(1.长江精工钢结构(集团)股份有限公司,安徽 六安 237161;2.南宁市建筑规划设计集团有限公司,广西 南宁 530000;3.安徽省电力公司经济技术研究院,安徽 合肥 230022)
0 引 言
在传统的钢结构建筑分析与设计中,通常假定节点为完全刚性或理想铰接,但实际工程中,节点的刚度处于两者之间,为半刚性连接,所以,这种简化计算不能准确反映实际情况,有时会导致较大的计算误差。早在20世纪90年代,AISC明确规定节点必须考虑半刚性的影响,之后,Bjorhovde等[1]对M-θr进行无量纲化,将连接分为刚性、半刚性、柔性;Eurocode 3[2]从承载力和刚度将其分为全强、部分强度和铰接以及刚性、半刚性和柔性。《钢结构设计标准》(GB 50017—2017)[3]提出了直接分析设计法,要求考虑节点连接刚度对钢结构的影响,尤其是大跨度钢结构体系的稳定性分析。然而,目前各国规范对于钢结构半刚性连接的刚度研究较少,仅有Eurocode 3给出了半刚性端板连接的刚度计算公式。在M-θr曲线中,节点的初始刚度为过原点的切线斜率,斜率越大则刚度越强,反之,则柔性显著。在门式刚架、钢框架及高层钢结构中,端板连接因安装拆卸方便、连接刚度大被广泛使用,通常在梁端部焊接端板,并通过高强螺栓与梁柱连接,常见的连接形式包括外伸式、平齐式和内缩式。
国内外针对端板连接做出了大量的试验研究和理论分析,提出了相应的计算方法。Ostrander及Davison等[4,5]通过试验研究端板厚度、柱截面尺寸及加劲肋对端板连接非线性行为的影响,表明当柱翼缘较薄时,增加端板厚度对初始刚度的提高意义不大。Bose等[6]对18个梁柱端板连接进行试验,指出试验的破坏模型与 Eurocode 3预测的情况有较大不同,并建议鉴于初始刚度公式的准确性问题应参照更多的试验结果。 Brown[7]对端板连接进行了试验分析,针对端板连接的初始刚度提出相应的理论公式,并与Eurocode 3对比,主要考虑柱翼缘和端板的变形,简化了计算方法,对于其他部位的刚度贡献通过柔度经验系数体现。吴兆旗等[8]、侯娟等[9]基于板壳力学理论,给出端板连接初始刚度的解析公式。郭兵等[10]对常见的梁柱节点进行单向加载,并给出其简化的计算方法,结果与试验吻合较好。此外,各国学者对端板连接进行了大量的有限元分析,包括研究节点的刚度、承载能力及端板的应力分布。赵华智等[11]、贾连光等[12]采用有限元分析方法研究端板连接的力学性能,表明螺栓直径、端板厚度对节点刚度有一定影响,而当端板厚度较薄时,增加端板厚度能够明显提高初始刚度。柳春阳[13]通过有限元ANSYS模拟平齐端板进行参数分析,包括端板厚度、螺栓至腹板和翼缘的距离及加劲肋厚度等,提出新的计算模型,计算结果较Eurocode 3精确。施刚[14]对8个梁柱连接进行了静力试验,研究端板厚度、螺栓直径、柱腹板加劲肋等因素对端板连接受力性能的影响,再通过ANSYS模拟,与试验验证,分析更多参数的影响,并提出了端板连接的初始刚度模型。
现有对端板连接初始刚度的计算方法主要基于组件法,一般将节点域划分为端板抗弯区、柱翼缘抗弯区、螺栓抗拉区、柱腹板抗剪区、柱腹板抗拉区、柱腹板抗压区,并对各分区提出不同的力学模型,最后将各分区的刚度贡献串联得出整个节点的初始刚度。而本文也是基于组件法,通过有限元及大量的试验数据得出新的端板连接初始刚度模型,并与现有模型进行对比。
1 试验数据搜集
对于半刚性连接,国内外学者进行了大量的试验研究,许多学者针对半刚性连接建立了相应的试验数据库,如Chen和Kishi数据库[15],对不同连接形式的节点进行了分类,以便学者查找。
而本文搜集了从1970年至今的有关数据,见表1,端板连接几何参数意义如图1所示。
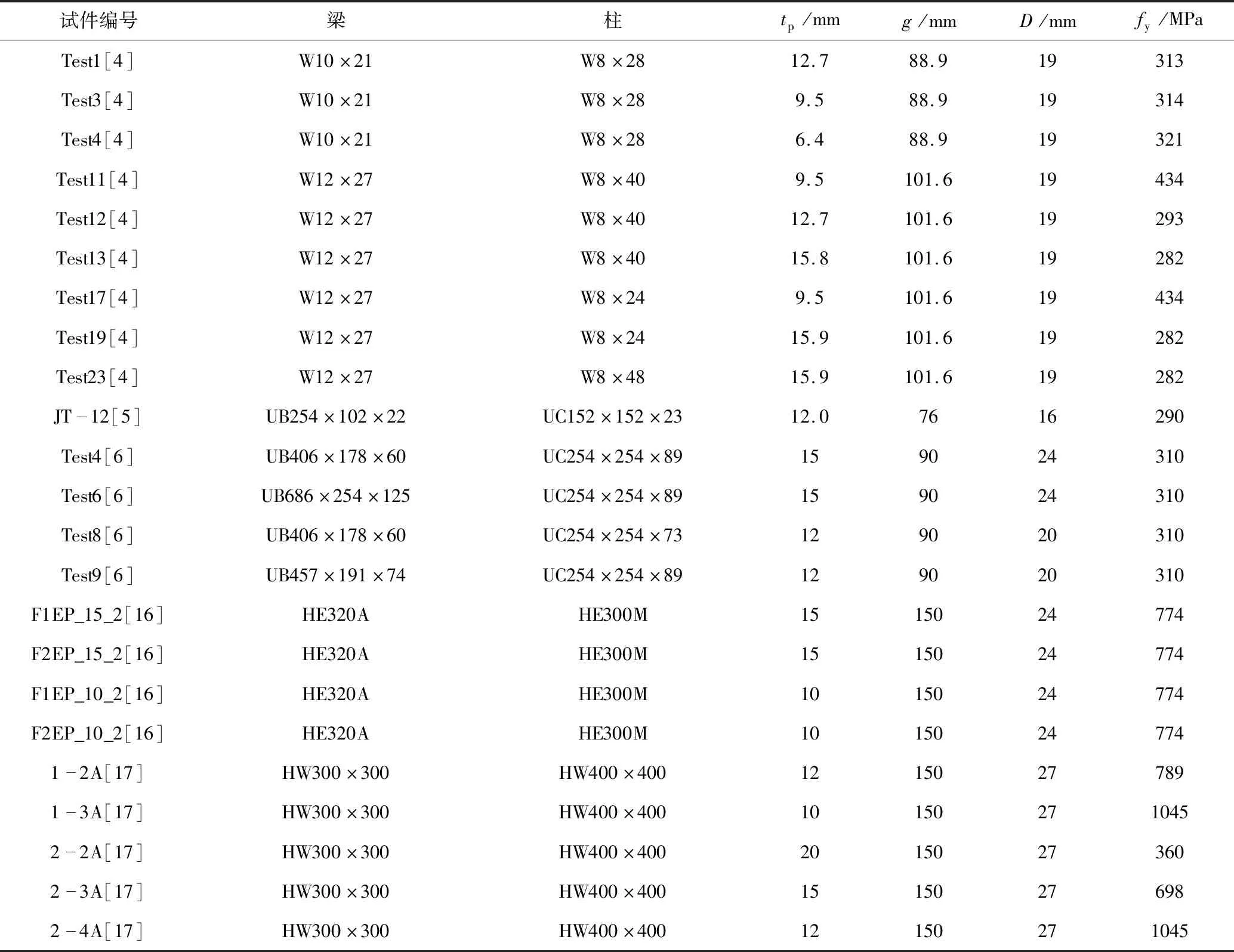
表1 搜集试件几何参数及材料参数
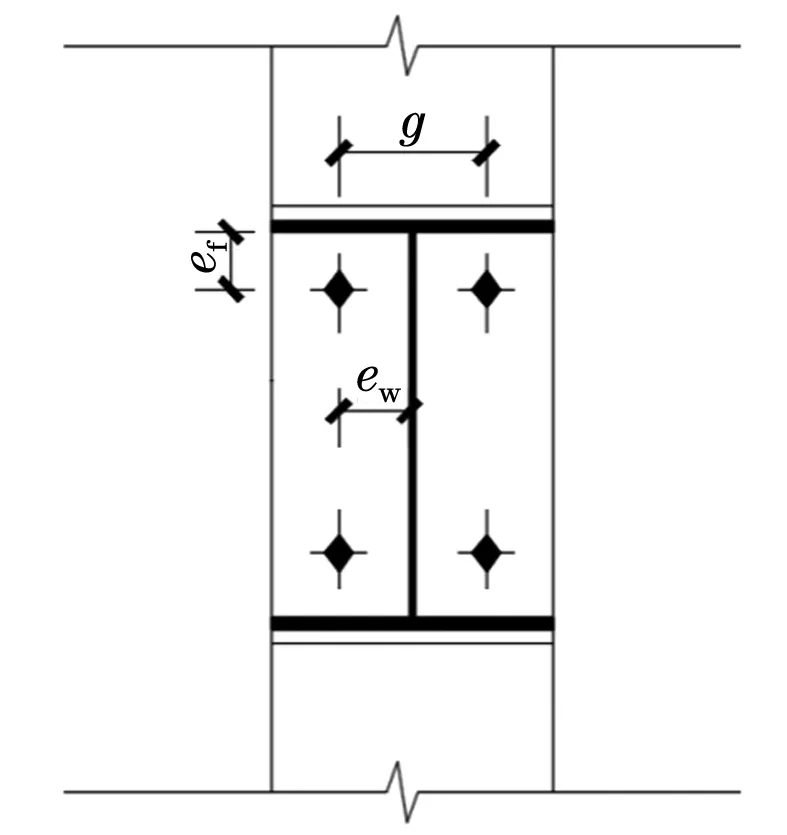
图1 端板连接几何参数
2 有限元分析
2.1 有限元验证
有限元ABAQUS能有效模拟钢节点,为了验证参数分析的正确性,选取了文献[17]四组试件的弯矩-转角曲线,其中梁柱为焊接H型钢,截面尺寸分别为300×300×10×15和428×407×20×35,材料都为Q345,而端板的材料包括Q235、Q345、S690及S960,材料的应力-应变曲线根据文献[17]中试验可得,螺栓为8.8级高强螺栓,直径为27 mm。端板与梁的焊接采用绑定约束,而端板与柱翼缘,螺帽与端板,螺帽与柱翼缘,栓杆与孔壁的接触采用面对面接触,切向摩擦系数为0.44,法向采用“硬”接触。施加荷载作用于参考点上,该参考点与实际梁翼缘表面的荷载作用区域耦合。梁柱的网格划分,对于靠近节点区域的网格进行加密,以提高计算结果的准确性;柱网格划分大小为40,孔壁区域大小为8;梁的网格划分大小为40,连接部位划分大小15;螺栓网格大小为4。所有部件的单元类型为八结点线性六面体单元C3D8R,进行沙漏控制。完成所有接触后,施加荷载时,首先将柱的两端完全固定;再对螺栓施加预紧力,第一步施加10 N的力,第二步施加该螺栓等级的预紧力230 kN,第三步固定螺栓当前的长度,以避免突然施加较大的预紧力导致结果不收敛;完成预紧力的施加,最后采取位移控制对梁施加荷载。建立的有限元模型如图2所示。
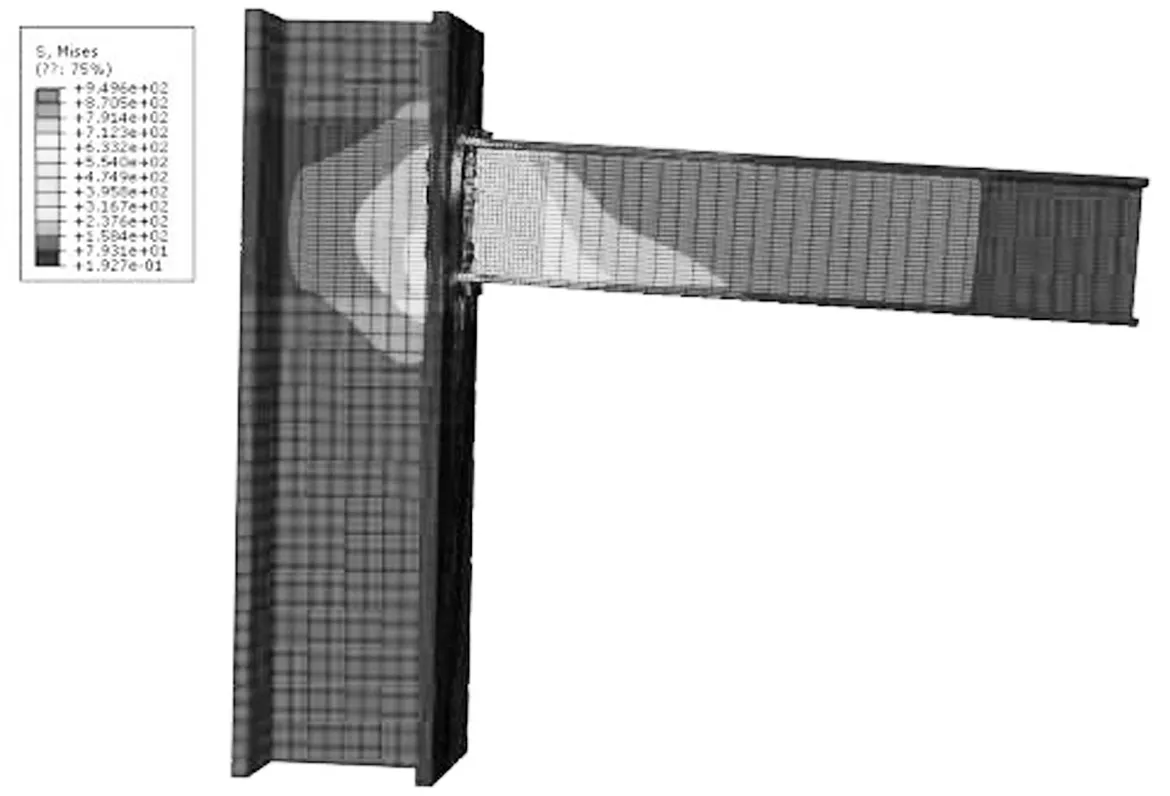
图2 有限元模型
有限元分析对比了文献[17]常温下的1-1A组,2-2A组,1-2A组及2-4A组,验证了该模型可适应于不同钢材的端板,如图3所示。
从图3中可以看出,有限元计算出的弯矩-转角曲线与试验曲线非常接近。这进一步证明了该模型可用于参数分析。
2.2 有限元参数分析
有限元分析的参数,包括端板的厚度tp,分别是6 mm、15 mm、25 mm;端板的屈服强度fy(不同钢材),采用Q235、Q345、S690和S960四种材料;螺栓的直径D,分别为16 mm、22 mm、27 mm;列螺栓之间的距离g分别为90 mm、150 mm、210 mm。各参数分析结果如图4~图7所示。
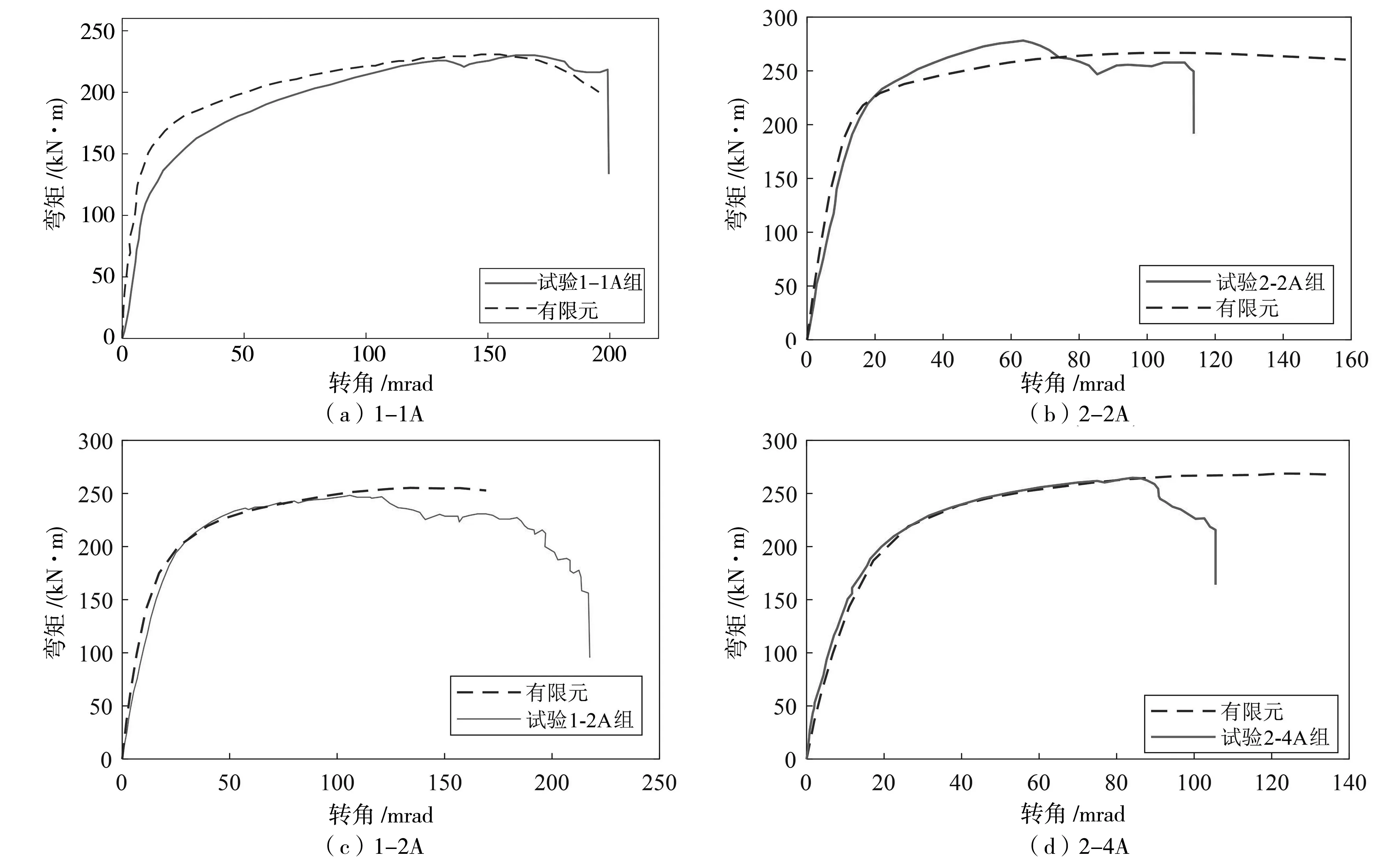
图3 有限元模型验证分析

图4 端板厚度参数分析
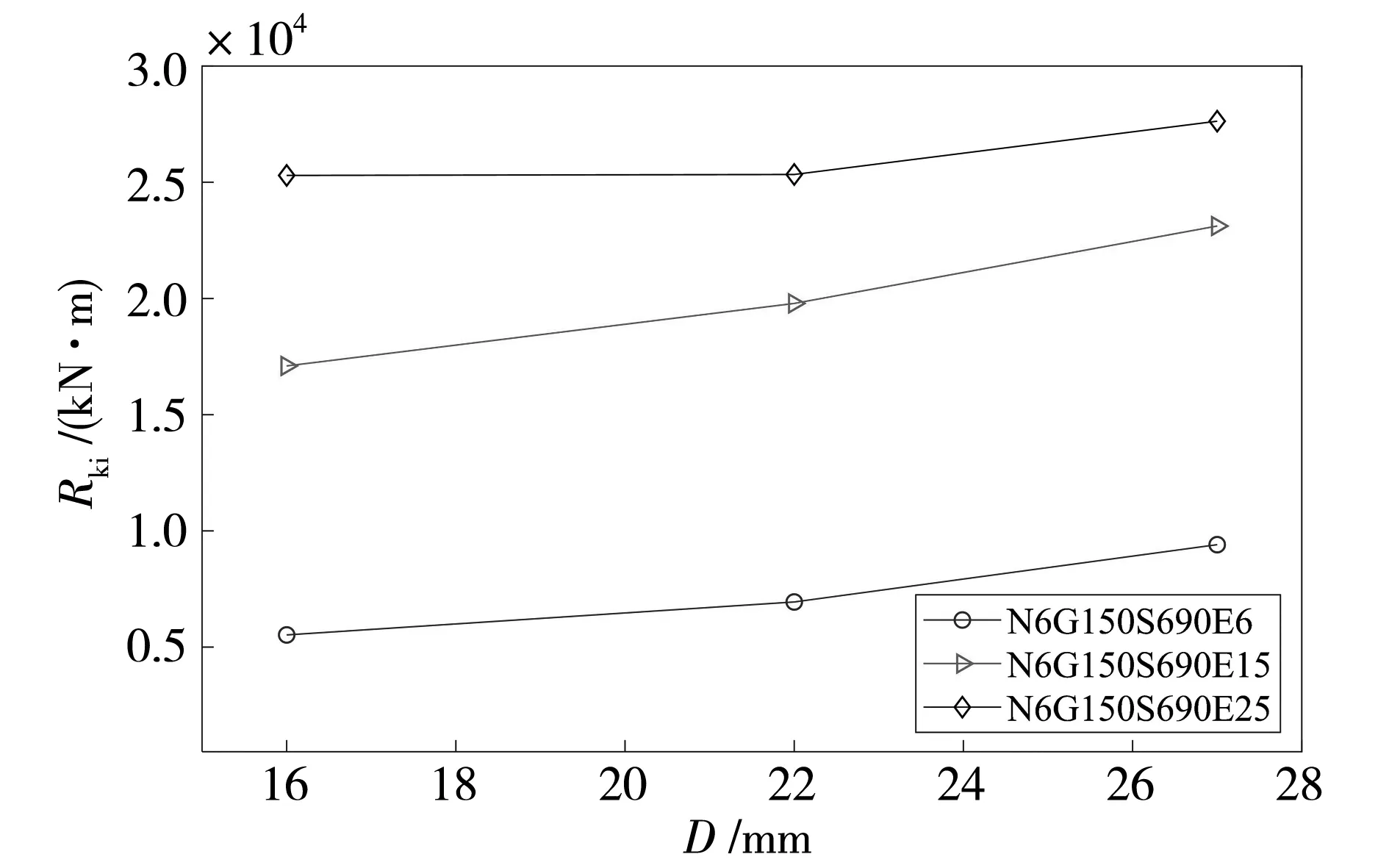
图5 螺栓直径参数分析
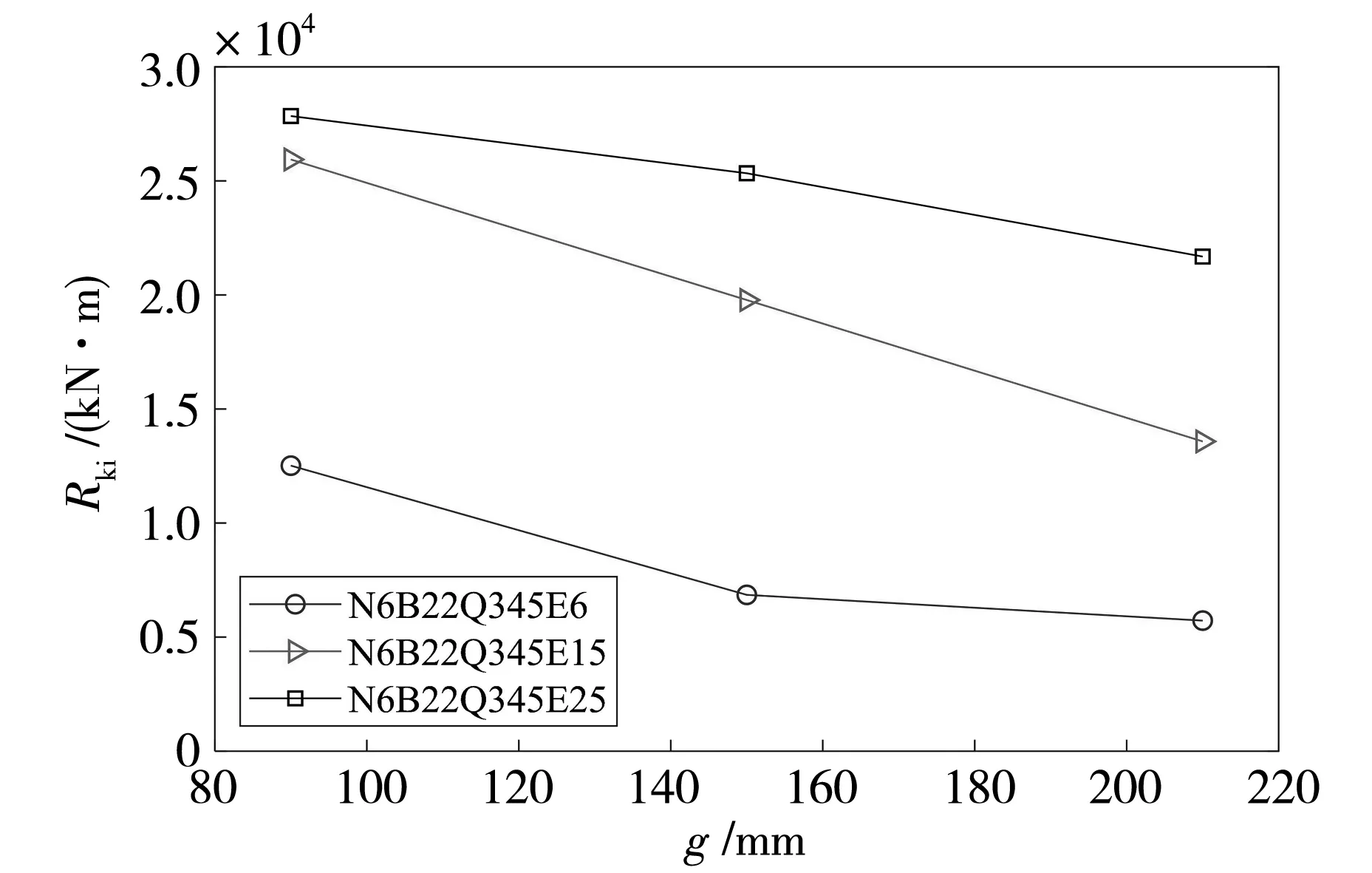
图6 列螺栓参数分析
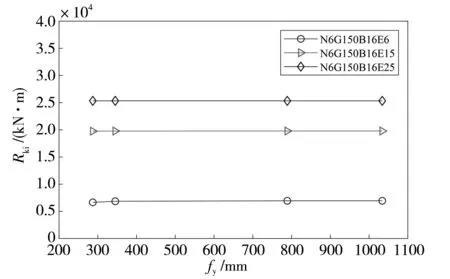
图7 端板屈服强度分析
从图4可以看出,对于相同的列螺栓距离,随着端板厚度增加,节点的初始刚度也增加,但随着列螺栓距离的减小而缓慢增加。例如,列螺栓的距离为210 mm,随着端板厚度增加,初始刚度分别增加137%、596%;而列螺栓的距离为90 mm时,初始刚度分别增加了107%、7%。
从图5可以看出,对于相同条件,随着螺栓直径增大,节点的初始刚度也增大。例如,对于端板厚度为6 mm,随着螺栓直径的增大,初始刚度分别增加了26%、36%。
从图6可以看出,对于相同条件,随着列螺栓距离的增加,节点的初始刚度逐渐减小。例如,对于端板厚15 mm,随着列螺栓距离的增加,节点的初始刚度减低24%、31%。
从图7可以看出,采用不同屈服强度的端板,节点的初始刚度几乎无变化,说明端板屈服强度对节点的初始刚度影响非常小。
综上所述,端板厚度对节点的初始刚度影响最大,螺栓直径及列螺栓距离次之,端板屈服强度影响非常小。
3 初始刚度
3.1 现有的模型
施刚[14]将端板连接分为四个部分来计算,分别为节点域剪切转角、螺栓伸长转角、端板转角及柱受拉翼缘转角。
节点域剪切转角为:
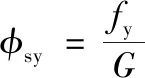
(1)
式中:fy为柱剪切屈服强度;G为剪切模量。
螺栓伸长转角为:
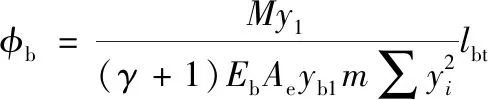
(2)
式中:yb1是第一排螺栓到梁受压翼缘的中心的距离;lbt是螺栓的计算长度,等于所夹钢板厚度加上垫圈厚度;γ是钢板间预压力分布面积与螺栓杆截面积的比值,一般可取10;Eb为螺栓的弹性模量;Ae为螺栓的有效截面面积;yi为每排螺栓至梁受压翼缘中心的距离,m为螺栓的列数。
端板转角为:
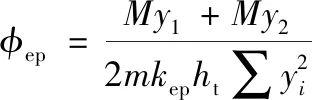
(3)
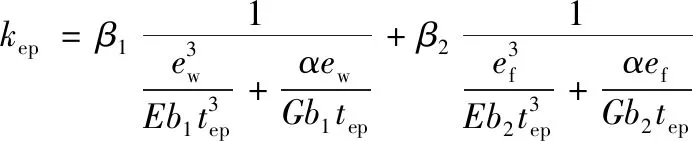
(4)
式中:kep是板段的刚度;ew和ef分别是螺栓中心到梁腹板和梁翼缘的距离;E、G为端板的弹性模量和剪切模量;β1、β2因板段面积重叠,进行刚度折减系数;b1和b2是板段两条固定边的计算长度。
柱受拉翼缘转角与端板的计算方法相同,进行整体分析,带入下式:
φ=φsy+φb+φep+φcf
(5)
最后的节点的初始刚度为:
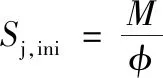
(6)
郭兵等[10]将梁柱节点总初始刚度可分为节点域刚度和连接端板刚度两大部分,最后将二者串联起来得到节点的初始刚度,并给出了计算方法。
节点域的转动刚度为:
Rpz=Ghbhchtcw
(7)
式中:G为柱的剪切模量;hb为梁的高度;hch为柱截面高度;tcw为柱腹板的厚度。
连接端板的转动刚度为:

(8)
式中:E为端板的弹性模量;Ic为端板的惯性矩。
最后节点的初始刚度为:
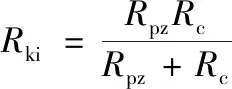
(9)
而Eurocode 3[2]将端板连接视作6个组件构成(component method),即把对连接的强度和变形有重要影响的部分分别看成连接的一个组件,对每一个组件建立力学模型,进行分析计算,最后将所有的组件综合起来对连接进行整体分析计算。
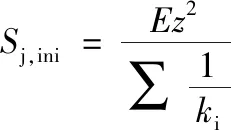
(10)
式中:ki代表第i个组件部分;z是力臂,与连接的类型有关,对于平齐端板连接,取第一排螺栓至梁下翼缘中心的距离。
3.2 建议的模型
本文建议的模型主要考虑节点的端板抗弯区、柱翼缘抗弯区、螺栓抗拉区、柱腹板抗剪区,而对于梁翼缘、梁腹板区不予考虑。
3.2.1 柱腹板抗剪刚度
可根据文献[3],当节点域发生剪切屈服其节点域的抗弯承载力为:
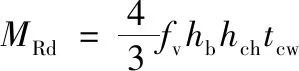
(11)
而节点域的剪切转角为:
φsy=fv/G
(12)
则柱腹板抗剪区的初始转动刚度为:
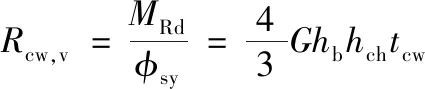
(13)
3.2.2 螺栓抗拉刚度
螺栓受拉产生伸长量,则螺栓的伸长转角为:
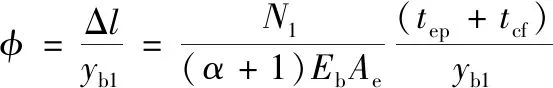
(14)
式中:α根据文献[14]取10,螺栓的计算长度可简化取端板和柱翼缘的厚度,
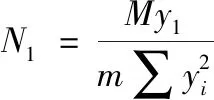
(15)
因为是两列螺栓,所以m=2,则螺栓抗拉的初始刚度为:
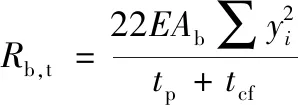
(16)
3.2.3 端板与柱翼缘的抗弯刚度
参照文献[8,9],根据板壳理论,端板与柱翼缘的弯曲转角合为:
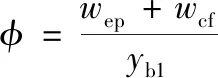
(17)
式中:wep、wcf为受螺栓作用处端板和柱翼缘的挠度,wep=N1/kep,wcf=N1/kcf;N1为作用在螺栓处的荷载,详见下式:
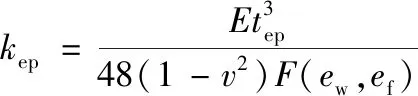
(18)
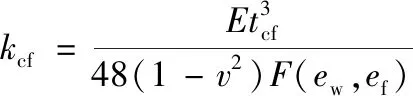
(19)
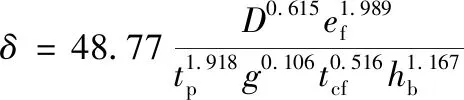
(20)
其中,δ考虑到理论计算与有限元的差异,依据Matlab软件进行拟合得到。最后可得到端板和柱翼缘的抗弯刚度合为:
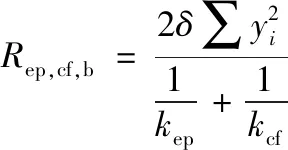
(21)
最后,将上述四个组件串联起来,得到总的初始刚度为:
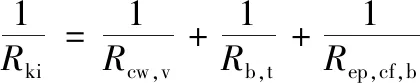
(22)
从表2及图8可以看出,施刚模型平均误差为130.46%,标准差为132.79%,最大误差达438.51%,从图8中可以看出,施刚模型和试验值之间的数据点分散,直线的斜率大于45°,模型理论值总体上大于试验值,可决系数为0.56,说明拟合效果较差;从图9可以看出,郭兵模型平均误差为62.90%,标准差61.26%,最大误差299.36%,直线的斜率远大于45°,可决系数为0.75,计算结果偏于不安全;从图10可以看出,Eurocode 3模型的平均误差为30.08%,标准差为26.97%,最大误差为99.24%,直线斜率也大于45°,理论值较试验值偏大,可决系数为0.877;而从图11可以看出,建议模型平均误差为16.29%,标准差为13.35%,最大误差为42.23%,直线的斜率几乎为45°,说明理论值与试验值非常接近,可决系数为0.97,拟合效果好,能够明显降低误差。
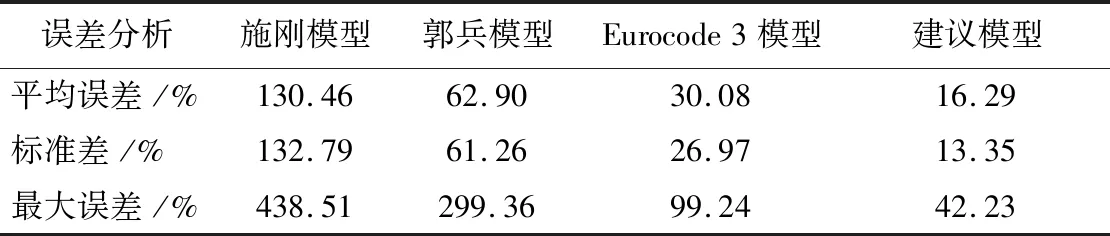
表2 不同模型与试验数据对比
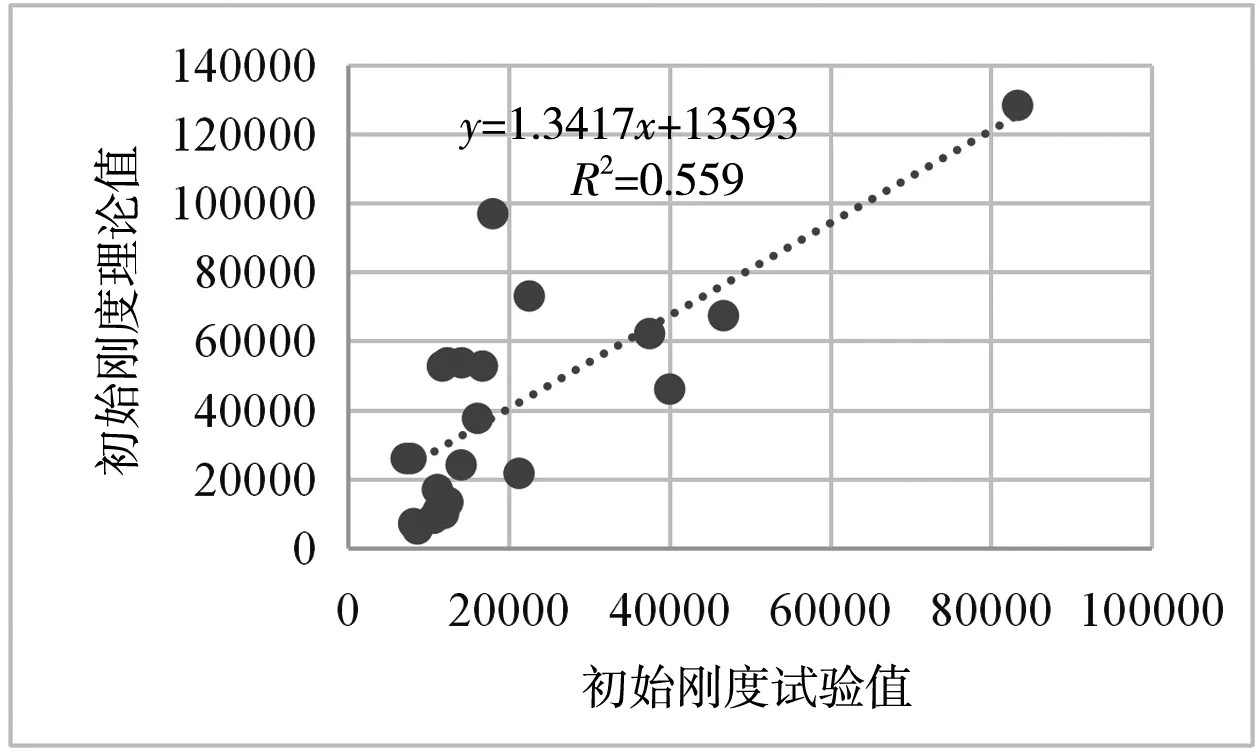
图8 施刚模型误差分析
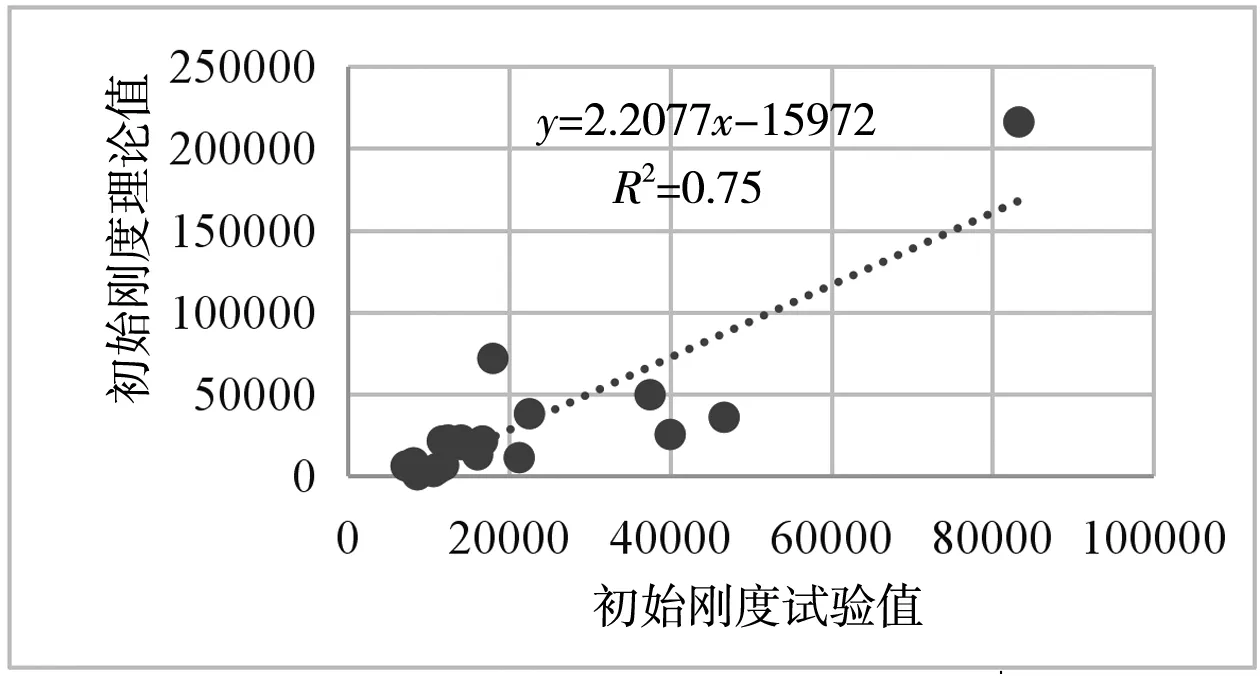
图9 郭兵模型误差分析
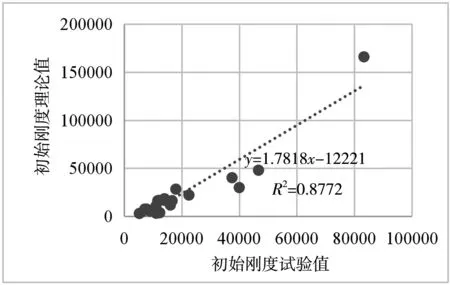
图10 Eurocode 3模型误差分析
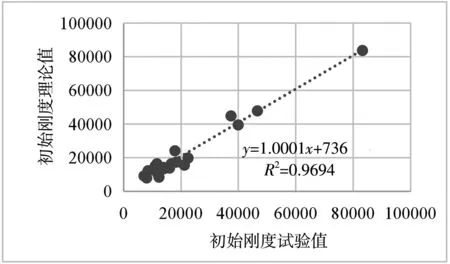
图11 建议模型误差分析
4 结 论
随着列螺栓间距变小,增加端板的厚度,节点的初始刚度增加幅度减小且对节点影响最大,螺栓直径和列螺栓间距次之,端板屈服强度对节点几乎无影响。
基于组件法,不考虑梁翼缘、梁腹板的影响,提出计算平齐端板连接的新模型,并与现有的模型进行对比,平均误差为16.29%,标准差13.35%,最大误差42.23%,能够明显降低误差。
