基于瑞利波的轨道板表面裂缝深度检测方法*

张 尧 张 辉** 朱文发,2 范国鹏 方文平

(1.上海工程技术大学城市轨道交通学院，201620，上海；2.华东理工大学机械与动力工程学院，200240，上海；3.杭州戬威机电科技有限公司，311100，杭州∥第一作者，硕士研究生)

长期服役的轨道板因其混凝土干缩变形和温度变形，易产生表面裂缝。受不均匀沉降、温度变化及列车动荷载的影响，这些裂缝会进一步延伸，逐渐形成深度裂缝甚至是贯穿裂缝。贯穿裂缝处极易发生渗水，不仅会造成钢筋锈蚀，从而导致绝缘节点失效，还可能会导致基床下沉。这些都会影响轨道板的承载能力及其使用功能，成为行车安全的重大隐患[1-5]。可见，在轨道板形成贯穿裂缝前及时进行检测尤为重要，其中较为关键的就是对裂缝损伤程度的判别。

由于铁路路况复杂、外部环境影响大、检测成本较高等因素，轨道板裂缝检测一直是我国高速铁路维护工作的难点。目前，我国轨道板维护主要采取的人工测量判断和记录方法，存在人力成本高、检测时间长、漏检率高、准确率低等问题。近年来，一些研究人员提出了利用图像处理技术对轨道板裂缝进行检测的方法。但是，基于图像处理的检测方法仅能判断裂缝的存在及裂缝定位，无法精确检测裂缝的深度。而且，由于采集图像时缺少自然光，或轨道板长年经受风吹雨淋致使背景颜色有差异等环境原因，现有算法对轨道板的裂缝检测效果并不理想。

为能更加高效且精确地检测轨道板裂缝，本文提出了利用瑞利波的传播规律对轨道板表面裂缝进行检测的方法。

1 瑞利波的基本理论

在均匀介质的表面施加激励时，激励点附近的质点会发生振动。这些质点的振动随后会以应力波的形式传递给相邻的质点，从而导致相邻的质点随之振动，依次循环。在介质内部，这种振动会不断得扩散，产生以激励点为中心的弹性应力波。按照传播特性的不同，这种弹性应力波通常可分为瑞利波与体波。体波在介质的内部传播，可分为纵波(即压缩波)和横波(即剪切波)。瑞利波沿介质表面传播，于1887年由英国学者瑞利发现并验证。瑞利波通常分布在介质的自由表面。在各向同性的均匀介质中，瑞利波传播时的相速度和群速度保持一致。如图1所示的二维平面中，当瑞利波在介质自由表面传播时，质点振动的位移随深度的增加而逐渐衰减[6]。

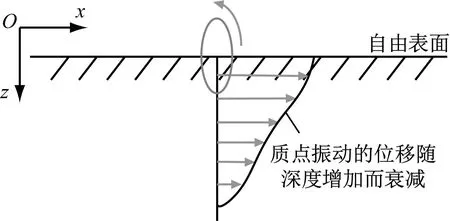
图1 二维平面中的瑞利波传播示意图

由弹性波的理论可知，弹性波的传播速度与弹性介质的泊松比有关。为了方便实际应用分析，根据弹性力学相关知识及理论推导，可以得出纵波、横波及瑞利波的波速与介质的弹性参数有如下关系：

(1)

(2)

(3)

式中：

ρ——密度；

μ——泊松比；

λ——拉梅系数；

G——剪切模量；

vp——纵波波速；

vS——横波波速；

vR——瑞利波波速；

E——弹性模量。

根据相关理论研究，瑞利波传播时有如下特性：

2)瑞利波在各向同性的均匀弹性介质中传播时，不会出现频散现象，波速也不会因为频率变化而改变。

3)瑞利波在介质表面传播时，其质点振动时的位移轨迹呈椭圆状按逆时针方向运动。

4)当瑞利波遇到裂缝或缺陷等异常体时，其能量会发生变化，并且可能出现传播时间延长的现象。

由于瑞利波具有沿介质表面传播、能量衰减较慢等特性，因此，相较于横波和纵波，瑞利波更适用于轨道板之类大体积结构的表面缺陷检测。

2 含表面裂缝的轨道板二维模型

受限于实体试验条件，无法获取轨道板裂缝的现场检测数据，故本文仅采用有限元模型方法进行验证。以ABAQUS有限元软件为平台，建立含有表面裂缝的轨道板二维有限元模型如图2所示[7]。其中L=600 mm，裂缝的宽度为1 mm，在裂缝的左边缘施加激励，裂缝右侧a=60 mm处接收信号。

注：d为裂缝深度；a为接收点与裂缝右侧边缘的距离。

在轨道板有限元模型中，设定主要材料属性，并结合式(1)—式(3)，计算可得轨道板中相关弹性波波速。相关参数的计算结果如表1所示。

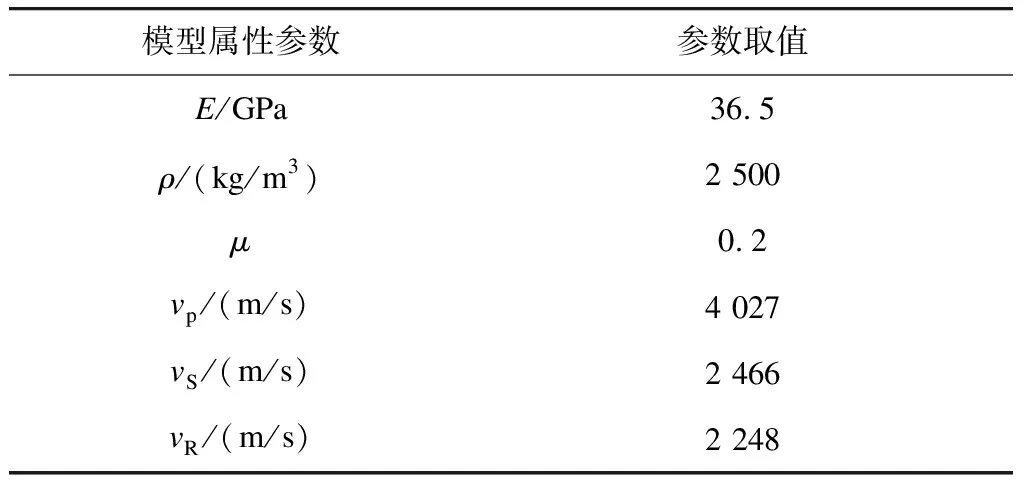
表1 轨道板模型主要属性参数取值

为了满足传播时间差法测量的要求，瑞利波波长需小于裂缝深度，因此需要高频激励源进行激发，以保证瑞利波传播时先经过裂缝的2个侧面，然后到达裂缝右侧的轨道板上表面[8-10]。本研究采用汉宁窗调制的、3个周期的正弦波信号，其中心频率为200 kHz，具体波形如图3所示。对应的瑞利波波长约为10 mm。对模型采用四边形网格进行划分，网格尺寸为1 mm(即约为瑞利波波长的1/10)。

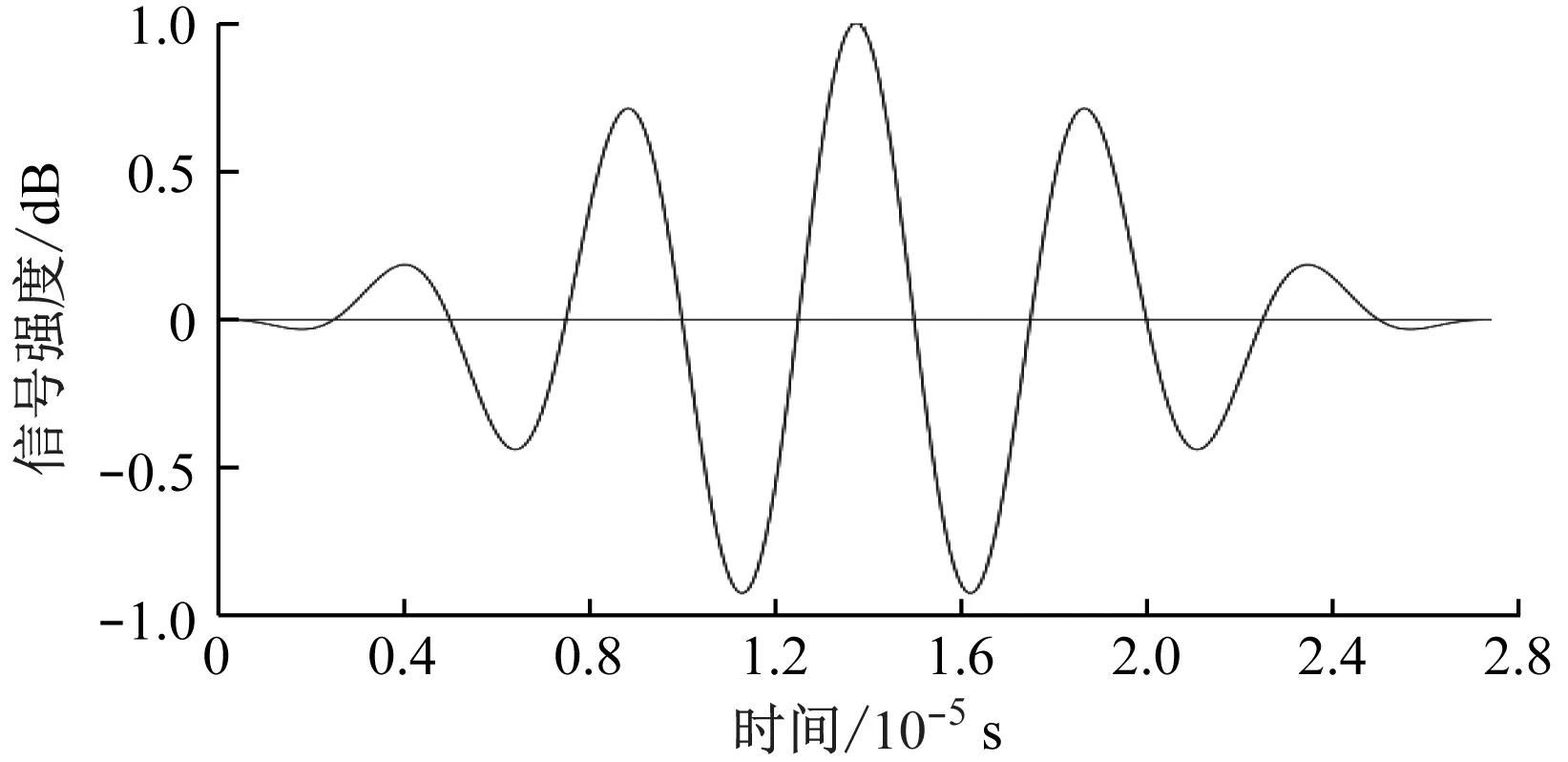
a)信号强度-时间

3 超声波在轨道板中的传播规律

本文选取裂缝深度为60 mm的轨道板二维模型波场云图(见图4)进行定性研究。当时间t=2.0×10-5s时，在激励源的作用下，激发出了纵波、横波及瑞利波3类弹性波。由图4可见，纵波和横波在轨道板内部呈圆弧状扩散，瑞利波则呈地滚式沿着轨道板表面及裂缝左侧表面传播。此外，瑞利波、横波及纵波的能量各不相同。其中，纵波的传播速度最快，且能量较弱；横波和瑞利波的传播速度相差较小；瑞利波的能量较强，明显要高于横波。

图4 t=2.0×10-5s时弹性波激发

如图5所示，当t=4.0×10-5s时，瑞利波沿着裂缝表面传播到裂缝底部。当经过裂缝底端时，部分瑞利波会在此处发生模态转换的现象，通过衍射转换为衍射体波。从图5中能量的变化可以看出，衍射出的体波能量较大。由于此时传播到裂缝底部的瑞利波刚刚发生模态转换，衍射的时间较短，所以很难将衍射体波中的横波和纵波区分出来；其余部分瑞利波则绕过裂缝的底端，向上沿着裂缝的右侧表面继续传播。

图5 t=4.0×10-5s时瑞利波发生模态转换

如图6所示，当t=5.0×10-5s时，经过模态转换后的衍射体波呈圆弧状向轨道板内部四周传播。此时可明显区分转换后的衍射横波和衍射纵波。由于衍射纵波的传播速度较快，故其此时传播的距离最远，位于波场云图的前端；衍射横波的传播速度较慢，位于衍射纵波之后。从能量变化可以看出，衍射横波的能量要远远大于衍射纵波。另一部分瑞利波已沿着裂缝表面，绕过了裂缝底端，呈地滚式向上沿着裂缝右侧表面继续传播。此外，在轨道板内部的纵波和横波呈圆弧状继续按照原来的轨迹传播扩散，而沿着轨道板表面的瑞利波也呈地滚式继续向左侧传播。

图6 t=5×10-5s时模态转换产生衍射体波

如图7所示，当t=6.0×10-5s时，衍射纵波已传至裂缝右侧的轨道板表面。在轨道板表面可接收到衍射纵波的波形；同时，衍射横波仍然在轨道板内部继续传播。从图8中可以看出，衍射横波的传播速度与裂缝右表面瑞利波的速度相近。从能量变化可以看出，衍射出来的横波和纵波的能量随着传播时间的增加逐渐发生衰减，且相较而言，衍射纵波的衰减幅度较大。

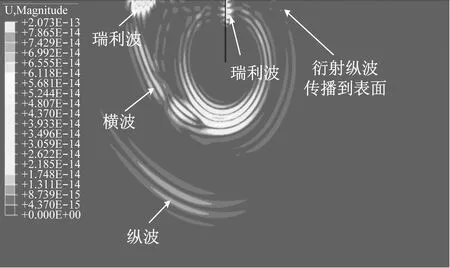
图7 t=6×10-5s时衍射纵波传播到表面

如图8所示，当t=8.0×10-5s时，衍射横波传至裂缝右侧的轨道板表面，经过裂缝后的瑞利波也到达轨道板表面。因此，在轨道板表面的接收点处可以同时接收到该部分瑞利波的波形及衍射横波的波形。

图8 t=8×10-5s时瑞利波传播到表面

由图5—图8，可以得出瑞利波的传播规律：在裂缝的左侧边缘施加激励时，激发出的瑞利波先向下沿着裂缝的左侧表面传播，之后绕过裂缝的底端，再向上沿着裂缝的右侧表面传播到轨道板上表面。由于这部分瑞利波的传播过程可反映出裂缝深度。因此，通过裂缝右侧轨道板表面接收到的瑞利波波形，就可获取瑞利波到达接收点的时间，结合传播路径对应的几何关系，便可计算出裂缝的深度[11-13]。

4 基于时差法的轨道板裂缝深度表征方法

将d分别设置为0.03 m、0.06 m、0.09 m、0.12 m，建立轨道板有限元模型，测得波形图如图9所示。

a)d=0.03 m

结合弹性波场云图可知：瑞利波在传播中先经过裂缝的左右两侧表面，再传播到轨道板的上表面。因此，瑞利波的传播时间最长。此外，由于瑞利波自身的能量较强，故可较为方便地找到波形图中瑞利波到达接收点时波形峰值对应的特征点。

由图9可知，随着轨道板表面裂缝深度的增加，特征点对应的时间也会随之增加。这说明裂缝深度对相应波形峰值的到达时间产生了较大影响，有一定的滞后效应。由此，可通过特征点的时间来计算裂缝深度。

以图2中模型为例，在裂缝左侧边缘施加激励源，则：

(4)

式中：

tR——瑞利波峰值到达接收点的时间；

t0——激励源的滞后时间。

基于瑞利波传播时间差法的原理，分别取各波形图中的tR，利用式(4)即可计算出d。由图4可知t0=1.4×10-5s；由轨道板材料介质参数计算可得vR=2 248 m/s；结合图5—图8波形图中tR，得到d值计算结果如表2所示。

表2 d值计算结果

由式(4)可得出d的理论曲线如图10所示，并将表2中的d的计算值标注在图10中。

图10 d的理论曲线及计算值

由表2及图10可见：d计算值与模型设置值较为接近；随着裂缝深度的不断增加，相对误差也越来越小。这说明该轨道板表面裂缝深度检测方法较准确，有一定的应用价值。与传统的检测方法相比较，该方法无需对轨道板结构造成损伤，即可实现对表面裂缝深度的检测，且检测方便、成本低、效率高，计算所得的d值相对误差较小。该方法还可应用于大体积结构的无损监测。

5 结语

针对目前轨道板裂缝检测方法存在的人力成本高、检测时间长且准确率较低等问题，本文提出了一种基于瑞利波的轨道板裂缝检测方法。通过建立含有表面裂缝的轨道板二维有限元模型，得到轨道板的波场云图。分析波场云图可知，瑞利波在遇到裂缝时会沿着裂缝表面呈地滚式传播。利用瑞利波的传播时间差，可实现对轨道板表面裂缝的深度检测。模拟计算结果显示，d的计算较为精确，相对误差能满足工程要求，且随着d的增加，相对误差也越来越小。