织物纹理基元自适应Gabor滤波器的疵点检测方法

李丑旦,祝双武,马阿辉

(西安工程大学 纺织科学与工程学院,陕西 西安 710048)

在织物面料的生产过程中,织物疵点的检测是其质量控制与检测的一项重要环节[1]。传统的织物疵点检测是由工人通过视觉检查进行的,存在劳动力成本高的问题[2],同时人工检测受工人工作时长、工作环境、熟练程度等多种主观因素影响,检测结果的可靠性存在争议[3]。20世纪70年代以来,随着数字图像技术的不断发展,机器视觉在工业上广泛应用,为织物疵点的自动检测提供了一种新的方法和研究方向[4-5],许多基于机器视觉的织物缺陷检测算法也相继被提出[6]。

织物缺陷检测算法可分为基于统计的方法[7]、基于频域分析的方法[8]、基于模型的方法[9]、基于学习的方法[10]、基于结构分析的方法[11]和多种方法混合与比较的方法。Gabor变换作为一种常用的频谱分析工具,能够在频域中通过不同方向、不同尺度提取相关的特征,在空间域和频率域中具有最佳联合定位的优点,因此也常用于织物纹理背景过滤[12]。目前,基于Gabor变换实现织物疵点检测的方法可分为两类[13]:基于Gabor滤波器组的检测方法[14]和基于优化Gabor滤波器的检测方法[15]。基于Gabor滤波器组进行织物疵点检测需要多个Gabor滤波器组合进行滤波处理,但滤波器组合数量的增加加大了算法的计算复杂度,大大降低了图像处理的效率,难以完成织物疵点实时监测检测任务,因此研究通过对滤波器优化的方法进行织物疵点检测。Gabor滤波器参数的选择对滤波效果有很大影响,合适的Gabor参数能够很好地将背景和疵点分离,去除背景纹理对疵点检测的干扰,从而实现对织物的快速检测。目前,针对寻找滤波器参数最优组合的算法有基于粒子群算法[16]、基于Gabor滤波器的自动检测算法[17]、基于遗传算法优化Gabor滤波器[18]等。针对Gabor滤波器在使用过程中,难以选取最优参数组合的问题,提出通过将织物的纹理基元结构与Gabor滤波核参数相互适应,通过分析Gabor滤波核与织物纹理结构之间的联系,找到Gabor滤波器最优参数组合,最后用寻找的最优滤波器对织物纹理进行滤波,实现了消除背景突出织物疵点的效果。

1 Gabor滤波器的特征及其数学描述

1.1 Gabor滤波器特征

傅里叶变换是一种用于信号处理的有力工具,在图像处理的过程中,通过对图像进行傅里叶变换,将图像从空间域转换到频率域,并在频域上提取到图像的频谱图、幅值信息等频域特征。但是由于傅里叶变换容易丢失时间和位置的局部信息,在应用过程中存在局限性。为了从傅里叶变换中提取到局部特征,1946年D.Gabor首次提出Gabor变换,通过对傅里叶变换引入了时间局部化的窗函数,得到了窗口傅里叶变换,又称为短时傅里叶变换或Gabor变换。

Gabor滤波器的波形与人类视觉系统中简单细胞的视觉皮层感受野响应非常相似,如图1所示,对Gabor滤波器波形图1(b)与脊椎动物视觉皮层感受野响应图1(a)进行对比并获取了两者的残差图1(c)。

从两者的残差图1(c)可见两者相差极小,基于Gabor滤波器的这一性质,在图像处理、模式识别及计算机视觉等领域中常用Gabor滤波器来实现人脸识别、图像的纹理特征提取、图像匹配等。研究发现,Gabor滤波器在图像处理中对于纹理特征的表达和分离以及提取目标的局部空间和频率域信息方面都有很好的表现。

图1 Gabor滤波器与脊椎动物视觉皮层感受野响应对比图

1.2 Gabor滤波器的数学描述

Gabor滤波器作为图像尺度表示和特征分析的常用工具,可以方便实现图像的尺度变化。二维Gabor滤波器表达式为:

式中:δx和δy分别为高斯核函数在x轴和y轴两方向的尺度参数;f0为正弦调谐函数的频率;θ为旋转角度;(x',y')经过旋转θ得到

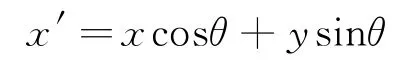
和

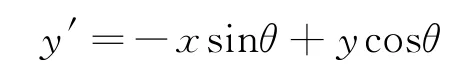
经过Gabor滤波后的图像R(x,y)表达式如式(2)所示。

式中:T(x,y)为待测织物图像;T(x,y)为经Gabor滤波器滤波后的特征图像;*为图像的滤波操作,表示Gabor滤波器对图像进行卷积处理。

在Gabor滤波器对图像进行卷积操作的过程中,Gabor特征主要依靠滤波核在频域对信号进行加窗,获取对图像局部信息的特征描述。一个Gabor核能获取到图像某个频域邻域的响应情况。在进行卷积操作时,滤波核大小对图像信息非常敏感,不同的核大小对图像纹理滤波效果有较大差异,因此适当的滤波核尺寸能充分发挥Gabor滤波器对纹理图像的滤波作用,以达到织物疵点检测的目的。

2 织物纹理基元

纹理是以像素的邻域灰度空间分布为特征,无法用像素点来定义。对于机器视觉来说,纹理是为了分割和识别场景或物体表面类型而产生的一种视觉标记。对纹理的研究就是对图像特征的研究,即图像的纹理分析,来达到分类和识别场景的效果。由于织物是由经纬纱线按照一定的组织规律交织而成,织物大多有着重复的纹理特征,为了更好地实现对织物疵点区域的识别与分割,需要获取织物纹理基元。采用自相关函数来进行织物纹理基元的测量。

对于具有重复性纹理的织物图像,其图像的自相关函数将会表现出固定的周期性,这个固定的周期等于相邻纹理基元之间的距离,应用自相关函数,能够计算出纹理图像的纹理周期和纹理基元的大小。

对于一幅N*N图像的自相关(Auto-correlation)函数p[k,l]定义为:

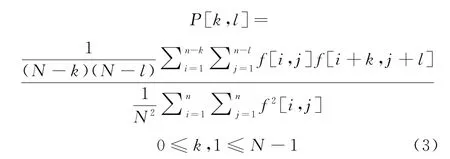
如图2(a)、(b)所示,是用自相关函数对织物图像生成垂直与水平方向的自相关曲线,从图2中可以看出自相关曲线具有明显的峰值、谷值和波形周期。通过图2(a)中曲线右侧峰值和图2(b)中曲线下侧峰值垂直与水平像素位置可以得出织物纹理基元信息为16*17。

图2 织物自相关曲线与基元标记

3 基于织物纹理基元分析的Gabor疵点检测方法

在织物疵点的视觉自动检测过程中,需要不断减弱织物的背景,即把织物正常的纹理区域信息弱化,同时突出疵点区域的信息,以便把织物的疵点检测出来。鉴于纹理织物图像有明显的周期性、方向性和均匀性等特征,根据织物图像的纹理特征提出一种基于织物纹理基元自适应Gabor滤波器的疵点检测方法。该检测方法首先通过对正常的织物进行纹理分析和特征提取,得到织物的纹理基元周期特征,再依据提取的纹理基元特征设计最优的Gabor滤波核参数,对正常纹理进行滤除,突出疵点区域信息,实现织物的疵点检测。

Gabor滤波器的带通特性要求在滤波器应用过程中根据处理图像的纹理特性确定Gabor的滤波核参数,采用适当的滤波核来对图像进行滤波处理。

Gabor滤波器对图像进行滤波处理时,通过Gabor滤波器的滤波核与图像进行卷积,图像卷积过程中核大小对纹理信息是非常敏感的,核的大小直接影响到最终的滤波效果。因此,在Gabor滤波器的使用过程中需要对Gabor核大小参数合理设计,得到纹理图像理想的Gabor滤波器,才能对纹理图像实现很好的滤波处理,达到疵点检测效果。

研究发现,Gabor滤波核与纹理基元有关,为了进一步确定滤波器核大小与纹理基元的关系,要先对采集的织物图像进行纹理基元试验。通过使用自相关函数计算得出图3(a)的纹理基元为9*9,分别设计7*7、9*9、11*11三个尺度的滤波核对图像进行滤波处理,得到效果如图3所示,同时表1列出了纹理基元与滤波核相互关系。分析可知:当滤波核与纹理基元相差较大时,对织物纹理的滤波作用较差。如图3(a-1)所示,可以看出当滤波核的尺寸小于织物纹理基元的大小时,对于正常纹理进行滤波操作并未获得很好的滤除效果,图像仍然存在部分纹理背景;当滤波核大小比纹理基元大时,滤波处理效果如图3(a-3)所示,滤波器在抹除正常纹理背景的同时也会将疵点区域抹去部分,使得滤波后图像的疵点面积不明显,较难分割出疵点区域,在检测过程中会造成漏检;当滤波核大小与纹理基元相同时,如图3(a-2)所示,能够很好地进行正常纹理背景消除并留下疵点区域。

图3 纹理基元与Gabor滤波核效果

表1 纹理基元与滤波核参数

通过对Gabor滤波核与纹理基元大小的试验研究发现,Gabor滤波核大小与织物的纹理基元的大小相近时,对于织物的正常纹理滤除效果最好,可以实现将正常纹理滤除,突出疵点区域的效果。

4 结果与分析

4.1 试验结果

为了进一步验证纹理基元与Gabor滤波核设计方法的有效性,用采集的织物样本对本文的算法进行评估。不同织物疵点检测效果如图4所示。

通过对常见的织物疵点断针如图4(a-1),粗节纱如图4(c-1,d-1)以及油污如图4(e-1)等进行试验,从图4可以看出,该检测方法能够实现较好的疵点检测效果,说明该方法具有一定的有效性。

图4 基于纹理基元的Gabor滤波器疵点检测效果

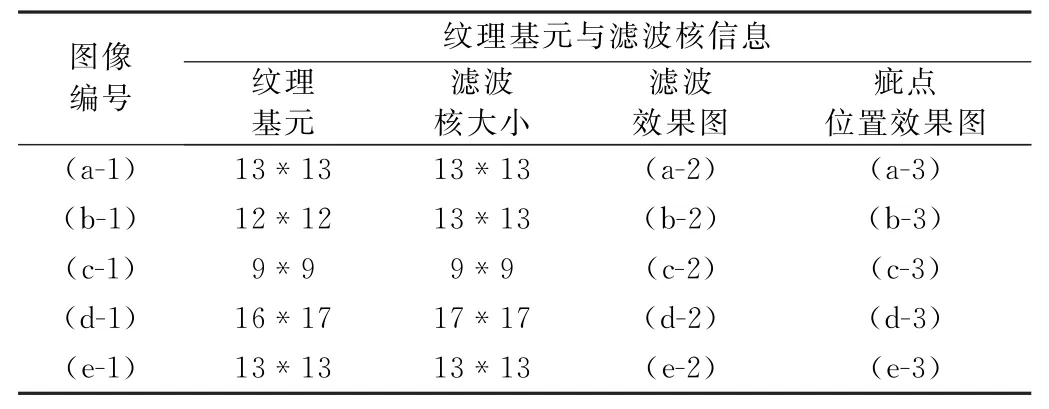
表2 纹理基元与滤波核参数

4.2 与其他算法检测效果对比

为了检验方法的稳定性和鲁棒性,选取TILDA标准织物图像库中尺寸为256×256像素的织物样本作为对照,将该疵点检测算法与文献[18]和文献[19]中基于Gabor滤波器组的疵点检测算法进行对比,通过二值特征图像对疵点检测的效果进行评估,检测结果如图5所示,试验结果证明,该方法是有效和实用的。

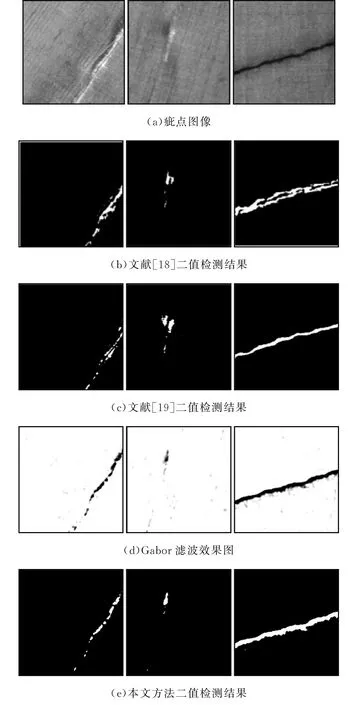
图5 疵点检测效果对比

由图5可看出,两种方法都可以检测出疵点的存在,但本文所提出的方法所检测出的疵点区域更加明显,疵点区域面积较为集中,疵点区域分割更为完整,在疵点判断过程中的准确性更高。

4.3 疵点检测正确率比较

为了检验方法的检测准确率,从TILDA标准织物图像中选取60幅作为检测样本,包含45幅疵点图像,15幅不含疵点的图像,其中,n为图像的边长,l为滤波器的边长,检测样本的检测结果见表3。

表3 疵点检测结果统计

从表3数据可得出,本文所采用的检测方法正确率高于文献[18]和文献[19]的正确率,由此可说明本文算法对于疵点检测具有更高的检测准确率和检测效率。

检测效果如图6所示。图6(a)为TILDA标准织物疵点图像,图6(b)为Gabor滤波效果图像,可以看出滤波器很好地将织物正常背景滤除,突出了疵点区域,图6(c)为滤波后的疵点二值分割图像,实现了较好的疵点分割。

图6 基于纹理基元的Gabor滤波器疵点检测效果

5 结 论

在对织物中漏针、粗节纱、油污等常见疵点进行研究后,提出基于织物纹理基元的自适应Gabor滤波器的疵点检测方法。主要实现了(1)通过分析织物纹理基元的特征,设计最优Gabor滤波器核大小;(2)应用自适应的Gabor滤波器对织物疵点图像进行滤波实现对织物疵点的自动检测;(3)通过与文献进行对比试验,证明了方法的有效性,实现了98.33%的检测准确率。对织物图像进行疵点检测试验发现,对于大部分织物图像通过设计合适滤波器均可检测出纹理发生突变的区域(即疵点区域),从而实现织物疵点的快速自动检测目标,这也证明了本文检测方法对于设计最优Gabor滤波器是有效的和实用的。