面向列的混合式数据筛选算法
2022-12-09郑月锋李文倩
郑月锋,李文倩
(吉林师范大学 数学与计算机学院,吉林 四平 136000)
采集来的数据存在冗余性[1-2]、不便于进行数据分析和对数据做进一步处理操作,因此需要对采集来的数据进行去重和去冗余等数据清洗操作[3].常用的数据清洗方法有众包方法[4]和ETL方法[5]等,这些方法主要是针对数据中的记录或者属性来清洗.本文提出的MRMCPSO算法是在不改变行数据的情况下,对列数据进行筛选,进而达到消除冗余数据的目的.由于没有对行数据进行筛选,因此,本算法适合数据记录不多,而适合属性数据众多的数据集.
1 MRMCPSO算法描述
1.1 MRMC过滤算法
本文提出的MRMCPSO算法是把过滤算法和包裹算法混合在一起,进而发挥两种算法的优势.在过滤算法中用肯德尔等级相关系数(Kendall Rank)[6]来衡量标签和特征之间的相关性,用欧式距离(Correlation Distance)[7]来衡量特征之间的冗余性.采用最大相关最大冗余算法(MRMR)[8]中相关性和冗余性等比率结合的策略,把两者结合起来形成最大秩系数最小距离(MRMC)算法.MRMC算法的伪代码见算法1.
算法1 MRMC算法伪代码
(1)输入参数:数据集,最终特征集合:LasetF={},变量i初值为0,dsF表示数据集,Fi表示被选中的第i个特征;
(2)输出:特征的排序;
(3)根据特征与标签之间的最大秩系数,从数据集dsF中选出一个特征存放在LasetF中(LasetF={Fi}i=1);
(4)数据集中减掉已经被选中的特征,dsF=dsF-{F1};
(5)根据特征与标签之间的最大秩系数和特征之间的最小距离,从数据集dsF中挑选出第二个特征(Fi,i=2)放在LasetF中(LasetF={F1,F2});
(6)数据集中减掉已经被选中的特征,dsF=dsF-{F2};
(7)当数据集dsF不为空时,进入循环;
(8)根据特征与标签之间的最大秩系数和特征与特征集之间的最小距离,从数据集dsF中挑选出第i(i>2)个特征(Fi)放在LasetF中(LasetF={Fk,k=1,2,…,i});
(9)dsF= dsF-{Fi};
(10)i=i+1;
(11)循环结束.
1.2 MRMCPSO算法
粒子群算法[9-12](PSO)是群智能优化算法中最典型的算法.它能够通过群体智能的特点在搜索空间中找到满足条件的最优解.通过模拟小球落地时的弹跳轨迹[13-15],把MRMC算法和PSO算法结合起来,形成MRMCPSO算法.模拟小球落地后弹起轨迹的公式为
y=|「6cosx+8sinx+5rand()⎤|.
(1)
其中:y表示弹起的离地距离,x表示时间,rand表示随机数,cos和sin分别表示余弦函数和正弦函数,“||”表示取绝对值,“「⎤”表示向上取整.x的范围是[1,100],y的值为1~15之间的正整数.
在MRMCPSO算法中,MRMC算法只执行1次,PSO算法执行的次数与迭代次数相同.在PSO算法中,种群的初始化采用随机化方法,数据集由MRMC算法执行后的前K个列组成,K的值由公式(2)确定:
(2)
其中:符号“⎣」”表示向下取整,Fnum表示数据集中列的数量,Rrownum表示数据集中行的数量,rand()是随机数在(0,1)的小数,randnumber是10倍的随机数并且取整,是1~10之间的正整数.MRMCPSO算法流程图见图1.
流程图中涉及一些参数,现解释如下.t表示迭代的次数,gbesttimes表示获得最大值的次数,best表示算法每次迭代获得的最优值,bestnest表示取得best值时挑选的列,i是Nochange数组的下标表示次数,Nochange数组存放公式(1)计算获得的前10个数据,gbest表示算法最终获得最优值,gbestnest表示取得gbest值时挑选的列.
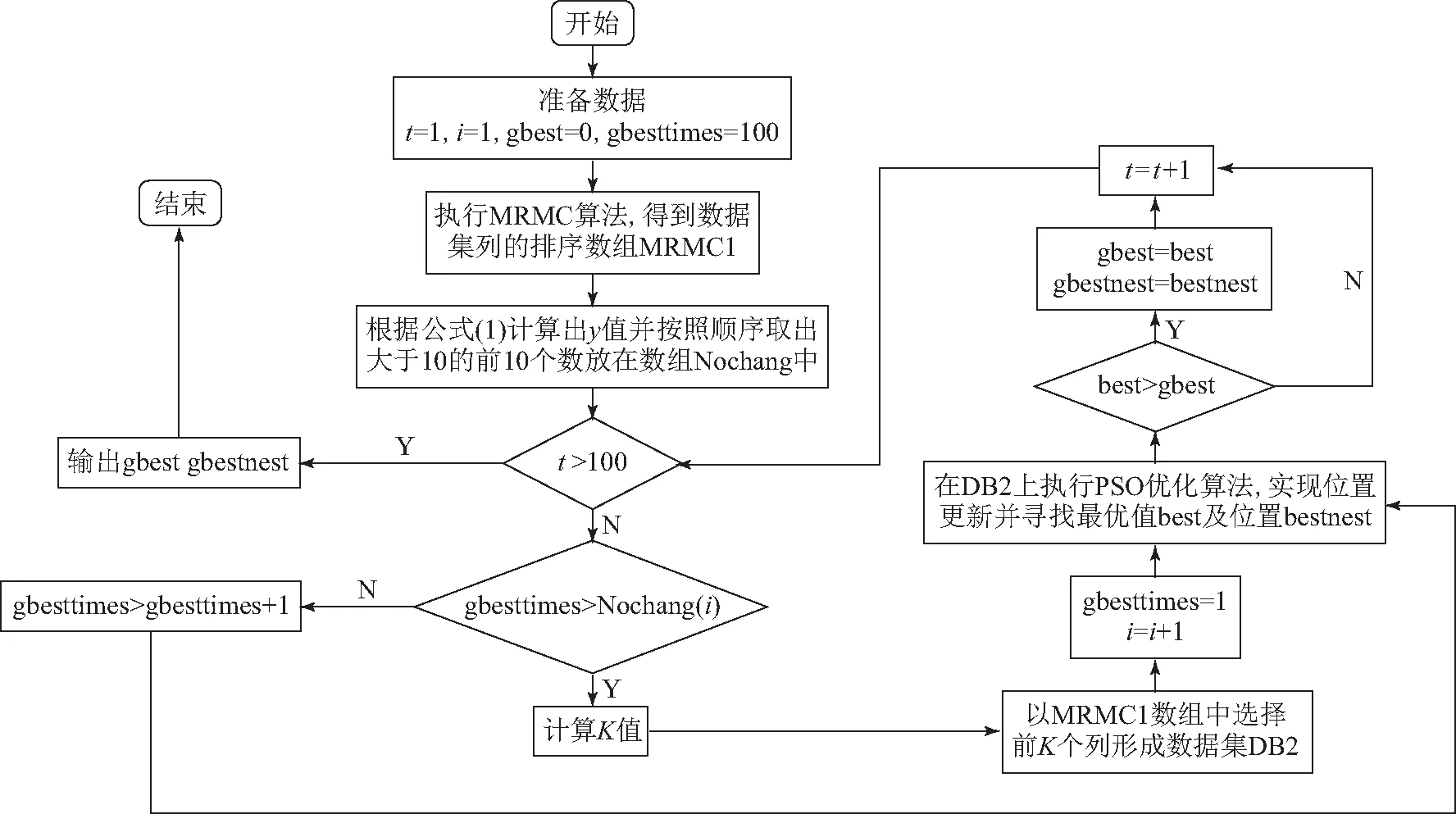
图1 MRMCPSO算法流程图
2 实验结果与分析
2.1 实验数据
本实验选择西安交通大学雷亚国[16]提供的轴承数据集并对下载后的数据集进行了处理.选择前2种工况下的所有原始数据集(10个),每个原始数据集根据行和列分成2个初始数据集(总计20个).每个初始数据集以数据量(行的数量)为基础,前取10%为合格数据并添加标签“1”,后取5%为损坏数据并添加标签“0”.初始数据集提取15%的数据量后形成的数据集作为实验使用的数据集.为扩大数据范围,对初始数据集获取的数量翻倍,10%改为20%,5%改为10%,标签添加方式不变,又形成20个数据集.实验用的40个数据集的信息见表1.
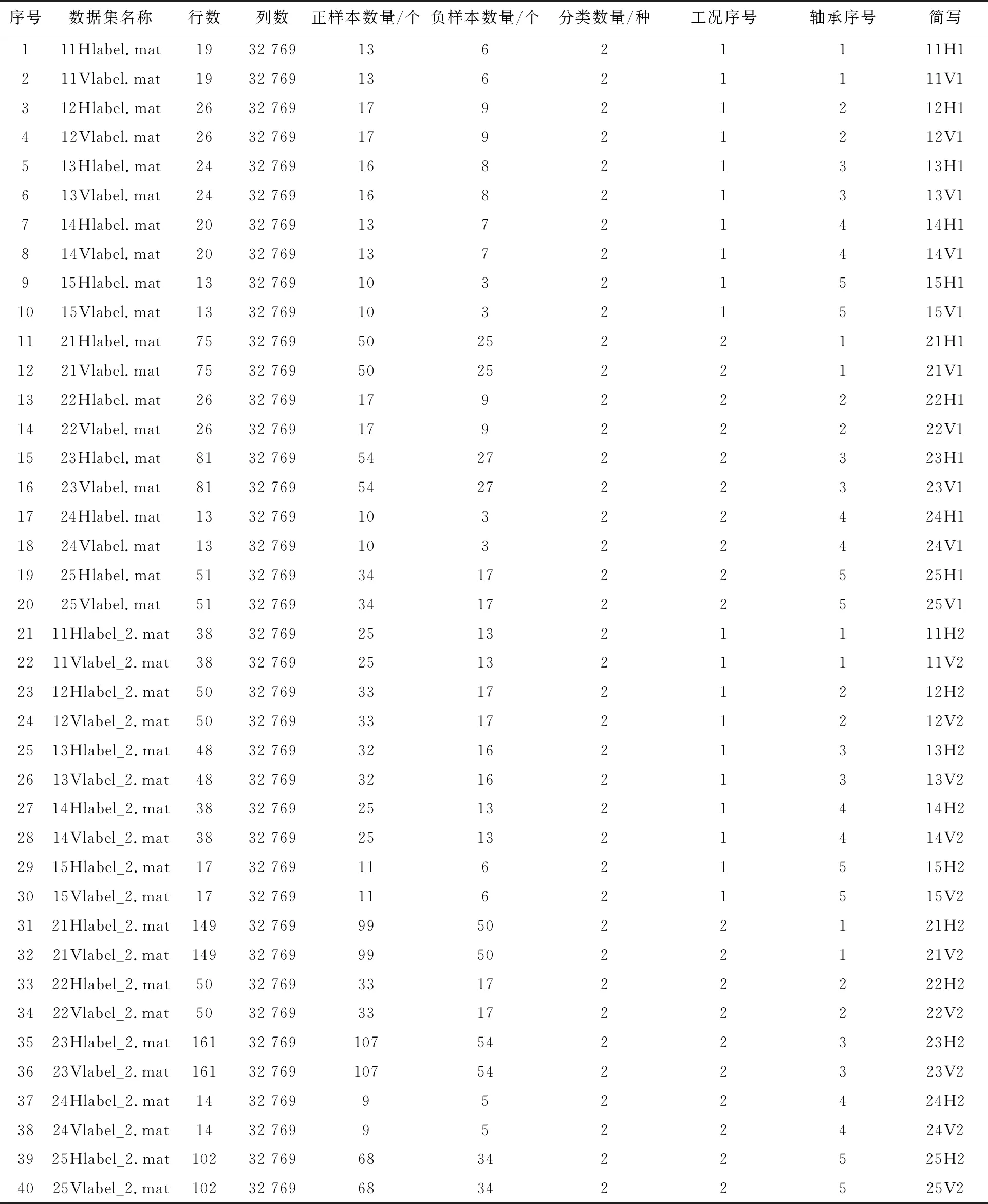
表1 实验用数据集信息
2.2 实验结果
分别用MRMR+PSO算法(最大相关最小相冗粒子群优化算法)、MRMR+GA算法(最大相关最小相冗遗传优化算法)、MRMR+BBA算法(最大相关最小相冗二进制蝙蝠优化算法)、MRMR+ GWO算法(最大相关最小相冗灰狼优化算法)与本文提出来的MRMCPSO算法进行比较.实验参数设置与文献[17]基本相同.
5种算法在每个数据集上运行10次.选择每个算法在每个数据集上的平均分类准确率和平均特征子集长度,形成表2.
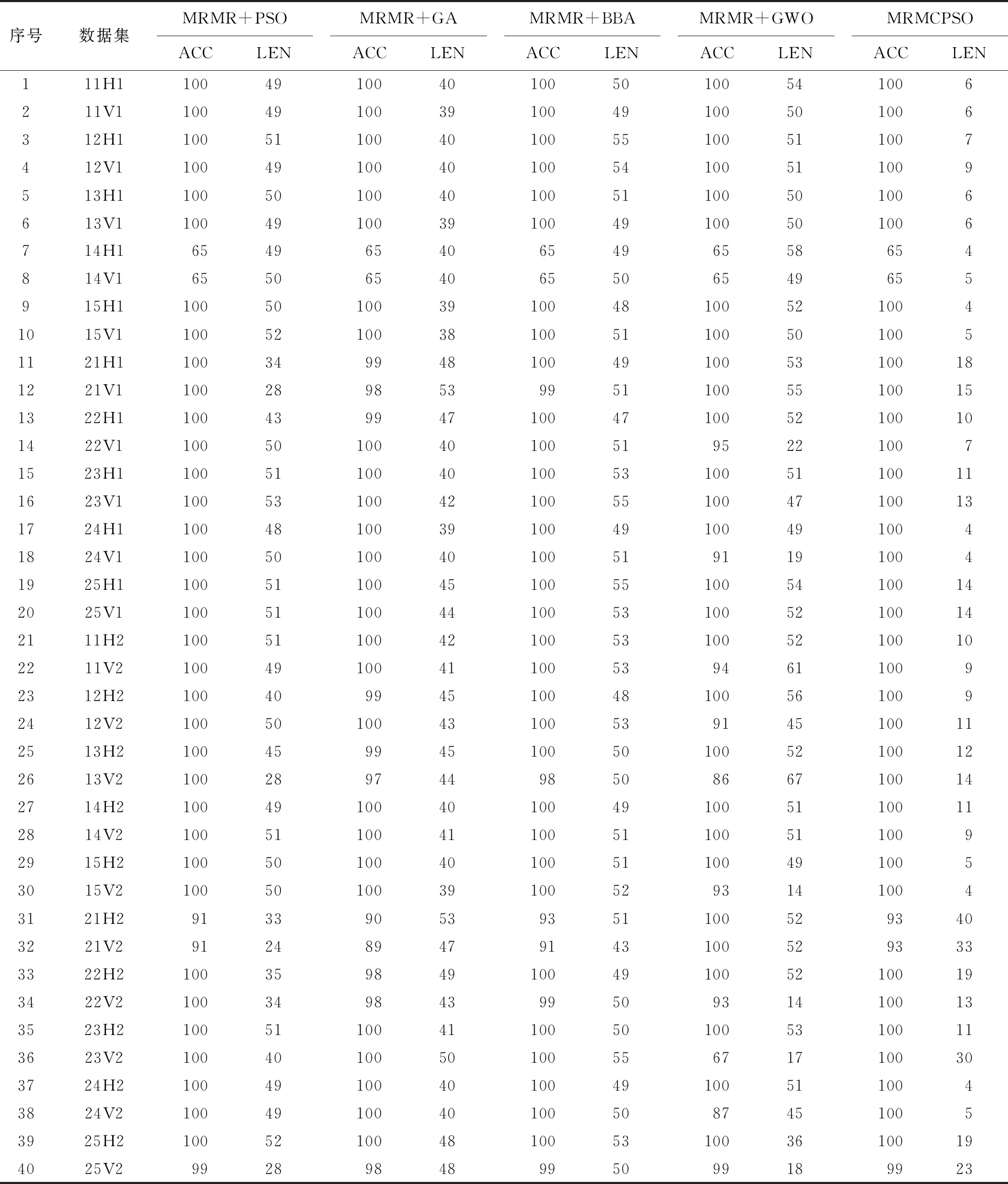
表2 5种算法在40个数据集上ACC平均值和LEN平均值
从表2中可以看出,5种算法对数据集中的列筛选出100列以内.但是,与其他4种算法相比,MRMCPSO算法的分类准确率在38个数据集上是最高的.在40个数据集中,有35个数据集的分类准确率达到了100%,有3个数据集的准确率达到了90%以上,只有2个数据集的分类准确率达到了65%.因此,与其他算法相比,所提出的算法能够获得较高的分类准确率,为进一步筛选数据列奠定基础.
图2显示了5种算法在40个数据集上筛选出来的列的长度.可以看出绿颜色曲线基本上在其他颜色曲线的下面,这说明MRMCPSO算法筛选出列的数量是最少的.而且从表2中可以看出,MRMCPSO算法获得列的数量是原数据集的列数量的6‰~12‰之间.从数值上看,MRMCPSO算法筛选出列的数量有28个数据集是一位数,其他4种没有筛选出列的长度为一位数的数据集.在绿色曲线上有3个点即不在最下面,也不在最上面,其对应的数据集编号分别是30、31、40.这3个点表明MRMRPSO算法筛选出列的数量不是最多的.从整体上看,与其他算法相比,所提出的算法在能够获得较高分类准确率的情况下,筛选出了长度较短的列.
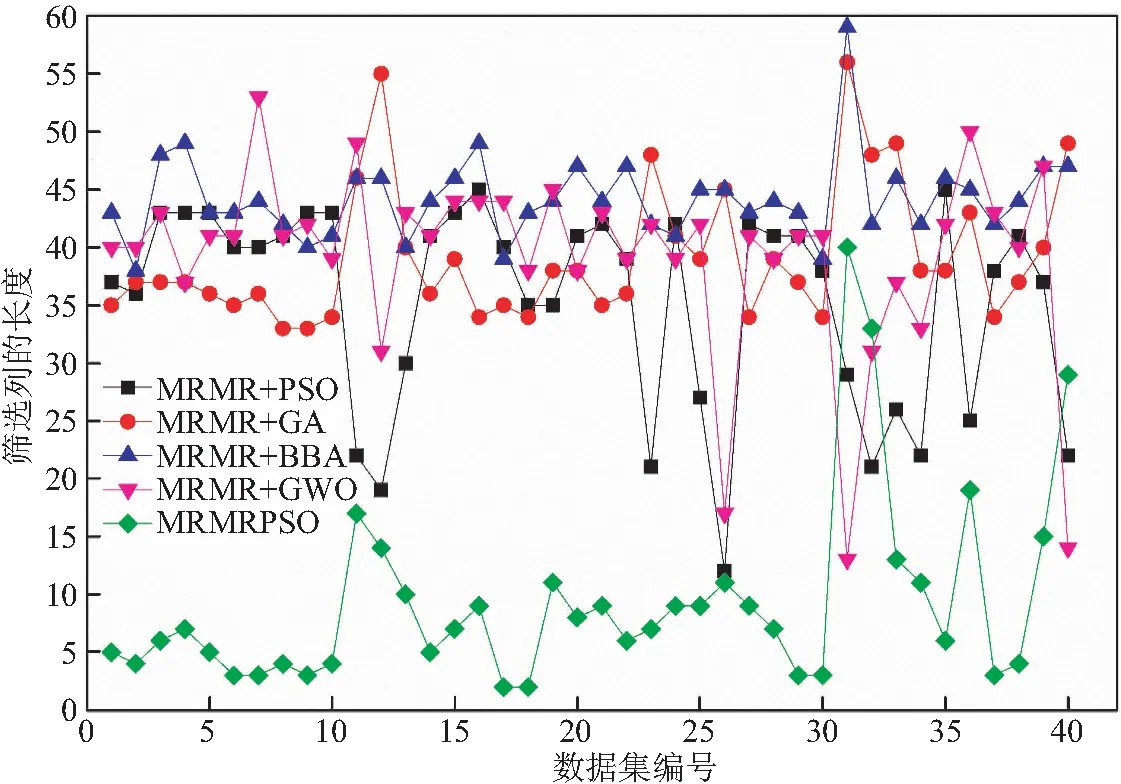
图2 5种算法在40个数据集上筛选列的长度
MRMRPSO算法与其他4种算法相比,从结构上采用了小球弹跳轨迹的思想,把MRMC算法和PSO算法混合起来,实现了对MRMC算法的多次调用,达到了突破局部最优的效果.MRMRPSO算法最终获得分类准确率较高,筛选出了长度较短的列,为数据的进一步处理奠定了基础.
3 结语
为消除采集数据中存在冗余数据,本文提出了MRMC算法,通过引入小球弹跳轨迹的思想,把MRMC算法和PSO算法混合起来,形成了MRMCPSO算法.通过在40个数据集上的实验结果表明,与其他4种算法相比,MRMCPSO算法在获得较高准确率的情况下,能够在实验数据集上筛选出长度较短的列,列的长度达到原来的6‰~12‰.
