直径相关锯齿-锯齿异质结碳纳米管的自旋极化
2022-12-09刘旭辉张海涵秦政坤
王 佳,刘旭辉,张海涵,秦政坤
(吉林师范大学 信息技术学院,吉林 四平 136000)
0 引言
碳基纳米材料的自旋极化行为由于其与磁性材料的设计和自旋电子器件的应用密切相关而被广泛研究[1-4].以往的研究发现锯齿边碳纳米管和锯齿边石墨烯存在自旋极化现象,并且根据锯齿边碳原子自旋方向的相同或相反呈铁磁或反铁磁耦合[5-8].石墨烯纳米带的研究表明,至少3个连续的锯齿边碳原子才会产生自旋极化现象[9].石墨烯纳米片和手性碳纳米管的研究发现扶椅边会抑制碳纳米材料的自旋极化[10-11],并且空位和掺杂等缺陷也可以抑制碳纳米材料的自旋极化[9,12].此外,与对称的几何结构和电子性质相比,非对称结构的自旋极化效应在生物医学药物传输[13]、定向输运和磁开关[14-15]等领域都引起了广泛的关注.然而,少数碳纳米管本身就是不对称的,因此构建新的不对称结构实现自旋调节是有必要的.
近几年,异质结构在各个领域都备受欢迎,如TiO2-x/g-C3N4纳米片[16]、WS2-MoS2-纳米带[17]和g-C3N4/LaMnO3异质结[18]等.当然,异质结碳纳米管由于结构的独特性也被关注[19-21].异质结碳纳米管的力学性质如杨氏模量和剪切模量已经被研究[22-23],结果显示锯齿-锯齿连接的异质结碳纳米管有最高弹性模量和最低的剪切模量;扶椅-锯齿连接的异质结碳纳米管的弹性刚度最低,但剪切模量最高[24];Stone-Wales缺陷能降低异质结碳纳米管的弹性和扭转强度[25].进一步,在“扶椅”和“锯齿”碳纳米管之间的异质结中,电荷从扶椅部分转移到锯齿部分[26].此外,先前的研究发现异质结碳纳米管两端之间的手性和角度,分子内连接长度和平均温度对热整流有影响且拉伸应力可以增加整流[27].对异质结碳纳米管热传导的理论研究发现热导率随缺陷数的增加而降低[28].对于单空位和硼掺杂的异质结碳纳米管研究显示形成能取决于异质结碳纳米管的手性且与尺寸无关[29].但异质结碳纳米管的磁性以及异质结碳纳米管两端的手性对磁性的影响尚未研究.
本文使用密度泛函方法[30-31]对氢钝化的有限锯齿-锯齿连接的异质结碳纳米管的自旋极化进行了深入的研究.与先前报道的同质锯齿边碳纳米管和石墨烯不同[7-8],异质结碳纳米管由于两端直径的不同导致锯齿-锯齿异质结碳纳米管的基态可能是反铁磁耦合双重态,也可能是铁磁耦合的高自旋多重态.本文的研究结果表明自旋极化行为可以通过异质结碳纳米管的直径来控制,这个研究可以为不对称分子器件的设计提供帮助.
1 模型和理论部分
1.1 模型
异质结碳纳米管通过在完美的六边形石墨晶格中引入一对Stone-Wales缺陷连接两个不同半径的碳纳米管[32].目前,异质结碳纳米管有三种连接形式,分别是扶椅-扶椅,锯齿-锯齿和锯齿-扶椅连接[24].本文专注于异质结碳纳米管的自旋极化效应,主要对锯齿-锯齿异质结碳纳米管如(6,0)-(5,0)、(8,0)-(5,0)、(10,0)-(5,0)、(7,0)-(6,0)、(9,0)-(6,0)、(8,0)-(7,0)、(10,0)-(7,0)和(10,0)-(9,0)进行研究.
1.2 理论计算
本文所有计算都使用了交换杂化密度泛函Heyd,Scuseria and Ernzerhof (HSE06)[33-34].因为使用HSE06泛函计算的带隙与实验数据非常吻合,比其他泛函得到平均误差小,因此HSE06泛函更适合电子局域系统.此外,HCNTs的自旋密度被HSE06、局部自旋密度近似 (LSDA)和Perdew、Burke和Ernzerhof (PBE)的半局部梯度校正函数计算.结果表明,使用HSE06计算的最大密立根自旋密度值比使用LSDA和PBE计算的更合理,这与先前的报道一致[10].所有的计算都使用6-31G (d,p)基组[35]完成.此外,±1e或±2e的带电结构的异质结碳纳米管也在相同水平下被计算.所有中性和带电结构都经过充分优化,以确认它们是局域最小值.并且在所有计算中都没有使用对称限制.对于优化的收敛阈值,最大力被设置为4.5×10-4Ha/Bohr,RMS力被设置为3×10-4Ha/Bohr,最大位移被设置为1.8×10-3Ha/Bohr,以及RMS位移被设置为1.2×10-3Ha/Bohr.对于SCF迭代,密度收敛到10-8.
2 结果与讨论
2.1 自旋密度分析
锯齿-锯齿异质结碳纳米管根据两端碳原子数目的不同有奇数和偶数电子之分.选择奇数电子的结构,如(6,0)-(5,0)、(8,0)-(5,0)、(10,0)-(5,0)、(7,0)-(6,0)、(9,0)-(6,0)、(8,0)-(7,0)、(10,0)-(7,0)和(10,0)-(9,0)异质结碳纳米管.其中(6,0)-(5,0)、(8,0)-(5,0)、(9,0)-(6,0)、(8,0)-(7,0)和(10,0)-(7,0)异质结碳纳米管的基态是二重态,(10,0)-(5,0)异质结碳纳米管的基态是四重态.而(7,0)-(6,0)和(10,0)-(9,0)异质结碳纳米管的基态是六重态.
基于优化的电子结构对自旋密度进行分析,如图1所示.对于(6,0)-(5,0)和(10,0)-(5,0)异质结碳纳米管,在半径较大一端管口的自旋方向向上且自旋密度最大,然后沿着管轴逐渐减小,最后趋近于0.对于(8,0)-(5,0)、(9,0)-(6,0)、(8,0)-(7,0)和(10,0)-(7,0)异质结碳纳米管,半径较大那端管口的自旋方向向上,另一端管口自旋方向向下,且两端管口的自旋密度最大,从锯齿边到管中心自旋密度逐渐减小.因此基态的特征在于局域在这些异质结碳纳米管的两边缘处碳原子的自旋方向相反,它们通过自旋的反铁磁耦合排列,类似于均质的锯齿边碳纳米管和石墨烯[10-11].而(7,0)-(6,0)和(10,0)-(9,0)异质结碳纳米管在连接处几乎没有自旋,它们的自旋密度也是在异质结碳纳米管两端口处最大,但是两端局部电子态的自旋方向相同.换句话说,(7,0)-(6,0)和(10,0)-(9,0)异质结碳纳米管的基态是呈自旋铁磁耦合,这与之前报道的均质锯齿边碳纳米管的基态耦合不同,但与均质锯齿边碳纳米管的高自旋态相似[8].然而,它们的二重态也是自旋反铁磁耦合.自旋极化分析结果表明不同异质结碳纳米管的磁耦合不同,因此可以通过调节异质结碳纳米管两端碳原子数目来调控自旋极化现象.

蓝色区域表示自旋向上,红色区域表示自旋向下
2.2 分子轨道分析
为了研究自旋极化的来源,分析了异质结碳纳米管的前线分子轨道(MOs).由于(6,0)和(9,0)碳纳米管是典型的碳纳米管,因此主要以(9,0)-(6,0)异质结碳纳米管为例进行分析,如图2所示.可以看出alpha电子的最高占据分子轨道-2(HOMO-2α)和HOMO-3α主要占据在(9,0)碳纳米管的管口.Beta电子的HOMO-2(HOMO-2β)主要占据在(6,0)碳纳米管的管口.而其他分子轨道都离域在(9,0)-(6,0)异质结碳纳米管上.所以对于自旋向上的自旋密度主要是由HOMO-2α和HOMO-3α贡献的,而自旋向下的自旋密度主要是由HOMO-2β贡献的.因此(9,0)-(6,0)异质结碳纳米管的自旋密度主要是由占据在纳米管两端的轨道贡献的,这与锯齿和手性碳纳米管相类似[11].此外,也分析了(6,0)-(5,0)、(8,0)-(5,0)、(8,0)-(7,0)和(10,0)-(7,0)异质结碳纳米管的分子轨道.相似的,这些结构的自旋密度也主要由局域在异质结碳纳米管两端管口的分子轨道贡献.
2.3 电荷对自旋密度的影响
以(9,0)-(6,0)异质结碳纳米管为例研究了电荷诱导的效应.图3是(9,0)-(6,0)异质结碳纳米管中性结构和±1和±2带电荷结构的自旋密度分布曲线.与中性结构(0e)相比,-1e,+1e和+2e带电结构的自旋密度在整个异质结碳纳米管上减小,且在连接处减小的最多.对于-1e结构,自旋密度在半径较大一端减小的较多.而对于+1e和+2e带电结构,自旋密度则在半径较小一端减小的较多.-2e结构的自旋密度分布相对复杂,它在(6,0)和(9,0)端减小,但在七边形缺陷处有轻微的增加.总之,增加或减小电荷对(9,0)-(6,0)异质结碳纳米管反铁磁耦合态的自旋密度影响较小.
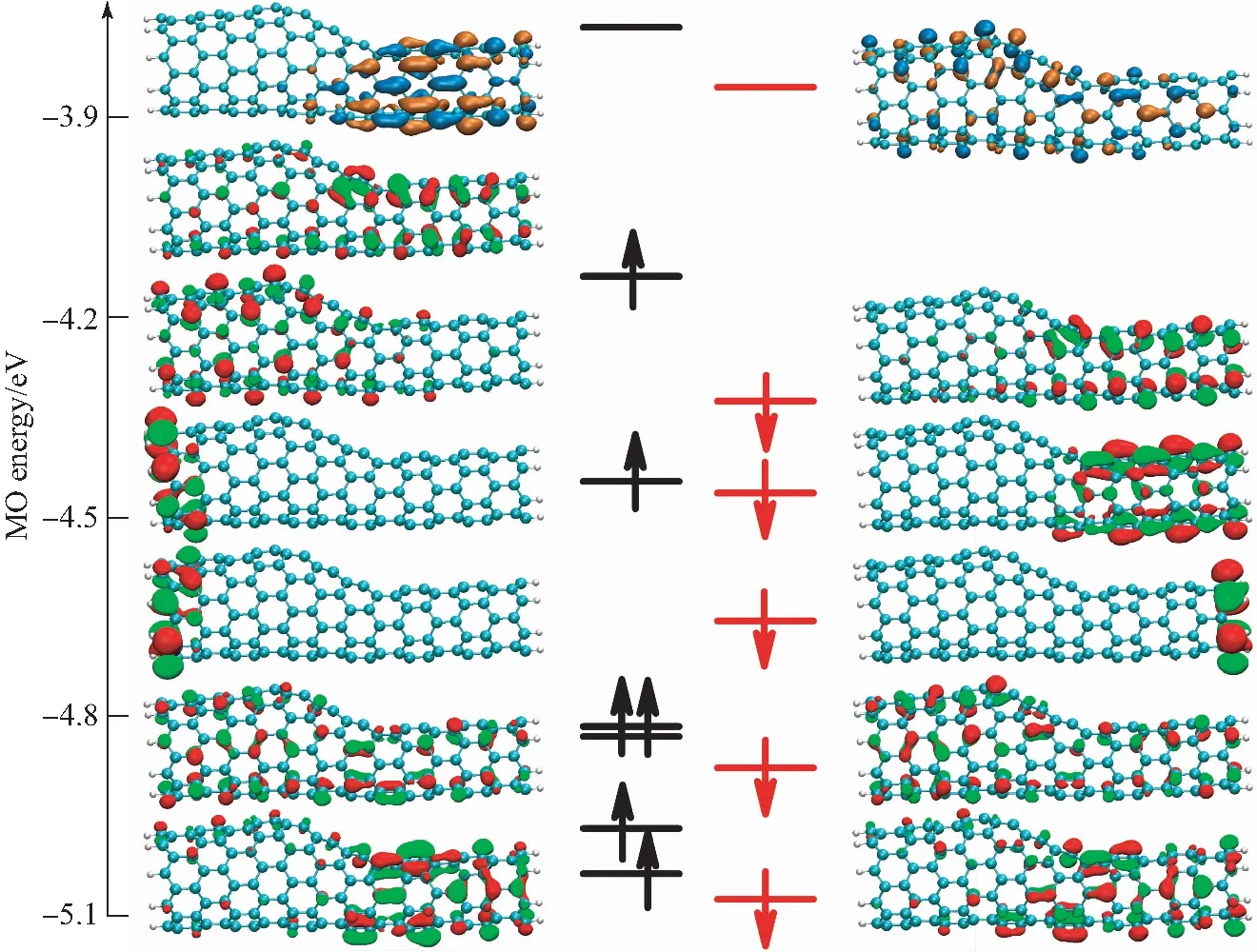
黑线和红线分别表示α-MOs和β-MOs,绿色和红色表示占据MOs,橙色和蓝色表示非占据MOs

黑线是中性结构的自旋密度分布曲线,红色、粉色、黑色、蓝色和绿色线分别代表-2e,-1e,0e,+1e和+2e带电结构的自旋密度分布曲线
3 结论
本文基于第一性原理研究了锯齿-锯齿异质结碳纳米管的电子结构.计算结果表明异质结碳纳米管的基态可能是自旋反铁磁耦合双重态,也可能是自旋铁磁耦合的高自旋多重态.分子轨道分析显示具有反铁磁耦合基态的自旋密度主要由占据在异质结碳纳米管两端的前线分子轨道贡献.进一步,(9,0)-(6,0)异质结碳纳米管的带电结构也被研究.结果表明,增加或减小电荷对反铁磁耦合态的自旋密度几乎没有影响.另外,可以通过调节锯齿-锯齿异质结碳纳米管的直径来实现自旋极化的调控,进而控制结构的磁性.因此,本工作为定向传输和自旋电子器件的设计提供了新思路.
