基于调度信号的自抗扰控制器设计研究

王佑，孙立明，薛亚丽

（1.清华大学能源与动力工程系电力系统国家重点实验室，北京 100084；2.明阳智慧能源集团股份有限公司，广东中山 528437；3.匙慧（北京）科技有限公司，北京 102308）

0 引言

能源系统低碳转型是我国实现碳达峰、碳中和目标的关键［1-2］，煤电机组在未来可再生能源占比大幅提高的背景下，将在保障电力安全和灵活调峰方面发挥重要作用。除了对燃煤发电机组进行灵活性改造外，提高现役燃煤发电机组在更宽负荷范围内快速变负荷运行能力也具有重要意义［3-5］。但燃煤发电机组具有结构和流程复杂、未知扰动频繁、运行工况特性变化大、多回路紧密耦合、大时滞大惯性等特点［6-7］，制约了机组的变负荷率，也对控制系统的设计和运行提出很大挑战。

自抗扰控制器（Active Disturbance Rejection Control，ADRC）是将经典比例-积分-微分（PID）控制与现代控制理论相结合的一种先进控制方法［8］。最早提出的ADRC是非线性控制器，由跟踪微分器、非线性组合和扩张状态观测器3部分组成。但是非线性ADRC 结构及控制器参数整定较为复杂，因此目前应用较为普遍的是线性ADRC［9］。相比于其他先进控制算法，线性ADRC 不依赖被控对象的精确模型，具有结构简单、整定方便、抗扰性能好和鲁棒性强的优点，近年来在热力过程控制领域得到应用和发展［10-13］。

线性ADRC 应用于大型燃煤机组控制时，主要面临2 个方面的问题，一是对于惯性和滞后较大的被控过程，扩张状态观测器（Extended State Observer，ESO）的观测效果不理想，导致ADRC 的控制效果欠佳，二是工况大范围频繁变化时被控过程非线性强，按照某一工况设计的ADRC 在其他工况控制性能有所降低。尽管采用设定值各阶导数的线性组合作为ADRC 的前馈控制量［14］，能够提高设定值快速变化时的跟踪能力，而利用模型信息对ADRC 改进控制结构进行参数整定，能改善其对大惯性过程的控制效果［15］，但当被控过程的惯性较大且动态特性随工况有明显变化时，上述方法的控制效果仍有改善空间。

为此，本文研究一种基于调度信号的前馈补偿自抗扰控制器及其设计方法，旨在解决大惯性被控过程在大范围频繁变工况运行时控制品质不佳的问题。通过引入调度信号，并利用被控过程在变工况下的动态模型信息，设计变参数的前馈补偿自抗扰控制器，分别使得前馈控制器、反馈控制器、补偿模块和扩张状态观测器随工况变化进行参数调整，从而提高自抗扰控制器对大惯性和变工况的适应能力。仿真对比试验验证了本文所提方法的有效性。

1 自抗扰控制设计原理

考虑如下的大惯性被控过程

式中：b0为系统增益b的估计值；f(t)为总和扰动。

则设计ESO：

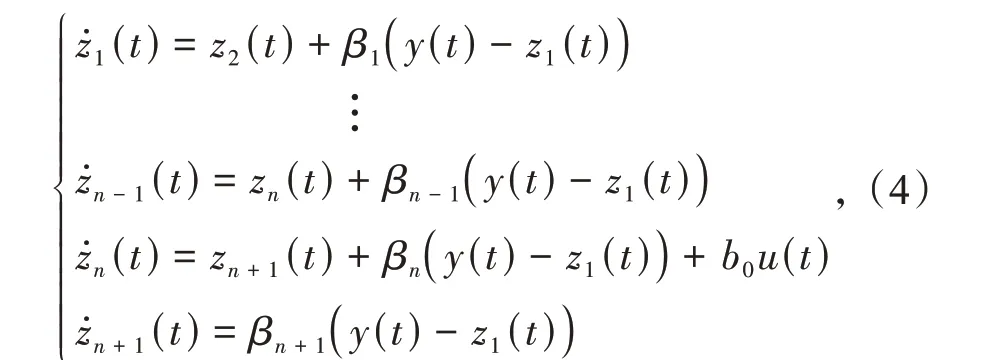
式 中：z1(t)，z2(t)，…，zn+1(t) 为ESO 的 输 出；β1，β2，…，βn+1为ESO的增益参数。

当ESO 的增益参数选取合适时，其输出z1(t)，z2(t)，…，zn(t)能够以较高的精度跟踪系统输出y(t)及其各阶导数y'(t)，…，y(n)(t)，zn+1(t)则能较好地估计系统的总和扰动f(t)。

此时设计线性控制器

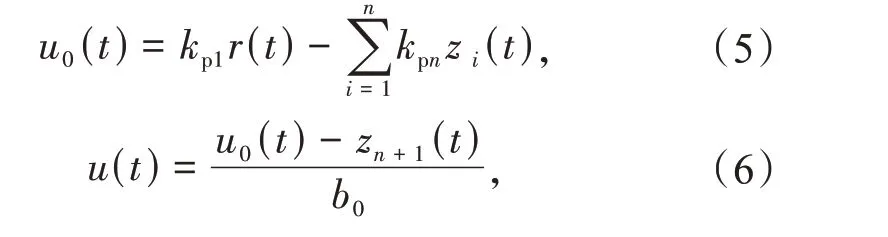
式中：r（t）为设定值；u0（t）为线性控制器输出；kp1，kp2，…，kpn为控制器增益参数。

由式（3），（5）和（6）可得

即经过ESO 的观测和扰动补偿，线性控制器的等效被控过程为n阶积分串联型，可以通过线性控制器进行控制。自抗扰控制系统的结构如图1所示。

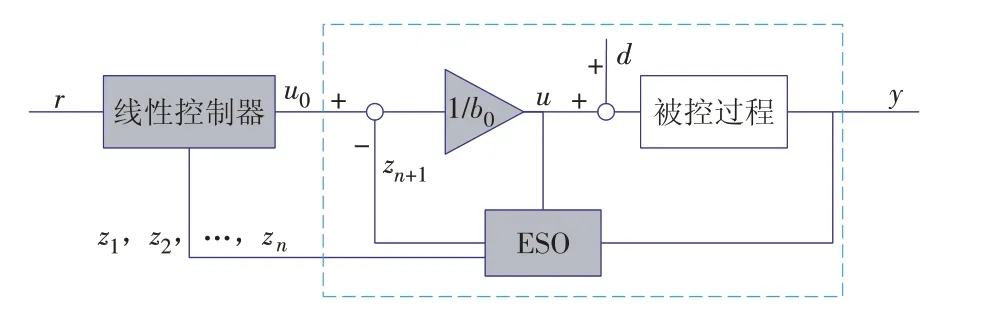
图1 自抗扰控制系统结构Fig.1 Control system structure of an ADRC

对于大惯性被控过程，为提高ESO 的观测效果，文献［15-16］借鉴文献［17］对纯时滞对象的改进设计结构，设计了惯性补偿环节，如图2 所示。文献［18］基于该设计结构提出了简便通用的定量化参数整定方法。以上方法已经在实际火电机组控制中应用，获得了控制效果的改进。

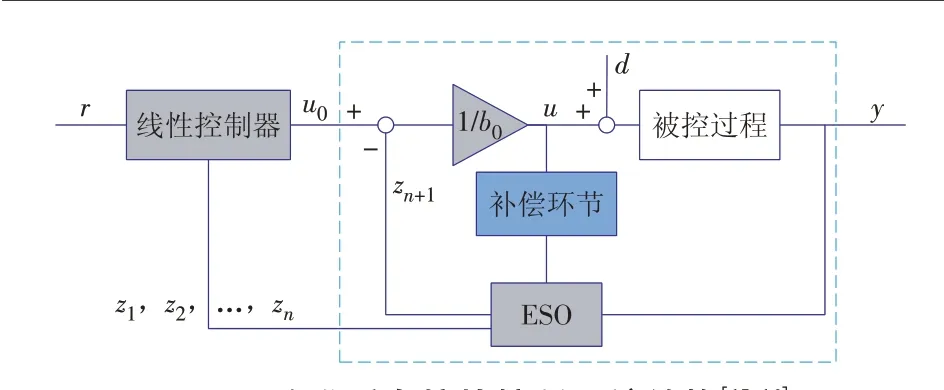
图2 改进后自抗扰控制系统结构［15-16］Fig.2 System structure of the modified ADRC［15-16］

2 基于调度信号的自抗扰控制器设计

上述ADRC改进设计方法提高了对高阶大惯性过程的控制效果，且通过观测补偿机制，能够一定程度上处理系统的非线性。但当被控过程在更大范围内变负荷运行从而具有强非线性时，控制效果仍有改进的空间。

为了克服火电机组频繁大范围变工况运行时被控过程非线性特性的影响，本文引入调度信号并利用被控过程在变工况下的动态模型信息，设计了前馈补偿自抗扰控制器，即在ADRC 改进设计的基础上，增加了前馈控制器，并令前馈控制器、反馈控制器、补偿模块和扩张状态观测器的参数随工况实时调整，从而提高自抗扰控制器对大惯性和变工况的适应能力。

控制系统结构如图3 所示。其中：r(t)为设定值；u(t)为控制量；y(t)为被控量；Q(t)为调度信号；uff(t)为前馈控制量；ufb(t)为线性反馈控制量；uTF(t)为控制量u(t)经过补偿环节后的输出；z1(t)～zm+1(t)为扩张状态观测器的输出；其中m为反馈控制器的阶次。

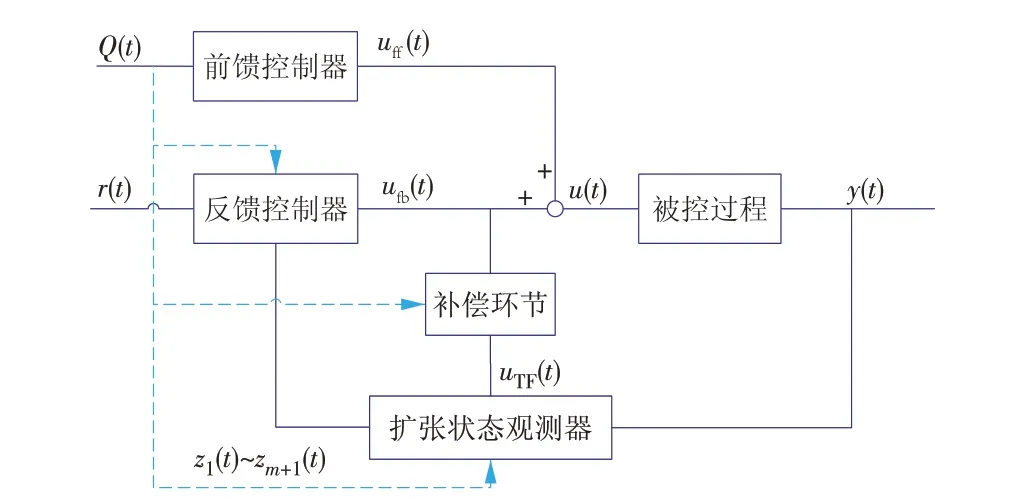
图3 基于调度信号的前馈补偿自抗扰控制系统结构Fig.3 Control system structure of the feedforward compensated ADRC based on scheduling signal

2.1 变工况模型信息

对于强非线性被控过程，通常用非线性度衡量系统的非线性特性。根据被控过程的非线性度，可将其变工况范围划分为q-1 段，得到q个工况点，每个工况点上的动态特性用线性模型来近似描述。设被控过程为自平衡过程，其传递函数为

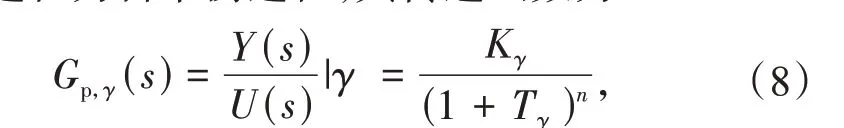
式中：γ为工况点编号，γ= 1，2，…，q；Gp，γ(s)为工况点γ对应的被控过程传递函数；Y（s）和U（s）分别为y（t）和u（t）的拉氏变换；Kγ和Tγ为工况点γ下模型的系统增益和时间常数；n为被控过程传递函数的阶次。

火电机组的强非线性通常是由于工况变化引起的，因此需选取能够代表被控过程工况变化特征和趋势的参数作为实时调度信号，且该信号与控制量之间的先验函数关系能够通过试验或分析预先获得。设Q（t）为实时调度信号，被控过程动态特性随调度信号而变化，则可根据变工况模型信息近似估计Q（t）对应的传递函数，从而用于控制器的设计

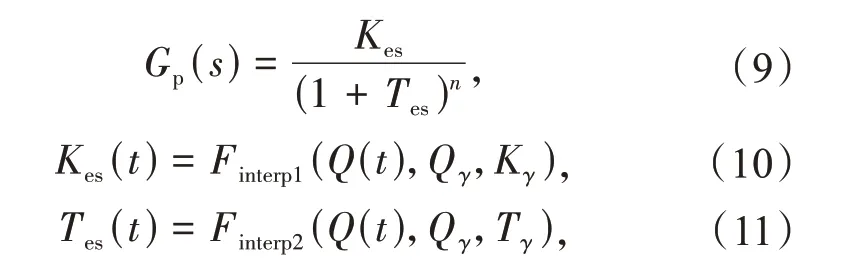
式中：Gp（s）为基于实时调度信号估计的被控过程传递函数；Kes和Tes为相应的增益和时间常数；Qγ为工况点γ对应的调度变量值；Finterp1和Finterp2为线性或非线性插值函数。

2.2 前馈控制器

当调度信号改变从而被控过程的预期工况发生变化时，通过设计前馈控制器，可以使控制量根据调度信号的预期变化而迅速变化，加快控制系统的响应过程。

若通过建模或试验获得两者之间的关系为

式中：uγ(t)为基准前馈控制量；Fff为调度变量与基准前馈控制量之间的非线性函数。

则前馈函数量uff(t)可基于上述关系和Q(t)插值获得，即

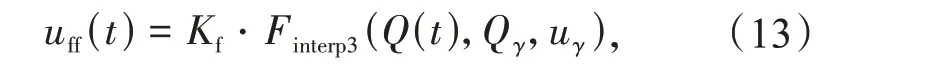
式中：Kf为前馈权重系数；Finterp3为相应的插值函数。

2.3 补偿环节

在变工况设计中，图3 补偿环节的设计原理是在系统工况发生变化时，产生一个与被控过程动态特性相匹配的动态补偿作用送入扩张状态观测器，减小状态观测误差，提高控制器对大惯性过程的控制效果。

补偿环节的传递函数设计为：

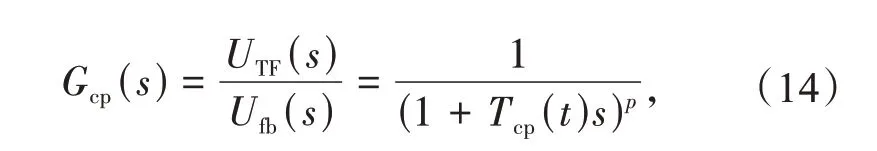
式中：Gcp(s)为补偿环节的传递函数；UTF(s)和Ufb(s)分别为uTF(t)和ufb(t)的拉普拉斯变换；Tcp为随调度信号变化的时间常数；p为补偿环节传递函数的阶次。

现代多自由度并联式力控末端执行器属于多输入多输出系统。它由多个支链组成，支链间存在耦合，且每个支链至少有1个恒力补偿作动部件，工具头的最终输出力和姿态由各支链及其恒力补偿作动部件决定。因此，应对它进行解耦控制技术研究，减小或消除各支链间的相互干扰，提高力控末端执行器的动静态性能及其可靠性。

补偿环节的设计应与被控过程动态特性随工况的变化规律相匹配，从而降低扩张状态观测器的等效被观测对象阶次，提高状态观测效果。本文中基于所获取的变工况动态模型信息设计补偿环节。其中：补偿环节的时间常数Tcp随调度信号实时变化以适应被控对象的动态，其实时值根据变工况模型信息和实时调度信号确定，即

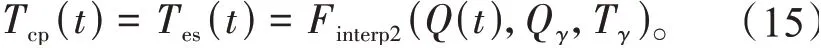
补偿环节的阶次p的选择取决于所采用的自抗扰控制器的阶次。若被控过程的阶次为n，自抗扰控制器的阶次为m，扩张状态观测器的阶次为m+1，则应有p=n-m，从而使得系统状态能够全部被扩张状态观测器所观测。

2.4 扩张状态观测器

在本文中，m阶扩张状态观测器的时域形式如下

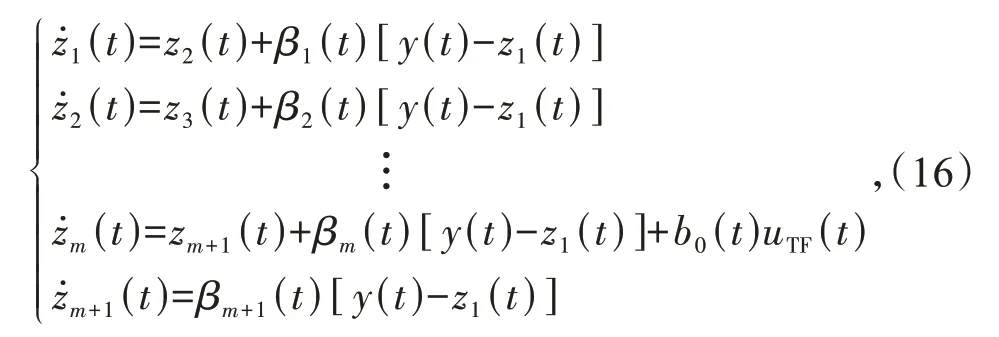
式中：zi(t)(i= 1，2，…，m+ 1)为扩张状态观测器的输出；βi(t)(i= 1，2，…，m+ 1)为扩张状态观测器的可调参数；b0(t)为反馈控制器的可调参数，均随调度信号变化。

参照文献［9］的参数定量化整定方法，扩张状态观测器的可调参数计算如下

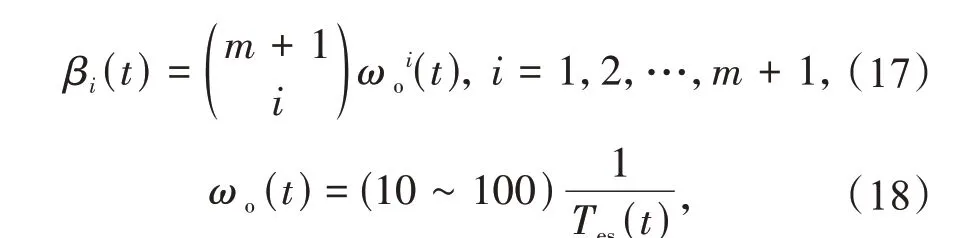
式中：ωo为扩张状态观测器的带宽。

2.5 反馈控制器

在工况变化或扰动发生时，反馈控制器能够根据设定值和扩张状态观测器的输出，对控制量进行调整，抵消观测到的总扰动并最终消除控制偏差。反馈控制量计算如下

3 仿真算例

以下通过仿真算例比较本文设计方法的可行性和有效性。设某燃煤机组以给煤量为控制量、以主蒸汽压力为被控量的传递函数为

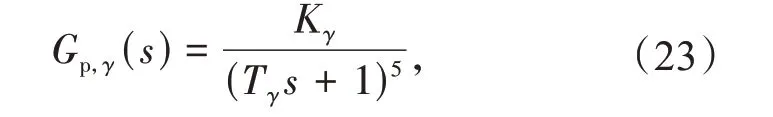
式 中：Kγ=［0.135 7，0.135 7，0.113 0，0.098 2，0.086 4］；Tγ=［400，300，250，220，200］；对应的负荷指令为Qγ=［0，99，165，250，330］；对应的给煤量基准值为uγ=［70，70，115，168，220］；对应的主蒸汽压力设定值为［0，9.5，13.9，16.5，19.0］。

以负荷指令为调度信号，并根据不同负荷点下的变工况模型信息、基准控制量和设定值进行控制器设计。

3.1 变负荷过程仿真

按照本文的方法设计基于调度信号的一阶前馈补偿自抗扰控制器（记为前馈补偿增益调度ADRC）并进行仿真。同时，为比较说明本文设计的效果，分别设计了不带前馈的增益调度补偿自抗扰控制器（记为增益调度补偿ADRC）和仅带补偿环节的自抗扰控制器（记为补偿ADRC），以考察比较前馈作用和变参数设计的效果。

其中，前馈控制器根据Qγ和uγ的对应关系，按照分段线性化的方式进行设计，并取Kf=0.5。

根据式（23）的变工况模型信息，按照式（19）—（21）设计和整定反馈控制器，按照式（14）—（15）设计和整定惯性补偿环节，按照式（16）—（18）设计和整定扩张状态观测器，从而获得前馈补偿增益调度ADRC 和增益调度补偿ADRC。补偿ADRC 的参数不随调度指令变化，因此按照文献［18］的方法根据额定负荷的模型信息进行设计。

设置仿真计算周期为ΔT=0.2 s，令工况值先阶跃减小然后再阶跃增加，设定值跟随工况变化，变化速率为0.055 min。在负荷变化时，仿真获得的主蒸汽压力和给煤量变化曲线分别如图4—5 所示。从图中可以看出。

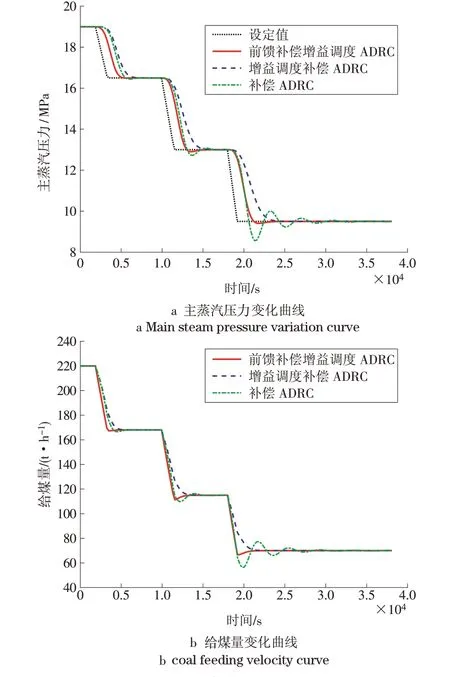
图4 降负荷过程响应曲线Fig.4 Response curve in derating process

（1）基于调度信号的前馈补偿ADRC 无论是在高负荷段、中负荷段还是低负荷段，均能快速平稳地跟踪设定值的变化，调节时间明显快于另外2 种控制方法。

（2）当仅取消前馈作用时，由于此时控制器参数能够随负荷变化，因此在不同工况下均表现出较为一致的平稳控制效果，但由于没有前馈控制器而是完全依靠反馈作用进行调节，因此响应速度明显慢于有前馈补偿的自抗扰控制器。

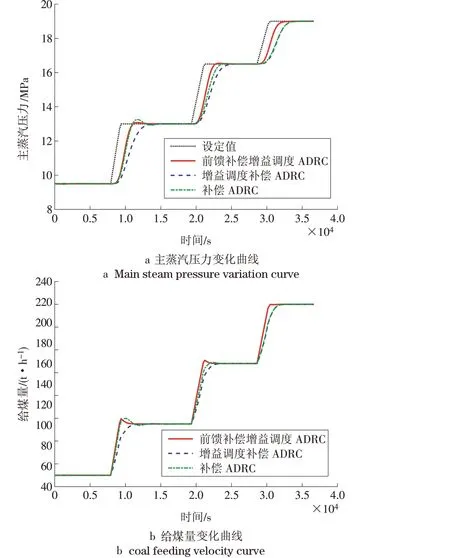
图5 升负荷过程响应曲线Fig.5 Response curve in load-up process

（3）当取消前馈控制器且控制器参数不随调度信号改变时，ADRC 的被控量在高负荷段能较为平稳地跟踪设定值的变化，但由于没有调度机制，控制参数不随工况而变化，因此在低负荷段呈现出明显较大的超调量。

从图4—5的比较结果可以看到，在工况大范围变化时，本文设计的基于调度信号的前馈补偿ADRC 在各负荷下均能够表现出较为一致且满意的控制效果，显示出优异的工况适应性和优良的控制效果。

3.2 性能鲁棒性仿真

本文控制器的设计采用了被控过程在多个工况下的动态模型信息，但实际上控制器设计所依据的模型信息往往与实际有偏差，因此需要评价无法精确建模的情况下，控制器的性能鲁棒性。

令模型参数发生±20%的变化且服从均匀分布，控制器参数保持不变，设定值分别从9.5 MPa阶跃到13.9 MPa，以及从16.5 MPa 阶跃到19.0 MPa，进行2 000 次仿真并计算超调量和调节时间的指标分布情况，测试控制系统在低负荷和高负荷下的性能鲁棒性（如图6所示）。从图中可以看出。

图6 设定值阶跃下的性能鲁棒性比较Fig.6 Comparison of the robust performance at set-point step

（1）当获取的模型信息不准确时，补偿ADRC在低负荷段的超调量和调节时间的分布较为分散，性能鲁棒性较差，而在高负荷段的性能鲁棒性有所提高。

（2）无论在低负荷段还是高负荷段，增益调度补偿ADRC 的超调量基本不超过5%，调节时间略慢，但低负荷段和高负荷段的调节时间变化不大，性能指标分布都相对集中，显示出很好的性能鲁棒性。

（3）前馈补偿增益调度ADRC 的调节时间有明显改善，且调节时间的性能鲁棒性相对较好，但在高负荷段超调量较大且分布比较分散。进一步仿真发现，减小前馈权重系数Kf将使得超调量的鲁棒性能有所改善；当Kf取为0 时等同为增益调度补偿ADRC。因此若希望被控过程的超调量较小，当存在模型不确定性时，前馈控制作用不宜太强。

4 结束语

为了提高燃煤机组在宽负荷频繁调峰下的控制性能，本文针对大惯性非线性热力过程，利用被控过程在各工况下的动态模型信息，设计了基于调度信号变参数的前馈补偿自抗扰控制器。由于前馈控制器、反馈控制器、补偿环节和扩张状态观测器的控制参数均根据调度信号实时变化以适应不同工况下的动态特性，因而提高了自抗扰控制器对系统大惯性和变工况的适应能力。仿真算例验证了方法的可行性和有效性。控制器结构相对简单，便于参数整定和现场实现，显示出良好的实际应用前景。