考虑风电机组虚拟惯量的新型电力系统频率分布式模型预测控制策略

屈涛涛，綦晓*，蒋文珂，杜鸣，潘岩

（1.暨南大学能源电力研究中心，广东珠海 519070；2.华北电力大学国家能源发展战略研究院，北京 102206；3.长沙有色冶金设计研究院有限公司研发中心，长沙 410019）

0 引言

为推进能源转型以实现“双碳”目标，风电等新能源得到大力发展。截至2021年年底，我国风电并网装机容量已突破300 GW［1］。然而，自然界中风能的随机性和波动性导致风电具有较强的不确定性；风电机组与电网频率解耦，在频率扰动下无法为电网提供惯量支撑，削弱了系统等效惯量，这给电力系统调频带来了挑战［2-4］。

大规模风电并网导致系统等效惯量大幅降低、系统源侧不确定性增加，而风电机组主动频率支撑是解决系统等效惯量降低的重要途径之一。目前，风机参与调频的控制方法主要包括超速控制［5-6］、变桨控制［7-9］、虚拟惯量控制（Virtual Inertia Control，VIC）［10-11］和功率定值控制［12］。其中，超速控制和变桨控制的基本思路是使风机偏离最大功率跟踪（Maximum Power Point Tracking，MPPT）状态，预留部分功率参与调频，但该方法降低了发电经济性。而VIC和功率定值控制主要通过释放风机的转子动能参与调频，风机无需偏离MPPT 运行状态，但该方法仅提供短时间尺度内的频率支撑。

为抑制系统源侧不确定性对系统频率的干扰，各类先进控制算法，如模型预测控制（Model Predictive Control，MPC）、自抗扰控制［13］和滑模变结构控制［14-15］等，相继在新型电力系统频率控制领域得到应用。基于预测模型和滚动时域优化特点的MPC 因能在有限时域内求得控制动作最优解，而受到部分学者的青睐。文献［16］以四区域含风电的电力系统为研究对象，构建其整体预测模型，设计了集中式MPC。由于采用的是整体系统模型，其控制效果可以实现全局最优；但计算量较大，不利于控制的实时性。文献［17］考虑单个区域本地信息建立预测模型并设计分散式MPC 控制器。相比集中式MPC，其计算量更小且可靠性更高；但仅利用本地信息难以实现各区域之间的高效协同，系统整体控制效果相对较差。文献［18-20］在分散式MPC的基础上增加了通信网络，在本地控制器中充分考虑了各区域间的耦合项，设计了分布式MPC（DMPC），其控制效果能实现全局最优且兼具分散式MPC的可靠性。

目前，各类MPC 频率控制器基本不考VIC 对控制性能的影响，对VIC 过程中MPC 的预测精度产生干扰，削弱了控制效果。本文针对以风电为主体的多区域新型电力系统，设计了VIC环节，利用风电机组转子动能参与调频；其次，考虑VIC的影响重构预测模型，提升预测精度。根据上述预测模型设计考虑VIC的DMPC，有效补偿VIC过程对二次调频的干扰。

1 新型电力系统调频模型构建

1.1 风电机组模型

风电机组通常包含气动系统、传动系统、变桨系统、电气系统和控制系统等子系统，由于本文仅考虑风机运行在额定风速下的情况，因此模型中不含变桨系统，其框架结构如图1所示。其中：Pm为风电机组获取的机械功率；Pe为发电机输出的电磁功率；CP为风能利用系数；r为风力机叶片半径；v为输入的风速；Pf为风机辅助频率控制指令；ΔT为电磁功率与机械功率的转矩差；ω为风机转速；Kc为MPPT 最优跟踪系数；Jw为风电机组转动惯量；Te为逆变器响应时间常数；Pω为额定风速下时的风机运行功率。

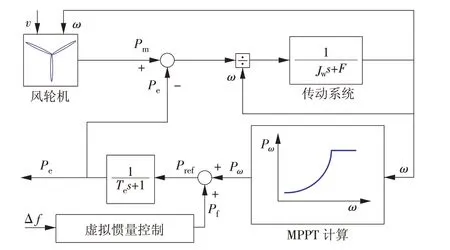
图1 风电机组模型Fig.1 Model of a wind turbine

式中：ρ为空气密度。

气动系统获得的机械功率通过传动系统传送至电气系统，单质块传动系统模型如下

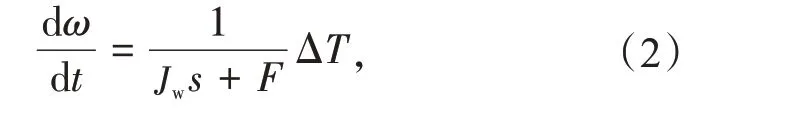
式中：ΔT= (Pm-Pe)ω。

当风机运行在额定风速下时，受MPPT 控制，其功率表示为

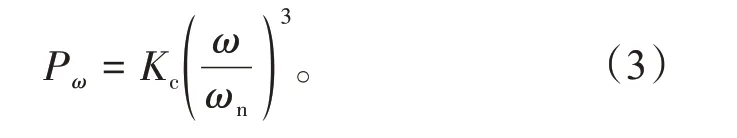
式中：ωn为风电机组最大转子转速。

最终，经过逆变器输出的电磁功率为

为简化模型，通过文献［24］的方法对上述模型进行线性化处理可得

式中：状态变量xw=[ΔωΔPe]，Δω，ΔPe分别为风电机组转子转速变化量和电磁功率变化量；输出变量uw= ΔPf为辅助调频指令变化量；输出变量yw= ΔPe；Aw为状态转移矩阵；Bw为输入矩阵；Cw为输出矩阵。

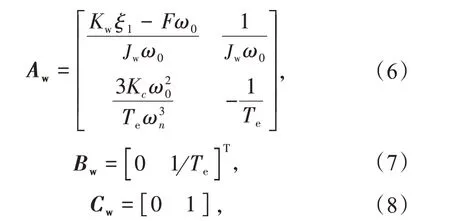
1.2 电力系统调频模型

本文以含风电的四区域电力系统为研究对象，搭建电力系统调频模型。以火电机组为调频模型，主要包括调速器模型，再热锅炉模型和汽轮机模型［25-26］，输出变化量分别见式（9）—（11）。由于火电机组调频模型已经较为成熟，此处不再赘述。

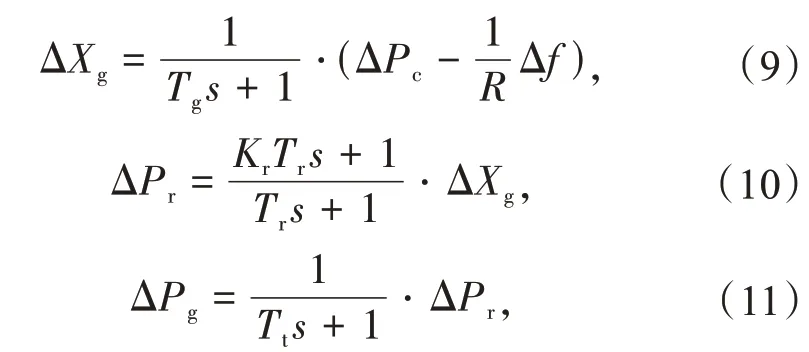
式中：ΔPc，ΔXg，ΔPr，ΔPg分别为控制信号、调速器、再热锅炉和汽轮机的输出变化量；Tg，Kr为调速器响应时间常数和再热锅炉增益系数；Tr，Tt为再热锅炉响应时间常数和调速器响应时间常数；R为火电机组调速器下垂系数。

在互联电力系统区域i中，有功功率的不平衡量将导致频率的波动，该过程可表示为

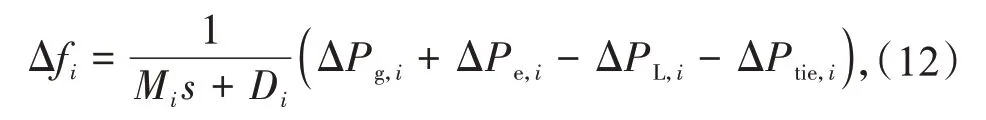
式中：Δfi为第i个区域的频率偏差；Mi和Di分别为第i个区域的惯量常数和阻尼常数；β为频率偏差系数；ΔPtie，i，ΔPg，i，ΔPe，i，PL，i分别为第i区域的联络线功率、汽轮机输出功率、风电机组输出电磁功率和负荷的变化量。

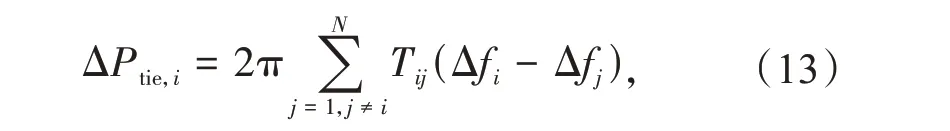
因此，区域i的区域控制误差为式中：Tij为等效力矩系数。

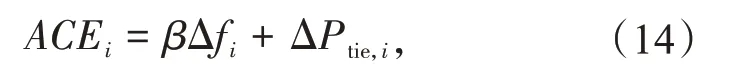
综上所述，互联电力系统区域i调频模型如图2所示（Ri为区域i火电机组下垂系数），模型可表示为

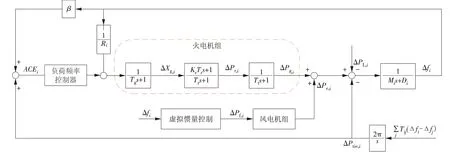
图2 区域i电力系统调频模型Fig2 Frequency regulation model of area i of the power system

2 控制器设计

2.1 VIC环节

目前，风电机组依靠大量的电力电子器件接入电网，致使风电机组和电网频率解耦，无法主动为系统提供频率支撑。针对上述问题，本文为风电机组设计VIC 环节，以释放风电机组的转子动能参与系统调频。VIC 过程可分为2 个部分：（1）模拟传统机组的下垂特性，即下垂控制过程，ΔPf为功率补偿指令Pf的变化量，见式（16）；（2）模拟传统机组的机械惯性，即惯量控制，ΔPf见式（17）。

式中：Kp和Kd分别为VIC的比例和微分系数。

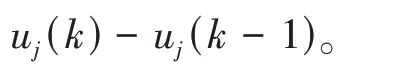
为推导系统预测方程需做出假设：除控制时域（m）外，其他控制量不变（p为预测时域），

Δui(k+i) = 0，i=m，m+ 1，…，p- 1。

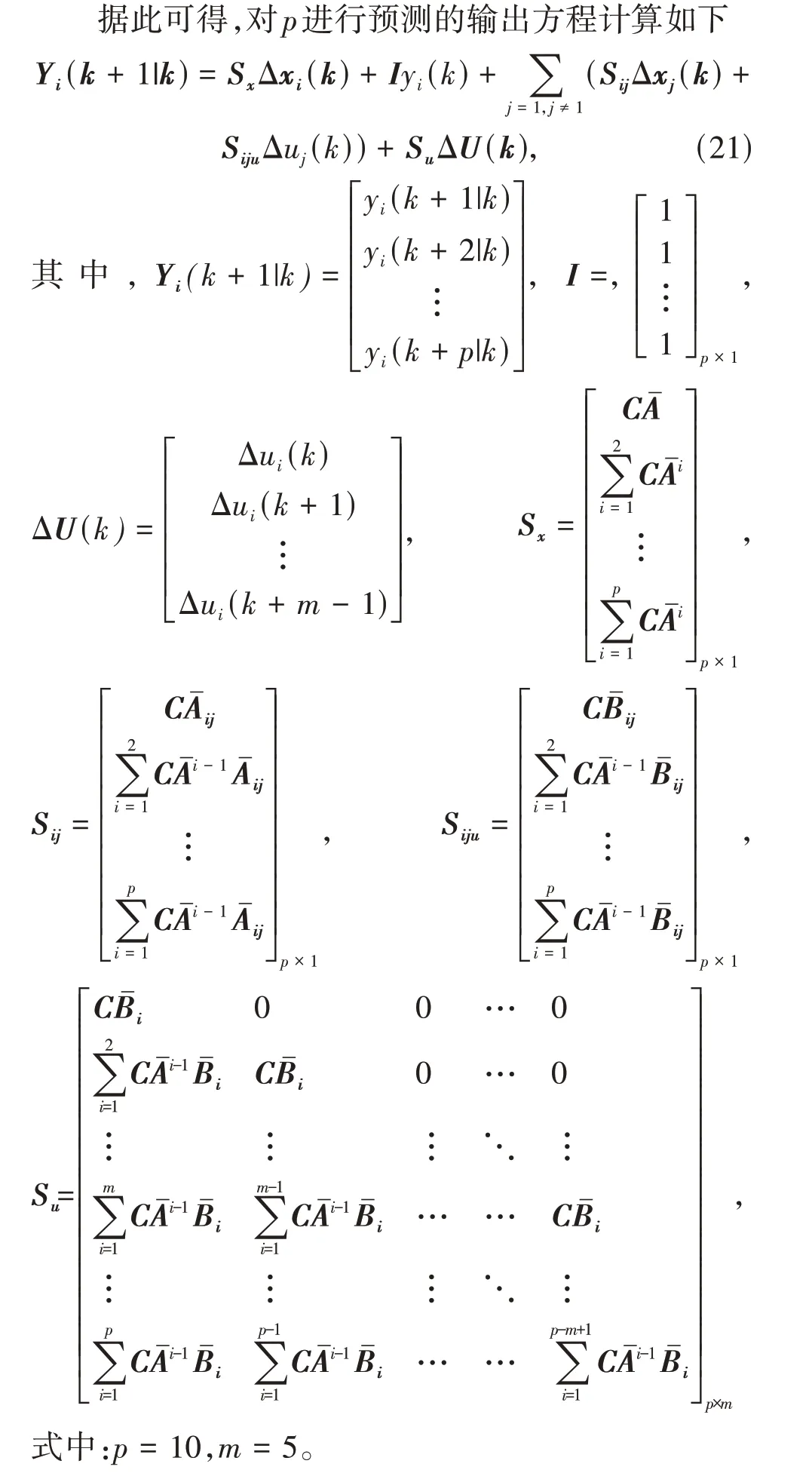
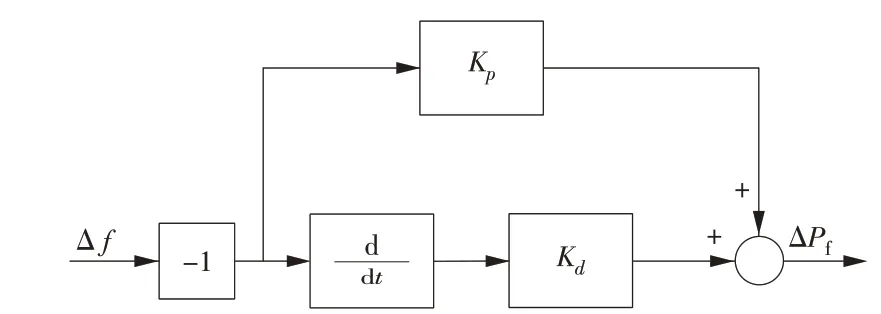
图3 虚拟惯量控制Fig.3 Virtual inertia control

2.2 DMPC控制器设计

风电机组的加入增强了电力系统源侧的不确定性，常规的调频策略难以满足现在的调频需求。MPC 基于模型预测和滚动优化的特点，能实时得到较优的控制信号，较传统比例积分（PI）控制器优势显著。因此，本文采用MPC 作为电力系统的二次调频控制器，其基本控制框架如图4所示（k为时刻）。

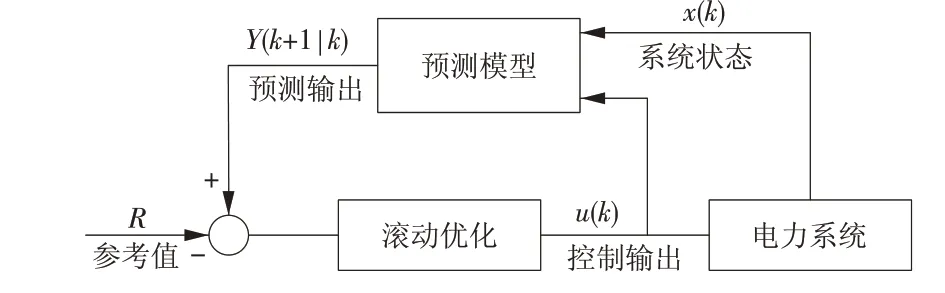
图4 MPC框架Fig.4 Block of MPC

基于式（15）的模型设计DMPC 频率控制器，首先，将式（15）离散化可得

2.2制动,饮水。医护指导患者卧床制动,一切日常活动都有家属协助在床上进行,床头控制在30度以下,其次加大饮水量,每日饮水量达到3000ml以上,通过多饮多排冲洗尿道,避免血块杜塞,但任然每天堵管2-3次,经过医生的手动进行膀胱冲洗苏通尿管,尿管恢复通畅,尿管及肾造瘘均引流出暗红血色尿液,每天尿液总尿量3300ml~5400ml。

对于控制器目标函数的设定，一方面需要考虑让被控输出接近参考输入，另一方面需要让控制动作变化不要太大。因此，可设定如下目标函数

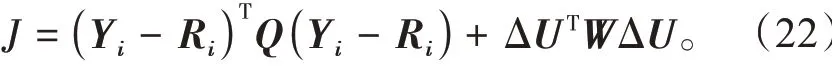
式中：Ri为输出参考值；Q和W分别为被控输出偏差和控制信号变化量的系数加权矩阵。

将式（21）代入式（22），求解最优控制增量序列

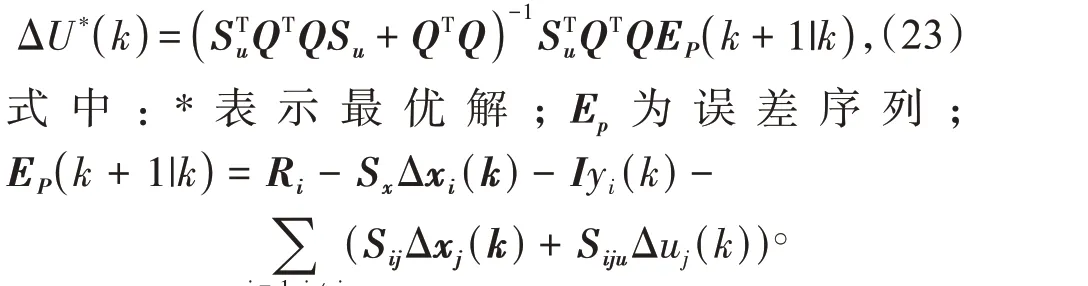
取ΔU*(k)中第1个元素Δu(k)加上上一时刻控制器输出u(k- 1)作为控制器输出。至此，一个采样时刻控制动作完成。到下一个采样时刻，其控制时域向前推移一个时刻，重新计算EP，如此循环往复，实现滚动优化。

2.3 考虑VIC的DMPC控制器设计

根据上节的模型设计了单个区域的MPC 控制器，但该模型中并未考虑到风电机组VIC过程，本节将针对该问题重构MPC 预测模型，以提高模型预测精度。首先，将式（12）代入式（18）可得

基于重构模型重复步骤（19）—（23）的推导，即可完成单个区域考虑VIC 的DMPC 频率控制器设计，此处不在进行赘述。

3 仿真与分析

表1 仿真参数Table 1 Parameters of the simulation

3.1 负荷阶跃扰动下系统响应分析

令区域1负荷在20 s处发生标幺值为+0.2的阶跃扰动，区域3负荷在100 s处发生标幺值为+0.1的阶跃扰动，如图5 所示，分别对考虑VIC 和不考虑VIC 的DMPC 策略进行仿真，各区域频率偏差响应仿真结果如图6所示，20 s处区域1的仿真结果对比见表2。

表2 20 s处阶跃扰动下区域1仿真结果对比Table 2 Comparison of disturbance simulation data at 20 s

图5 负荷阶跃扰动Fig.5 Load step disturbance

如图6 所示，当区域1 受到阶跃负荷扰动后，基于考虑虚拟惯量的DMPC 的系统中区域1 频率偏差最低点为-0.003 2 Hz，其相邻两区域的频率偏差最低点约为-0.000 21 Hz；而基于常规DMPC 的系统中区域1 频率偏差最低点为-0.006 4 Hz，2 区、4 区域频率偏差最低点约为-0.000 42 Hz，且超调也更大，验证了所提策略相比常规DMPC 具有更好的控制性能，可有效提高频率最低点。当区域3 受到阶跃负荷扰动后，基于所提策略控制的系统中区域3频率偏差最低点为-0.001 5 Hz；而常规DMPC 系统中区域3 频率偏差最低点为-0.002 6 Hz，这进一步证明了所提策略的有效性。

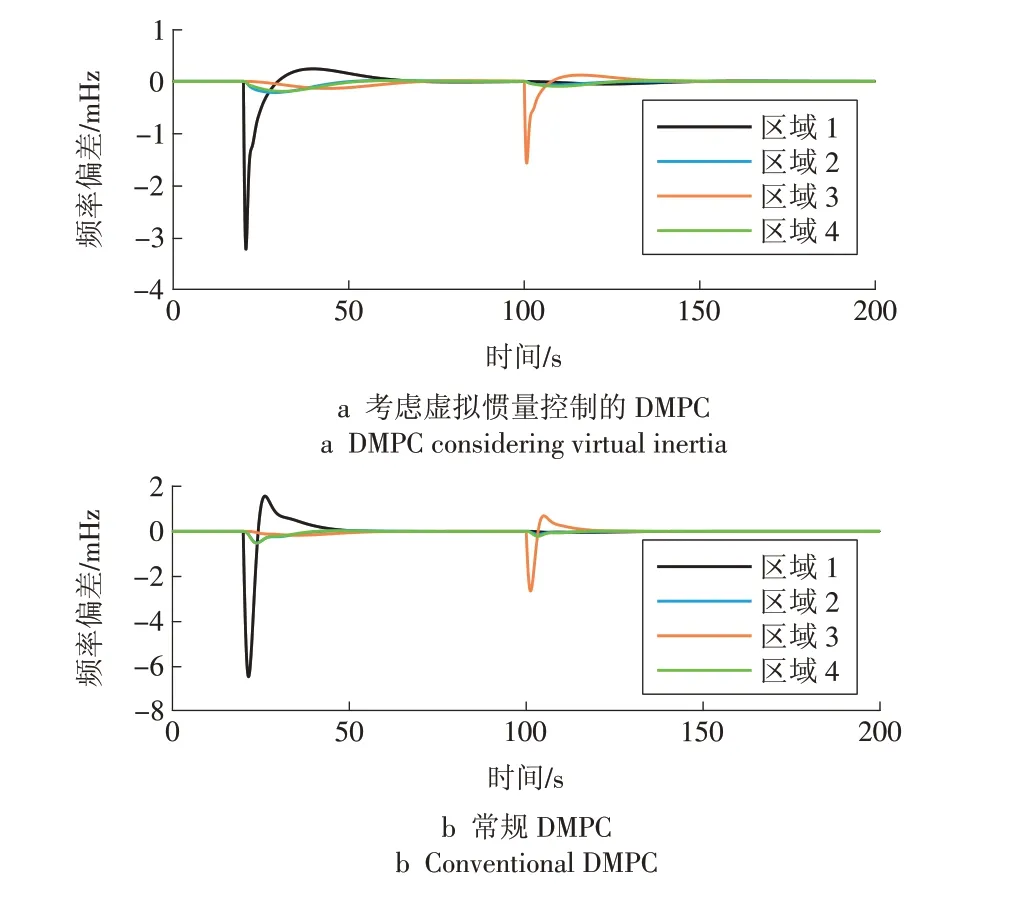
图6 负荷阶跃扰动下各区域频率偏差响应仿真结果Fig.6 Simulation results of frequency deviation responses under load step disturbance in each area

相比常规DMPC，所提策略可有效减少对风电功率的调用，同时降低了从系统中吸收功率的最大值，可以减少风机转速恢复过程中频率二次跌落的风险，如图7所示。图8为2种策略下各区域火电机组功率响应仿真，结果显示本文所提策略可有效提高火电机组响应速度。

图7 负荷阶跃扰动下各区域风电机组电磁功率响应仿真结果Fig.7 Simulation results of electrical power responses of wind turbine under load step disturbance in each area

图8 负荷阶跃扰动下各区域火电机组功率响应仿真结果Fig.8 Simulation results of power response of thermal power units under load step disturbance in each area

3.2 随机负荷扰动下系统响应分析

令区域1 受到标幺值为-0.1～0.1 的随机负荷扰动，如图9 所示，则区域1 频率响应、风电机组与火电机组的功率响应如图10—12所示。

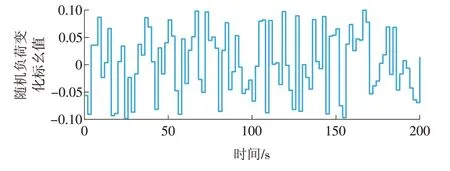
图9 区域1随机负荷扰动Fig.9 Random load disturbance in area 1

图10 随机负荷扰动下区域1频率响应仿真结果Fig.10 Simulation results of frequency deviation responses under random load disturbance in area 1

由图10可知，本文所提策略控制的系统最大频率偏差为0.002 4 Hz，常规MPC 的系统最大频率偏差为0.006 2 Hz，且整个时间段内本文所提策略频率波动幅值均比常规MPC 幅值更小，进一步验证了本文所提策略的优越性。由图11可知，本文所提策略相比常规DMPC可有效减少风电功率参与调频最大功率，同时减少从系统吸收的功率，可降低频率由于风机过度参与调频导致的二次扰动问题的影响。由图12可知，本文所提策略火电机组功率响应速度更快。

图11 随机负荷扰动下区域1风电功率响应仿真结果Fig.11 Simulation results of wind power responses under random load disturbance in area 1

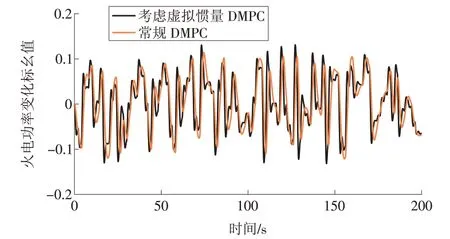
图12 随机负荷扰动下区域1火电机组功率响应仿真结果Fig.12 Simulation results of power response of thermal power units under random load disturbance in area 1

4 结论

针对风电机组VIC 过程对DMPC 频率控制的干扰问题，本文提出了一种考虑虚拟惯量控制的DMPC 频率控制策略。充分考虑虚拟惯量控制过程对DMPC的影响，重构其预测模型，根据重构模型设计DMPC频率控制器，提高了预测精度，使其控制性能得到提升。最后，与常规MPC 进行对比，本文所提策略可有效提高频率性能，且能降低频率由于风机过度参与调频导致的二次扰动问题。