电动汽车永磁同步驱动电机控制器用变权重叠加型过调制方法*

林 程，蒋雄威，庄兴明，刘焕然，邢济垒，高 帅

（1.北京理工大学机械与车辆学院，北京 100081；2.北京华锋新能源技术研究院有限公司，北京 100081）

前言

永磁同步电机因具备高功率密度和高可靠性的特点，故在电动汽车驱动电机领域被广泛应用［1］。在众多电机控制调制方法中，空间矢量脉宽调制（space vector pulse width modulation，SVPWM）具有电压利用率较高、易于工程应用等优点，是电动汽车驱动电机广泛采用的调制方法［2-4］。但SVPWM的电压利用率并不能达到最大，导致驱动电机在高转速时的转矩输出能力和转速调节能力受到限制［5-7］。应用过调制方法能够进一步提高电压利用率，从而加强驱动电机转矩输出能力和转速调节能力［8］。然而很多传统过调制方法在过调制Ⅱ区中存在调制电压突变的问题。

比亚迪汽车提出了一种电动汽车电机控制器用的过调制控制方法，以开关时间作为判据进行直流母线电压的非线性调制。该方法消除了线性调制与过调制之间的界限，且计算量小，易于工程应用。但该方法在过调制Ⅱ区存在电压突变，使电机输出转矩抖动较大，影响电动汽车动力输出性能和NVH性能。

文献［9］中提出了过调制领域经典的双模式控制方法，根据调制系数大小将过调制区域划分为过调制Ⅰ区和Ⅱ区。该方法在整个过调制区域内都具有较小的谐波畸变率和较好的线性化增益，但是该方法计算量大，不适合工程应用。文献［10］中用两段电压矢量进行加权计算，得到调制电压矢量轨迹，计算量小且易于数字化实现。但是，由于加权分量的突变，导致该方法在过调制Ⅱ区存在较大电压突变，谐波畸变率和电机抖动较大。文献［11］中将过调制区域内的调制电压裂变为两个不同参数正弦波的衔接，通过衔接点坐标的理论计算，保证了调制电压基波与调制系数的严格线性化关系。同时，该方法对调制波和PWM波进行了较为详细的谐波分析。但是该方法中，裂变后两个正弦波的相位参数和幅值参数的计算过程复杂，难以适应工程应用需求。文献［12］中通过电压调制六边形的顶点和内切圆的交叉组合构成调制电压轨迹，内切圆轨迹在一定程度上减小了调制电压的谐波畸变率，但由于内切圆轨迹与六边形顶点之间的不连续性，导致调制电压的幅值和相位角存在突变。文献［8］中采用矢量角度线性变化策略，提出了改进型同步SVPWM过调制方法，算法简单、计算量小，实现了全速度范围内不同速度段的平稳运行。但该方法没有考虑电压调制系数的线性增益效果，调制电压在过调制Ⅱ区也存在较大突变。

针对传统过调制方法在过调制Ⅱ区存在调制电压突变的问题，本文中基于叠加原理，将参考电压矢量相位角引入叠加权重因子的计算，消除了调制电压的突变，在提升电动汽车转矩输出能力和转速调节能力的基础上，降低了电压谐波畸变率，提高了电机控制的电流稳定性，减小了电机输出转矩的抖动。

1 过调制控制方法原理概述

电动汽车驱动电机控制器用三相两电平电压型逆变器，如图1所示。图中g表示动力电池中性点，也是系统接地点，n表示电机绕组中性点，abc表示电机三相绕组与电机控制器的连接点，Sabc和S'abc表示电机控制器中的功率开关，以IGBT为主，能够提供0和Udc两种电平。

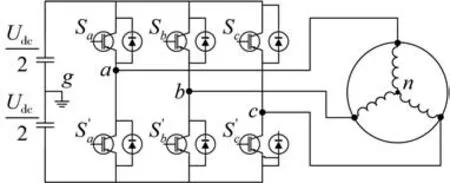
图1 三相两电平电压型逆变器

1.1 提升驱动系统最大输出功率

点abc与中性点n之间的电势差就是电机的相电压Uabc。电机控制器的主要作用就是将动力电池的直流端母线电压Udc逆变为电机的三相交流相电压Uabc。相电压基波幅值越大，动力电池提供的母线电压的利用率就越高，电机转矩输出能力和转速调节能力就越强。

六拍阶梯波工况是电机控制器理论极限状态，此时电机相电压的基波幅值为2Udc∕π。为定量描述电压利用率，将参考电压矢量幅值与2Udc∕π的比值定义为调制系数MI：

式中：|Us|为参考电压矢量幅值；Udc为直流母线电压。

不难得出，调制系数MI取值范围为[0，1]，且调制系数越大，母线电压利用率就越高。传统SVPWM方法仅能工作在如图2所示电压调制六边形的内切圆内部，调制系数最大只能达到MI=0.9069，母线电压利用率偏低，电机在高转速区域内的转矩输出能力和转速调节能力都受到限制。

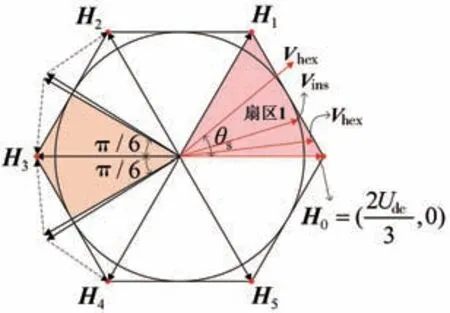
图2 电压调制六边形

为达到更高的电压利用率，过调制方法逐渐成为电动汽车电机控制器优化算法的研究重点［13］。利用过调制方法，调制系数最大能达到MI=1，电压利用率可比传统SVPWM算法提升10.3%。如图3所示，过调制算法拓宽了电机外特性曲线范围：电机最高转速从n1提升到n2；电机高转速区域内的任意转速nh对应的最大转矩从T1提升到T2，意味着过调制方法能够提升电动汽车驱动系统最大输出功率，使电动汽车驱动电机在高转速区域内拥有更强的转矩输出能力和转速调节能力。

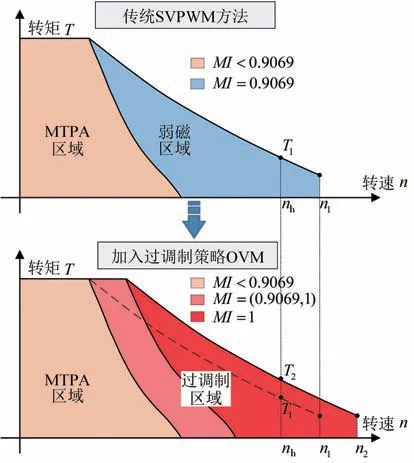
图3 过调制方法拓宽电机外特性曲线范围

1.2 过调制Ⅱ区电压突变

根据调制系数MI的大小，过调制区域分为过调制Ⅰ区（0.9069≤MI＜0.9517）和 过 调 制Ⅱ区（0.9517≤MI≤1）。

过调制Ⅰ区中，仅须调节参考电压矢量的幅值，相位角可保持ωt连续变化，所以过调制控制方法在过调制Ⅰ区具有良好的性能表现，但电压利用率被限制在MI=0.9517的水平；为更大限度地提升电压利用率，使电机驱动系统能输出更大的功率、具备更高的转矩输出和转速调节能力，过调制方法有必要向过调制Ⅱ区进行扩展。然而在过调制Ⅱ区中，电压矢量的幅值和相位角均须调节，调制电压突变的问题变得尤为严重，导致调制电压谐波畸变率和电机输出转矩抖动增大，影响电动汽车电机驱动系统动力输出性能和NVH性能。因此，如何解决过调制Ⅱ区中调制电压突变的问题成为过调制控制方法研究的重点［5］。

2 变权重叠加型过调制方法

为解决过调制Ⅱ区中存在的调制电压突变问题，提出基于叠加原理的变权重叠加型过调制方法，将参考电压相位角引入叠加权重因子计算，消除叠加分量发生跳变带来的影响，解决了调制电压突变的问题。

如图2所示，当MI=0.9069时，调制电压矢量轨迹为六边形的内切圆，电压矢量表示为Vins；当MI=0.9517时，调制电压矢量轨迹为六边形边界，电压矢量表示为Vhex；当MI=1时，调制电压矢量轨迹为六边形的6个顶点，电压矢量表示为Hi，其中i=0，1，…，5。

2.1 叠加过程

叠加原理的核心思想就是根据与调制系数相关的叠加权重因子，在过调制Ⅰ区和过调制Ⅱ区分别对两组不同的加权分量进行加权计算，加权分量从上述3个电压矢量Vins、Vhex和Hi中选择。具体确定规则如下：

过调制Ⅰ区时，加权分量是Vins和Vhex，且与参考电压矢量同相位；过调制Ⅱ区时，加权分量是Vhex和Hi，其中Vhex与参考电压矢量同相位，Hi的确定方法是：当参考电压矢量相位角处于某一Hi矢量前后π∕6范围内时，则加权分量取该Hi矢量；超出π∕6范围则取下一个Hi矢量。如图2所示，H3前后π∕6的范围内，加权分量取Hi=H3；超出π∕6范围则取Hi=H4或Hi=H2；其他情况以此类推。

过调制Ⅰ区中，叠加权重因子kⅠ及调制电压矢量Vr计算公式分别为

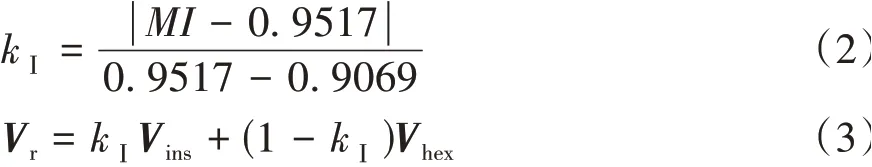
由于Vins和Vhex的轨迹都具有连续性，所以调制电压矢量Vr也具有连续性，不会发生突变。

然而，在过调制Ⅱ区如果沿用式（2）和式（3）的方法确定权重因子kⅡ和调制电压矢量Vr，即

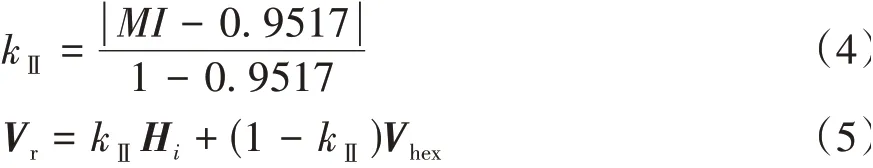
则会造成调制电压矢量突变。

以扇区1为例，图4所示为θs=π∕6时的叠加过程。其中，图4（a）为θs=(π∕6)左极限时刻，此时Hi=H0，通过式（5）加权计算得到的调制电压矢量Vr如图中红色箭头所示；图4（b）为θs=(π∕6)右极限时刻，此时加权分量Hi从H0跳变为H1，加权得到的调制电压矢量Vr如图中红色箭头所示。扇区1中调制电压轨迹如图中蓝色线段所示。不难看出，由于加权分量Hi在离散点H0与H1之间切换，导致加权得到的调制电压存在突变。

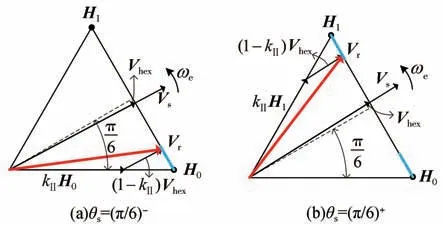
图4 传统方法叠加过程（存在突变）

2.2 叠加权重因子重构

为消除过调制Ⅱ区加权分量Hi的跳变对调制电压的影响，将参考电压相位角θs引入Hi的叠加权重因子计算，在式（4）的基础上重构叠加权重因子kopt。以扇区1为例，新定义的权重因子kopt为取θΔ=kⅡπ∕6，则式（6）可以改写为

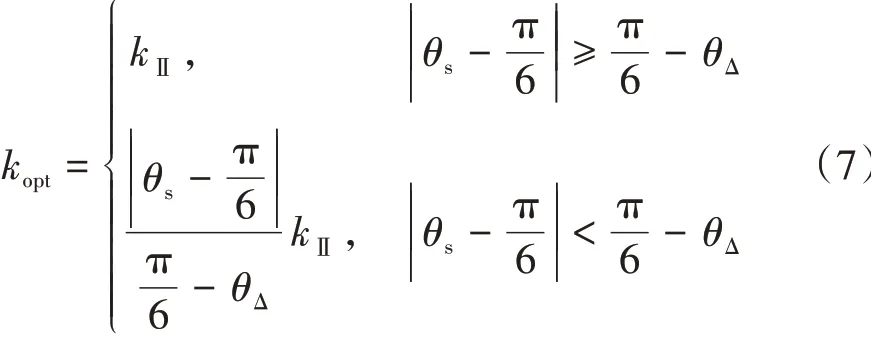
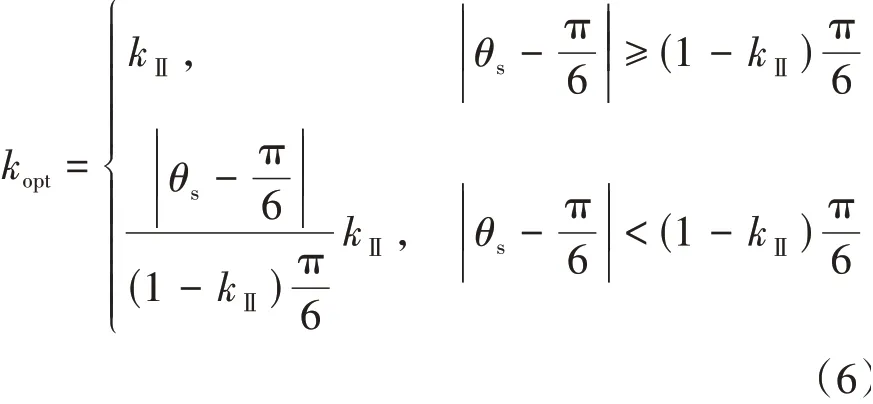
将kopt代入式（5）得

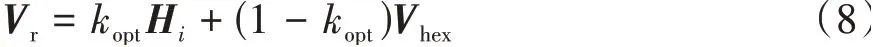
由式（8）可知，当Hi的叠加权重因子kopt=0时，Hi在不同离散点之间的跳变将不会导致调制电压Vr的突变。

根据式（7）得到的kopt关于θs和MI的函数图像如图5所示。在过调制Ⅱ区中，对于任意调制系数MI，当θs趋近π∕6时，Hi的叠加权重因子kopt都趋近于零，消除此时Hi在不同离散点间跳变带来的影响，保证调制电压矢量轨迹的连续性，消除调制电压矢量的突变。

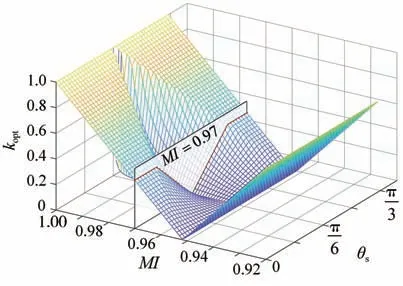
图5 kopt关于θs和MI的函数图像

具体叠加过程如图6所示。以扇区1为例，当θs=(π∕6)-时，Hi=H0，叠加权重因子趋近于0，所以此时调制电压矢量Vr趋近于Vhex；当θs=(π∕6)+时，Hi发生跳变，取Hi=H1，由于叠加权重因子趋近于0，Hi的跳变不会影响加权结果，所以此时调制电压矢量Vr仍然趋近于Vhex，没有发生突变。此后，叠加权重因子逐渐增加至原始值，所以调制电压轨迹是H0和H1之间的连续线段，如图中蓝色线段所示，其他扇区以此类推。

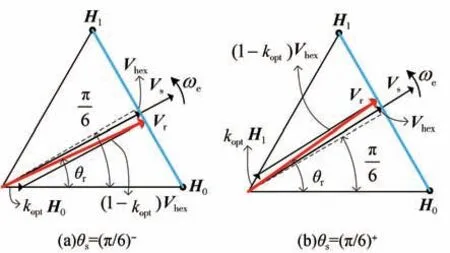
图6 本文方法叠加过程（无突变）

2.3 过渡平顺性分析

对提出的变权重叠加型过调制方法中过调制Ⅰ区与过调制Ⅱ区、过调制Ⅱ区与六拍阶梯波工况过渡过程的平顺性进行分析。

在图5中，三维曲面与MI=0.97平面的交线是MI=0.97时叠加权重因子kopt的函数图像，如图7中关于θs=π∕6左右对称的红色分段线条所示。当θs∈[0，θΔ)时，kopt保 持 初 始 值kⅡ不 变；当θs∈[θΔ，π∕6)时，kopt从初始值kⅡ线性下降至0，消除加权分量Hi跳变带来的影响。

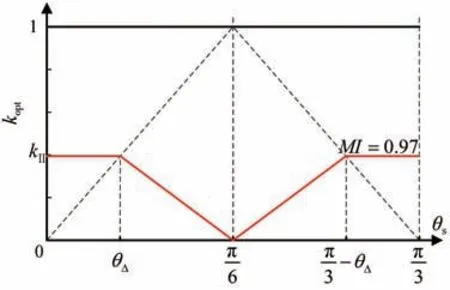
图7 kopt函数图像（MI=0.97）

图像拐点θΔ=kⅡπ∕6与叠加权重因子初始值kⅡ成正比，当MI=0.9517时，由式（4）可得kⅡ=0，则图像拐点θΔ=kⅡπ∕6=0，所以kopt≡0，代入式（8）可得Vr≡Vhex，对应的调制电压轨迹为六边形边界，该轨迹也是过调制Ⅰ区上边界的电压轨迹，证明该方法能实现过调制Ⅰ区和过调制Ⅱ区之间的平滑过渡；当MI=1时，由式（4）可得kⅡ=1，则图像拐点θΔ=kⅡπ∕6=π∕6，所 以kopt≡1，代 入 式（8）可 得Vr≡Hi，对应的调制电压轨迹为电压调制六边形的顶点，证明该方法能实现六拍阶梯波工况运行。

2.4 谐波畸变率对比分析

将调制电压轨迹向α轴投影可以得到相电压调制波形，通过快速傅里叶变换得到调制电压的谐波畸变率，如图8所示。

以调制系数MI=0.97为例，图8（a）为传统方法的调制电压波形，图像左侧为调制电压矢量轨迹，图像右侧为投影得到的1∕4电周期内的相电压波形，如图中红色线条所示。不难看出，传统叠加方法调制电压轨迹不连续，调制电压矢量存在突变，图中红色阴影部分为突变范围；投影后得到的相电压波形不连续，存在突变，导致谐波畸变率较高。图8（b）为传统方法相电压经过快速傅里叶变换得到的频谱图，总谐波畸变率THD=12.95%。

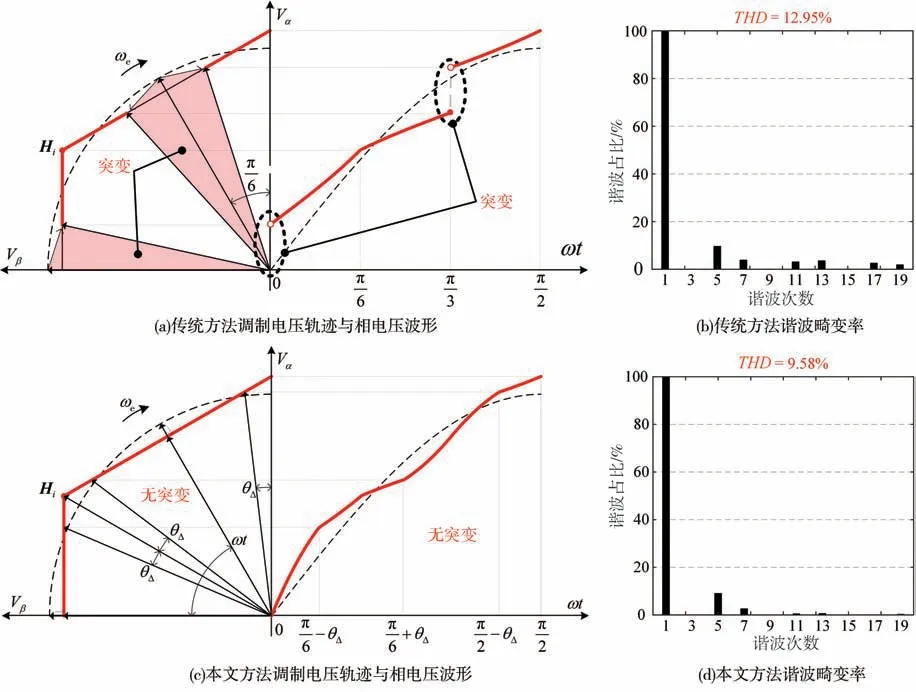
图8 传统方法与本文方法调制电压轨迹、相电压波形以及谐波畸变率（MI=0.97）

图8（c）为本文提出的变权重叠加型过调制方法的调制电压波形，图像左侧为调制电压轨迹，图像右侧为投影得到的1∕4电周期内的相电压波形，如图中红色线条所示。可以看出，本文方法调制电压轨迹连续，调制电压矢量不存在突变，相电压波形也不存在突变，提升了相电压基波含量，降低了谐波畸变率。图8（d）为本文方法相电压经过快速傅里叶变换得到的频谱图，总谐波畸变率降低至9.58%。

图9为本文方法与传统方法的谐波畸变率对比。由于本文方法通过引入参考电压矢量相位角进行叠加权重因子重构计算，消除了调制电压突变，所以在过调制Ⅱ区内的谐波畸变率小于传统方法。

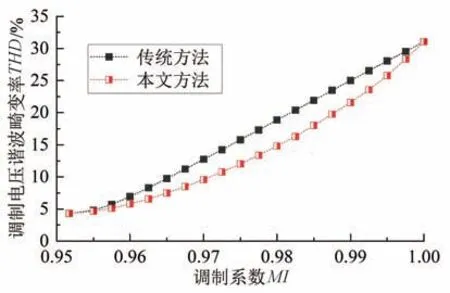
图9 谐波畸变率对比

3 仿真与试验结果分析

根据前文提出的变权重叠加型过调制方法，基于Simulink仿真和台架试验进行验证，所用电机参数如表1所示。

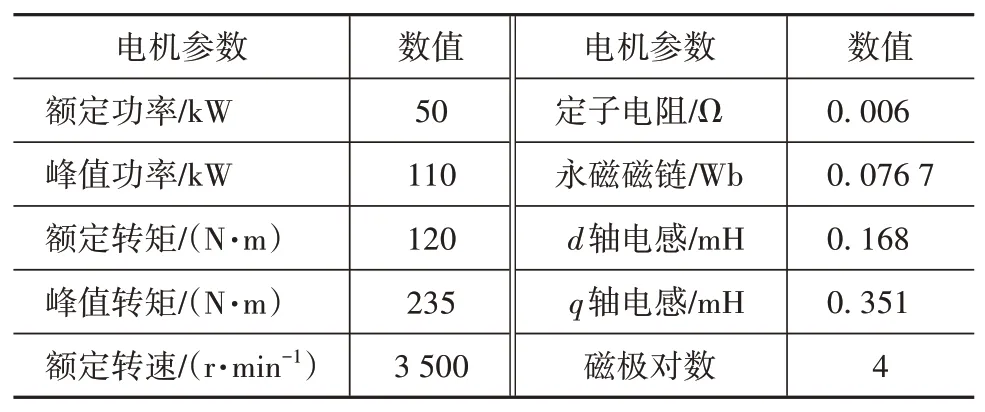
表1 试验用永磁同步电机参数

3.1 电流闭环控制仿真

为验证本文提出的变权重叠加型过调制方法的控制效果，采用电流闭环控制进行仿真验证。电流环PI控制器的输出控制量加上前馈量得到参考电压v*d和v*q，再通过平方和求根方法得到参考电压矢量幅值|Vs|，由反正切函数得到参考电压矢量在两相旋转坐标系下的相位角θs_2r。θs_2r与传感器测得的转子位置角θm取和得到参考电压矢量在两相静止坐标系下的相位角θs_2s，为书写简便，将θs_2s简写为θs。在过调制方法模块中，幅值|Vs|用于计算调制系数MI，相位角θs用于计算叠加权重因子kopt。经过过调制方法模块得到的调制电压矢量分解为v*α和v*β，再通过SVPWM模块计算得到六路PWM信号对逆变器的功率开关器件进行控制。电流闭环控制仿真模型架构如图10所示。

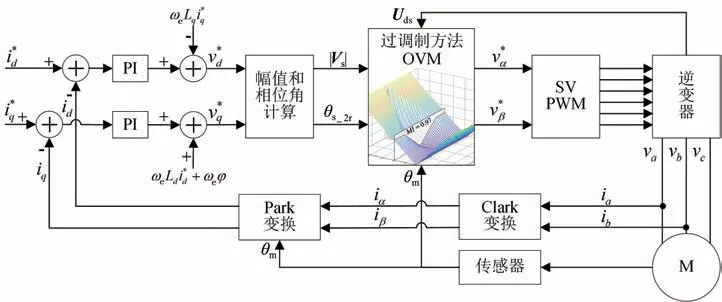
图10 仿真控制架构

在电机转速稳定至5 000 r∕min后进行目标电流阶跃测试，以验证消除电压突变是否能够提升驱动电机目标电流稳定性，减小电机输出转矩抖动。在8.05 s时刻，d轴电流目标值从0阶跃至-150 A，q轴电流目标值从0阶跃至250 A，结果如图11～图13所示。

图11对比了电流的稳定性。图11（a）为传统方法的dq轴电流图像，可以看出，传统方法电流稳定性较差，且稳态电流存在较大幅度抖动，电流抖动峰峰值PP_Id和PP_Iq分别为53.4和40.2 A。图11（b）为本文方法的dq轴电流图像。由图可见，电流稳定性得到了提升，且电流抖动幅值也相应减少，dq轴电流抖动峰峰值PP_Id和PP_Iq分别减小至34.9和17.5 A，峰峰值与有效值的比值相较于传统方法分别降低了12.3%和9.1%。

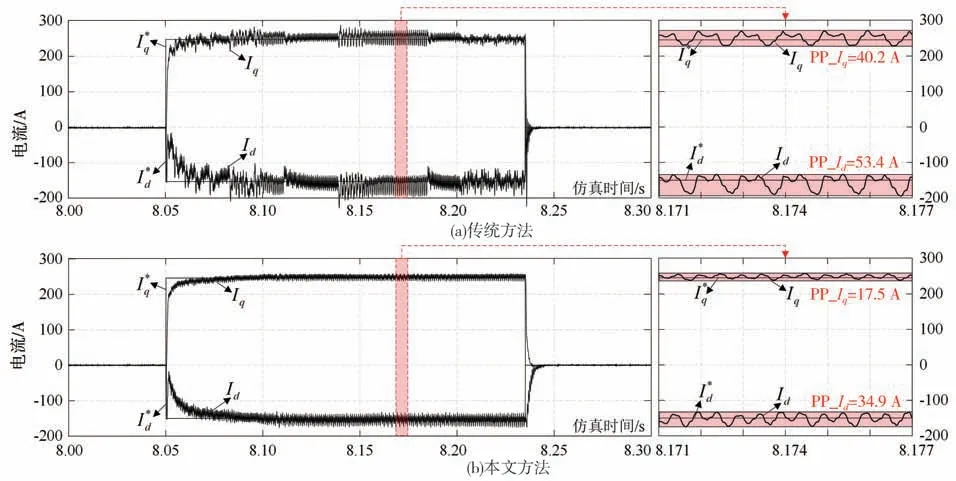
图11 电流稳定性对比

调制电压是FOC电流环输出的控制量，图12为相电压波形的对比。由图12（a）可见，传统方法中调制电压谐波畸变率偏高，THD=18.79%，这是造成dq轴电流抖动较大的主要原因；由图12（b）可见，本文提出的变权重叠加型过调制方法中调制电压变化更为平滑，使谐波畸变率THD降低至12.18%，dq轴电流的稳定性得到了提升，且电流抖动幅值也相应减小。

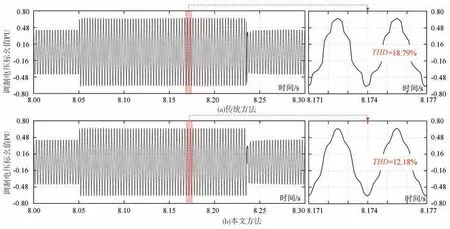
图12 相电压波形对比

永磁同步电机转矩公式为

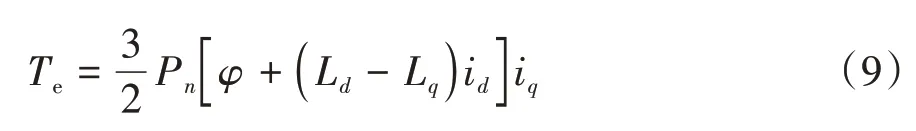
式中：Te为电机转矩；id、iq为d轴和q轴电流；Pn、φ、Ld、Lq分别为磁极对数、永磁磁链、d轴电感和q轴电感。

由式（9）可知，dq轴电流的抖动将会直接造成电机输出转矩的抖动，这从图13电机输出转矩的对比得到印证。由图13（a）可见，传统方法由于dq轴电流抖动幅度较大，所以电机输出转矩抖动峰峰值也偏大，达到20.7 N·m；由图13（b）可见，本文方法中的电机输出转矩抖动峰峰值减小至13.6 N·m，降低了34.3%。而峰峰值与有效值的比值也比传统方法减小了4.5%。

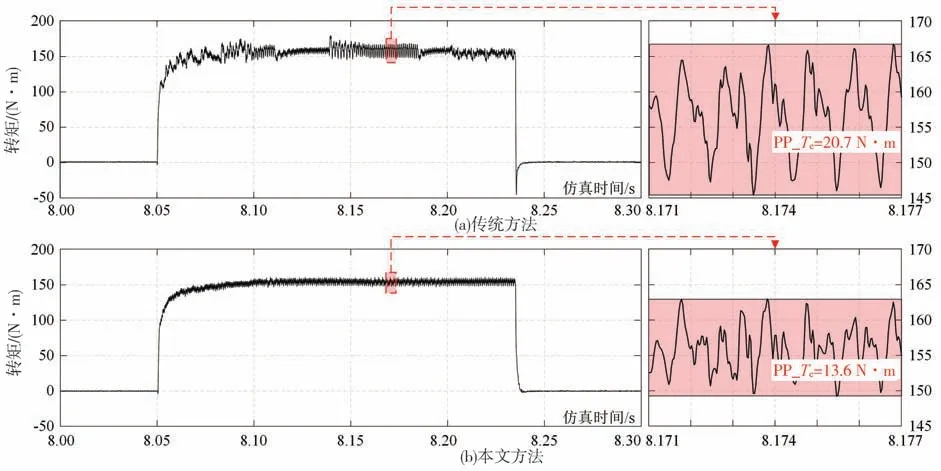
图13 电机输出转矩对比

图14为本文方法过渡阶段的极电压、相电压标幺值和相电流波形。电机转速为5 000 r∕min，保持Id不变，通过增加Iq来提高调制系数，使电机控制器从过调制Ⅰ区过渡到过调制Ⅱ区，最终过渡到六拍阶梯波工况。当8.575 s≤t＜8.585 s时，电机控制器工作在过调制Ⅰ区，极电压、相电压和相电流波形出现畸变；当8.585 s≤t＜8.600 s时，电机控制器工作在过调制Ⅱ区，极电压、相电压和相电流波形畸变更为明显，但相电压没有出现突变现象；当t≥8.600 s时，电机进入六拍阶梯波工况，极电压、相电压和相电流波形连续，变化平滑，证明本文方法能够实现过调制Ⅰ区、过调制Ⅱ区和六拍阶梯波工况之间的平滑过渡。

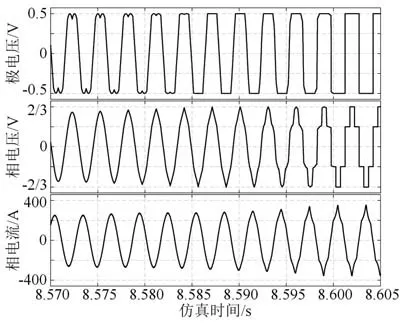
图14 过渡阶段波形

图15示出调制系数MI分别等于0.951 7、0.96、0.97、0.98、0.99、1.00时叠加权重因子kopt的变化曲线。可以看出，叠加权重因子能够在电压调制六边形任意扇区的中心位置从初始值逐渐减小至0，消除此时叠加分量发生跳变带来的影响，解决了调制电压在过调制Ⅱ区存在的突变问题。同时，在调制系数MI分别为0.951 7和1.00时，叠加权重因子分别保持0和1.0不变，结合式（8），从侧面确保了该方法的过渡平顺性。

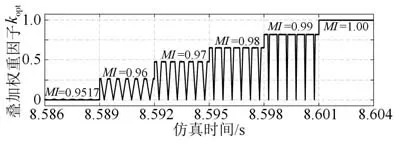
图15 叠加权重因子

3.2 台架试验验证

台架试验在永磁同步电机拖动试验台架上进行，主要包括被测电机及控制系统、拖动电机与控制系统和功率分析系统。试验台架如图16所示。被测电机控制系统由本实验室自主开发，采用模型开发直接生成控制代码。被测电机为某款电动公交车实际搭载的永磁同步驱动电机，主要参数如表1所示。

图16 电机拖动试验台架

选 取 调 制 系 数MI=0.97、0.98、0.99与 传 统SVPWM线性调制区边界值MI=0.9069进行对比验证。在拖动电机将转速稳定至5 000 r∕min后，保持目标转矩等于155 N·m不变，即电机输出功率保持不变，通过调整调制系数进行试验，结果如图17所示。由图可见，随调制系数的增加，线电压波形直接导通的时间占比增大，意味着电压利用率增加，与传统SVPWM的线性调制区相比，动力电池母线电压利用率提升了9.2%，电机绕组电流有效值减小了8.4%，电机的热损耗理论上能够降低16.3%。随调制系数的增加，电机输出转矩的抖动也在增大，但抖动幅值都在±6.5%以内。

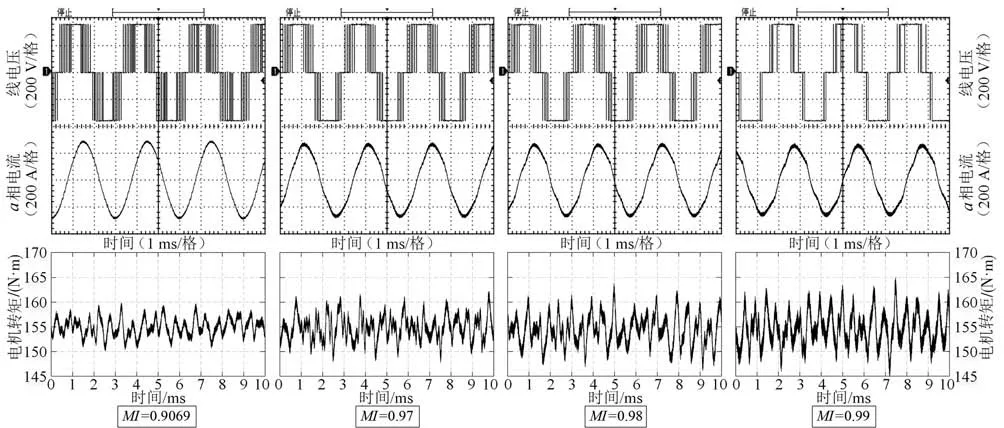
图17 实测线电压、相电流和电机转矩波形

本文中提出的过调制控制方法与传统SVPWM线性调制控制方法的电机外特性曲线对比如图18所示。可以明显看出，应用过调制方法拓宽了电机外特性曲线范围，提升了高转速区域电机转速调节能力和转矩输出能力。运用传统SVPWM线性调制控制方法，电机最大转速为8 000 r∕min，运用本文过调制控制方法，电机最大转速提升至8 819 r∕min，提升幅度为10.2%。转矩输出能力的提升以转速为6 000 r∕min为例，如图19所示。运用传统SVPWM线性调制控制方法时，电压利用率被限制在MI=0.9069以内，所以当目标转矩超过182.2 N·m后，电压利用率达到饱和状态，输出转矩不再增加，此时电机输出功率为114.9 kW。运用本文过调制方法时，电压利用率可达到MI=1.00，电机最大输出转矩提升至196.4 N·m，输出功率提升至123.4 kW，提升幅度为7.8%。可见，采用本文过调制方法有效提高了电动汽车驱动电机的最大转速、转矩和输出功率。

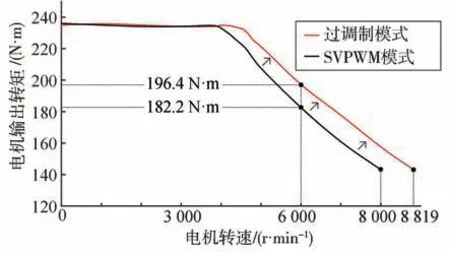
图18 外特性曲线对比

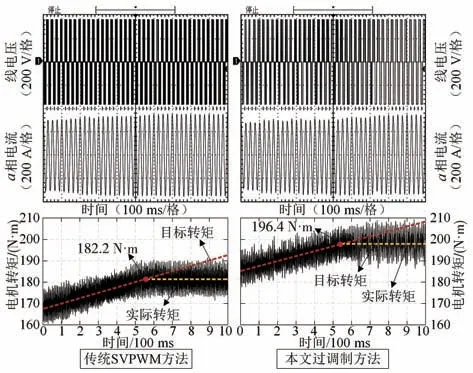
图19 6 000 r∕min时电机最大输出转矩对比

4 结论

提出一种变权重叠加型过调制方法，能够在提高电动汽车转矩输出能力和转速调节能力的同时，保证动力输出的稳定性和平顺性。

该方法将参考电压的相位角引入叠加权重因子计算，消除了加权分量跳变对调制电压的影响，解决了传统过调制方法在过调制Ⅱ区出现的调制电压突变的问题。仿真与试验表明：与传统过调制方法相比，本文方法消除了调制电压在过调制Ⅱ区出现的突变，降低了谐波畸变率，因此提升了dq电流稳定性，降低了电机输出转矩的抖动，使电动汽车动力输出更加稳定和平顺；与SVPWM线性调制方法相比，本文方法拓宽了电机外特性曲线范围，在高转速区域内提高了电机输出的最大转矩和最大转速，增强了驱动电机转矩输出能力和转速调节能力，提升了整车动力输出性能。