考虑驾驶权动态分配的共享转向系统鲁棒控制*

李学鋆，汪怡平，苏楚奇，宫新乐，黄 晋，刘 珣，袁晓红，李惠乾

（1.武汉理工大学，现代汽车零部件技术湖北省重点实验室，武汉 430070；2.武汉理工大学，汽车零部件技术湖北省协同创新中心，武汉 430070；3.清华大学车辆与运载学院，北京 100084）

前言

当前，由于自动驾驶技术还不够成熟、人-车权责划分不明确［1］、驾驶员对驾驶权迅速转换的适应性较差［2］以及很多人将驾驶作为个人爱好［3］等，很多驾驶场景仍需要驾驶员参与决策与控制。另一方面，即使在自动驾驶过程中，驾驶员仍然需要保持实时在环，以保证在危险时刻具备良好的反应能力［4-5］。作为智能驾驶的技术之一，人机共驾（human machine co-driving，HMC）系统是解决人机协同控制的有效方案。

共享转向控制（shared steering control，SSC）是一种常用的HMC控制方法，它是由“人-控制器-车-环境”组成的双闭环控制系统。SSC系统通过对驾驶员和自动驾驶系统的驾驶权动态分配，实现人车协同控制［6］，已被用于车道保持［7］、大曲率路径跟踪［8］、换道［9］和避障［10］等场景。SSC系统的研究主要包括：驾驶权分配方法和控制算法。驾驶员和自动驾驶系统的驾驶权动态分配和稳定转换可以保证SSC系统的可靠性和有效性［11］，尤其是在复杂行驶工况下，如干扰、驾驶员误操作等。开发与SSC系统匹配的控制算法可以提高SSC系统的鲁棒性和控制精度。

Saleh等［12］提出了一种驾驶权分配系数固定的SSC系统，用于削弱驾驶员不确定行为的影响。Wang等［13］提出了一种基于指数函数的驾驶权分配函数，结合前馈控制方法提高车辆的轨迹跟踪能力。刘瑞等［14］提出了基于非合作模型预测控制的人机共驾控制策略，实现驾驶员和控制系统之间驾驶权的平滑交接。Sentouh等［15］提出了一种基于指数函数的驾驶权分配函数，并设计了反馈鲁棒控制器实现了车道保持辅助系统与驾驶员之间的驾驶权转换，提高了车道线保持能力。谢有浩等［16］提出了基于μ综合方法的人机共驾鲁棒控制器，用于减小驾驶员误操作的影响。Li等［17］针对人机共驾系统中的驾驶安全和人机冲突问题，提出了一种考虑驾驶员驾驶特性和状态的驾驶权分配模型，提高了系统的抗干扰性能。Nguyen等［18-19］利用U形函数设计了考虑车辆运行状态和驾驶员驾驶状态的驾驶权分配模型，并基于模糊理论设计了考虑参数不确定性的鲁棒控制器。为了提高大曲率路径跟踪的精度，同时考虑驾驶员行为的不确定性，Wang等［8］提出了一种基于模糊策略的驾驶权分配方法，并设计了模糊动态补偿控制器。郭烈等［20］利用模糊控制器实现了驾驶员与车道保持辅助控制系统之间的驾驶权动态分配，结合MPC-PID串级控制方法，提高了车道保持辅助系统的可靠性，同时可以降低人机冲突。以上研究针对特定应用场景或目标提出了驾驶权分配方法，并通过设计合理的控制器有效地提高系统的可靠性和车辆行驶安全。

但在这些研究中存在两个问题：

（1）驾驶员和自动驾驶系统的驾驶权系数之和通常被设为1。而实际上，如果驾驶员和自动驾驶系统的驾驶权重之和设置为1或固定不变，在极限情况下，由于控制器输出饱和导致SSC系统的输出量与车辆保证行驶安全所需的控制输入量不匹配，从而使系统可靠性降低，影响车辆安全。

（2）由于SSC系统是“人-车-环境”和“控制器-车-环境”的双闭环控制回路耦合系统，驾驶权的动态分配会影响系统的控制精度，特别是大幅度变化可能会影响系统的稳定性。因此需要设计合理的鲁棒控制器削弱驾驶权分配系数动态变化对控制性能的影响。

为了解决因驾驶员和自动驾驶系统的驾驶权重之和被约束导致SSC系统控制精度下降问题，提高系统的稳定性和可靠性，本文提出了一种驾驶权动态分配方法，并在此基础上设计了考虑车辆模型参数和驾驶权分配系数不确定性的鲁棒控制器。仿真结果验证了所提出的SSC系统的有效性。

1 SSC系统模型

1.1 车辆轨迹跟踪模型

为了反映车辆在轨迹跟踪过程中与参考轨迹之间的相对位置关系，建立如图1所示的车辆轨迹跟踪模型。定义局部坐标系xoy和惯性坐标系XOY，车辆在跟踪预定轨迹时会产生航向角误差eφ和横向位置误差ey。

图1 车辆轨迹跟踪模型

航向角误差为车辆航向角与理想航向角之间的差值：eφ=φ-φd。一般，期望航向角速度φ̇d可以表示为期望路径曲率ρ与纵向速度vx的乘积：φ̇d≈vx ρ。eφ的1阶导数可以表示为

车辆的横向位置误差ey的1阶导数为

式中vy为车辆的侧向速度。

轨迹跟踪过程中，航向角误差一般较小，考虑建模和传感器测量误差，ėy和ėφ可进一步表示为

式中d1和d2分别为数学建模和传感器测量引起的误差。

1.2 车辆侧向动力学模型

本文提出的SSC系统基于如图2所示的2自由度车辆模型，其动力学方程为

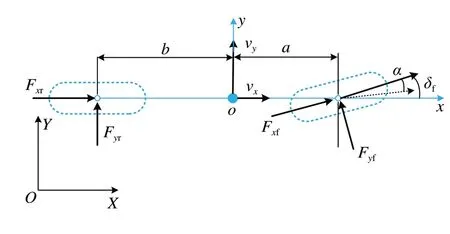
图2 2自由度车辆模型

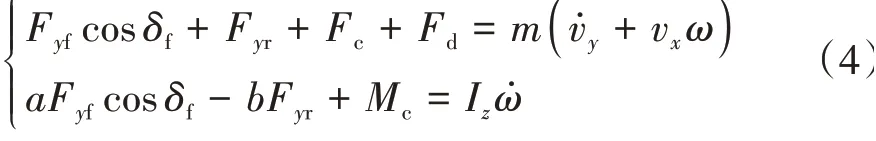
式中：δf为前轮转角；Fyf和Fyr分别为前后轮的侧偏力；ω为横摆角速度，其大小与φ̇相近似；Iz为绕z轴的转动惯量；Fc为侧风引起的侧向力；Fd为外部其他干扰力；Mc为侧风引起的横摆力矩。

侧偏力可以表示为

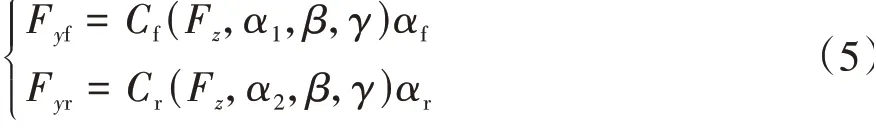
式中：αf和αr分别为前后轮侧偏角；Cf(Fz，αf，β，γ)和Cr(Fz，αr，β，γ)分别为前后轮侧偏刚度，它们与垂直载荷Fz、侧偏角αi、车辆质心侧偏角β以及车轮前束角γ有关［21］。前后轮侧偏角可近似表示为

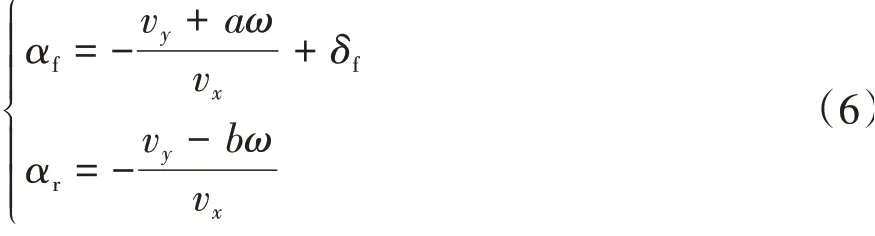
式中a、b分别为车辆质心到前、后轴的距离。

将式（5）和式（6）代入式（4），由于δf较小，cosδf≈1，可以得到：

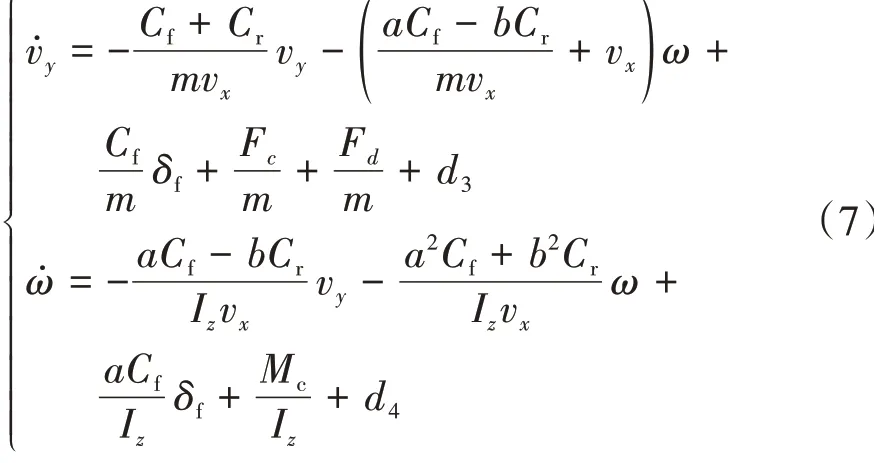
式中d3和d4为数学建模引起的误差。

转向系统的数学模型可以简化为2阶模型［22］：

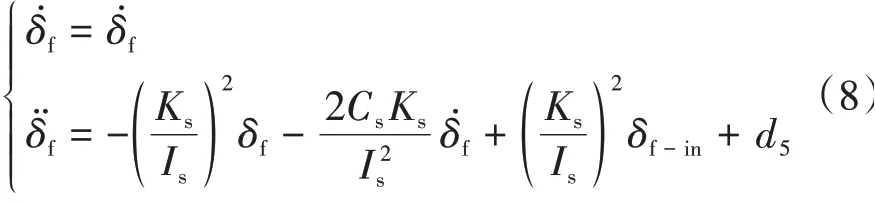
式中：Is、Ks、Cs分别为转向系统的惯性、刚度和阻尼系数；δf-in为控制输入；d5为建模误差。

综合式（3）、式（7）和式（8），可以得到：

为系统干扰，建立模型的状态空间方程：

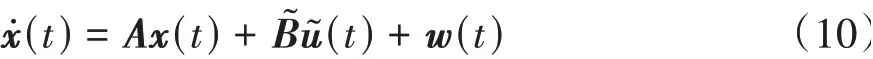
其中：

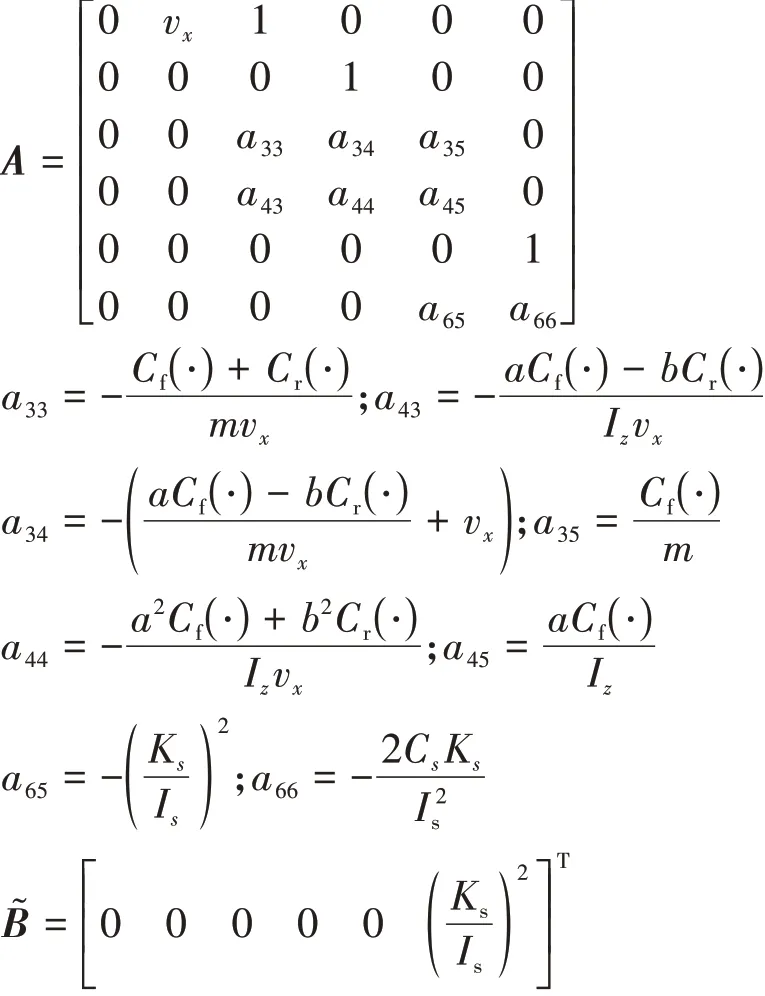
对于SSC系统，车辆的输入由两部分组成：驾驶员输入的有效转角k1δd和控制器的有效输入转角k2δd，k1和k2为驾驶权分配系数。式（10）可改写为

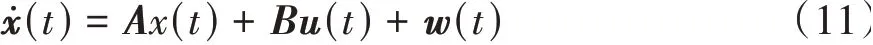
其中

1.3 驾驶员模型

驾驶员模型是SSC系统中的关键性环节，需满足：（1）模型能够描述驾驶员预瞄行为和驾驶特性；（2）具备驾驶员的适应性特性。驾驶员在跟踪路径曲率过程中，通常以道路内侧边界和道路中心线作为参考。双点预瞄驾驶员模型能较好地描述该过程中的驾驶行为。双点预瞄驾驶员模型［23］如下：

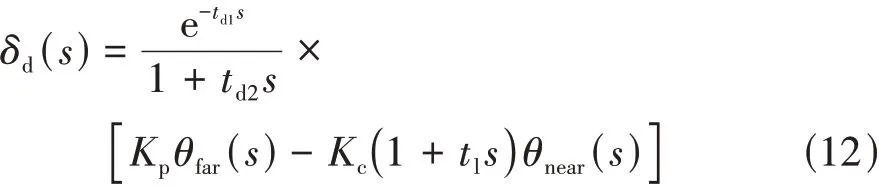
式中：td1和td2分别表示驾驶员大脑反应时间和手臂肌肉反应时间；θfar≈lfarρ，lfar为驾驶员距道路边界预瞄 点 的 距 离，lfar=tpvx，ρ为 路 径 曲 率；为驾驶员距道路中心线预瞄点的距离，lnear=0.4lfar；Kp和Kc为两个增益系数。利用式（12）可以得到驾驶员模型空间方程：

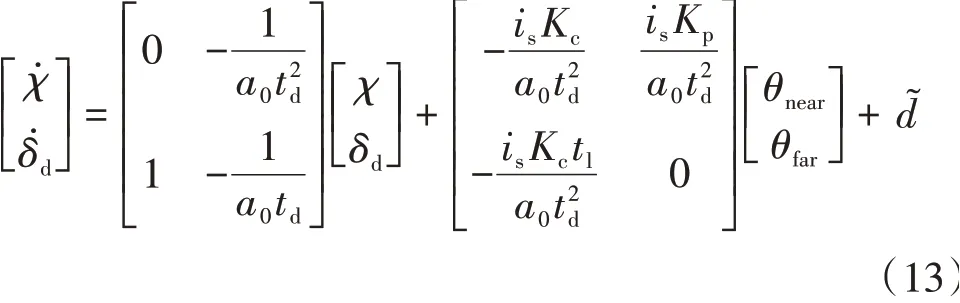
Wang等［23］通过仿真与实验给出了参数td、tp、tl、Kp、Kc的 取 值 范 围 分 别 为：td∈(0.12，0.30)，tp∈(1.00，2.00)，tl∈(0.18，0.19)，Kp∈(1.00，4.00)，Kc∈(0.80，3.50)。

2 驾驶权动态分配模型

2.1 SSC系统框架

SSC系统是“人-控制器-车-路”构成的双闭环耦合系统，可以根据驾驶员行为和车辆运行状态，通过驾驶权分配模型合理分配驾驶权重，协调驾驶员与自动驾驶控制器的关系，弱化系统内部和外部不确定因素的干扰。SSC系统框架包括串联式和并联式。本文在并联式SSC系统框架的基础上进行拓展，提出了如图3所示的SSC控制框架。系统控制框架包括两部分：驾驶权动态决策和SSC控制。

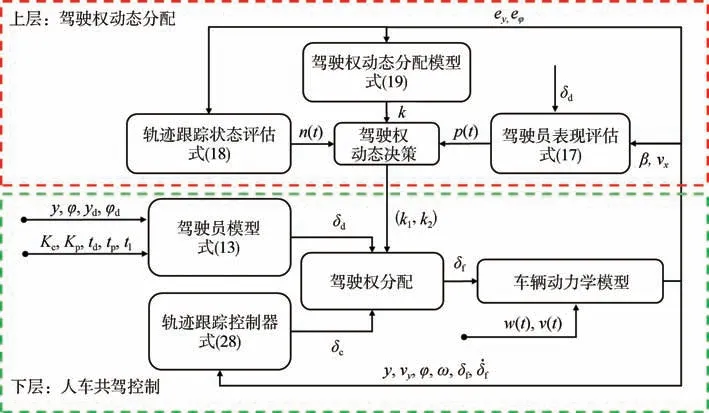
图3 SSC控制框架

驾驶权动态决策包括驾驶权分配与决策。驾驶权分配模型用于计算驾驶员的理想驾驶权分配系数k。驾驶权决策依据包括驾驶员状态评估和车辆轨迹跟踪状态评估。基于决策依据和驾驶权限分配模型计算得到的结果k，可以对驾驶员驾驶和控制器的驾驶权分配系数进行动态决策。根据决策结果可以得到车辆的前轮转角δf=k1δd+k2δc，δf用于控制车辆完成轨迹跟踪任务。

2.2 驾驶权动态决策依据

驾驶车辆的过程中，驾驶员根据路径不断调整预瞄位置，并调整到达预瞄位置的转向盘转角，从而完成轨迹跟踪。根据预瞄点位置和车辆运动学得到驾驶员的理想转角［24］：

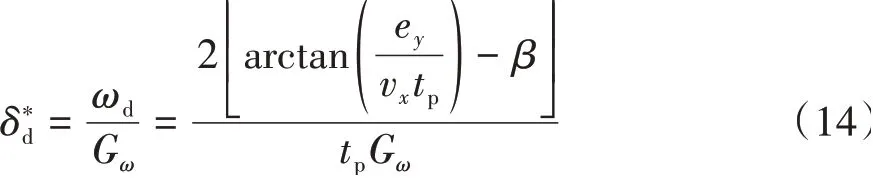
此外，为了保证行驶安全，须考虑路面附着：

如图4所示，驾驶员预瞄点（Pl和Pr）的极限位置位于道路的安全边界上。车辆到达Pl和Pr所需的理想车辆转角为θl和θr。

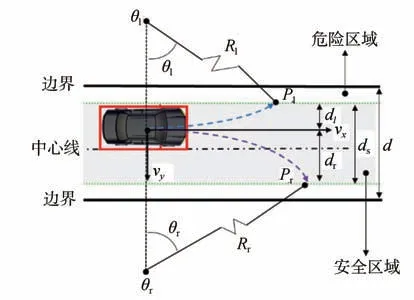
图4 安全边界计算示意图

根据式（14）、式（15）和图（4），计算得到驾驶员转向盘转角的安全边界：

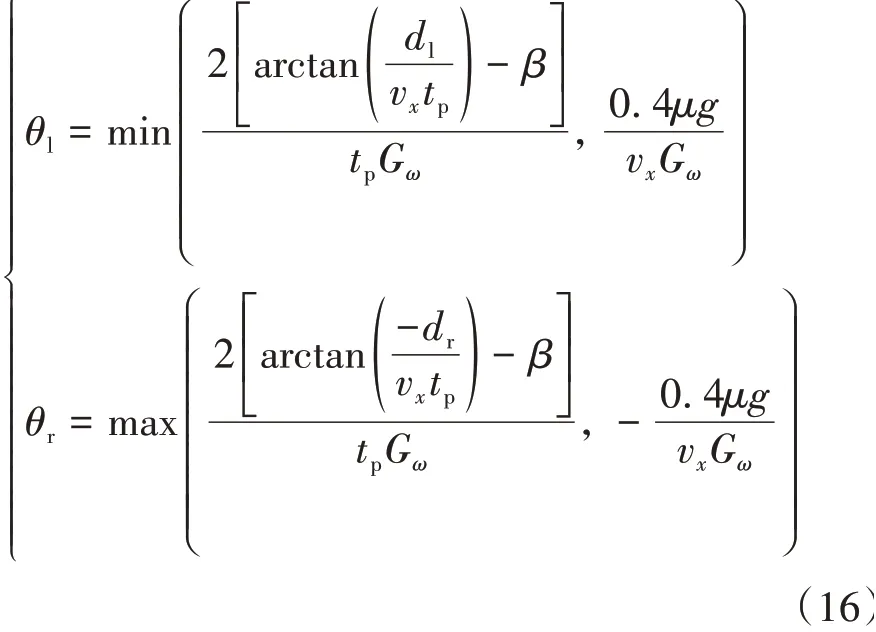
式（16）是关于dr(df)、vx、tp、β的函数，dr(df)、vx、β为车辆的状态参数，tp与驾驶员驾驶特性有关。不同的车辆状态和驾驶员状态所确定的驾驶员输入转角安全阈值也会发生变化，即，驾驶员的转向盘转角须满足：θr≤δd≤θl

建立驾驶员表现评估函数：式中：pmin为驾驶员表现评估结果的最小值，防止因建模误差、驾驶员不同驾驶特性等因素导致估算值过低问题，本文取0.2；λ1和λ2为常数，用于调整p(δd)的变化速度，均取0.5；λ3为常数，取5。

基于侧向位移误差建立车辆轨迹跟踪状态评估函数：

式中ζ为正常数，其大小可以通过标定点计算得到，本文取10。

2.3 驾驶权动态分配与决策

根据驾驶员的驾驶状态和车辆状态动态调整驾驶权，可有效降低人机冲突，提高抗干扰能力［17］。在驾驶权动态分配模型中常将驾驶员输入［18］、侧向位移误差［25］、航向角误差［26］、驾驶员的驾驶特性等作为函数变量［17］。综合考虑侧向位移误差（ey）和航向角误差（eφ）的影响并设计驾驶权分配模型：

在极限工况下（侧风、冰雪路面）或驾驶员误操作时，由于控制器输出约束或执行器速率约束，k1+k2=1的驾驶权分配方式影响控制效果，甚至出现危险。为了解决这一问题，在驾驶权分配模型的基础上设计基于驾驶员转向操作状态评估和车辆轨迹跟踪评估的驾驶权决策策略，将车辆当前的风险评估结果和驾驶员输入转角安全域作为驾驶权分配的依据，对驾驶员和控制器的驾驶权进行动态调整。当车辆轨迹跟踪状态评估结果与驾驶员转向操作状态评估结果不符合控制要求时，k1+k2≠1。

驾驶权决策过程如表1所示。

表1 驾驶权决策过程

如果车辆轨迹跟踪状态评估结果n(t)超过阈值nˉ，并且驾驶员转向操作状态评估结果p(δd)超过阈值pˉ时，驾驶权分配可以采用k1=0.2、k2=1的分配策略，此时驾驶员的驾驶权限被严格控制（k1=0.2），且控制器被赋予最高等级的驾驶权限（k2=1）。在此过程中驾驶员的驾驶权只被削弱，但仍保留一部分驾驶权，这是为了保证驾驶员实时在环，提高驾驶员在紧急情况下的反应速度［3，27-28］。

决策过程中可能因驾驶权分配系数突变（k2→1，k1→0.2）而影响系统稳定性，因此在决策结果后加入1阶滞后环节。

3 鲁棒控制器设计

3.1 参数不确定性描述

当轮胎处于线性区域时，轮胎的侧偏刚度Cf，r(Fz，αf，β，γ)近似为常数，记为Cf0和Cr0。在复杂的环境下（侧风、冰雪路面）或车辆属性（质量、轮胎胎压）发生变化时，轮胎侧偏刚度很容易进入非线性区域。当轮胎进入非线性区域时，轮胎的侧偏刚度不再是常数，而成为随着Fz、αf，r、β、γ变化的复杂非线性函数，这使得所建数学模型（11）不再是线性模型，影响控制性能。为了解决这一问题，对Cf，r(Fz，αf，β，γ)的不确定性进行描述［22］：

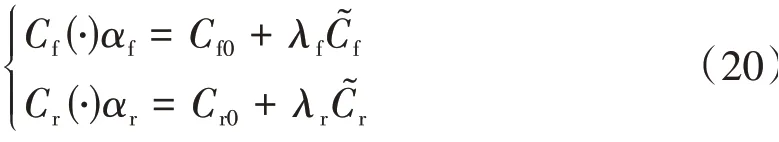
根据式（20），式（11）可被分解为［29］

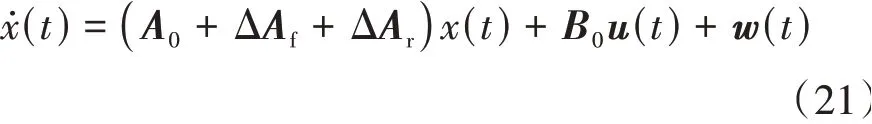
其中：

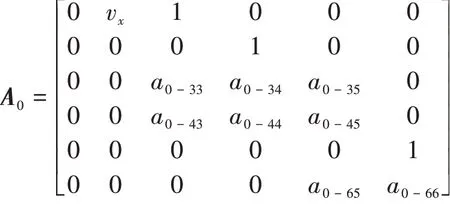
建立式（11）的过程中，车辆的纵向速度vx通常假设保持不变，使得系数矩阵保持为定常数矩阵。但事实上，由于路径曲率的变化、车辆转向以及侧风等环境影响，vx几乎不可能保持为一个常数。假 设和k可以分别表示为

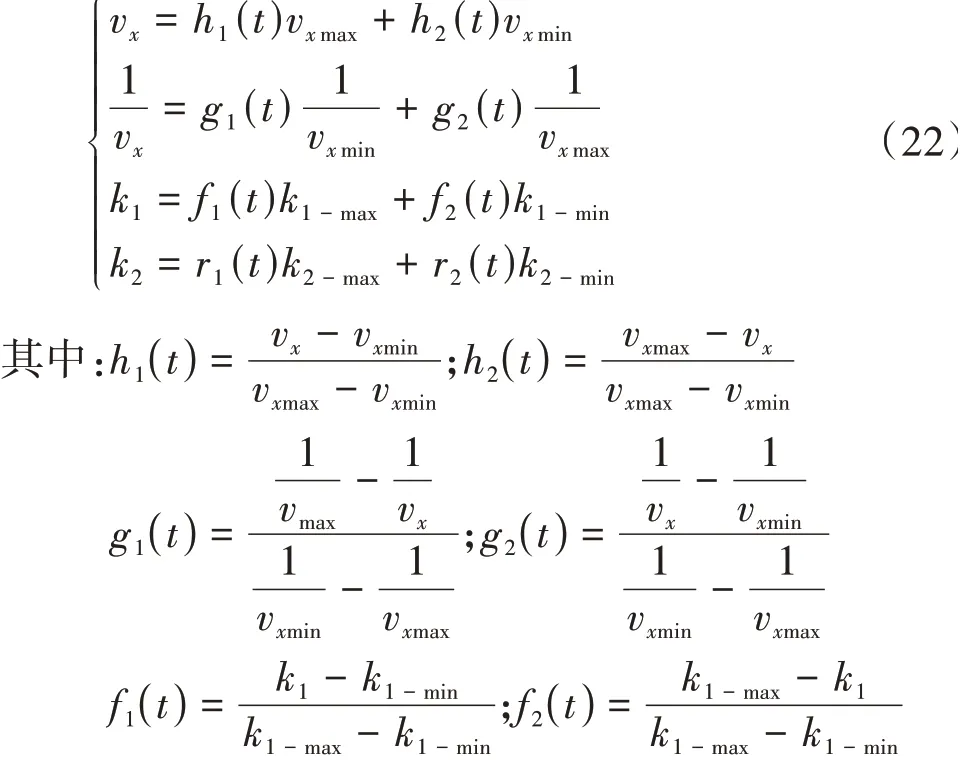
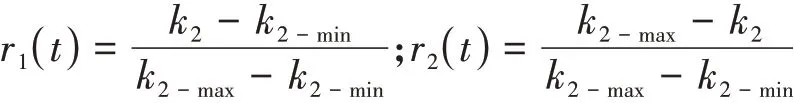
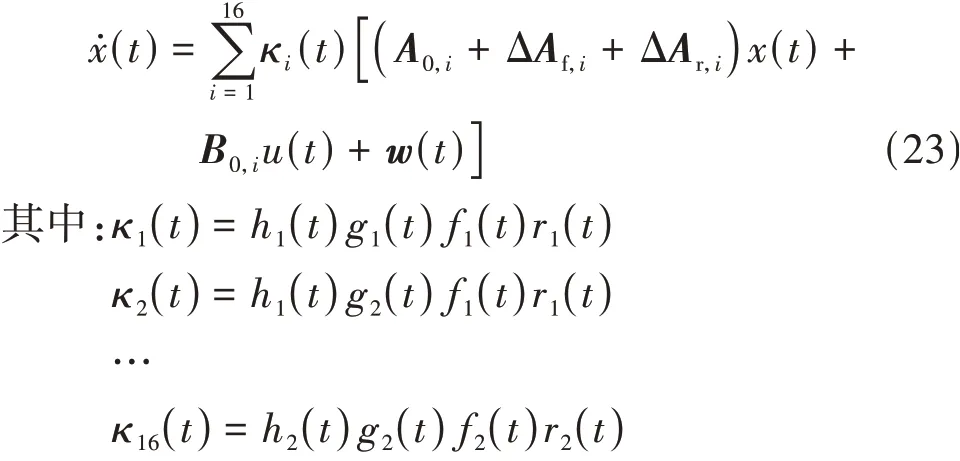
此时，考虑参数不确定性的车辆动力学模型为κi(t)满足两个条件：κi(t)≥0且A0，i、ΔAf，i、ΔAr，i、B0，i可以通过将A0、ΔAf、ΔAr、B0中的k2-min、k2-max。考虑不确定性因素的闭环系统模型可以写为

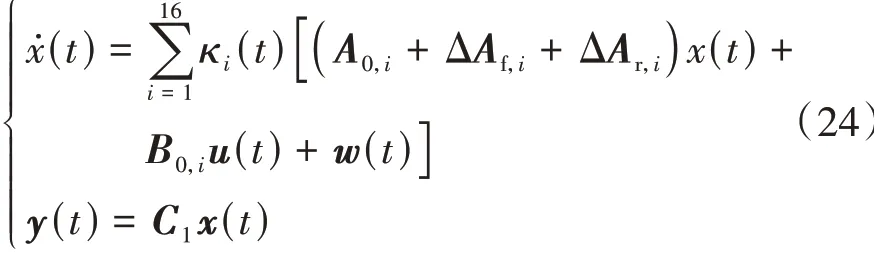
式中C1为6×6的单位矩阵。

3.2 鲁棒控制器设计

通过控制器实时得到最优的u(t)，控制车辆在轨迹跟踪过程中最大可能地降低ey和eφ，保证车辆的轨迹跟踪能力。鲁棒控制器的最优控制量为

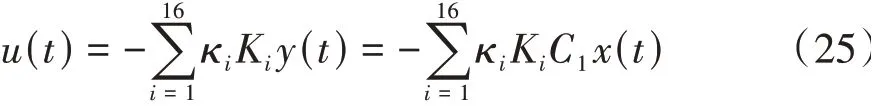
式中Ki为需要设计的控制增益量。

将式（25）代入式（24），得到闭环控制系统的数学模型：

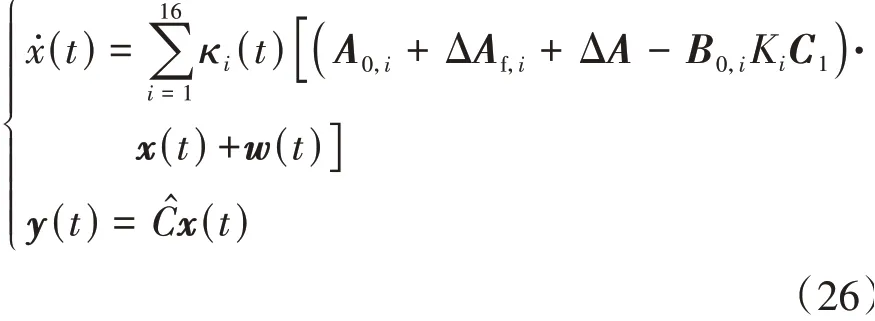
为了满足系统性能要求，引入性能指标函数Ξ(t)。在参数不确定性和外部扰动存在的情况下，通过寻找Ξ(t)的最小值，确定Ki。Ξ(t)可以表示为

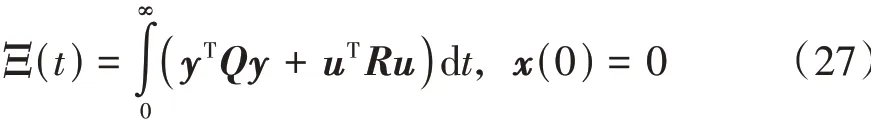
为了使式（26）系统可控且性能指标最优，提出以下准则定理1。

定理1.给定τ＞0，闭环控制系统在w(t)=0时保持稳定，且对于任意的w(t)≠0，w(t)∈[0，∞)满足式（27）H∞性能指标，需要满足：给定τ＞0，存在对称正定矩阵P，矩阵Ni使以下不等式成立：

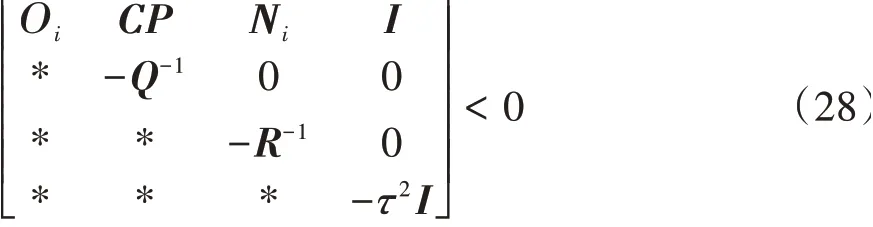
式中*表示对称矩阵中的对称元素。

式（25）定义的反馈增益Ki可以通过下式得到：

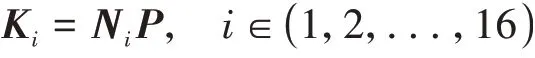
为了证明上述定理1，设计Lyapunov函数：

根据Schur补引理，式（28）可以转化为

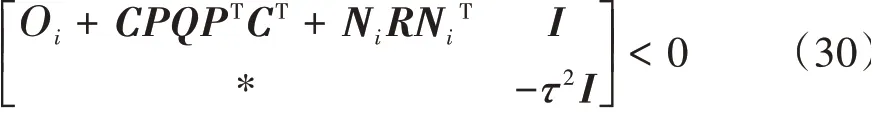
对式（30）左右同乘对角矩阵[P-1，I]，可得：

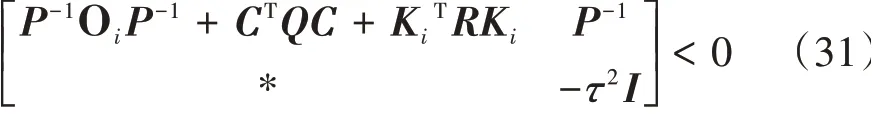
对式（31）左乘矢量[xT，wT]，右乘[x，ω]T，可得：

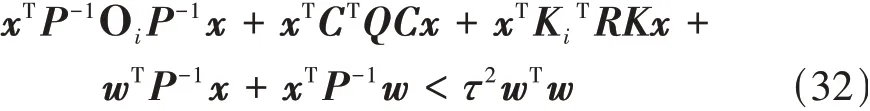
式（32）可以进一步化简为

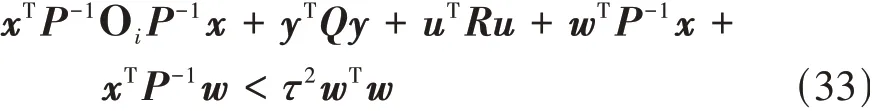
带入Lyapunov函数的1阶导数V̇(x)可得：

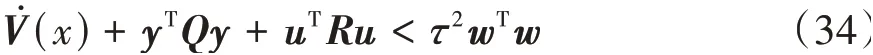
从式（34）可以看出，V̇(x)＜τ2wTw，即可以保证式（26）系统具备抗干扰能力。同样的，yTQy+uTRu＜τ2wTw，在初始条件x(0)=0时：

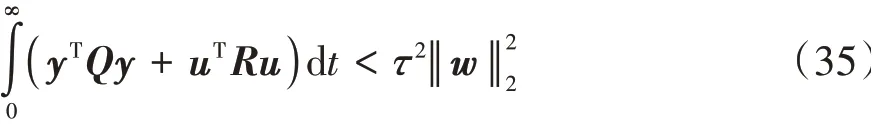
通过最小化τ，可以使Ξ(t)达到最优。定理1得证。利用LMI求解式（28）可得到最优控制量u(t)。

4 仿真与分析

为了验证轨迹跟踪控制器和人车驾驶权动态分配策略的有效性，本文设计了两个仿真场景，将所提出的SSC系统与驾驶权分配系数固定（k1=k2=0.5）的SSC系统进行对比。车辆参数如表2所示。

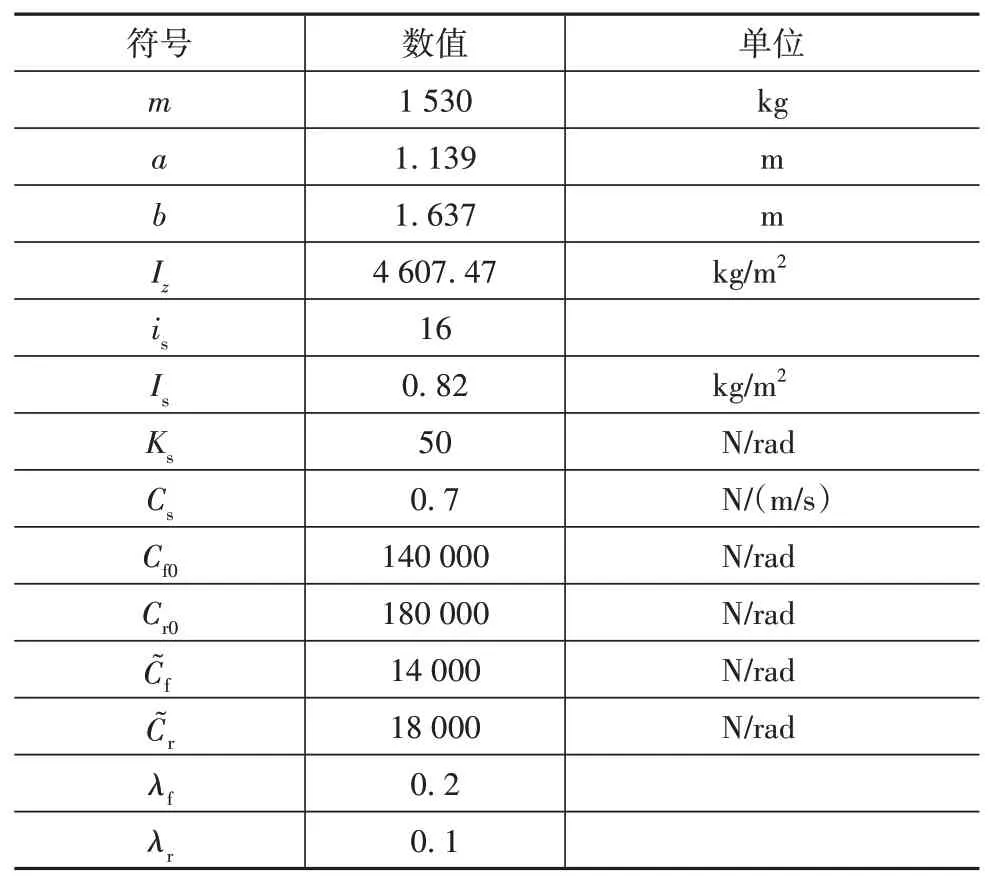
表2 仿真参数

4.1 仿真场景1

为了验证所设计系统对参数不确定性的鲁棒性，设置车辆换道仿真场景。道路附着系数为0.8，车速为v=20+5sin(20πt)km∕h，仿真时间为5 s。利用LQR控制器与鲁棒控制器进行对比，仿真结果如图5所示。

从图5可以看出，在车速高频率波动的情况下，LQR控制器不能很好地跟踪换道参考轨迹，在t=5 s时仍不能收敛，这是因为LQR控制器输出的前轮转角出现严重的转向不足；与此同时，LQR控制器输出的前轮转向角速度受到参数波动的影响出现高频波动，直接影响车辆的驾乘舒适性，而本文设计的鲁棒控制器可以很好地跟踪参考轨迹，且基本不受到参数波动的影响。说明本文设计的鲁棒控制器对参数不确定性具备良好的鲁棒性。

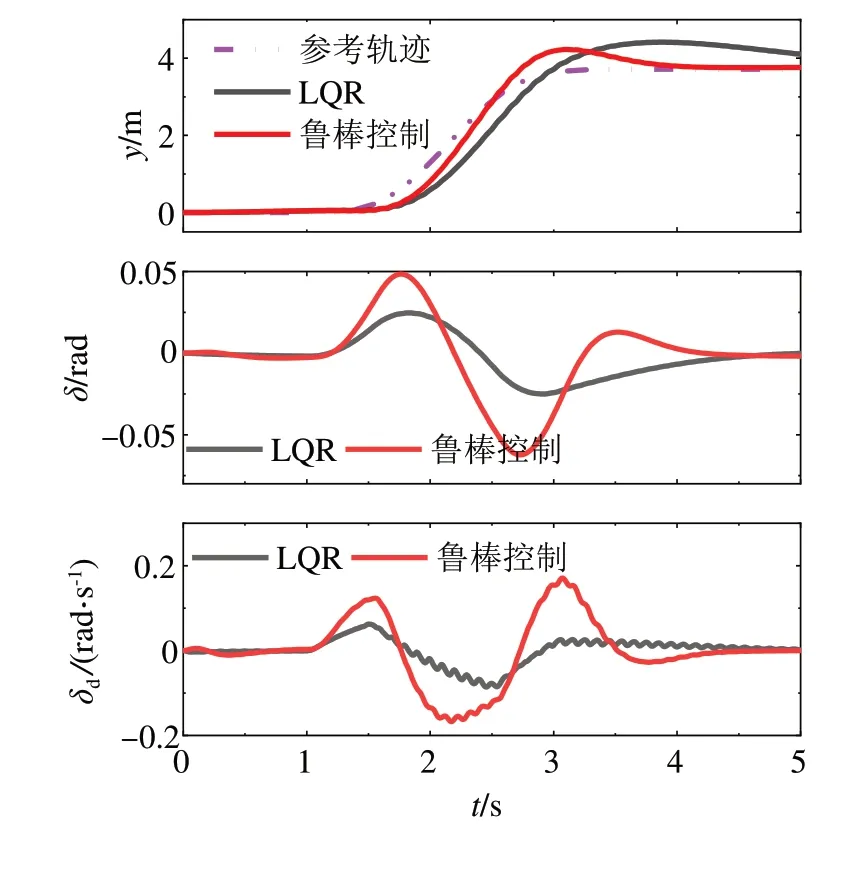
图5 换道场景下的侧向位移与转向参数曲线

4.2 仿真场景2

为了验证所设计系统的抗干扰性，设置车道线保持的仿真场景。道路附着系数为0.8，车速为v=20+2sin(πt)km∕h，仿真时间为10 s。仿真过程中车辆直线行驶，突然出现侧风（式（36）），且驾驶员出现误操作（3≤t＜4时，驾驶员输入为0）。

仿真结果如图6～图9所示，图6为车辆轨迹跟踪指标参数变化曲线，包括车辆侧向位移（y）和航向角（φ）；图7为车辆稳定性指标参数变化曲线，包括横摆角速度（ω）曲线和质心侧偏角（β）；图8为驾驶权动态决策结果（k1，k2）；图9为控制回路输出量，包括驾驶员输出量（δd）和控制器输出量（δc）。

从图6可以看出，驾驶员和SSC系统都可以使车辆在侧风环境下具备很好的轨迹跟踪能力。尽管驾驶员-车辆在最后没有因为误操作失去控制，但车辆的最大侧向位移误差和最大航向角误差分别达到了0.22 m，0.05 rad，远超过SSC。相对于驾驶员，SSC系统具备更好的抗干扰性，特别是当驾驶员误操作出现后，驾驶权分配系数固定的SSC系统和本文提出的SSC系统都可以保证车辆的轨迹跟踪能力。驾驶权分配系数固定的SSC系统也具备良好的抗干扰能力；且不一样的驾驶权分配系数会影响SSC系统的控制精度。相对于分配系数为k1=k2=0.5的SSC系统，非配系数为k1=0.4、k2=0.6的SSC系统的轨迹跟踪误差更小。相对于驾驶权分配系数固定的SSC系统，本文提出的SSC系统的J1相对于固定驾驶权分配方法（k1=k2=0.5）下降了6.67%，说明其具备更好的抗干扰性，也证明了所设计系统的有效性。

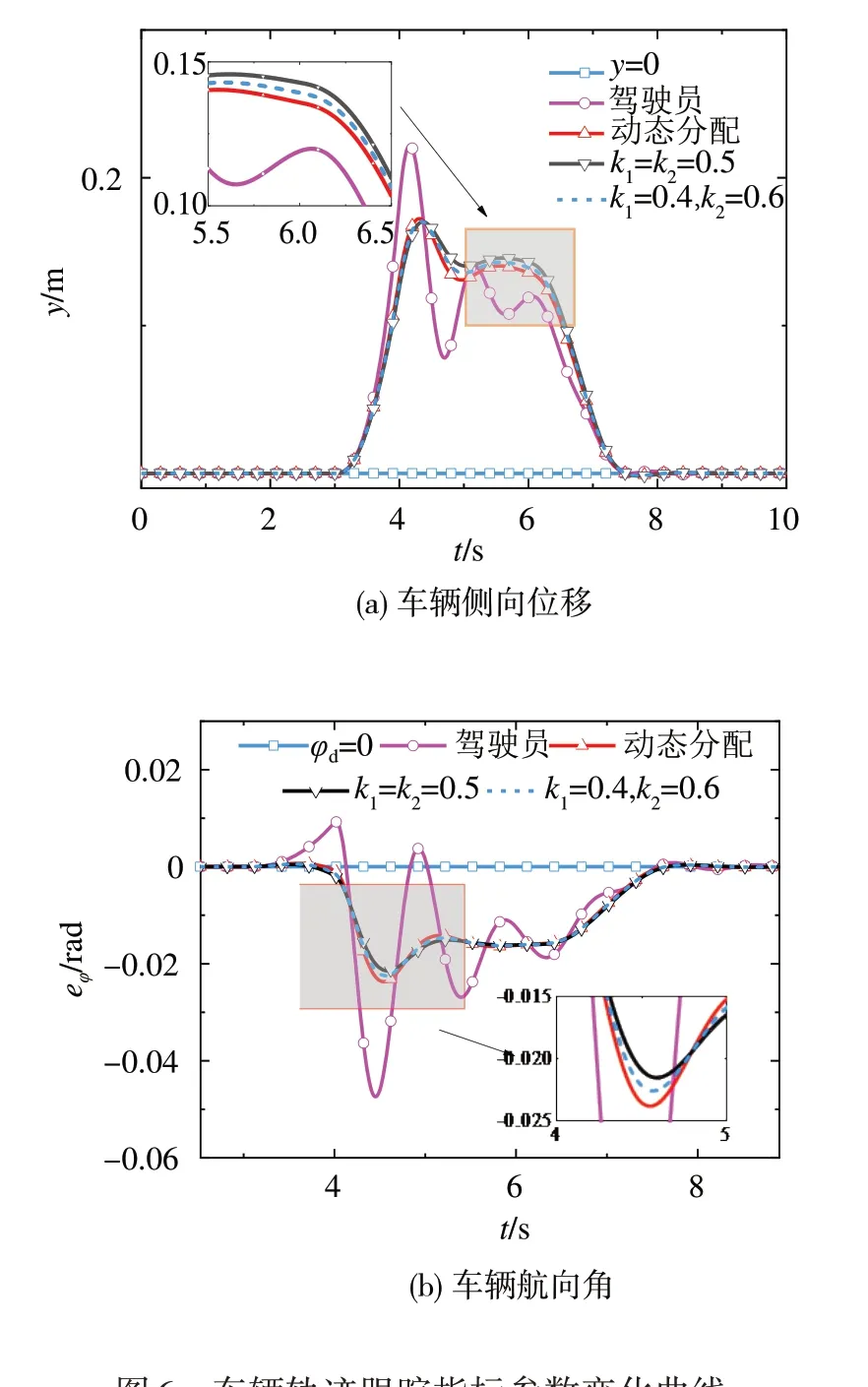
图6 车辆轨迹跟踪指标参数变化曲线

图7可以看出，在该仿真场景下驾驶员和SSC系统都可以保证车辆稳定行驶，但驾驶员的质心侧偏角和横摆角速度在误操作和侧风出现时波动幅度和波动频率明显变大。相对于驾驶员，SSC系统的横摆角速度可以更快收敛到0。说明本文所提出的方法具备良好的轨迹跟踪能力的同时，也能保证良好的行驶稳定性。

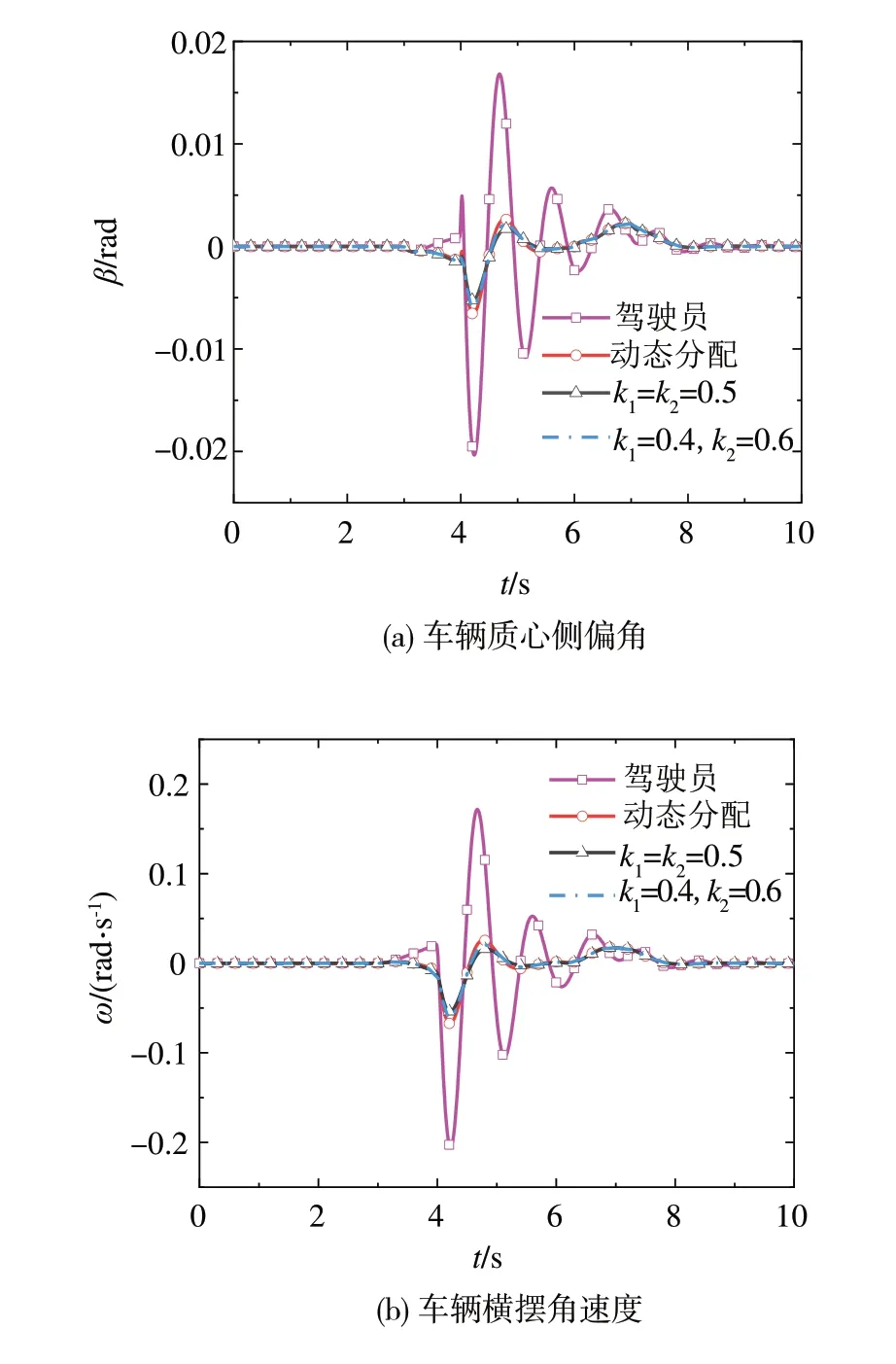
图7 车辆动力学响应

由图8可知，当驾驶员出现误操作后，驾驶员状态评估结果与车辆轨迹跟踪状态发生变化，导致动态决策结果出现变化。

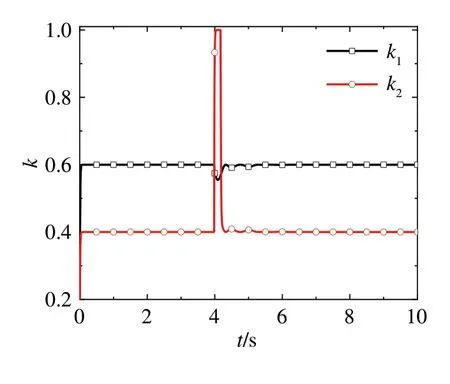
图8 驾驶权动态决策结果

从图9可以看出，当驾驶员出现误操作后，驾驶权分配系数固定的SSC系统和本文提出的方法都能迅速介入车辆控制，可以很好地抑制车辆进一步偏航。但相对于驾驶权分配系数固定的SSC系统，本文提出的方法的控制器输出量更大，配合驾驶权分配系数，车辆的侧向位移误差更小。

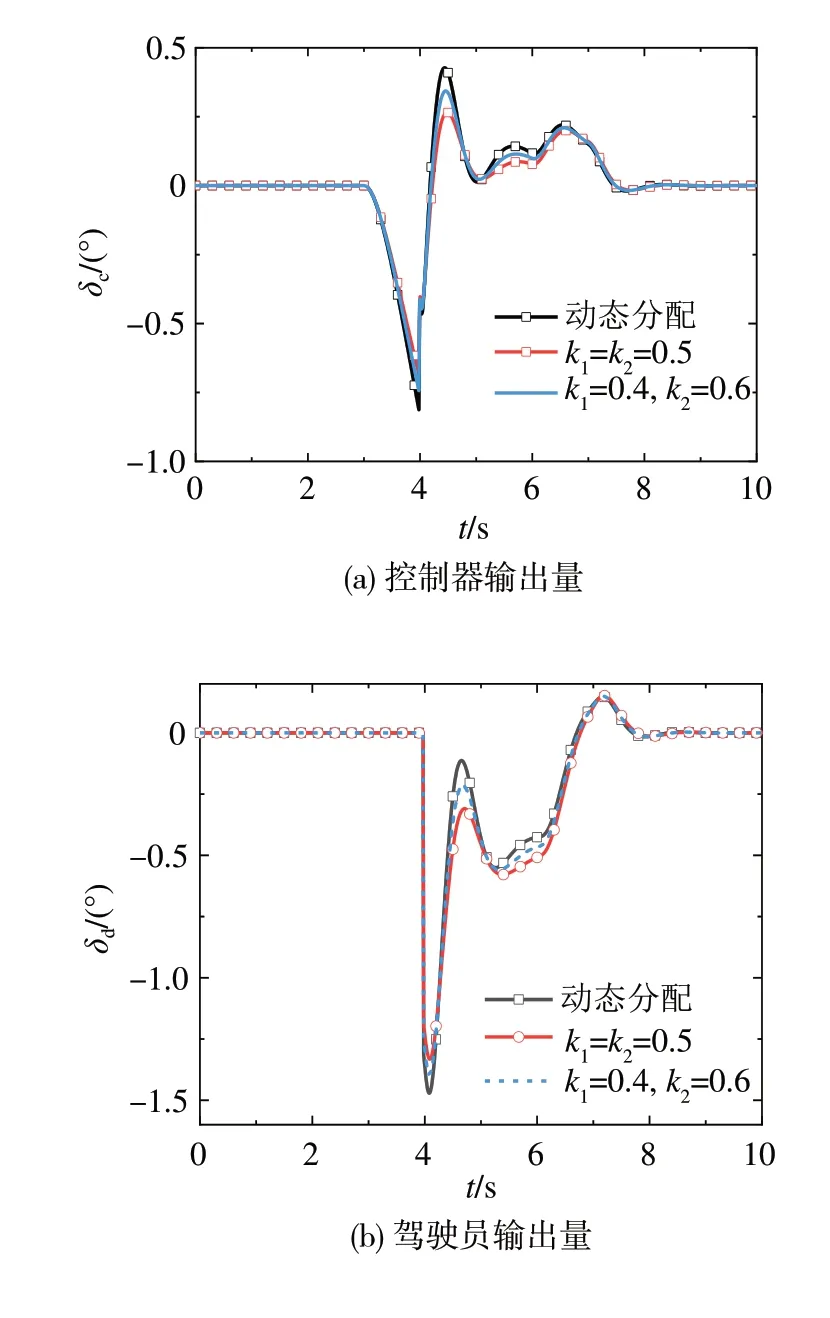
图9 双控制回路中的输出转角变化曲线

4.3 仿真场景3

为了进一步验证所设计SSC系统的抗干扰性和可靠性，设置车辆超车的仿真场景。仿真过程中车辆按照预定轨迹（见图10）行驶，超车过程中存在突发侧风（式（36）），车速为v=20+2sin(πt)km∕h，道路附着系数为0.8。

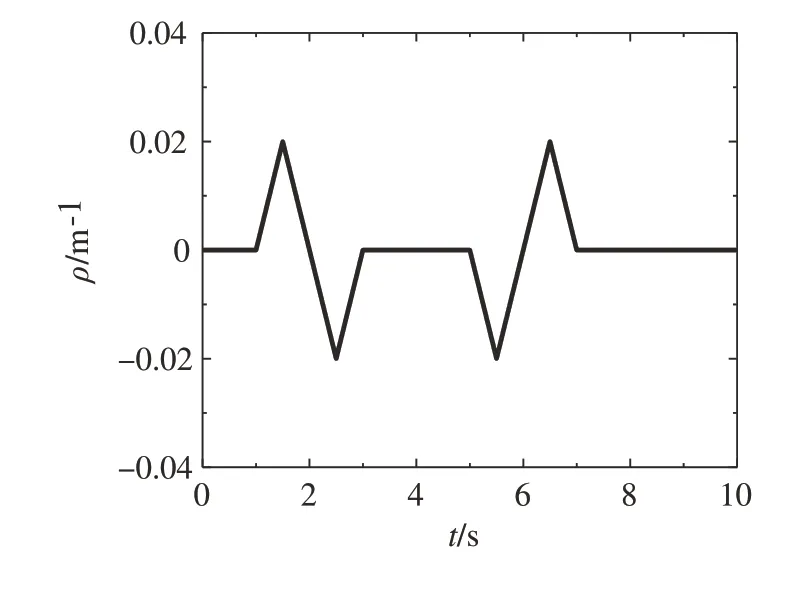
图10 车辆超车轨迹曲率

仿真结果如图11～图14所示。图11为车辆轨迹跟踪指标参数变化曲线，包括车辆侧向位移（y）和航向角（φ）；图12为车辆稳定性指标参数变化曲线，包括横摆角速度（ω）曲线和质心侧偏角（β）；图13为驾驶权动态决策结果（k1，k2）；图14为控制回路输出量，包括驾驶员输出量（δd）和控制器输出量（δc）。

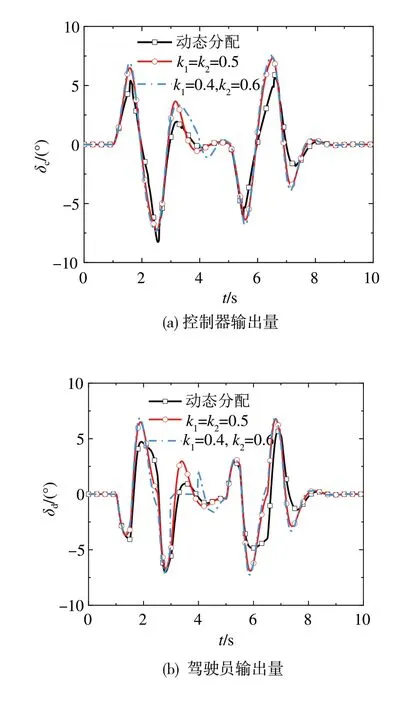
图14 双回路输出量

从图11（a）可以看出，当超车过程中出现突发侧风时，因为最大侧向位移误差eymax为1.06 m，航向角最大误差eφmax为0.12 rad，最大侧向位移误差超过了设定的阈值（1 m）。当超车结束时，驾驶员无法使车辆快速回到直线轨迹。相对于驾驶员，SSC系统可以很好地跟踪超车轨迹。驾驶权分配系数固定为k1=k2=0.5的SSC系统的最大侧向位移误差为0.84 m，最大航向角误差为0.13 rad，轨迹跟踪能力评价指标J1为0.67。相对于驾驶权分配系数固定的方法，本文所提方法的最大侧向位移误差下降了3.57%，最大航向角误差下降了7.69%，J1下降了16.42%。说明所提方法的轨迹跟踪能力得到显著提升。

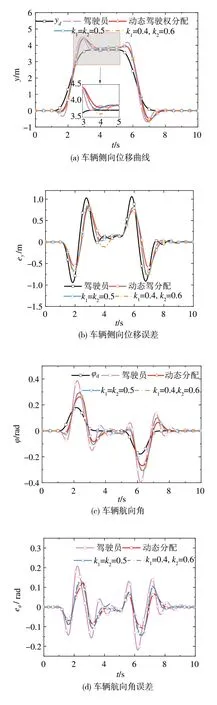
图11 车辆轨迹跟踪状态

从图12可以看出，相对于SSC系统，驾驶员的最大横摆角速度和最大质心侧偏角均增加，超过50%，且超车结束后横摆角速度和质心侧偏角不能收敛到0。但SSC系统的横摆角速度和质心侧偏角可以在超车结束后迅速收敛。这说明SSC系统具备更好的动力学稳定性。

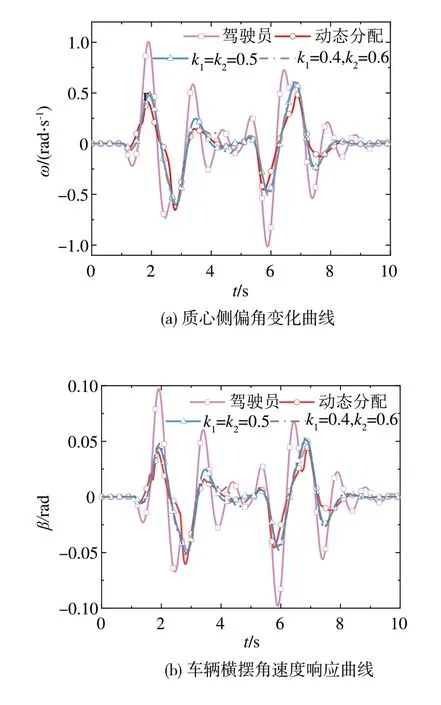
图12 车辆动力学响应

从图13可以看出，在超车过程中，由于车辆轨迹跟踪状态不断发生变化，导致驾驶权动态决策结果也在不断发生变化。特别是在两次换道开始和结束过程中，由于轨迹跟踪误差较大，导致k2也出现阶跃性变化。

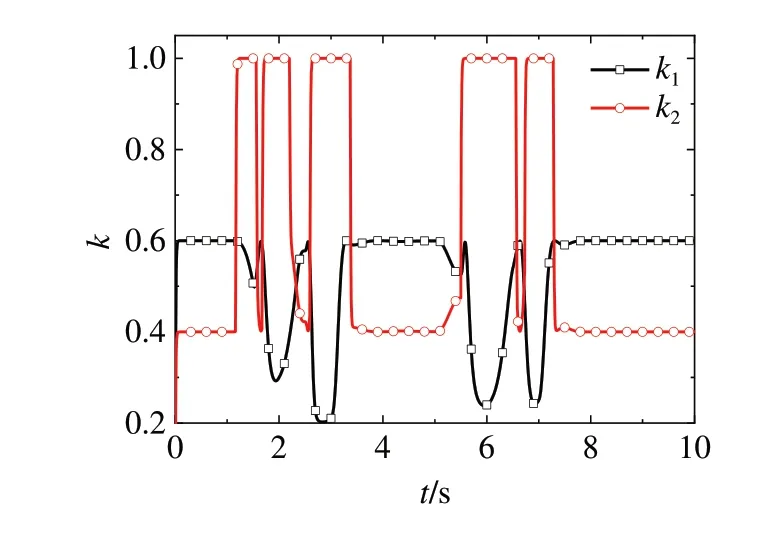
图13 驾驶权动态决策值

图14中，驾驶权分配系数固定方法的δc和δd的波动幅度明显大于本文提出的方法。从统计结果来看，相对于驾驶权分配系数为k1=k2=0.5的SSC系统，本文所提方法的驾驶员操作负荷J2、心理负荷J3以及控制器工作负荷J4分别下降了13.29%、17.01%和6.03%。这表明所提系统不仅可以保证车辆具备很好的轨迹跟踪能力和动力学响应，且可以有效降低驾驶员操作负荷、心理负荷以及控制器工作负荷。

5 结论

为了解决因驾驶员和控制器驾驶权分配系数之和被约束导致的SSC系统控制精度下降问题，以及提高SSC系统的稳定性和可靠性，本文提出了一种驾驶权动态分配方法，所提方法可以根据车辆轨迹跟踪状态和驾驶员状态对驾驶权进行动态分配；同时设计了考虑模型参数不确定性的鲁棒控制器。仿真结果表明：

（1）所提出的方法可以有效提升车辆的抗干扰能力。当驾驶员出现误操作和突发侧风时，相对于驾驶权分配系数固定的方法，所提方法具备更好的车道线保持能力，最大侧向位移误差下降6.67%，轨迹跟踪性能评价指标J1下降6.67%。

（2）所提出的方法不仅具备良好的轨迹跟踪能力和动力学响应，还能有效降低转向操作过程中的驾驶员操作负荷、心理负荷以及控制器工作负荷。SSC系统依然可以在侧风环境下完成超车。相对于驾驶权分配系数为k1=k2=0.5的SSC系统，所提方法超车过程中突发侧风时，最大侧向位移误差下降了3.57%，最大航向角误差下降了7.69%，车辆轨迹跟踪性能评价指标J1下降了16.42%；驾驶员操作负荷J2、心理负荷J3和控制器工作负荷J4分别下降了13.29%、17.01%和6.03%。