流体-流体相互作用模型的无条件稳定格式∗
2022-12-07李伟黄鹏展
李伟,黄鹏展
(新疆大学数学与系统科学学院,新疆乌鲁木齐 830017)
0 引言
在计算流体力学中,两种互不相溶流体的多区域多物理场耦合数值模拟是许多科学和工业应用中的一个重要内容, 例如环境工程中的大气海洋相互作用问题、血流异质性的模拟等等. 这些实际问题可以由两个不可压缩牛顿流体的Navier-Stokes 方程通过摩擦型界面条件耦合来模拟, 这里要求界面满足刚性耦合条件, 即没有流体穿过交界面.
我们考虑Ω ⊂R2是一个有界的区域, 该区域有两个子域Ω1和Ω2且两个区域的界面为I. 设计算时间为t ∈(0,T], 求速度 ui:(0,T]×Ωi→R2和压力 pi:(0,T]×Ωi→R,i=1,2,满足如下方程 (t ∈(0,T])[1]

其中|·|表示欧几里得范数, ui,0∈H1(Ωi)2是初始速度. 这里的νi>0 表示运动粘性, κ>0 是摩擦系数, 外力项fi:[0,T]→ H1(Ωi)2. 向量 ni是 ∂Ωi上的单位法线, τ 是 I 上的任意切向量, 使得 τ ·ni=0. 注意到该流体-流体相互作用模型在I 上采用了非线性界面条件.
由于模型(1)在实际应用中的重要性, 许多研究工作致力于构造高效的解耦方法[2−7]. 最近, 基于解耦时间步长方法, Connors 等[1]提出了两种解耦时间步长方法,第一种是隐式/显式格式,它是最简单和最自然的解耦方法. 随后, Zhang 等[8]证明了该格式是条件稳定的. 另一种是几何平均格式, 该格式是无条件稳定[1]. 但是这些方法都不是以显式格式处理界面项.我们知道显格式虽然计算简便,但是会产生稳定化条件.故构造无条件稳定的显格式就显得尤为重要. 因此, 本文将使用全显式的方法来解耦非线性界面条件.
本文主要构建并研究了一种无条件稳定的有限元方法来求解非线性流体-流体相互作用模型. 新方法具有以下优点: (1) 与隐式/显式格式和几何平均格式不同, 非线性界面条件采用显格式, 计算简便易于实现; (2) 新方法是无条件稳定的. 首先介绍了所研究问题的一些符号、函数空间和一些重要结果. 其次提出了具有显式格式的界面解耦方法, 描述了求解过程, 并推导了算法的无条件稳定性. 最后设计了一些数值实验来验证该方法的稳定性和有效性.
1 预备知识
在本节中, 将给出一些必要的定义和等式. 对于L2(Ωi)空间, 我们分别用‖·‖0和(·,·)来表示其范数及其内积. 接着, 我们用H1(Ωi)表示Sobolev 空间W2,1(Ωi). 对于非线性流体-流体相互作用模型(1), 引入以下压力和速度函数空间: 对于i=1,2, 有

接下来, 我们在 Xi×Xi和 Xi×Mi上定义两个连续的双线性形式 a(·,·)和 d(·,·)如下:

以及在 Xi×Xi×Xi上定义一个非线性项 b(·,·,·)[9]
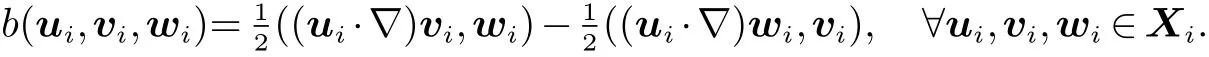
在以上函数空间的定义下, 我们给出问题(1)的变分形式如下, 求ui:(0,T]→Xi和pi:(0,T]→Mi, 使得对于任意的 (vi,qi)∈Xi×Mi,i,j=1,2,i/=j 满足

2 流体-流体相互作用模型的全离散有限元算法
2.1 修正的标量辅助变量技巧
标量辅助变量方法最早基于能量不变二次化方法提出, 应用于梯度流问题[10]. 通过引入标量辅助变量, 可以对原偏微分方程进行修改. 在时间离散系统中, 通过动量方程与辅助变量方程的求和可以消除修改后动量方程中的非线性项. 本文基于标量辅助变量方法思想, 构造一个修正的标量辅助变量. 这时, 非线性界面耦合条件可以在时间离散系统中抵消.

这时, 修正的标量辅助变量Q 对于t 的导数写作

注意到, 对(4)中界面项求和等于零,
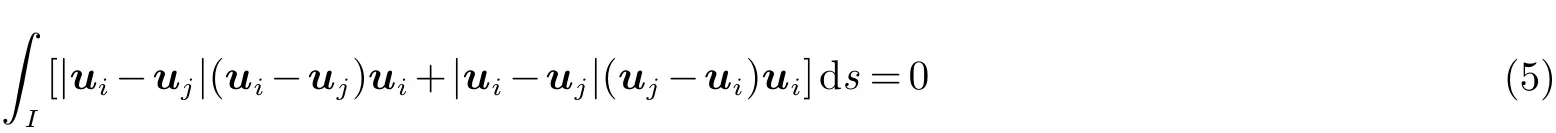
在连续情形下(1+t)Q=1, 故(1)式结合修改的界面条件(3)的解与原问题(1)的解相同.
对应的(1)与(3)组成系统的变分形式如下, 求ui:(0,T]→Xi和pi:(0,T]→Mi, 对于∀(vi,qi)∈Xi×Mi,i,j=1,2, i/=j 满足

2.2 基于修正标量辅助变量的全离散有限元方法
首先, 对于N>0, 令{tn}Nn=0是对[0,T]均匀划分得到的时间剖分, 其中时间步长∆t= NT并有 tn=n∆t. 对于 i=1, 2, 令 πih是子区域Ωi上的三角形剖分并定义为πh=π1h∪π2h, 其h 是πh上三角形单元的最大外接圆直径. 此外, 在 πih上速度和压力的离散空间分别记为Xih⊂Xi和Mih⊂Mi. 其有限元离散子空间定义如下:

其中: 对于∀Ki∈πih,P1(Ki)表示定义在Ki上的最高次数为1 次的多项式,ˆb ∈H01(Ki)为在单元Ki上重心取值为1 的函数,并满足0 ≤ˆb ≤1.众所周知,该有限元空间配对Mih和 Xih满足离散的 Ladyzenskaja-Babu˘ska-Brezzi条件

其中: βi>0 为只依赖于区域Ωi的正常数. 更进一步, 记(uni,h,pni,h)为模型(1)在t=tn的有限元近似解. 最后,记fin=fi(tn).
基于修正标量辅助变量Q, 时间离散采用向后Euler 方法, 得到全离散的有限元方法:
给定(uni,h,pni,h)∈ Xih×Mih和 Qn∈ R, 对于 1 ≤ n ≤ N −1, 求 (uni,+h1,pni,+h1)∈ Xih×Mih和 Qn+1∈ R 使得对于∀(vi,h,qi,h)∈Xih×Mih, i,j=1,2, i/=j,满足

注意到,在算法(7)∼(8)中,(un+1i,h, pn+1i,h)和(un+1j,h, pn+1j,h)是解耦计算的. 但它们仍与Qn+1耦合在一起,因此构建的离散系统需要解耦才能达到较高的计算效率.
现在, 开始描述如何有效地应用全离散方法(7)求解模型(1). 记Sn+1=(1+tn+1)Qn+1. 令

将式(9)代入式(7), 并整理得:

基于(10)∼(11)得到的˜un+1i,h和¯un+1i,h, i=1,2, Sn+1可以从标量方程(8)计算得出, 其计算方程如下:
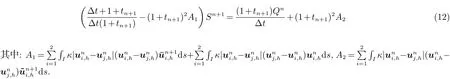
最后, un+1i,h和pn+1i,h(i=1,2)可以由式(9)得出.
2.3 稳定性分析
在本节中, 研究所提出的全离散有限元算法(7)∼(8)的稳定性.

则有如下不等式成立
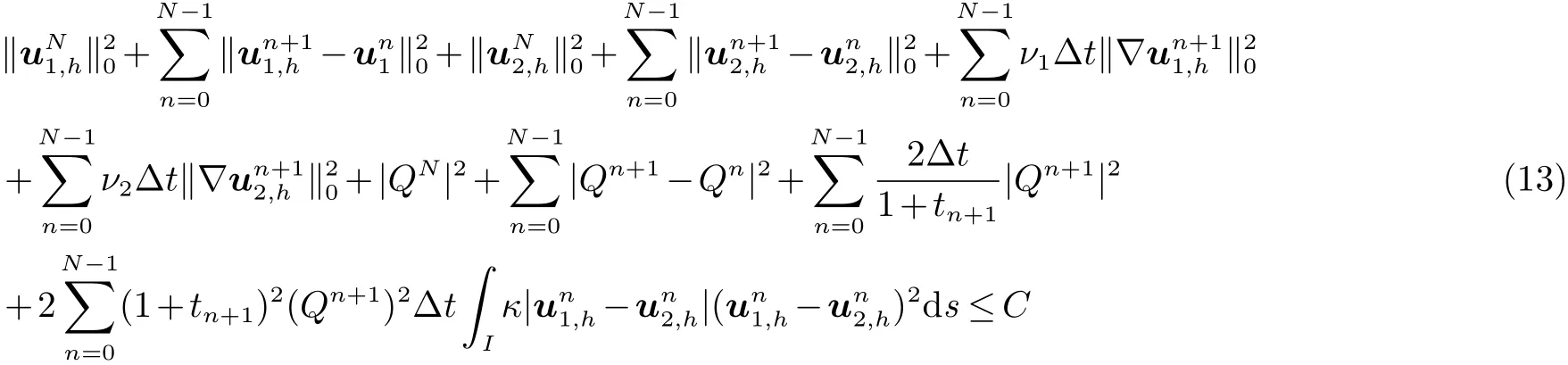
证明 令(7)式中(vn+1i,h,qn+1i,h)=2∆t(un+1i,h,pn+1i,h)得

这里我们使用了等式2(a−b,a)=|a|2−|b|2+|a−b|2, ∀a, b ∈Rd和非线性项的反对称形式性质.
标量方程(8)乘2∆tQn+1可得

将(14)式和(15)式结合得

此外, 对于(16)的右端项, 有
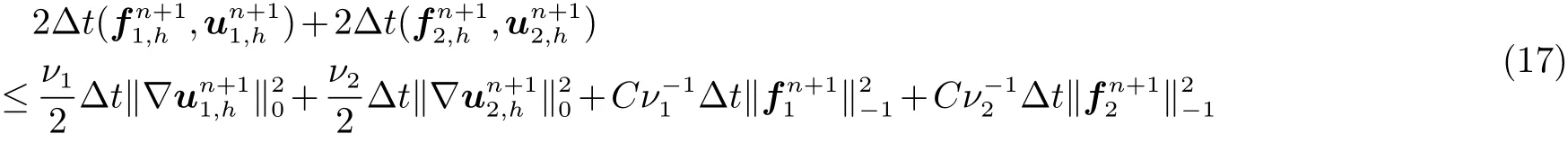
结合(16)式和(17)式得
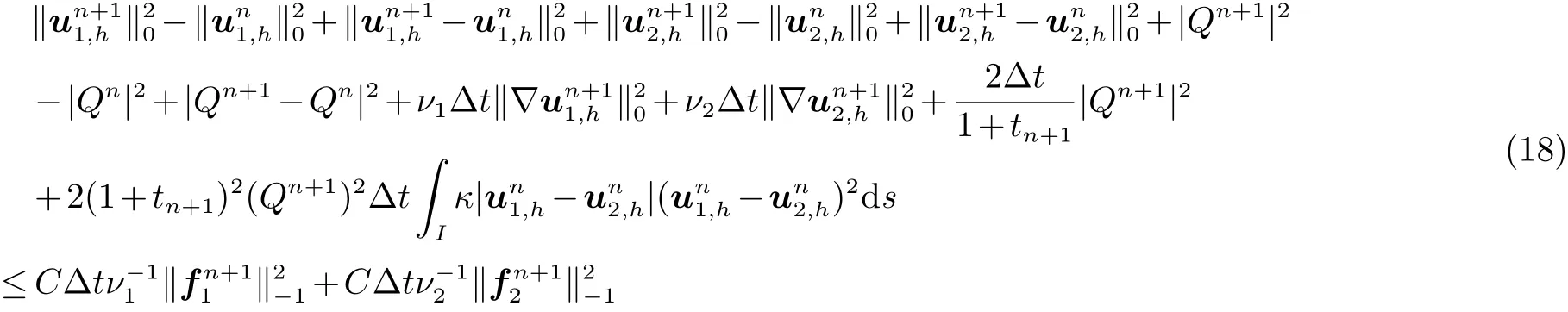
最后, 对 (18)式从 n=0, 1, 2,···N −1 求和, 即完成了证明.
3 数值模拟
在这一节中, 通过一些精确解数值实验来测试式(7)∼(8)的稳定性和收敛性. 除此之外, 通过Aggul 等[11]提出的一个实际问题(海岸山或悬崖问题)来测试算法长时间计算的有效性.
3.1 无条件稳定性验证
在本节中, 通过一个初值问题测试当前算法(7)∼(8) 的稳定性. 假设Ω = Ω1∪Ω2且 Ω1= [0,1]×[0,1],Ω2=[0,1]×[−1,0]. 显而易见, I=(0,1)×{0}. 在 I 上, n1=[0,−1]T, n2=[0,1]T. 在本算例中除界面外,其余边界选择为齐次的Dirichlet 边界条件, 并且设置其外力项fi=0, i=1,2. 选取初始值如下以满足无散度条件,

固定空间步长 h=1/32,参数选取为 ν1=2.0e−2, ν2=5.0e−2, κ=1.0. 记 E(ui)=Ωi(u2i,1+u2i,2)dx. 选择最终时间为T =5. 图1 展示了当前算法在不同时间步长∆t=0.1, 0.05, 0.01 时能量衰减结果.由图1 可知,所有的能量曲线都呈现单调的衰减. 此外, 我们发现该算法的数值结果并不会随着时间步长变长而发散, 从而在数值上证实了当前方法的无条件稳定性.
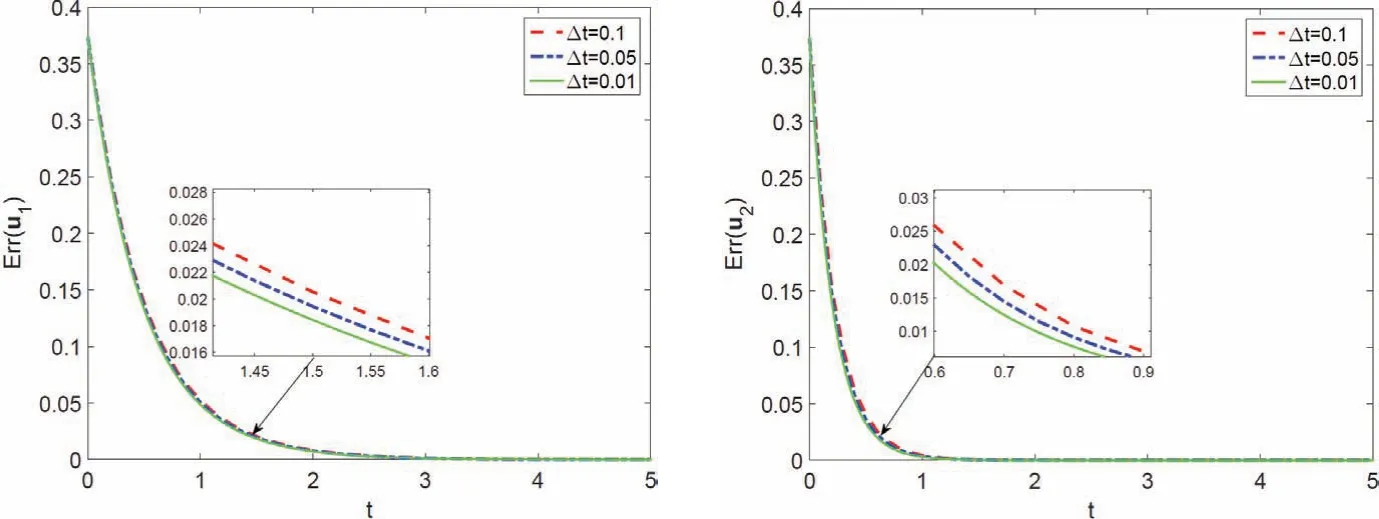
图 1 能量耗散图:Ω1 (左)和Ω2 (右)
3.2 收敛率验证
本节考虑一个解析解问题来验证算法的收敛率. 令Ω1=[0,1]×[0,1],Ω2=[0,1]×[−1,0]且I=(0,1)×{0}. 模型(1)的解析解如下所示:

右端项f1=(f1,1(t,x,y),f1,2(t,x,y))和f2=(f2,1(t,x,y),f2,2(t,x,y))的选择必须满足(u1,p1)和(u2,p2)是式(1)的解. 为了简便起见,误差简记为:

固定参数ν1=0.05, ν2=0.5,κ=100, 选取5 个不同的空间步长h=1/4, 1/8, 1/16, 1/32 和1/64 验证空间收敛率. 此外, 固定时间步长∆t=h 验证时间收敛率.
图2 和图3 分别展示了当前算法在Ω1和Ω2子域上所得的误差及收敛率. 由图2 和图3 可以看到当前的算法表现良好, 并保持了速度、压力的最优收敛速度. 一阶时间精度也得到了验证.
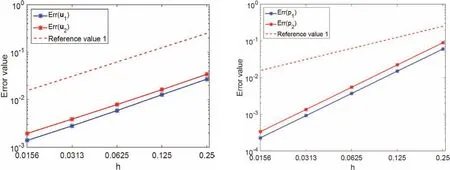
图 2 空间收敛率: 速度场(左)和压力场(右)

图 3 时间收敛率: 速度场(左)和压力场(右)
3.3 海岸山或悬崖问题
考虑一个海岸山或悬崖实际问题用于验证当前算法的长时间稳定性. 该问题描述大气层中以抛物线流入海岸山或悬崖上空的气流与海水相遇时的现象. 计算区域与文献[11]一致. 在此区域中, 在海岸山或悬崖边界, 以及海洋底部施加了齐次的Dirichlet 边界条件. 同时, 大气中的流体流动是以抛物线入口流入, 对其它边界不设置边界条件.
固定ν1=0.005,ν2=0.05,κ=0.001,h=1/10 和τ =1/5,取不同的最终时间所得到的速度矢量图和压力轮廓图如图4∼图7 所示. 从图中可以看出, 当前算法是稳定的且并未出现不符合物理的振荡. 此外,使用该方法所得出的模拟结果与Aggul 等在文献[11]中所得到的结果保持一致.

图 4 速度矢量图: T =5(左)和T =10(右)
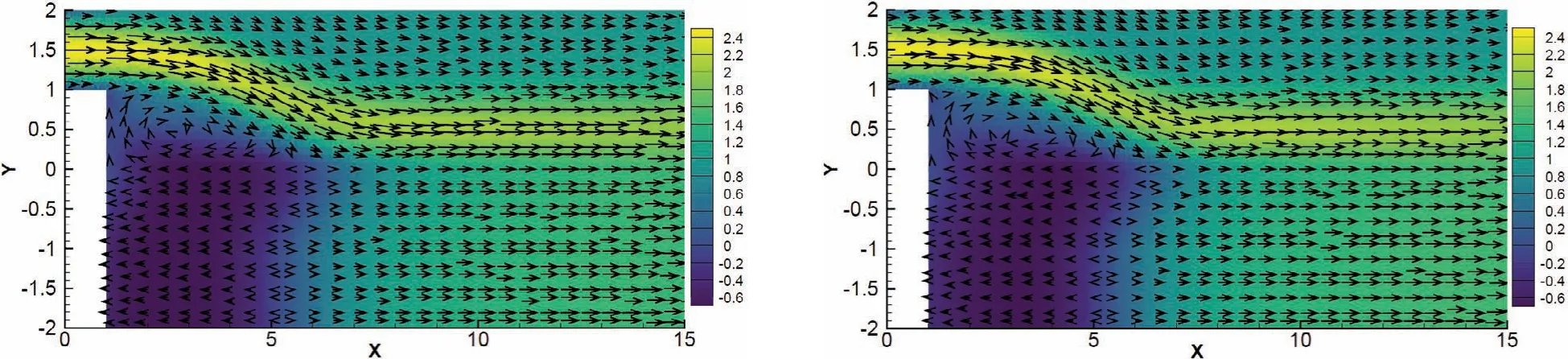
图 5 速度矢量图: T =20(左)和T =40(右)

图 6 压力轮廓图: T =5(左)和T =10(右)

图 7 压力轮廓图: T =20(左)和T =40(右)
