混合拉伸模式下介电弹性体发电性能研究∗

余国晖，陈洁，李宝权，李玉麒

(新疆大学电气工程学院，新疆乌鲁木齐 830017)

0 引言

介电弹性体材料作为一种变形可控的电活性聚合物，可以在外加电压的作用下表现出快速的驱动响应和良好的发电响应[1−3]. 介电弹性体具有能量密度高、重量轻、变形大、响应快等优点，可以制造出多种形状以及成本低的材料. 这些特点使它们比其它电活性聚合物更具有竞争优势. 在过去的十几年里，研究人员已经提出了许多基于介电弹性体材料的执行器[4]和发电机[5−8]的案例.

近年，人们通过优化介电弹性体膜的材料性质、拉伸方式和电路设计来提高介电弹性体发电机的发电性能[9−10]. 最常见的拉伸模式包括单轴拉伸、等轴拉伸、锥形拉伸和充气圆形隔膜模式[11−12]. 与其它拉伸方式相比，虽然等轴拉伸模式能够获得最高的能量收集性能，但由于其拉伸结构复杂和材料的高延展率，导致其缺乏实用性. 而锥形拉伸模式的结构非常简单，它仅要求直线运动，这是一种非常常见的运动模式，可以直接应用于电机或者活塞运动，因此它可能是目前最有前途的介电弹性体发电机的应用模式[13]. 所以本文采用等双轴预拉伸和锥形拉伸相结合的方法，系统地研究了介电弹性体发电机在Neo-Hookean本构模型下的机电不稳定模型和能量收集性能.

1 介电弹性体发电理论

介电弹性体作为一种超弹性绝缘材料，在其上下表面涂覆上柔性电极即可作为可变电容器使用，通过拉伸收缩改变施加偏置电压前后的电容来进行发电. 其可变电容表达式为：

其中：ε0是真空中的介电常数（约为8.85×10−12F/m）；εr是材料的相对介电常数；S是柔性电极的涂覆面积；d是薄膜的厚度.

在释放机械变形的同时保持电容器上的电荷恒定，其电荷与电压之间的关系为：

其中：C1是拉伸前的电容值；V1是一个循环后的输出电压；C2是拉伸到最大处的电容值；V2是施加的偏置电压.

因此，介电弹性体发电机在一个循环内从拉伸再到收缩后产生的电能为：

其中电能产生的多少由偏置电压和变形前后电容比共同作用. 因此介电弹性体发电机的最大能量输出取决于其拉伸极限和电击穿强度，这通常被称为边界条件.有研究通过模拟计算优化了基于边界条件下的能量输出[14]，但很少有关于边界条件下的机电耦合模型[15]，故本文采用等双轴预拉伸和锥形拉伸结构相结合的方法，建立了基于Neo-Hookean模型的介电弹性体的机电不稳定模型和机电耦合模型. 然后分析了在不同预拉伸条件下介电弹性体发电机的能量收集性能. 介电弹性体发电机制作流程如图1所示.

图 1 介电弹性体发电机制作流程

2 介电弹性体的机电不稳定性模型

在未变形的初始状态（X, Y, Z）采用等双轴预拉伸，如图1所示，预拉伸后的材料尺寸为（x′, y′, z′），即预拉伸比为：

将介电弹性体膜制成锥形介电弹性体发电机后，考虑到施加电压后介电弹性体膜会沿内框和外框的同轴方向延伸，但由于其固定在刚性圆盘上，所以在y轴方向上保持不变，其变形模式类似于纯剪切拉伸，即有：

根据其热力学系统的自由能和体积计算出单位体积的自由能密度函数为：

由公式（6）和（7）得出广义机电不稳定模型的一般表达式为：

该模型可直接应用于Neo-Hookean模型：

其中：µ是材料参数，λ1、λ2、λ3是各方向上的拉伸率.

所以Neo-Hookean的机电不稳定模型为：

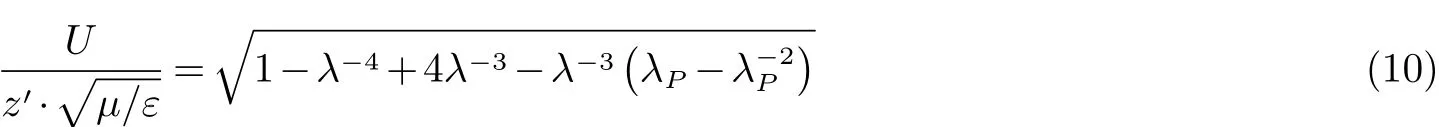
3 机电耦合建模与仿真

进行实验之前，利用Matlab/Simulink软件建立了介电弹性体发电机系统的模型，并利用仿真模型解释了该系统的能量转换规律.

3.1 介电弹性体的力学模型

连续介质力学中，介电弹性体被认为是一种具有大变形的超弹性材料，即需要本构模型来描述其应力应变关系. 本文选用Neo-Hookean本构模型来描述其应力应变关系，并结合电气模型建立了介电弹性体发电机的机电耦合模型. 由于介电弹性体膜用亚克力板固定，所以其变形模式类似于纯剪切拉伸模式，初始尺寸为：

介电弹性体材料在各个方向上的柯西应力表示为：

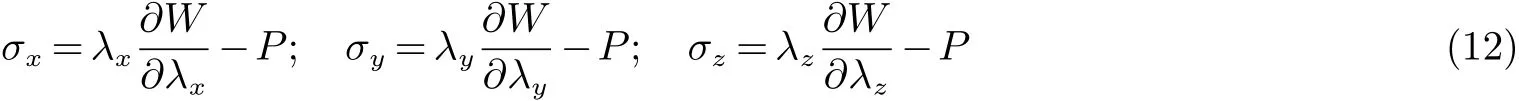
其中：P为动力学的边界条件静水压力. 由于在y方向上没有变化，所以λy=1、σy=0.

在介电弹性体换能器两端施加了偏置电压U，所以z方向上存在麦克斯韦静电力表示为：

其中：Q是介电弹性体发电机两端的电荷.

联立公式（9）、（12）和（13）可以求出σx为：

由于类似纯剪切拉伸模式，所以：

把公式（15）代入（14）中可得：

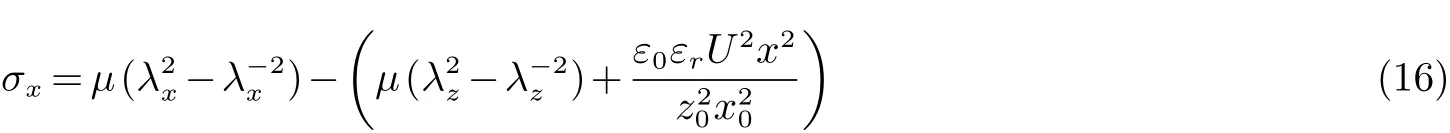
根据牛顿第二定律，对介电弹性体发电机沿x轴进行受力分析可得：

将公式（16）代入（17）中可得：

其中：dv是阻尼系数，设置值为1.

3.2 介电弹性体的电学模型

介电弹性体发电机的本质是通过可变电容结构将机械能转化为电能，其电容可表示为：

上、下表面的电势差为：

对时间进行求导可得：

根据图2建立的介电弹性体电气模型可得：

其中：U0是介电弹性体发电机的初始电压；i为回路电流；R1是等效电阻.

式（23）即为介电弹性体发电机在混合拉伸下的电学模型：

图 2 介电弹性体电气模型

3.3 仿真分析

式（18）和（23）构成了介电弹性体发电机的机电耦合模型. 本文使用Matlab/Simulink建立其仿真模型，为了简化运算过程，代入已知条件合并同类项，该模型被化简为：

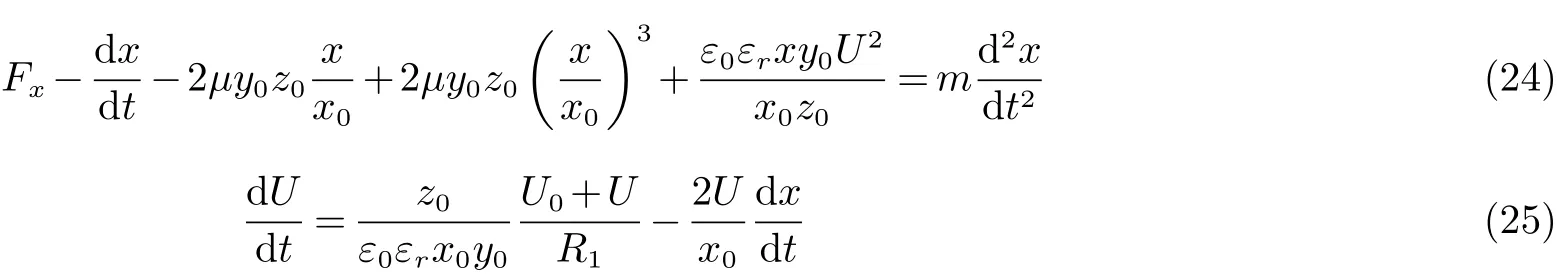
根据上述等式，在Matlab/Simulink中介电弹性体发电机的仿真模型如图3所示.

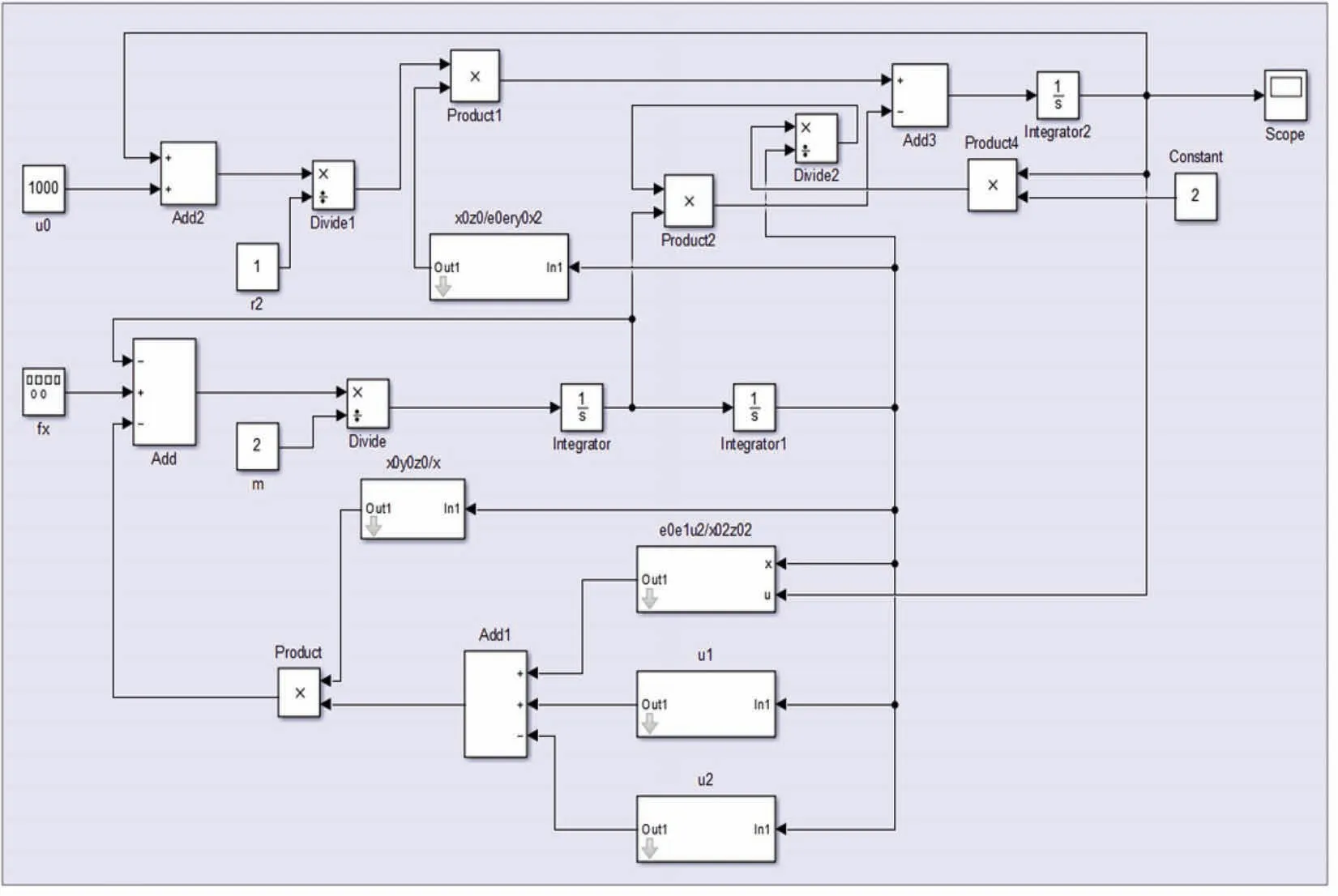
图 3 Matlab/Simulink仿真模型图

仿真曲线如图4所示，在介电弹性体发电机的发电循环中，介电弹性体膜将重复拉伸然后收缩，在收缩过程中，介电弹性体发电机克服电场力将机械能转换为电能，因此电压升高. 能量被收集后，又开始下一次新的拉伸收缩循环.

图 4 仿真模拟图

3.4 实验平台

通过数字万用表直接测量了不同拉伸位移下的锥形介电弹性体的电容值，并按电路图连接在如图5所示的实验台上. 介电弹性体材料选用3M公司的VHB4910型聚丙烯酸橡胶、柔性电极材料选用型号为DDG-A型的导电膏，选用示波器（TBS 1052B-EDU）、万用表（VICTOR VC890D）、高压发生器以及模拟电路实验箱（THM-1型）.

图 5 实验平台

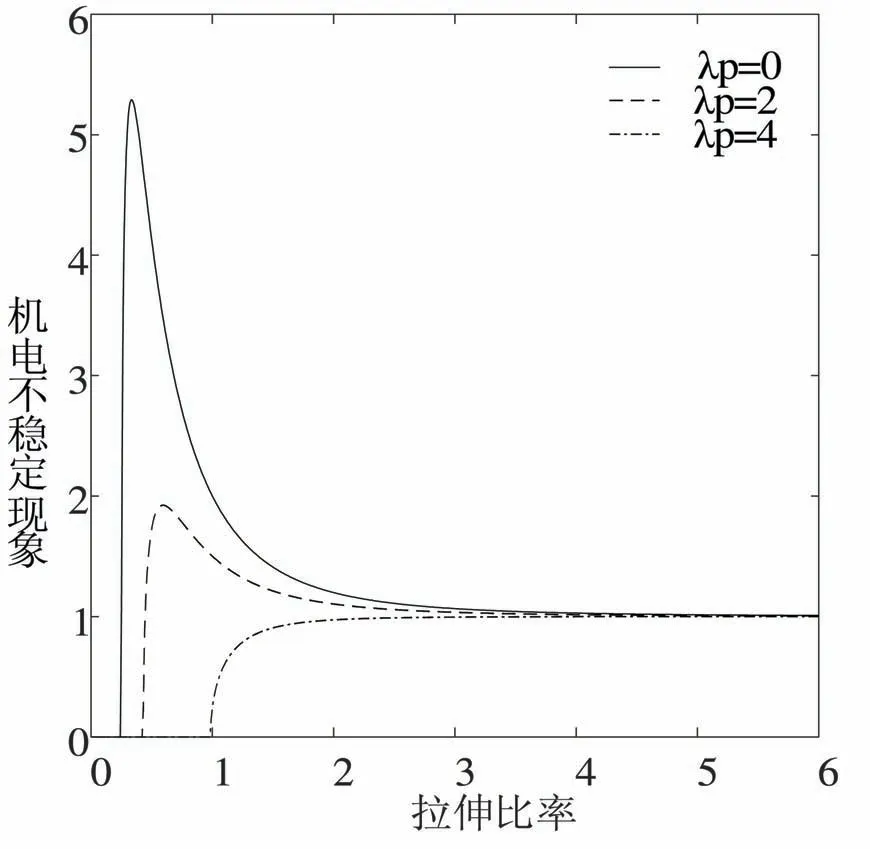
图 6 机电不稳定性比较图

基于前一节描述的能量产生原理，介电弹性体发电机可以通过拉伸收缩循环来收集能量. 其中两种类型的能量涉及电能的增加和机械能的损耗. 对介电弹性体发电机的能量收集实验步骤如下：（1）将介电弹性体发电机接入测量电路；（2）将锥形介电弹性体发电机拉伸到指定位移处，即输入机械能；（3）施加偏置电压给介电弹性体发电机充电；（4）释放机械能让薄膜收缩，将机械能转换为电能；使用万用表测量出其输出电压，即可以通过公式来计算产生的电能.

在该机械卸载期间，弹性体的厚度增加，并且通过增加介电弹性体膜的电位将机械能转换为电能. 但在实际实验中，少量的电荷泄露是不可避免的. 因此，选择合适的电容和输入偏置电压可以控制系统的电压大小，使得介电弹性体换能器仍然能在电击穿电压以下，同时还可以优化产生的能量.

4 结果与讨论

研究了介电弹性体发电机的电容、输出电压、产生的能量和能量密度. 此外还研究了预拉伸对模型机电不稳定性的影响.由图6可知，机电不稳定现象出现在没有预拉伸和预拉伸较小的情况下，也就是说预拉伸可以减小机电不稳定现象对系统的影响.

4.1 电容与拉伸位移的关系

根据公式（3），电容的变化可以反映介电弹性体发电机的能量产生性能，在相同的输入偏置电压下，预拉伸可以在很大程度上提升介电弹性体发电机的能量产生性能，而且拉伸程度越大的介电弹性体发电机具有越高的电能和能量密度. 图7给出了不同拉伸程度在不同预拉伸下的电容之间的增长趋势.

图 7 不同预拉伸下电容与拉伸位移关系

图 8 不同施加偏置电压下拉伸位移与输出电压关系

4.2 输出电压与拉伸位移的关系

4.3 优化能量和能量密度

为了优化能量的产生，将拉伸位移最大值设置为略小于介电弹性体薄膜的破裂位移. 图9显示了λP=2（图9(a)）和λP=4（图9(b)）在各种偏置电压下一个工作循环中不同拉伸位移下的介电弹性体发电机产生的能量. 由于拉伸位移的增加，所产生的能量急剧增加. 例如：在λP=2、施加电压为2 500 V、拉伸位移为70 mm的情况下，一个工作循环所产生的能量为44.45 mJ，大约是相同的电压下，拉伸位移为20 mm所产生能量的21倍. 在λP=4、拉伸位移仅为60 mm时，一个工作循环所产生的能量为114.49 mJ.所以预拉伸有助于提高系统的能量收集性能.尽管拉伸位移和预拉伸的增加降低了系统的临界电压，但在最大电压下产生的能量仍然急剧增加.

能量密度也是一个非常重要的能量采集性能指标，它可以通过将产生的能量除以介电弹性体膜的质量来计算. 因此，除了纵坐标的比例不同之外，其它图表的趋势与产生的能量趋势非常相似. 由图10可知，随着偏置电压的增加或者锥体拉伸位移的增加，能量密度显著提高.

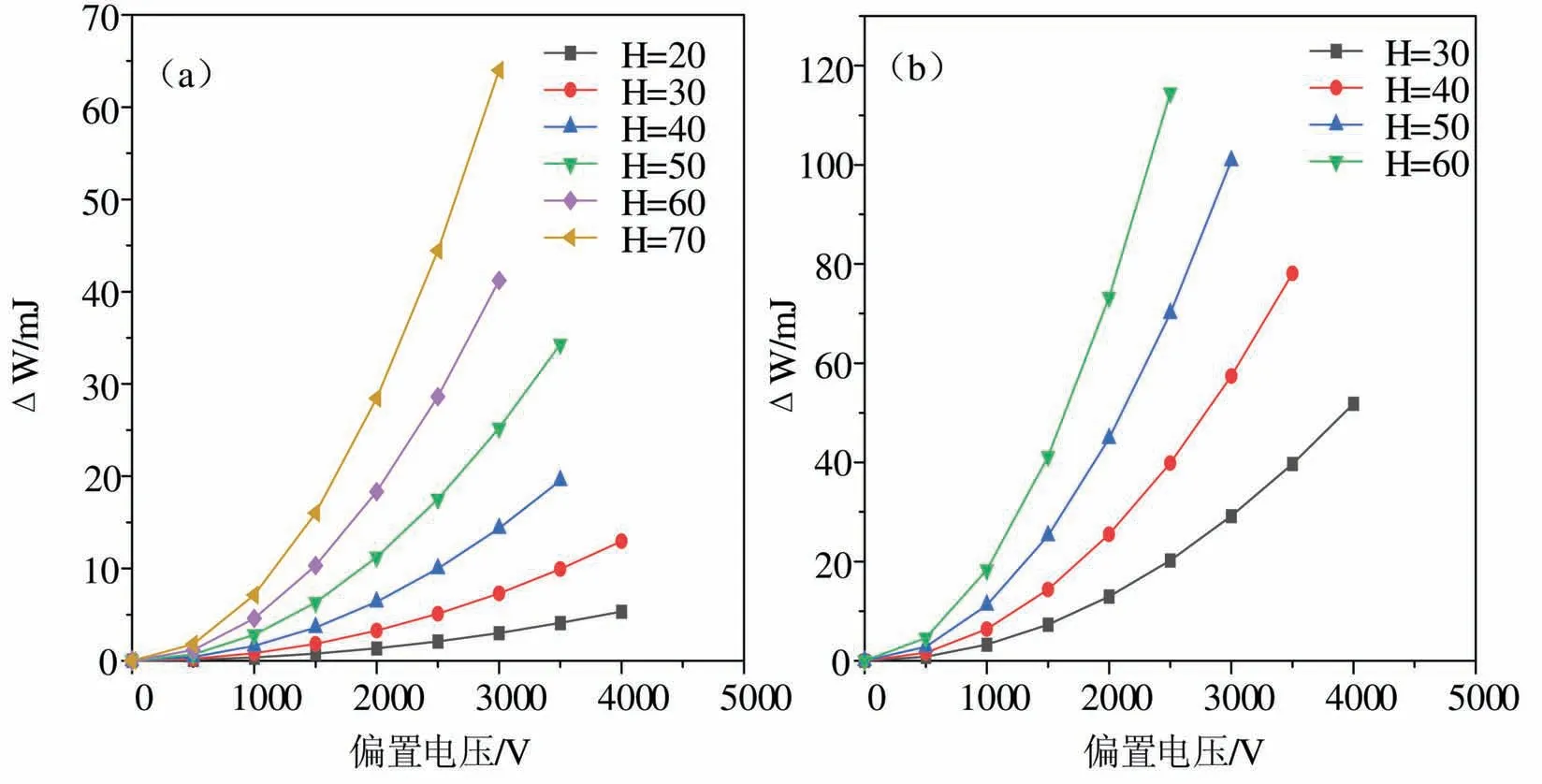
图 9 不同预拉伸下不同偏置电压和拉伸位移产生的能量

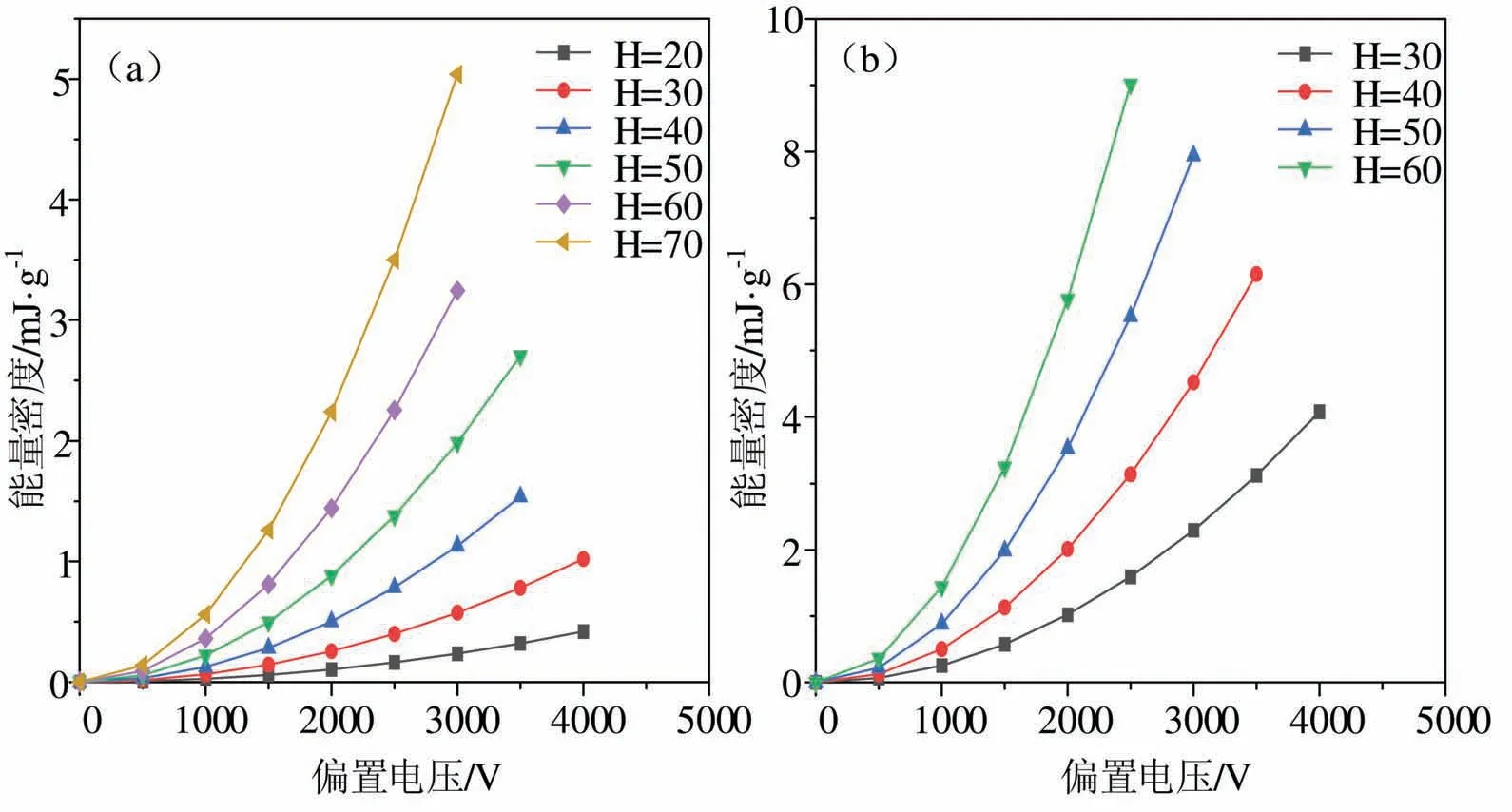
图 10 不同预拉伸下不同偏置电压和拉伸位移的能量密度

值得注意的是，预拉伸有助于在较短的拉伸位移和较低的偏置电压下实现目标能量收集性能，这表明可以在较小的器件结构和较低输入偏置电压下实现高性能，使得整个器件更轻便、具有较高的应用价值.

5 结论

在物理基本定律和热力学理论的框架内，推导了介电弹性体材料在等双轴预拉伸和锥形拉伸相结合的情况下，将所建立的材料变形定律应用于Neo-Hookean模型的介电弹性体材料的机电不稳定模型. 结果表明：在使用前对介电弹性体材料进行预拉伸可以有效改善其机电不稳定的影响，即预拉伸比越大，机电不稳定性对模型的影响越小. 在本文所建立的机电耦合模型中，介电弹性体换能器能克服电场力将机械能转换为电能，所产生的能量最高达到114.494 mJ，能量密度最高达到9.015 mJ/g，是预拉伸比为2时的4倍. 总而言之，混合拉伸模式下的介电弹性体发电性能得到了巨大的提升. 在较短的拉伸位移和较低的偏置电压下，预拉伸对实现目标能量收集性能起着至关重要的作用. 而且采用等双轴预拉伸和锥形拉伸相结合的方式不仅有效地提高了介电弹性体换能器的能量收集性能，还具有较高的实用性.