基于DGRU网络的烘丝机筒壁温度动态预测
2022-12-07张雷李金学堵劲松李龙飞邹严颉张二强李善莲
张雷,李金学,堵劲松,李龙飞,邹严颉,张二强,李善莲
1.郑州轻工业大学 电气信息工程学院,河南 郑州 450001;2.中国烟草总公司郑州烟草研究院,河南 郑州 450001;3.河南中烟工业有限责任公司 技术中心,河南 郑州 450000;4.陕西中烟工业有限责任公司 技术中心,陕西 西安 710065
0 引言
叶丝干燥是卷烟制丝生产的核心工序,卷烟成品的品质控制十分重要,其任务是改善烟丝物理特性、提高感官品质。滚筒烘丝机是叶丝干燥的关键加工设备,烟丝经入料口定量进入烘丝筒内,滚筒转动向前传送物料,在加热筒壁和热风的共同作用下,经一系列复杂的物理化学变化,将烟丝干燥至含水率符合规范要求。筒壁温度是过程控制的重要参数,由于滚筒式烘丝机特殊的设备结构和密闭生产空间,实际筒壁温度难以直接在线检测和控制,造成叶丝含水率的波动,进而影响卷烟品质。
目前,常见的烘丝干燥过程建模研究方法是机理模型[1],该方法从化学、热工等角度构建物质反应场,对滚筒内部的物料运动和温度场分布进行仿真,但机理模型大多建立在理想条件下,且需要专家经验积累,难以适应复杂多变的工况。数据驱动建模方法无需任何专家经验,仅依赖工业过程数据质量,借助人工智能技术飞速发展,该方法引起了国内外学者高度关注[2]。数据驱动建模方法主要有神经网络(Artificial Neutral Network,ANN)、支持向量机(Support Vector Machine,SVM)、极限学习机(Extreme Learning Machine,ELM)等[3-4]。神经网络具备强大的泛化能力,能够以任意精度逼近复杂连续函数,特别适用于解决复杂工业过程的非线性建模问题,在钢铁、冶金、建材等流程工业应用广泛。一般神经网络建模多基于稳态工况假设,然而烘丝干燥过程是一类稳态、非稳态交替出现的动态工况,传统方法缺乏对工业数据动态特征处理能力,建立的软测量模型存在一定局限性。
循环神经网络(Recurrent Neural Network,RNN)[5-6]是具备内部反馈结构的动态神经网络算法,在处理时序信号上具有显著优势,广泛应用于语音识别、动态建模、故障诊断中。经典RNN一般采用跨时间梯度反向传播算法(Back Propagation Through Time,BPTT) 优化模型参数,然而很容易产生梯度消失或爆炸及长期依赖问题。为解决上述难题,国外学者提出了长短期记忆单元(Long Short Time Memory,LSTM)[7-9]和门控循环单元(Gated Recurrent Unit,GRU)[10-13],通过设计门函数调节内部神经元的信息交流,从而更易捕捉时序数据中的长期依赖关系。
基于此,本文拟提出一种基于深度门控循环单元(Deep Gated Recurrent Unit,DGRU)网络的烘丝机建模新方法。该方法在数据预处理和特征选择基础上,通过堆叠门控循环单元网络提取制丝数据中深层非线性动态特征,以端对端方式实现筒壁温度动态预测,以期解决烘丝干燥过程中筒壁温度难以准确进行在线测量的问题。
1 数据预处理及特征选择
1.1 数据预处理
在烘丝机生产过程中,采集了物料流量(X1)、入口物料含水率(X2)、HT蒸汽压力(X3)、蒸汽流量(X4)、烘丝累积量(X5)、入口实际水分(X6)、工作蒸汽压力(X7)、区域1冷凝水温度(X8)、区域2冷凝水温度(X9)、热风温度(X10)、热风速度(X11)、罩压力(X12)、烘丝出口温度(X13)这13个过程变量。由于筒体倾斜且不断旋转,现场仪表和传感器采集数据不可避免地含有一定量的随机噪声和离群点,工业原始数据品质通常较差,影响模型预测精度。为了保证软测量模型的可靠性,有必要对采集的数据作预处理,主要包括离群点剔除、小波去噪及归一化处理。
制丝生产现场采集的叶丝干燥数据容易受到各种形式干扰(如传感器故障、过程扰动、状态漂移等),故采用基于小波变换的去噪方法消除数据随机噪声,如下式所示:
f(t)=s(t)+σ·e(t)
其中s(t)为原始信号,f(t)为含噪声信号,e(t)为噪声,σ为噪声标准差。小波变换去噪的主要目的是抑制信号中的高频噪声,从而在f(t)中恢复真实信号s(t),包括小波分解、高频系数的阈值量化处理、信号重构3个步骤,其中小波变换参数选择“Sqtwolog”基函数。
以入口物料含水率为例,预处理对比效果如图1所示。由图1可知,采用小波去噪后,在保持数据主趋势同时,能够减少曲线毛刺,提高建模样本质量。

图1 物料含水率预处理效果Fig.1 Preprocess result of material moisture content
1.2 互信息特征选择
烘丝机干燥过程变量(控制参数和状态变量)存在一定相关性和冗余性,如果建模中直接采用全部变量,容易增加模型复杂度,导致预测准确率下降和收敛速度缓慢。因此,本文采用最大相关最小冗余算法(Maximum Relevance and Minimum Redundancy,mRMR)[14],选择与筒壁温度相关性最强的特征作为模型初始输入变量。集合S中变量X和输出Y的最大相关性定义为:
其中,S为集合中变量个数,原始变量间可能存在一定冗余性,因此,最小冗余定义为:
则最终目标函数为:
maxφ(D,R)=D-R
式中φ代表变量相关性较大同时与其他特征相似性较小的特征。实践中常采用增量式策略搜索最优特征集合。
2 基于DGRU网络的筒壁温度动态建模
2.1 门控循环单元
烘丝干燥过程运行工况复杂多变,传统浅层GRU网络特征提取能力有限,难以准确反映实际工况动态变化。本文通过堆叠GRU提取工业数据中深层非线性动态特征,将其输入全连接层用于估计筒壁温度。GRU 是一种特殊的RNN单元,在RNN基础上添加更新门zt和重置门rt,通过门控单元控制内部神经元信息传输。相对于LSTM算法,GRU网络参数更少,在保证预测精度前提下,提高收敛速度。GRU网络基本结构如图2所示。

图2 GRU网络基本结构Fig.2 The structure of GRU network
在GRU中,对应t时刻隐层的输入xt,更新门zt,重置门rt,隐层输出ht,上一时刻隐层输出的计算方式如下所示:


2.2 全连接层网络
堆叠GRU网络提取烘丝机运行数据中隐含的动态信息后,将其作为输入变量送入全连接层网络,用于建立辅助变量与筒壁温度之间的预测模型,以端对端方式实现筒壁温度在线预测。全连接层网络定义如下:
oi=g(Wihi+bi)
其中,oi和hi分别代表第i个全连接层的输出和输入,Wi和bi代表第i个全连接层的权值和偏置。
2.3 DGRU算法流程
基于DGRU的筒壁温度动态预测算法流程如图3所示,离线训练和在线预测步骤如下。

图3 基于DGRU的筒壁温度动态预测算法流程Fig.3 Flow chart of cylinder wall temperature prediction by DGRU Algorithm
离线训练:
1)采集现场工业数据,进行预处理;
2)采用mRMR方法进行特征选择,确定最佳输入变量;
3)确定合适的延迟时间,进行输入变量时序重构;
4)确定模型结构和参数,将时序数据按一定比例划分为训练集和测试集;
5)DGRU算法中采用双层网络结构,其中激活函数为tanh,并采用BTTP算法对DGRU模型进行训练;
6)确定全连接层网络参数,采用梯度下降法训练,若精度满足要求则训练结束,否则重复步骤5)。
在线预测:
7)对任意测试数据进行预处理、特征选择、时序重构操作;
8)基于已训练的DGRU模型,计算模型输出;
9)反归一化目标输出值,获取最终预测值。
3 工业实验验证及结果分析
3.1 建立DGRU模型
以河南中烟工业有限责任公司的两段式滚筒烘丝机(简称烘丝机) 为实验对象,烘丝机以一定倾斜角(1.5°~5°)转动运行,烟丝在滚筒前滚动前进,直到出料口落下。物料向前传送,蒸汽在压力输送下,从主管路由旋转接头进入烘丝机,一路进入烘筒内热交换装置,另一路进入热风系统的空气加热器,热风由管道输送到前室进入烘筒,与烟丝充分接触。烟丝在蒸汽加热的筒壁和热风的共同作用下,完成叶丝干燥。
从现场DCS数据库中采集2020年1月2日至2020年2月28日生产数据进行仿真实验,在实际干燥工艺中,一般更注重烘丝机区域1的温度控制,因此本文以区域1温度作为模型输出。此外,原始叶丝干燥数据包括料头、料尾段,这些数据不利于建模,因此选取稳定生产阶段数据。采样间隔10 s,实验数据如表1所示。
实验测试环境如下:OS为 Windows 10教育版 (64 bit);CPU为Intel(R) Core(TM ) i7-11700 2.50 GHz;RAM为16.0 GB;Python版本为3.6.0;TensorFlow-GPU 版本为1.12.0。为了验证本文方法的有效性,将DGRU算法与经典ELM、RNN和GRU算法对比,ELM采用Matlab2018版本,激活函数为Sigmoid,采用单隐含层结构,节点数为40。RNN、GRU分别采用单隐含层网络架构,隐含层单元个数设置为140,最大迭代次数为 100,时间步长为1,初始学习率为 0.000 1。同时采用Dropout技术,以避免训练过程中的过拟合问题。DGRU算法模型参数见表2。
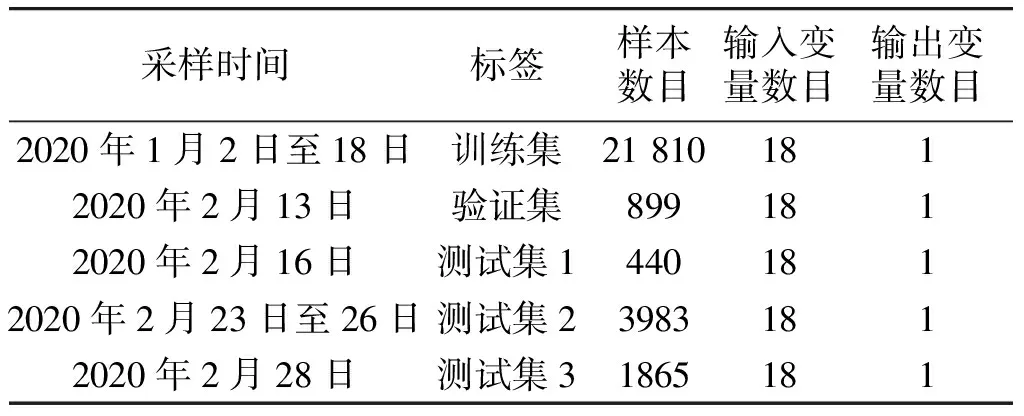
表1 实验数据信息Table 1 Information of experimental data
此外,滚筒烘丝干燥过程中采集了大量热工数据,但各数据(热风温度、蒸汽压力、物料流量等)量纲差异较大,对模型收敛速度和复杂度有重要影响,需对数据进行归一化消除量纲影响。
根据1.2节所述的mRMR算法,计算各输入变量与区域1筒壁温度之间的互信息值,见表3。采用mRMR算法后,与区域1滚筒温度密切相关的变量排序为X8,X2,X9,X3,X5,X6,X7,X11,X13,X10,X4,X12,X1。综合现场专家知识和实践经验,最终选取区域1冷凝水温度(X8)、入口物料含水率(X2)、HT蒸汽压力(X3)、入口实际水分(X6)、工作蒸汽压力(X7)、热风温度(X11) 6个变量作为软测量模型最佳输入。
烘丝机干燥过程是个大滞后的非线性动态系统,为了实现筒壁温度的准确预测,需考虑输入与输出变量的时序及时滞关系[15-16],故建立非线性动态映射关系如下:
Y(t)=fDGRU{X(t),X(t-1),X(t-2)}
其中,延迟时间为2个时刻,代表将当前采样时刻和前2个时刻的输入变量作为动态模型的综合输入。

表2 DGRU算法模型参数Table 2 Model parameters of DGRU algorithm
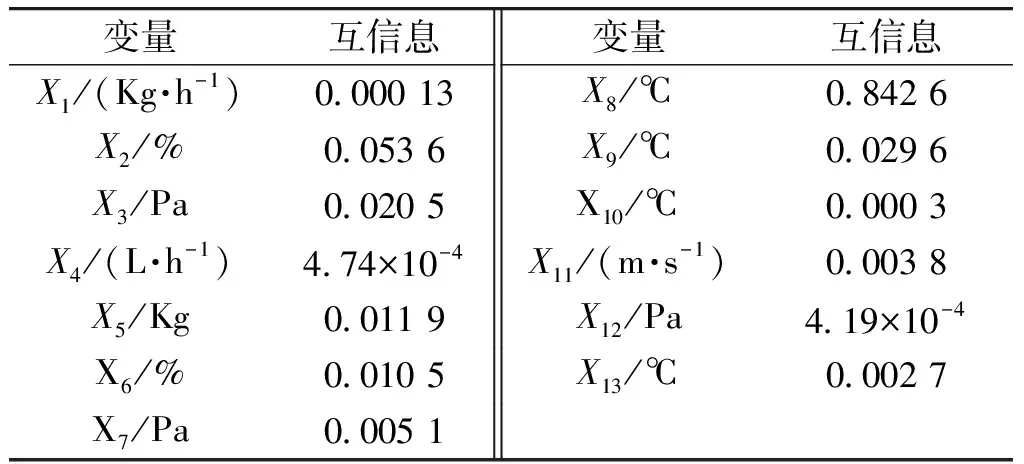
表3 输入与输出变量之间的互信息值Table 3 Mutual information between input and output variables
为客观评价模型性能,采用均方根误差 (Root Mean Square Error,RMSE)、平均绝对误差 (Mean Absolute Error,MAE)和相关系数(Correlation Coefficient,CC)3个评价指标:
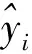
3.2 实验结果分析
4种算法下筒壁温度预测的对比结果见表4。为了更直观地显示算法预测效果,选取测试集2的烘丝机筒壁温度的预测值和真实值结果作图,其对比曲线详见图4。
由表4可知,在3组测试集上,ELM网络的整体评价指标最差,结合图4发现ELM预测曲线与真实值具有较大偏差,说明静态网络无法捕捉烘丝干燥过程的动态特性。而采用RNN和GRU动态递归网络算法,其评价指标和预测性能均得到明显改善,这表明递归神经网络能够有效捕捉烘丝过程的动态时序特性,但单层RNN和GRU属于浅层网络,泛化能力有限,其预测性能不高。本文所提DGRU算法具有最小的RMSE和MAE,以及最大的CC,进一步由图4可知,基于DGRU的筒壁温度预测值相比其他方法能够更好地拟合真实值的变化趋势,模型输出值与实际值拟合较好,绝大多数误差控制在0.1范围内,能实现较高的预测精度。
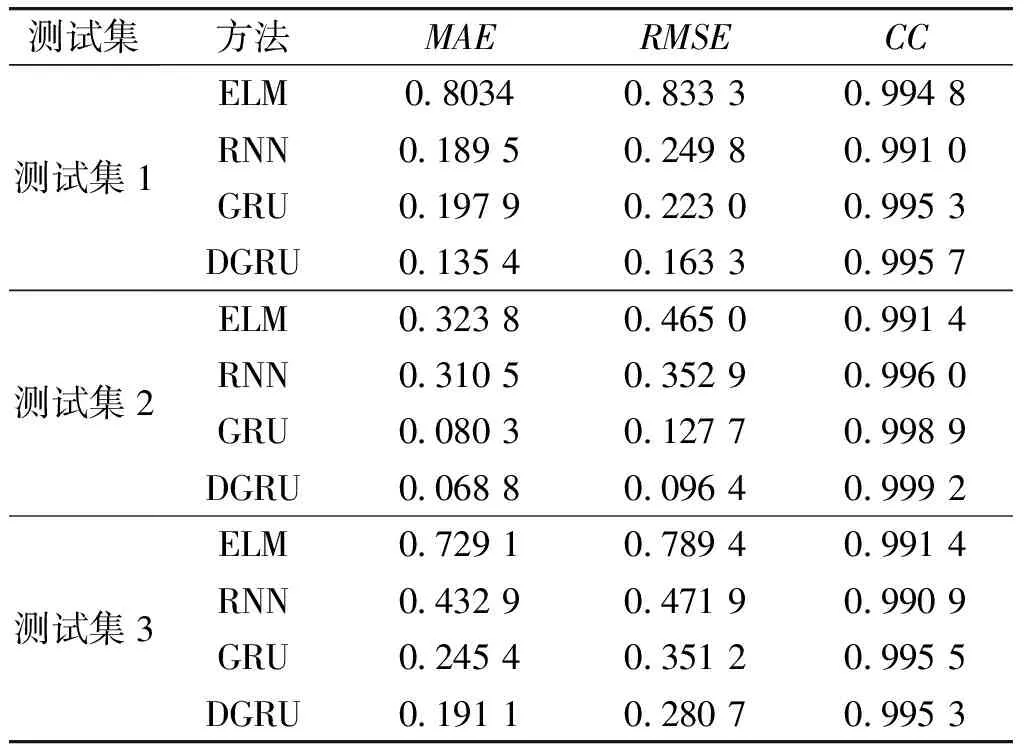
表4 4种算法下筒壁温度预测的结果对比Table 4 Quantitative comparison of cylinder wall temperature prediction by four methods
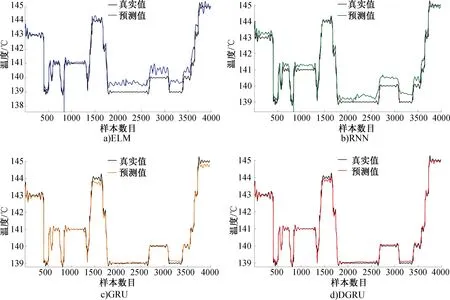
图4 4种算法下筒壁温度预测值和真实值对比曲线Fig.4 Comparison between predictive and actual curves of cylinder wall temperature by four different methods
此外,测试集2在4种算法下的预测误差箱体图如图5所示。由图5可以清晰看到ELM和RNN算法的误差中值及均值距离零刻度线有不同程度的偏离,GRU和DGRU的误差中值及均值非常接近零刻度线,其中DGRU算法造成的异常点更少,表明其具备更佳的平均预测准确度。基于DGRU算法的筒壁温度相关系数如图6所示。由图6可知,筒壁温度预测值和真实值趋势一致,预测较准确。
4 结论
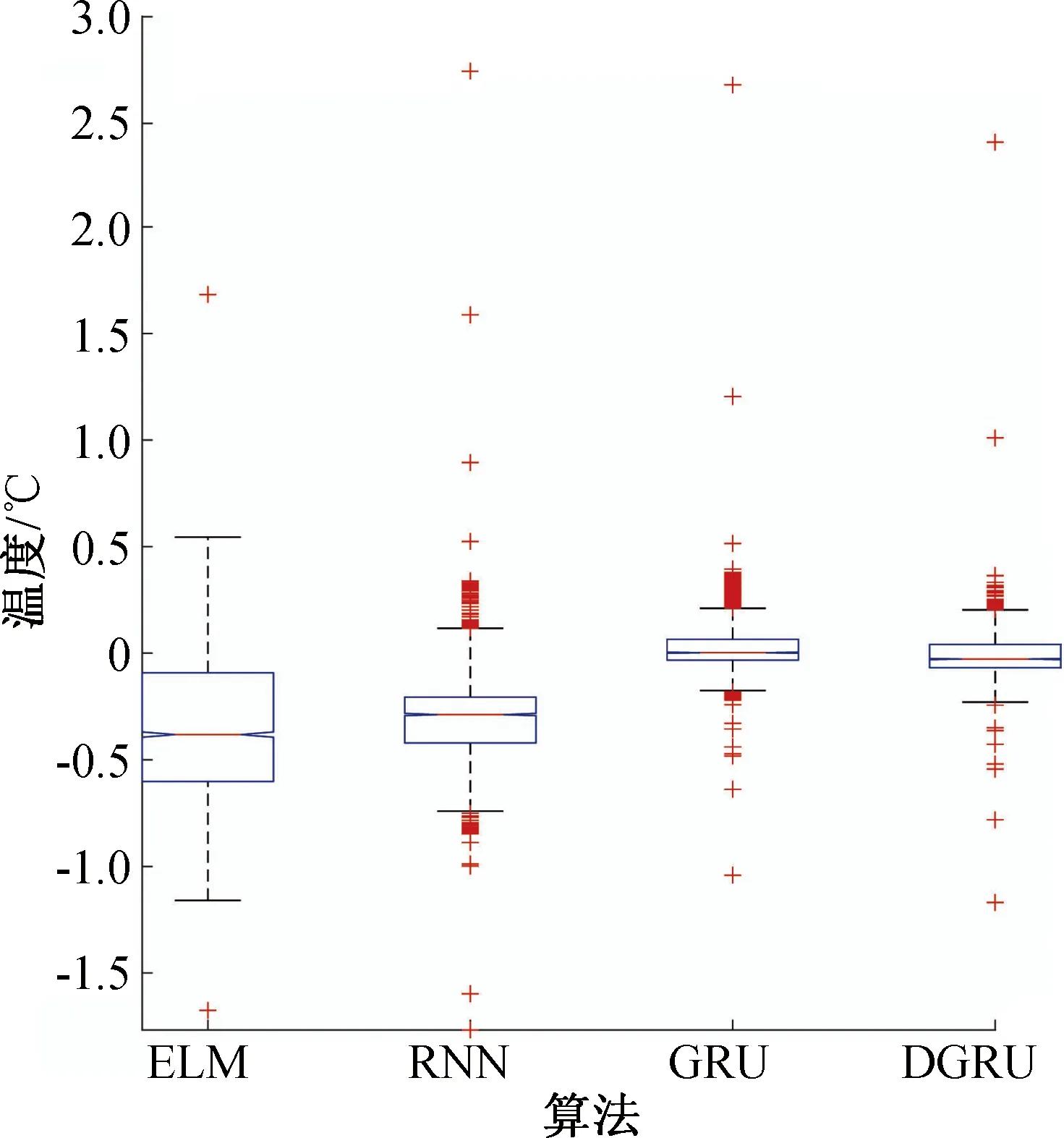
图5 4种算法下的预测误差箱体图Fig.5 Prediction error boxplot by four different methods
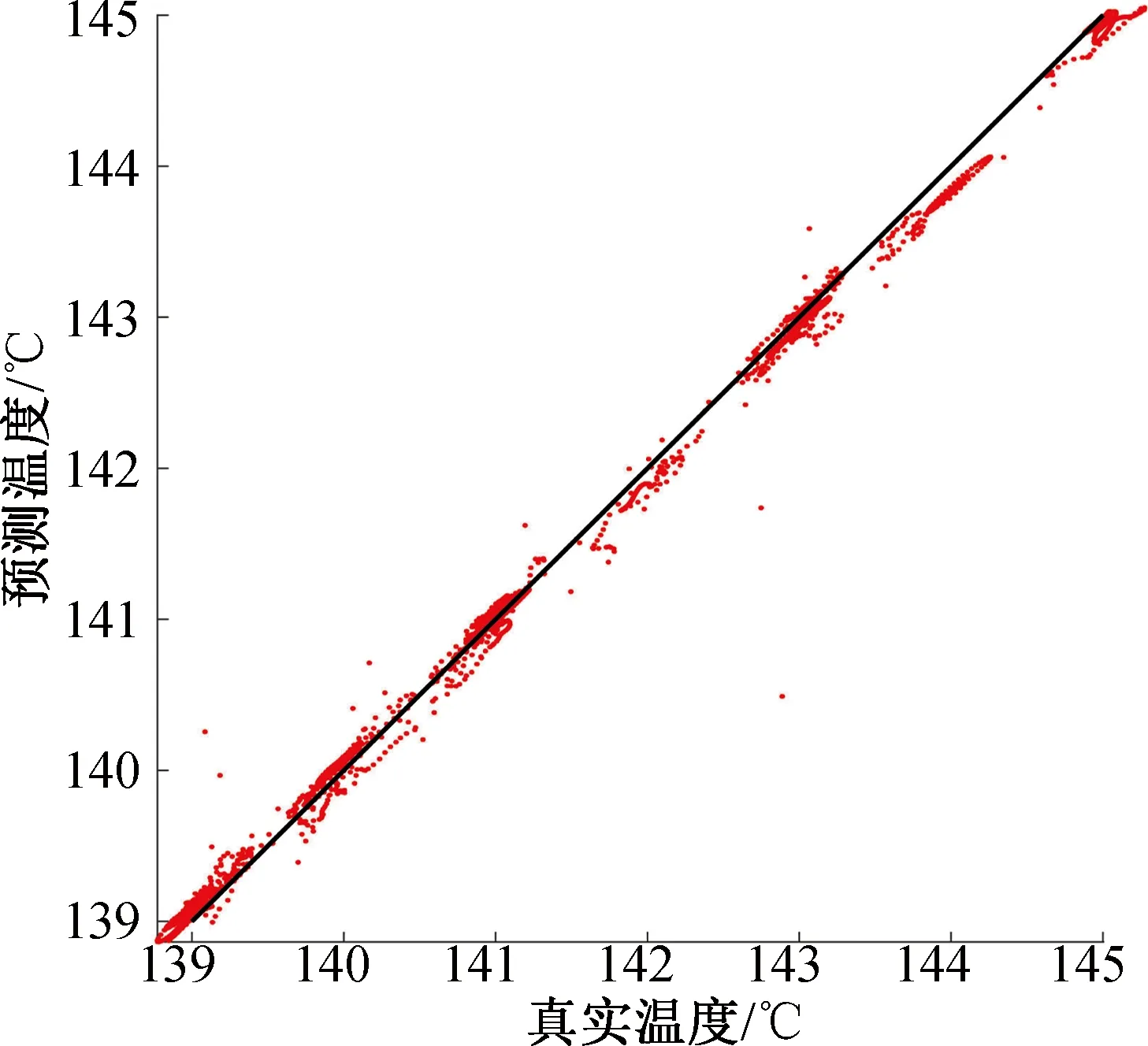
图6 基于DGRU算法的筒壁温度相关系数Fig.6 Correlation coefficient of cylinder wall temperature by DGRU method
针对烘丝机筒壁温度难以准确进行在线检测的问题,本文提出了基于DGRU的筒壁温度动态预测方法,为烘丝机筒壁温度在线检测提供了新的技术手段。该方法先对现场工业数据进行小波去噪、归一化等预处理操作;然后采用最大相关最小冗余选取与筒壁温度相关性最大的输入变量,简化模型复杂度,提高模型性能;最后利用堆叠GRU网络和全连接层的深度学习方法预测在线温度。基于烟厂实际烘丝数据,实验结果表明DGRU算法造成的异常点较少,预测值和真实值趋势一致,在预测准确性方面明显优于传统算法,能够提高筒体壁温度预测精度。在未来研究工作中,可重点研究注意力机制方法,以进一步提高模型预测精度。
