基于三通道融合的结构光中心条纹提取算法

周国平， 陈 聪， 肖可洋， 彭金华， 赵 艳， 祝振敏*

(1.江西省水利水电开发有限公司，江西 南昌 330029； 2.华东交通大学 电气与自动化工程学院，江西 南昌 330013)

大坝形变测量是衡量大坝是否正常和运行安全的重要标志,为大坝的安全维护和运行提供了可靠的依据[1]。结构光测量能够高效率、高精度采集大坝形变测量的数据，满足形变监测，达到各项指标的要求[2]。其通过在目标物体上自动投影光带，有利于特征点的提取和匹配。但是光条有一定的宽度，特征点可以用中心线更精确地表示。因此，对结构光中心条纹的提取是关键的一步。Perona等[3]提出了一种极值法，选择条纹横截面上灰度值最大的像素作为中心，这种方法虽然简单高效，但只能提取像素级的条纹中心线，对噪声敏感。文献[4]提出的方向模板法和改进方向模板法可以有效地抑制噪声，提取像素级的中心点，但由于互相关的存在，该方法的计算量较大。Sun等[5]提出了一种基于灰度矩阵和光滑样条算法的鲁棒中心提取算法，该算法基于条纹光强均匀分布的假设，但大多数激光器遵循高斯分布[6]。Goshtasby等[7]提出了一种基于高斯算子的拉普拉斯曲线拟合方法来检测激光条纹中心，该方法假设条纹截面上的灰度值分布是对称的，实际上，灰度分布通常是非对称的。为了获得更高的精度，亚像素中心提取方法受到越来越多的关注。最经典的方法之一是Steger算法[8]，其最初是为医学成像而设计的，但由于其具有高鲁棒性和高精度的优点，该方法逐渐成为激光条纹提取的常用方法之一[9]。在中心提取过程中，光条图像中的所有像素都需要进行5次高斯卷积运算。为了在亚像素级提取中心点，需要求解Hessian矩阵的特征值和特征向量[10]。这个过程包含大量的计算，因此非常耗时。此外，很难确定条纹的第1点。Liu等[11]提出的图像处理单元(Graphics Processing Unit,GPU)和江洁等[12]提出的可编程逻辑门序列(Field Programmable Gate Array,FPGA)方法也是以减少计算时间为目标。然而，由于Steger算法高度依赖于这些算法中参数的设置，例如高斯核的标准差和特征值阈值[13]，因此，具有固定值参数的Steger算法不适用于不同宽度和噪声幅度的光条。蔡怀宇等[14]提出了一种利用主成分分析估计条纹法线方向的方法，然后利用二阶泰勒展开得到中心点的亚像素位置。这种方法也是基于高斯卷积运算，所以计算成本也比较高。Li等[15]提出了一种改进的灰度重心法，用于亚像素级提取激光条纹中心。针对上述问题，本文提出了一种三通道特征融合算法来提取条纹中心点。首先分别在Gabor、局部二值模式(Local Binary Patterns,LBP)以及方向梯度直方图(Histogram of Oriented Gradient,HOG)这3种特征描述因子下得到光条纹的3种特征图像，并融合这3种特征图像以得到最终的光条纹特征图像。最后对分割出的光条纹中存在的不连续区域进行灰度膨胀并通过骨架细化法得到光条纹的中心线，将其映射到原始的结构光条纹图像上。

1 三通道特征提取图像融合

Gabor小波可以在不同方向和尺度上提取图像的纹理信息。HOG特征中包含的边缘梯度和方向密度可以表示浅色条纹的外观和形状。LBP用来描述物体局部纹理特征的算子形象，因具有旋转不变性和灰度不变性，在描述图像局部纹理特征方面具有一定的优势。

本文方法提出的三通道融合是指利用Gabor、LBP、HOG得到3幅光条特征图像，并将这3种特征图像定义为I_Gabor、I_HOG和I_LBP，融合这3种特征图像可以得到最终的光条纹特征图像I_final。最后对分割出的光条纹中存在的不连续区域进行灰度膨胀并通过骨架细化法得到光条纹的中心线，将其映射到原始的结构光条纹图像上。

1.1 Gabor光条特征提取

本文方法采用二维Gabor滤波器来完成第1通道特征提取。二维Gabor函数是由具有一定频率和方向的正弦平面波组成的复正弦函数，然后被二维高斯函数调制。二维高斯函数为

(1)

式中:a、b、σx、σy和ρ均为常数，a、b分别为随机变量x和y的均值，σx和σy为两者的方差，ρ为两者之间的相关系数，并设a、b和ρ等于零。所以，式(1)可转化为式(2)。因此，二维Gabor函数的复数形式可以表示为式(3)。它的实部和虚部可以用式(4)表示。在式(4)中，λ为余弦因子的波长；θ为平行条纹的方向Gabor函数；ψ为相移；γ为空间长宽比，决定椭圆度对于Gabor函数的形状；σ决定了高斯窗口宽度与高斯窗口宽度的比值波矢的长度。Gabor滤波器的半响应空间带宽滤波器与σ/λ之比有关，可用式(5)来表示。Gabor滤波器的实部是一个偶对称滤波器，满足由Rivera等[17]提出的要求，用其来获取光条纹的特征。对于不同的带宽和标准差得到的结构光条纹特征图像会有所不同，因此本文方法选取了几组不同的σ取值和d取值，得到对应的特征提取效果，如图1所示。

(2)

(3)

(4)

(5)

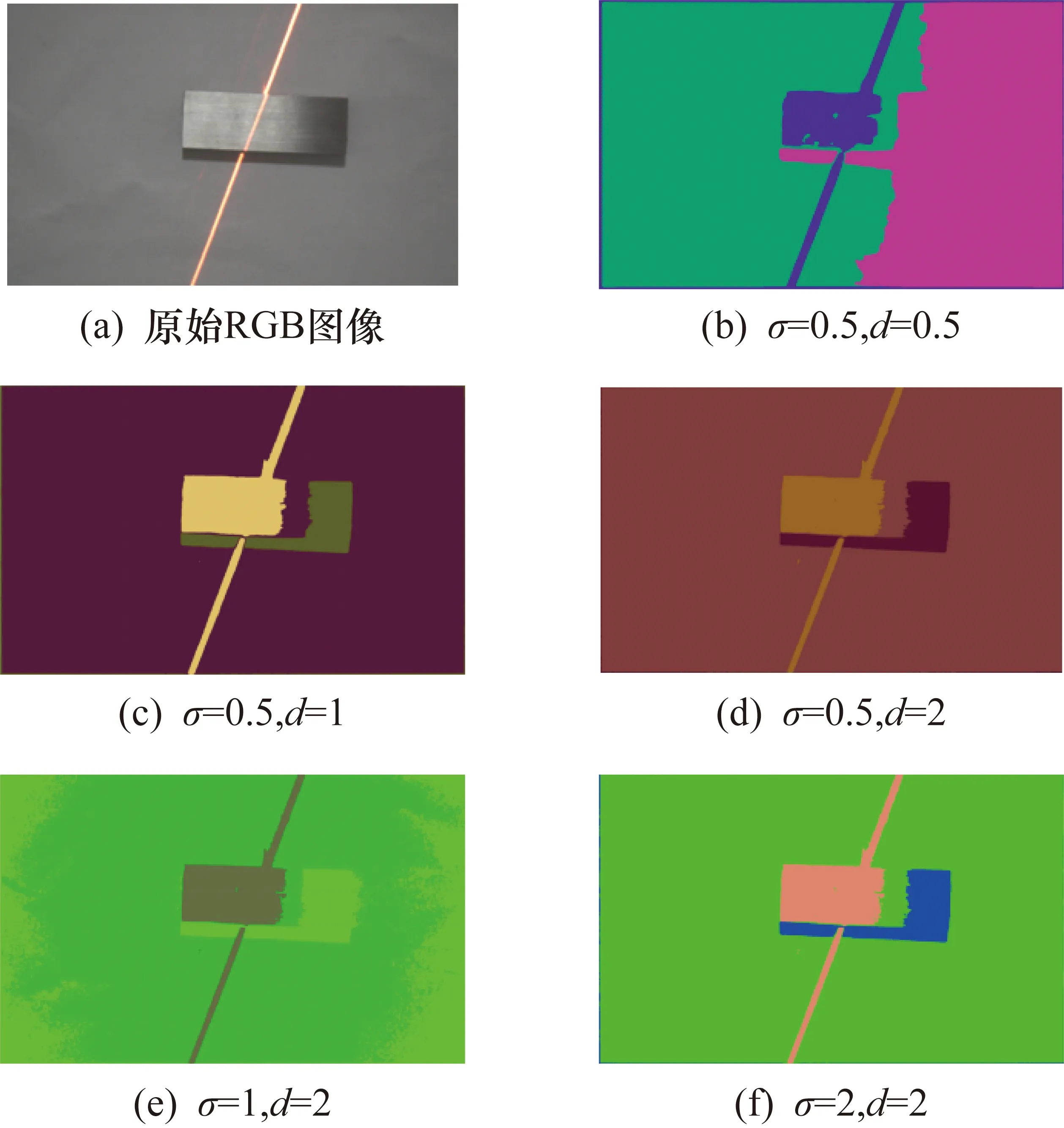
图1 基于σ和b的不同的特征提取

图1(a)为采集到的原始结构光条纹图像，对应于不同σ和d的组合，分别可得图1(b)～图1(f)这5种不同的条纹提取效果。由于d取值通常以1个倍频为基础，因此可简化处理为1，同时与σ的比值为0.56。通过Gabor特征提取本文得到了光条纹的第1种特征图像I_Gabor。

1.2 HOG光条特征提取

HOG特征中包含的边缘梯度和方向密度可以表示浅色条纹的外观和形状。条纹中像素(x,y)的梯度可以用式(6)表示。

(6)

式中：Gx(x,y)和Gy(x,y)为像素在水平和垂直方上的梯度方向；I(x,y)为这些像素的灰度值，其梯度大小和方向如式(7)所示。

(7)

为了减弱光和噪声的影响，需要对原始结构光条纹图像进行处理，首先通过式(8)所示的伽马压缩进行归一化。在本文方法中，gamma=0.5。

Ig(x,y)=I(x,y)gamma

(8)

式中：Ig(x,y)为压缩图像。本文方法拍摄的结构光条纹图像尺寸为1200像素×1920像素。首先，8像素×8像素被定义为一个单元。然后将梯度方向划分为9个单元。这个梯度方向只能确定像素所属的仓，梯度大小可以确定此箱子中此像素的计数。通过加权每个像素可以得到方向梯度直方图，如式(9)所示。

(9)

式中：Num为每个单元格中对应于像素的梯度方向特征的计数。将2×2单元定义为块，并使用8像素作为步骤的滑动窗口扫描光条纹图像。在每个块中，都可以得到它的HOG特性。将这些块连接在一起，解决了整个图像的特征。基于HOG的特征提取如图2所示。

图2 基于HOG的特征提取

此时，将结构光的第2通道特征图像定义为IHOG。

1.3 LBP光条特征提取

LBP用来描述物体局部纹理特征的算子形象，具有灰度不变性和旋转特性。在一个3像素×3像素的正方形窗口中定义原始LBP算子，并将其灰度值相邻像素与窗口的中心像素进行比较。这个固定的区域大小LBP无法适应目标图像大小的变化。为此，笔者采用了一种非固定区域的圆形LBP算子。图3为3种不同的LBP环。

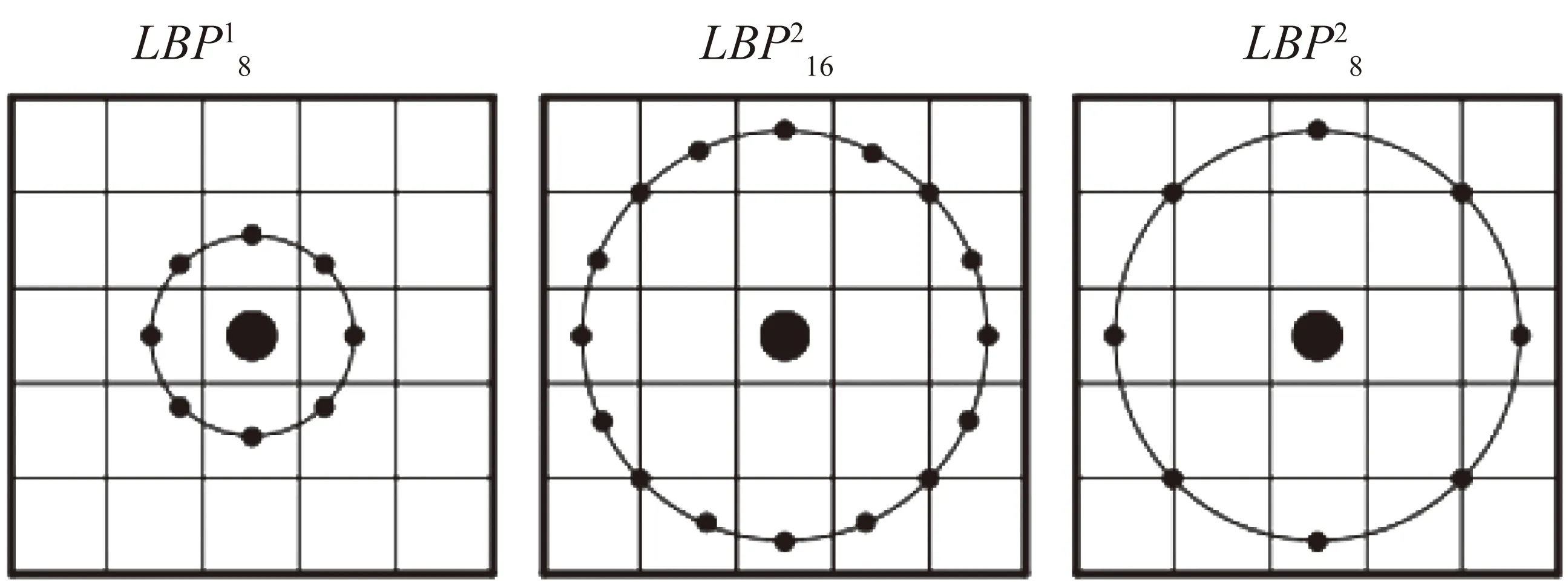
图3 3种不同的LBP环

图3中，从左到右是采样半径和采样次数不同的LBP算子样品。变半径LBP算子能较好地满足纹理特征结构光条纹图像的不同大小和频率。对于给定的中心点(xc，yc)，圆形区域中第p个像素的坐标为

(10)

式中：R为采样半径;p为采样点;P为采样点总的个数。对于计算出的非整数像素值，采用插值的方法计算整数插值点来表示。考虑到最初的LBP特征，利用圆形LBP算子提取结构光条纹。提取效果如图4所示。

图4 基于LBP的特征提取

此时，将第3通道特征图像定义为ILBP。

1.4 三通道特征融合图像

三通道特征图像用于获得最终的光条纹特征。融合过程为

Ifinal=ω1·IHOG+ω2·IGabor+ω3·ILBP

(11)

式(11)表达了三通道图像之间的关系，其中ω1=ω2=ω3=1，三通道特征融合过程如图5所示。

图5 三通道特征融合过程

为了从背景中分割出结构光条纹，首先进行像素增强。其次，考虑图像中的像素强度光条纹面积较大，通过多次实验，80%的最大灰度值为从背景中分割光条纹的阈值。但是，不连续区域将出现在分段条纹中。为此，应用灰度展开算法来填充这些不连续的区域；然后采用骨架细化法，得到目标的中心线条纹并将其映射到原始的结构光图像，如图6所示。

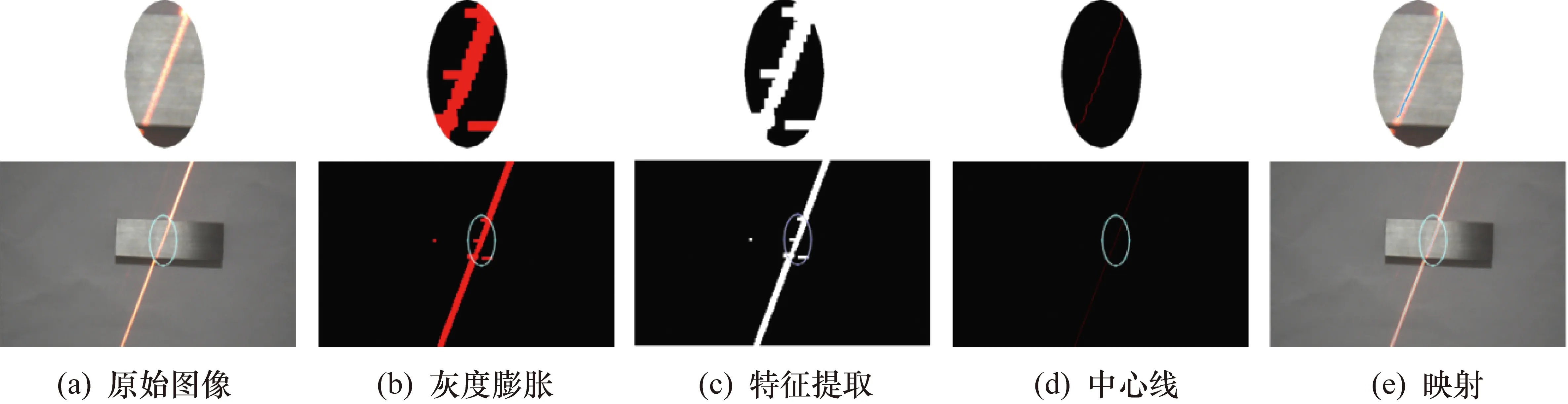
图6 光带中心线提取过程

2 光条纹中心提取

结构光条纹中心的提取技术分为两类：基于几何中心的方法和基于能量中心的方法。因为几何中心法对噪声敏感，所以该技术对光条纹的质量要求高。由于没有考虑光条的能量分布，因此应用范围有限。本文方法采用了基于Hessian矩阵的Steger算法来提取条纹中心，使得条纹边缘检测精度能够达到亚像素级。Steger算法的实质是求解光条纹区域中每个像素的Hessian矩阵。首先，在Hessian矩阵中求解条纹区域中每个像素的法线方向，然后在法线方向上的Taylor展开可以表示这些像素的子像素位置坐标。任意像素(x,y)的Hessian矩阵可表示为

(12)

式中:H(I(x,y))为条纹区域中每个像素的Hessian矩阵；rxx，ryy，rxy分别为二阶偏导数。在Hessian矩阵中，绝对值最大的特征值代表灰度图像的二阶导数。其特征向量决定了光条的法线方向(nx,ny)。通过求解Hessian矩阵，结合光条的基准点，中心点计算公式为

(13)

当(anx,any)∈[-0.5,0.5]×[-0.5,0.5]时，可以确定第1个等于零的导数处于正在操作的像素内。同时，如果对应于线方向(nx,ny)的二阶方向导数大于给定的阈值，可由该阈值推导出中心点的亚像素坐标(xc,yc)。

3 实验设计与验证

笔者采取3个实验模块来验证本文方法，分别是提取的光条平滑度分析、工件表面三维重建和工件尺寸测量。

3.1 实验设计

首先采用双目视觉系统验证光条中心提取算法。由于左右图像的特征匹配是完成三维立体重建的必要步骤，其精度直接影响重建和尺寸测量的结果，而传统的特征点匹配技术应用于传统的立体测量技术中，与目标物体的表面纹理关系密切，受环境光的影响较大。与传统的立体测量技术不同，在结构光视觉测量系统中，结构光条纹上的中心点是特征点。因此，随着特征点定位精度的提高，可以更好地完成工件的三维重建和尺寸测量。本实验分析了基于SIFT特征匹配算法的三维重建效果和双目视觉系统中的结构光中心点匹配。利用匹配结果，可以得到两幅视差图，并结合双目摄像机的内外参数重建工件表面。双目视觉测量系统如图7所示。

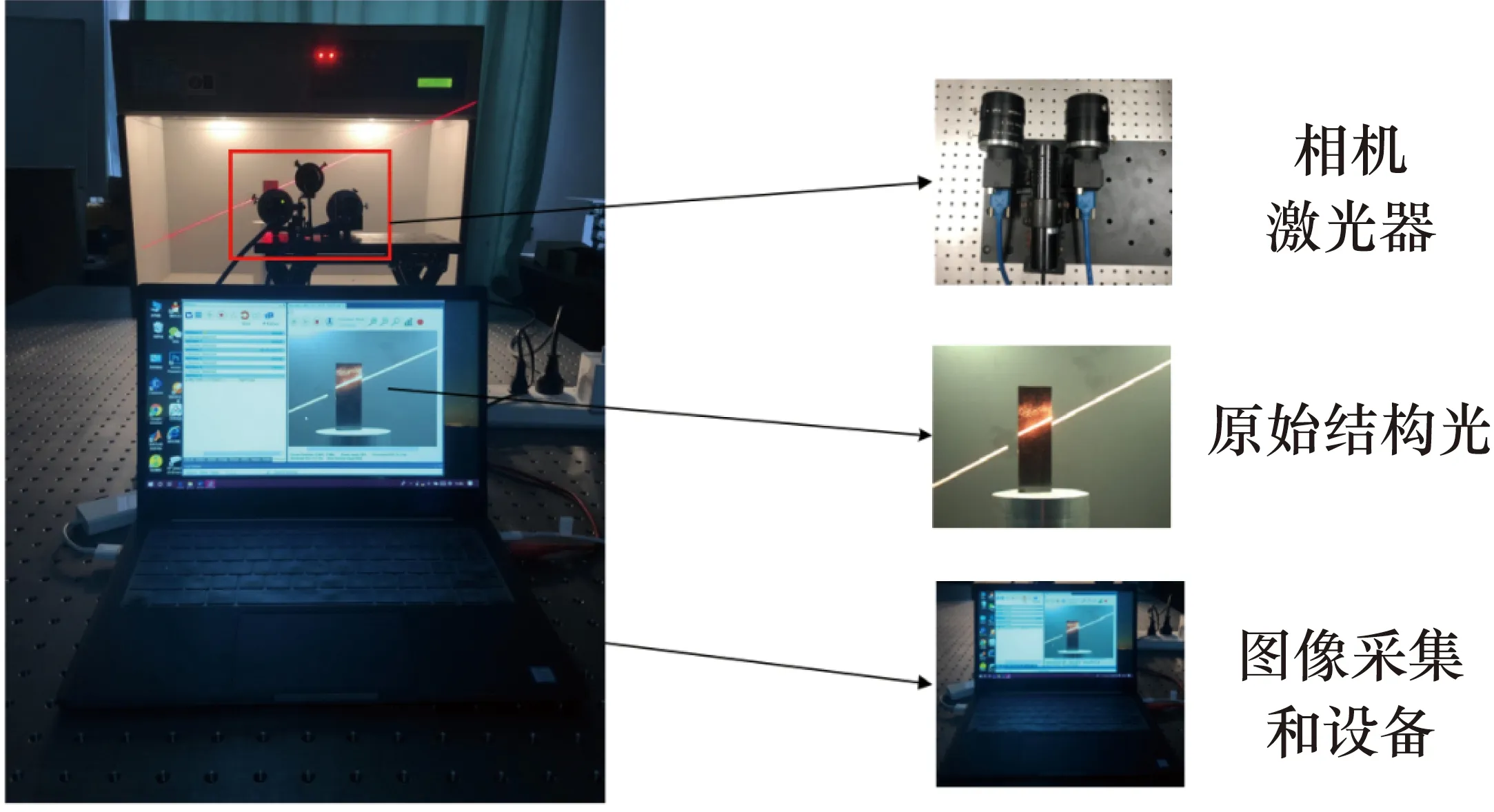
图7 双目视觉测量系统

一个激光器和两个摄像头组成了一个基础的双目视觉系统。通过打开和关闭激光器，左右摄像头可以捕捉带有或不带有结构光条纹的工件图像。在式(14)中表示了图像像素坐标(u,v)及其空间三维坐标(XW,YW,ZW)的映射函数。

(14)

式中:R3×3为旋转矩阵;T3×1为平移矩阵;bx和by分别为水平和垂直方向上的成像焦距;(u0,v0)为相机中心坐标点。本文方法采用张氏标定法计算摄像机参数。在没有结构光条纹的左右图像中，使用SIFT算法进行立体匹配,得到匹配结果，如图8所示。

图8 基于SIFT的特征点匹配

由图8可以看出，前景区域和背景区域之间出现了特征点不匹配，会影响三维重建和尺寸测量。结构光技术的优点是可以准确定位特征点，从而减少特征点匹配的误差。与SIFT算法相比，该方法的结构光中心点匹配的准确率更高，如图9所示。

图9 结构光中心点匹配

对比图8和图9，结果表明结构光中心点的匹配效果更好。根据匹配的结果能得到工件图像的视差图，可用于工件表面重建。基于SIFT的工件表面的三维重建效果如图10所示。图10中，O-xyz为世界坐标系。

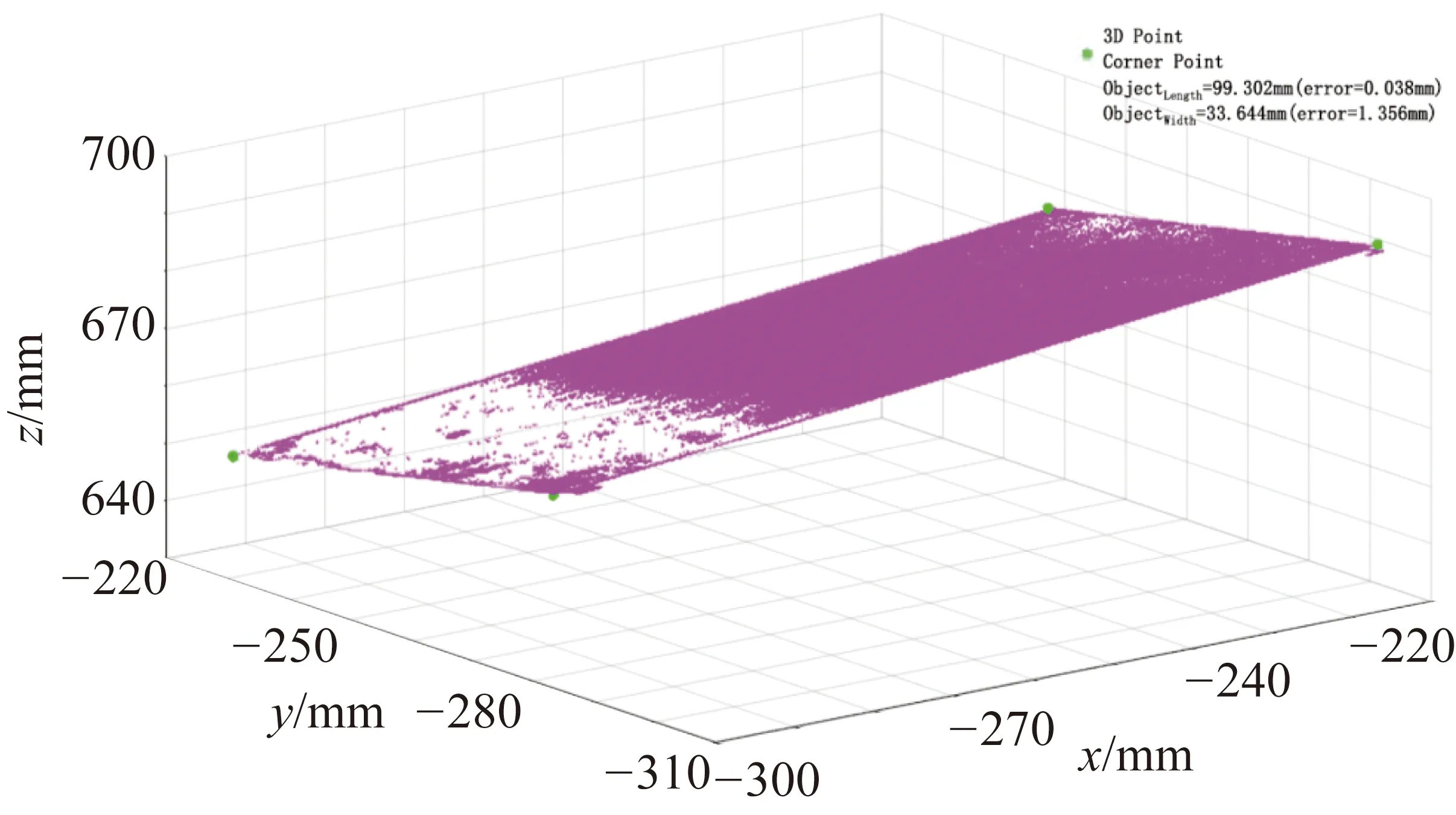
图10 基于SIFT的工件表面三维重建效果图

为了验证结构光技术的优点，进行了基于SIFT的工件表面三维重构和基于光技术的工件表面三维重构两个实验。在图10中，小区域中的3D点相对稀疏。这是SIFT算法的不匹配和工件表面纹理信息不足造成的。

结构光技术通过在工件表面主动投射激光条纹可以获得更多的特征点信息，其三维重建效果如图11所示。与图10相比，在传统的双目视觉系统中引入结构光后，工件表面重建的三维点在同一区域明显增加。

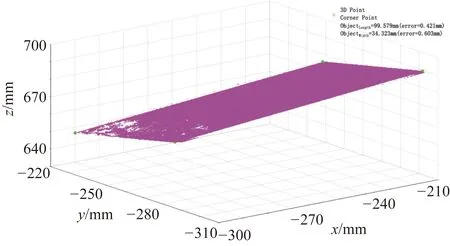
图11 基于结构光技术的工件表面三维重建效果图

3.2 实验分析

在该实验中，中心线上相邻像素的列坐标之间的差异被用作评估提取的线结构光的平滑度的基础。图12展示了本文算法和传统Steger算法的结果及其局部放大图像的对比。

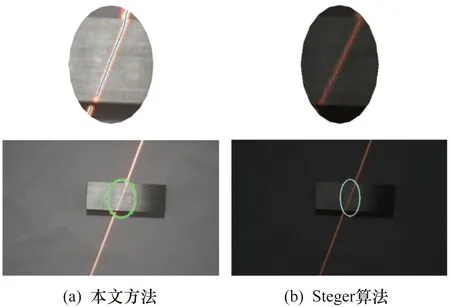
图12 基于两种方法的光条中心线

由于工件表面光滑，线结构光中心点之间的柱坐标差可以作为评价提取结果的标准，如表1所示。

表1 线结构光中心点之间的柱坐标差

对表1的分析表明，相比于Steger算法，本文方法的最大列坐标差为2像素，平均列坐标差为0.069像素，相较于Steger算法的9像素和0.196像素，具有明显的提升。为了进一步阐述本文方法的优势，采用以上两种方法测量工件尺寸。

3.3 实验验证

为了比较Steger算法和本文方法提取光条中心的准确性，将使用这两种方法来完成工件的尺寸测量，标准尺寸为35 mm×100 mm。在本实验中，为了全面评估测量精度，图7中工件的长边和短边都将是测量的目标。首先，通过三维重建的结果得到结构光双目视觉测量系统中每条边上的点。表2和表3展示了工件长边对应的测量尺寸。分别计算左、右边界上的点到左、右拟合边的距离。

利用本文方法测量的长边尺寸结果如表2所示。根据表2，左侧点与拟合的右边缘之间的平均距离为100.124 mm。类似地，右侧点与拟合的左边缘之间的平均距离为100.133 mm。根据两次测量结果，长边的尺寸为100.127 mm。同理，如表3所示，利用Steger算法测量的长边尺寸为100.210 mm。与工件标准尺寸相比，本文方法的测量精度为0.127 mm，Steger为0.210 mm。

表4和表5展示了工件短边对应的测量距离。利用本文方法，上边缘的点到下边界的直线距离为34.898 mm，下边缘的点到上边界的直线距离为34.899 mm。因此使用本文方法测量短边的精度为0.101 mm。同理，使用Steger算法得到短边的测量精度为0.185 mm。

两种方法的测量精度分析如表6所示。本文方法对工件尺寸的平均测量精度为0.114 mm，相较于Steger方法的0.197 mm，有着较为明显的提升。综上所述，本文方法不仅能够更好地重构工件表面，而且在尺寸测量方面也比Steger具有更高的精度。

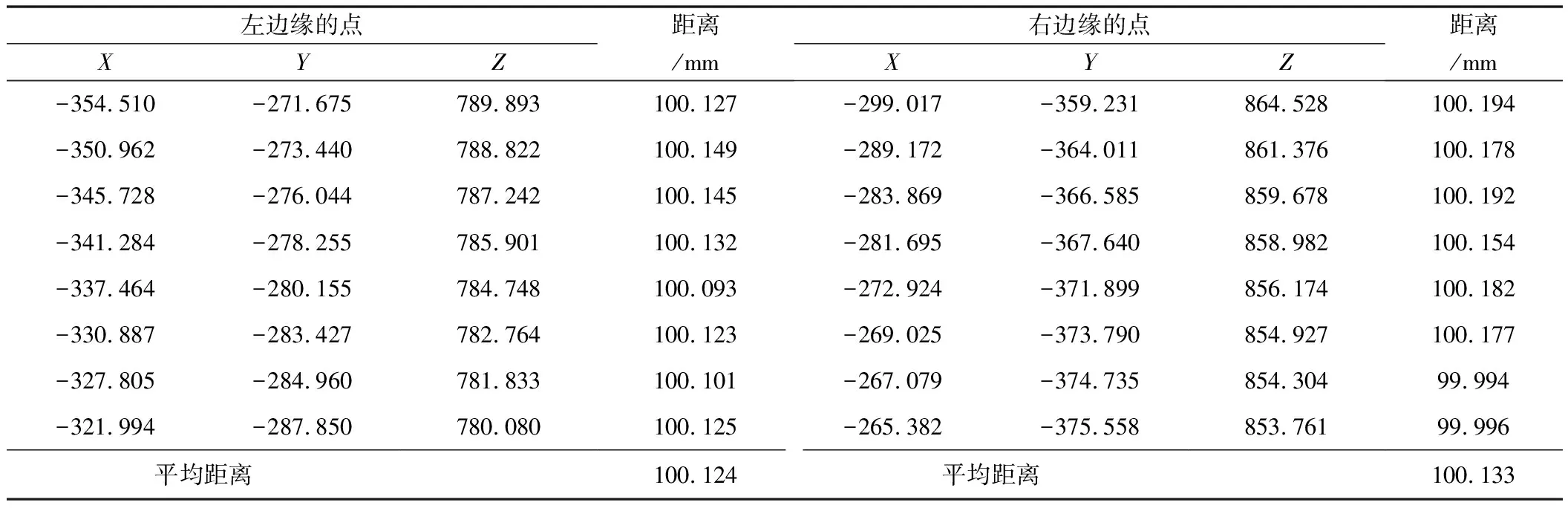
表2 基于本文方法的长边尺寸

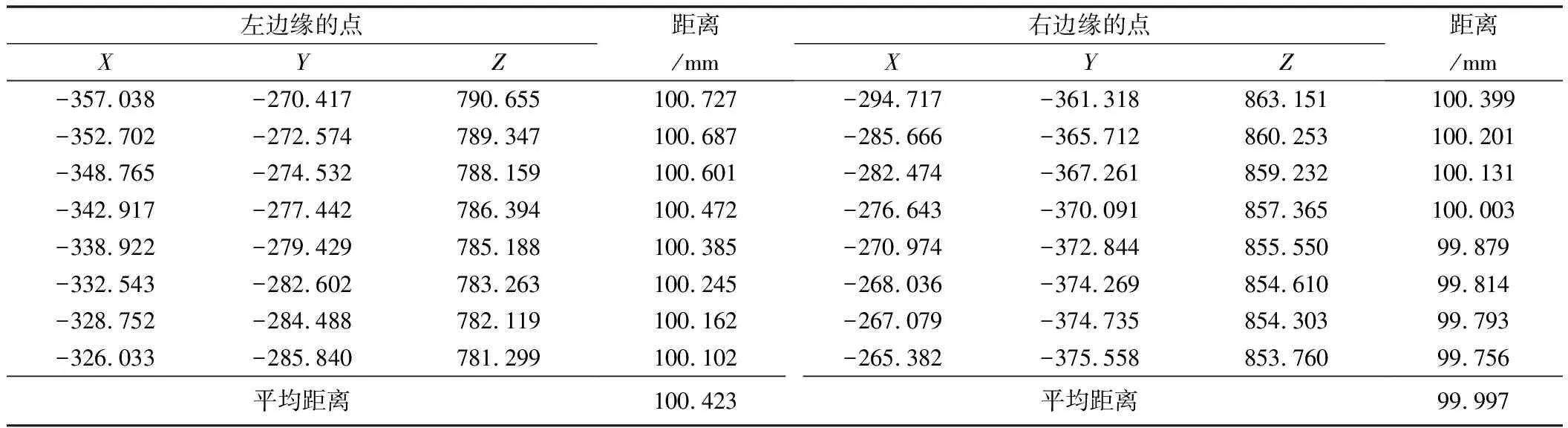
表3 基于Steger的长边尺寸

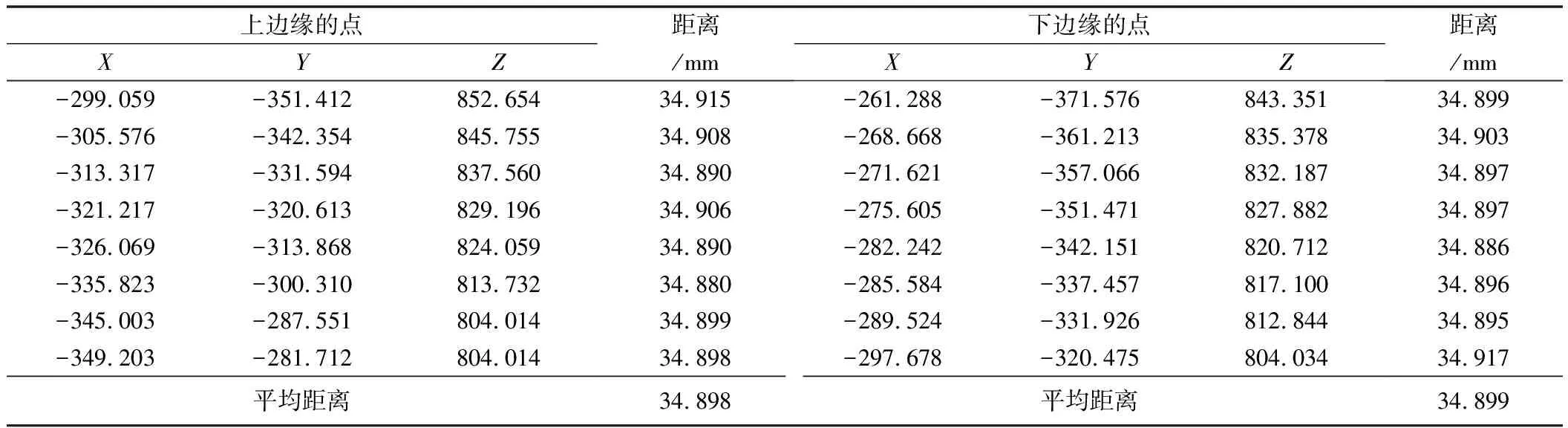
表4 基于本文方法的短边尺寸

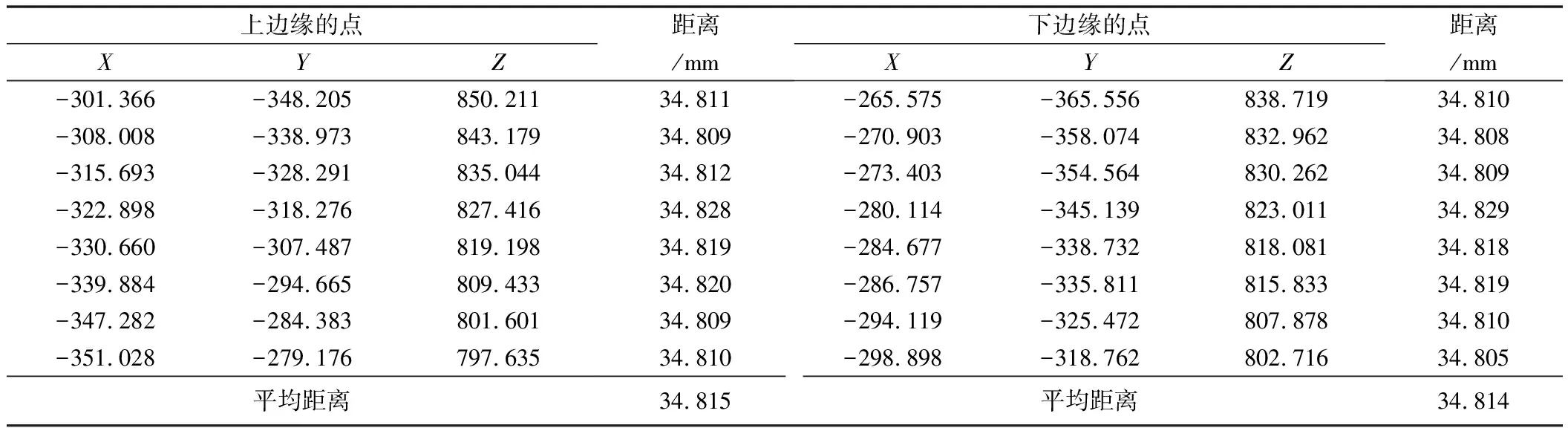
表5 基于Steger的短边尺寸

表6 两种方法的测量精度分析

4 结束语

坝体形貌测量常会遇到图像噪声等问题，在视觉测量过程中，这些问题会降低光条中心的提取精度。针对上述问题，首先，引入三通道特征融合方法以提取光条，然后，利用灰度扩展算法和细化骨架方法计算左右光条图像的中心线。为了验证该方法在表面三维重建和工件尺寸测量方面的优势，进行了提取光条平滑度的分析、工件表面三维重建和工件尺寸测量3个实验。首先，在传统的双目视觉系统中，引入结构光前后，工件表面重建的三维点明显增加。然后，在工件表面三维重建和工件尺寸测量中，列坐标首先比较线结构之间的差异，以证明本文方法的优点。该方法的最大和平均列坐标差分别为2像素和0.069像素，Steger分别为9像素和0.196像素，为了进一步验证该方法的优势，将工件的标准尺寸(35 mm×100 mm)与两种方法测量的尺寸进行了比较。实验结果表明，长边和短边的测量精度分别为0.127 mm和0.101 mm，Steger测量的长边和短边的精度分别为0.210 mm和0.185 mm，综合考虑长边和短边的测量精度为0.114 mm,高于Steger的0.197 mm。经过上述研究，运用本文方法进行坝体视觉测量的鲁棒性和精度得到了显著的提高。