基于空气耦合超声Lamb波对铝板的特征成像检测
2022-12-07王文强王树宏徐红杰
胡 宸, 向 苹, 王文强, 王树宏, 徐红杰
(1.上海复合材料科技有限公司,上海 201112; 2.上海航天树脂基复合材料工程技术研究中心,上海 201112;3.上海航天精密机械研究所,上海 201699)
铝合金因具有高比强度和刚度及耐腐蚀性能好等优点,被广泛应用在汽车制造、高层建筑、轨道交通和航空等领域[1]。而人为不当操作以及实际使用中工作环境的复杂多变将会导致铝合金构件出现冲击损伤和疲劳裂纹等问题,从而导致严重的安全事故。无损检测技术因其无破坏性、检测全面性成为发现这些安全隐患直接而有效的手段之一[2-3]。因此,为避免安全事故的产生,寻求一种有效的无损检测方法对于铝合金材料的质量评估具有重要意义。
目前,空气耦合超声Lamb波检测方法得到许多研究人员的重视。相较于传统的超声检测的逐点检测效率低下这一缺点,空气耦合超声技术不仅满足可控声束、高灵敏度、低成本等技术要求,还兼具搭建系统较为简单、不污染环境等特点,非常适合在役检测[4-6]。Liu等[7-9]采用空气耦合超声Lamb波技术结合虚拟时间反转算法实现了复合材料分层形状、大小的概率成像;基于小波变换,定义不同方向下复合材料的损伤指数并对其分层缺陷进行概率损伤成像;改进损伤成像算法,消除了不均匀概率分布,提高了检测的准确性。 Liu等[10]通过实验与仿真研究了换能器入射角对激发模态的影响,预测了空气耦合超声 Lamb 波和分层相互作用的机制。Padiyar等[11]结合空气耦合超声换能器发射和接收A0模态Lamb波以轴向与径向两种方向检测并识别管道中的夹杂物及分层缺陷。Fan等[12]采用有限元方法建立多种物理模型以评估不同空气耦合超声探头入射角度的传播与反射,验证空气耦合泄漏Lamb波检测的可能性。孟翔震等[13]利用仿真与试验相结合,验证在单侧激励情况下适合采用单一A0模态Lamb波对缺陷进行检测。李立兵等[14]通过COMSOL仿真建立Lamb波的超声场三维模型,分析并验证A0模态下的激励方式与其传播特性。王兴国等[15]用空气耦合超声对不同孔径的LY12硬铝合金中的缺陷进行检测。
针对Lamb波在铝板传播过程中由于频散及多模态之间的转换导致的信号无法识别的问题,鉴于空气耦合超声Lamb波可实现层板结构的大面积快速检测的这一特性,笔者通过空气耦合超声Lamb波采集铝板信号信息,并结合概率成像算法,将特征值元素进行全加全乘融合,实现铝板中的损伤成像。
1 铝板Lamb波
基于全局矩阵算法的Disperse 软件计算2 mm铝板的频散曲线,如图1所示。分析Lamb波在板块结构中的传播特性,获取合适的模态和激发频率。
为了简化板内声场,在恒定板内选择产生Lamb波信号的激励频率,此频率小于某些模态的截止频率。

图1 厚度为2 mm的铝板的频散曲线
由图1的频散曲线可知:当截止频率小于900 kHz时,Lamb波只存在A0 和 S0 两种模态。这是由于A0模态的离面位移较大,能使空气耦合超声探头更好地接收由板中泄漏的Lamb波信号,此外,低频的Lamb波频散相较于高频更为严重,灵敏度较低。因此选用中心频率为0.4 MHz的空气耦合超声换能器来激励Lamb波,为了获取实验所需的A0模态Lamb波,采用斜入射法用以激励相应的A0模态Lamb波,由Snell定律可得:
(1)
式中:θ1、θ2分别为探头的入射角、反射角;v1为超声波在空气中的传播速度,值为340 m/s;v2为A0模态下中心频率为0.4 MHz频率的相速度,值为2236.8 m/s。
当θ2=90°时,即在铝板内Lamb波发生全反射,此时为探头的入射角的最佳激励角度。由式(1)计算得到来激发A0模态Lamb波信号的最佳激励角为8.8°。
2 实验
2.1 实验设备及方法
实验研究对象为长200 mm、宽200 mm、厚2 mm的铝板,在铝板中心有一直径为10 mm的圆形通孔缺陷,圆孔中心距离铝板左端及上端各100 mm。选用公称频率为0.4 MHz、晶片尺寸为14 mm×20 mm的空耦纵波直探头。实验装置示意图如图2所示,包括高功率超声信号发射接收器(JPR-600C)、数据采集器(PXT-1033)、60 dB增幅的前置放大器以及带NUAT21软件的计算机。
以通孔为中心,采用一发一收的检测方式将两个空耦纵波直探头以入射角为8.8°相向摆放在待检铝板同侧,如图3所示。实验过程中进行一定的微调来激励和接收A0模态Lamb波信号。空气耦合探头的中心距离铝板表面都为5 mm,两探头中心之间的距离为106 mm。图4为采用一发一收式Lamb波铝板扫查损伤区域示意图。将两空气耦合探头沿着两个互相正交的方向对铝板进行全覆盖扫描,并收集多组Lamb波信号进行分析。

图2 实验装置示意图

图3 探头摆放方式示意图

图4 一发一收式Lamb波扫查铝板损伤区域
2.2 实验结果与分析
利用空气耦合Lamb波方法对铝板进行全覆盖扫描时,由于铝板中心通孔区域的存在,导致板内声场分布无规律,在接收信号上有一定的体现。对比铝板有缺陷与无缺陷处的接收波信号的幅值大小如图5所示。可以看出,在无损伤区域处接收的声波信号高于有损伤区域的信号幅值,这是因为通过通孔区域时声阻抗变大,Lamb波衰减较大,幅值明显降低。同时也验证了同侧相向检测法对铝板缺陷进行检测的可能性。
为了对铝板实验对象中的缺陷进行图像重现,两探头距离为106 mm,将探头沿铝板的x和y方向(即沿铝板的水平方向和垂直方向)间隔1 mm 为步进距离采集106组信号,得到一个采样范围为106 mm×106 mm的Lamb波扫描号,如图6所示,两条曲线分别为铝板x和y方向上的各个位置信号的幅值对比。从图6中可以看出,当空气耦合超声探头在无损伤区域扫查时幅值较大且基本保持一致;随着扫查距离的增大,在靠近中心损伤区域时幅值骤降且达到最低,但当扫查距离不断增加直至远离损伤区域时,接收信号幅值逐步增加并趋于恒定。结果表明,空气耦合超声Lamb波可有效识别铝板的损伤情况。
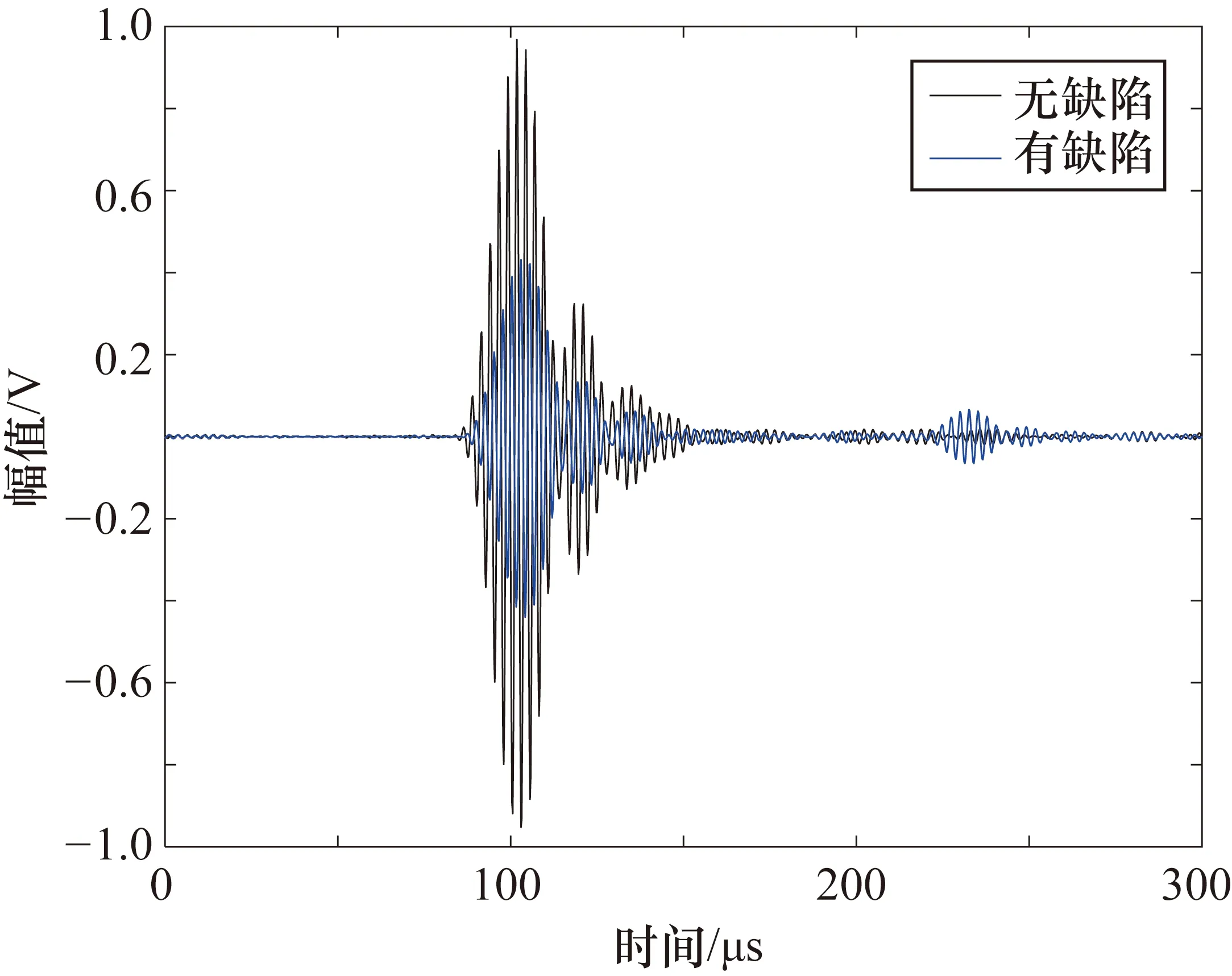
图5 有/无缺陷区域接收的Lamb波信号
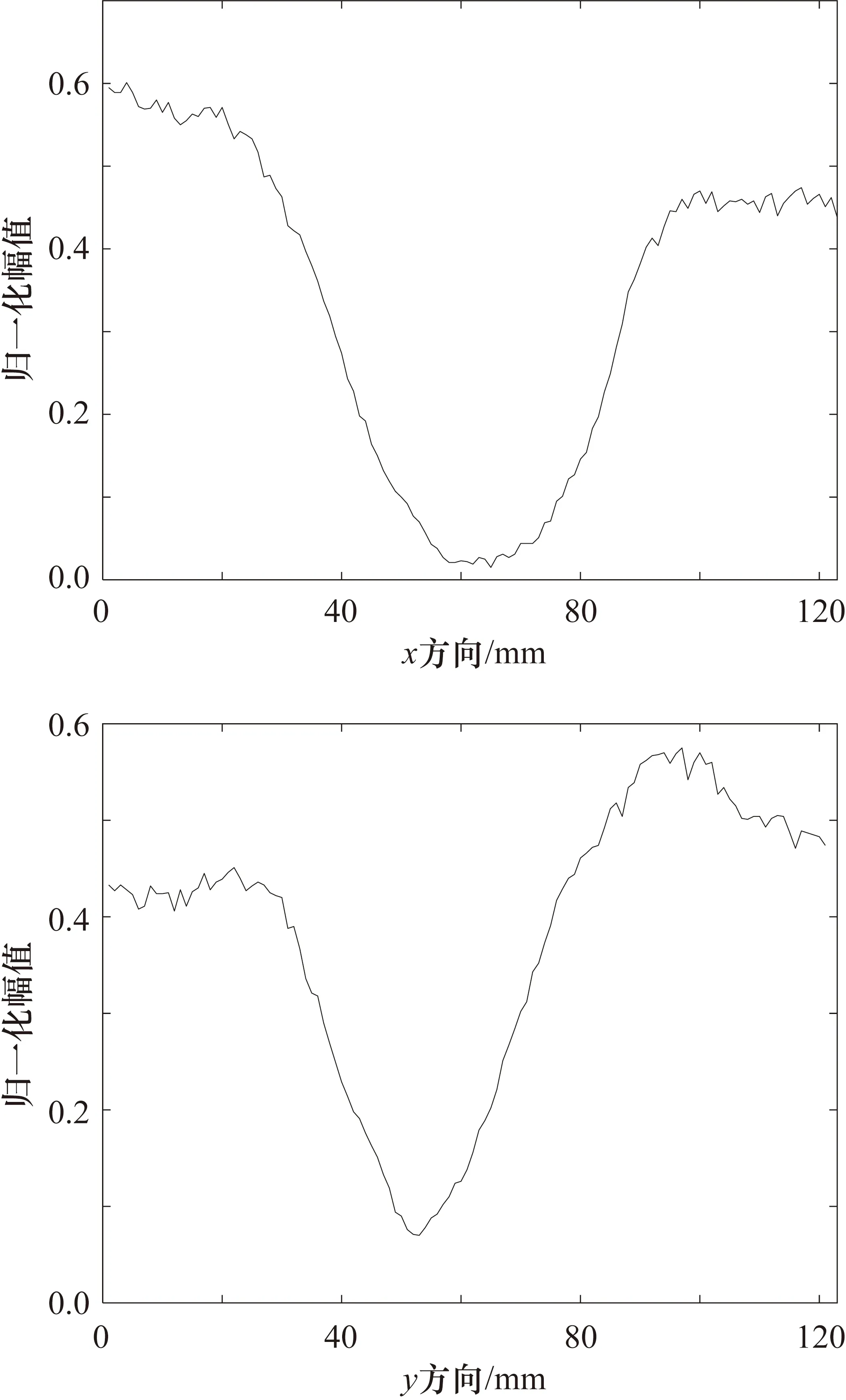
图6 铝板x、y方向上接收的Lamb波信号
选用接收的Lamb波信号幅值为特征对铝板进行 B 扫描成像,扫描区域范围为0~100 mm,铝板B成像结果如图7所示。图7清晰反映出了缺陷在扫描方向上的位置和大小,且范围为40~60 mm 时,幅值显著减小,这一区域正是试样中通孔。
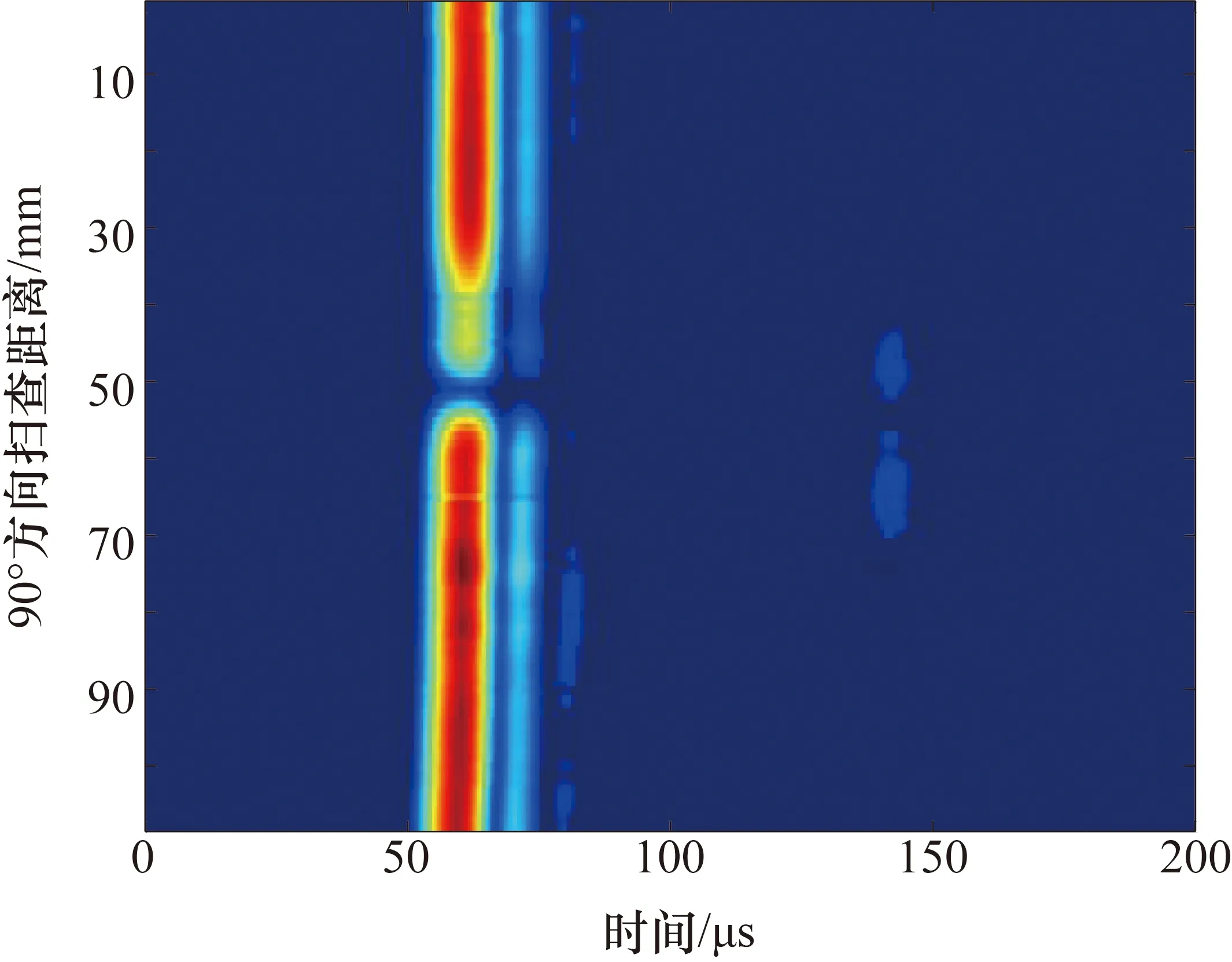
图7 铝板B扫描成像
采用空气耦合超声Lamb波对铝板的特征成像进行检测,选取无缺陷处的信号幅值能量作为基准,定义信号的能量差异系数(Signal Difference Coefficient,SDC)为特征值,作为扫查成像的依据。其计算公式为
(2)
式中:Fm为在铝板通孔损伤处的频域信号;Fn为铝板无损伤处的频域信号;f为频率;f1为截断频率的最小值;f2为截断频率的最大值。借助矩形窗截取损伤处及非损伤处Lamb信号,并对该信号进行快速傅里叶变换得到如图8所示的频谱图。通过对比直达Lamb波信号的频域能量,可对缺陷进行识别。
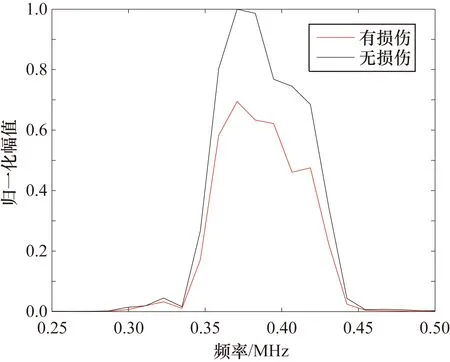
图8 A0模态Lamb波无缺陷与有缺陷信号的频谱图
对铝板Lamb波0°和 90°两个扫描方向上不同位置处的SDC值的变化规律进行比较分析,如图9所示。可以粗略确定铝板缺陷的位置,其中SDC值变化差异较大的部位通常是在铝板通孔缺口的中间部位,根据这一原理能更直观地对铝板缺陷进行Lamb波成像,缺陷可视化更明显。因此,可以将其作为判断铝板损伤情况的特征值。将铝板中没有缺陷的位置处的幅值能量作为基准值,SDC值的变化差异作为特征值,在不同扫查方向上通过全加和全乘进行数据融合,从而得到空耦Lamb波下的损伤重构图像,进而从重构图像中获取二维空间的信息。
s=s1(x,y)+s2(x,y)
s=s1(x,y)×s2(x,y)
(3)
式中:s(x,y)为相应的检测区域范围区间对应的像素点群。

图9 铝板Lamb波扫描信号SDC值
以SDC为特征值,通过全加与全乘的方式实现数据融合扫描成像结果如图10和图11所示。其扫描范围为106 mm×106 mm,幅值变化最明显的部位在图像中心区域,即铝板的通孔缺陷区域。比较全加和全乘两种融合方式,可以清楚看出,全乘法具有更高的缺陷分辨率和缺陷定位精度以及确定缺陷尺寸的准确性。
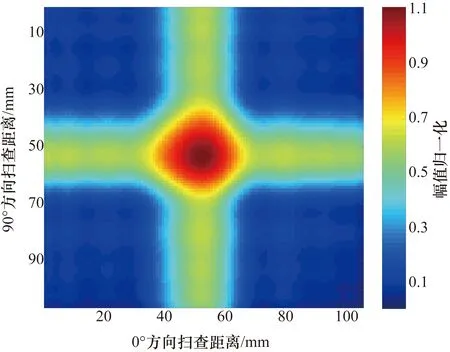
图10 特征值全加融合成像结果

图11 特征值全乘融合成像结果
3 结论
采用空气耦合Lamb波和基于损伤指数的成像方法,对铝板中的损伤开展了成像研究,得出以下结论。
① 通过空气耦合Lamb波检测方法可以激励出单一A0模态下的Lamb波,但必须满足Snell 定律。
② 在损伤范围内,Lamb波信号幅值呈衰减趋势,在通孔缺陷的中心处衰减到最小,以此为中心,两侧信号幅值变化呈对称分布。
③ 利用SDC这一特征值能够在数值上判断是否存在缺陷,可以用作铝板缺陷成像检测的参考依据。
④ 采取全加和全乘的方式将不同扫查方向上特征值进行数据融合能够较好地对铝板中的损伤进行重构和定位,通过对比全乘法和全加法的成像结果,表明全乘法的成像效果优于全加法。
