航空发动机气路检测静电传感器仿真研究
2022-12-07何双亮葛文庆孙忠湖毛玲阳
何双亮, 葛文庆, 孙忠湖, 毛玲阳
(四川泛华航空仪表电器有限公司,四川 成都 610500)
静电传感器的航空发动机气路检测技术是一种基于静电感应理论的新型航空发动机气路工作状态监测与故障诊断的技术[1-2],该技术使用静电传感器作为前端检测的敏感元件,获取发动机尾气静电水平的波动信息。由于发动机气路工况发生变化产生的颗粒物因摩擦、碰撞、高温等作用而带上的电荷属于微弱信号[3-4],所以静电传感器的性能会直接影响检测系统的准确性和敏感性,通过建模仿真的方式辅助静电传感器的设计是极其必要的。
目前,国际上对静电传感器的研究模型有Gajewski模型、Yan模型、Mumane模型等,但这些模型在建立的过程中需要大量假设条件,比较难以获取解析结果。在国内,李艳[5]、白杰[6]等进行了静电传感器的仿真,主要是根据传感器根据其电磁场的特性而进行的仿真分析。付宇等[7]建立了航空发动机尾气静电传感器空间物理模型,分析了空间感应数学模型。郭家琛等[8]介绍了航空发动机气路静电监测原理并建立了尾喷管棒状静电传感器的数值计算模型。
然而已发表的文献虽然对尾气静电传感器建立仿真模型,对不同尺寸的尾气静电传感器进行了数值分析,却并没有结合静电传感器的实际安装位置和发动机中的气路工况;航空发动机尾气静电传感器的工作环境属于典型的多物理场耦合环境,即计算域包括电场、流场、温度场和固体颗粒运动。流场存在高马赫数情况,需要考虑流体的可压缩性和激波效应,温度场为高温高压环境,需考虑介质热物理性质受温度和压力条件的影响。这些环境因素对仿真结果有着直接的影响。
结合发动机实际工况,采用有限元分析软件,设计一种多物理场深度耦合仿真方法,分析探针型静电传感器探极的直径、长度、布局位置对发动机尾气静电信号的影响规律,并通过尾气静电试验平台进行验证,为静电传感器的结构设计和工程化应用提供更为准确的理论支撑。
1 静电传感器模型
1.1 高马赫数湍流模型
1.1.1 控制方程
由于流场存在高马赫数情况,考虑到流体的可压缩性和激波效应,使用完全可压缩的Navier-Stokes方程并进行稳态计算。

(1)

(2)

(3)
式中:ρ为密度(kg/m3);u为速度矢量(m/s);p为压力(Pa);F为体积力矢量(N/m3);I为湍流强度的无量纲形式。
1.1.2 湍流模型
空气动力学中常用的湍流模型有k-ε、Spalart-Allmaras,与Spalart-Allmaras模型相比,探针模型中流体和热场温度耦合效应明显,k-ε模型更通用,更适合需要温度求解的模型,它可以给出合理的结果[9]。k-ε湍流模型中用湍动能k和湍动耗散率的ε关联湍动黏度计算公式为
(4)
式中:Cμ为经验常数,设为0.09。
对于k和ε为需要求解的物理量,在不可压流体中用下述两方程进行求解。
(5)
式中:几个模型常数默认为C1ε=1.44;C2ε=1.92;δk=1.0;δε=1.3。
由平均速度梯度引起的湍动能的增加计算公式为
(6)
1.1.3 传热模型
高马赫数流量接口适用于理想气体。通过选择气体常数类型并选择在恒定压力下输入热容或比热容之间来指定热力学性质[10]。其传热方程组为

(7)

(8)
式中:q为热通量(W/m2);Q为热源(W/m3);T为绝对温度(K)。
1.2 流体流动颗粒跟踪模型
对于流体流动中的颗粒运动,由动量微分方程得到:

(9)
式中:Ft为作用在粒子上的所有力的总和。
1.3 静电感应模型
静电计算采用稳态条件下的麦克斯韦方程组:

(10)

(11)
式中:E为电场强度(V/m);D为电通量密度(C/m2);ρv为电荷密度(C/m)。
2 仿真分析
2.1 静电探极的“流体-粒子-静电”耦合仿真
首先建立针型探极仿真模型,如图1所示,考虑到探针在发动机尾部仅有金属部分作用,将探针模型简化为直针,以提高计算效率;其次进行网格划分,在探针计算域中的固体区域将尽可能采用常规的结构化网格,在流体区域入口、出口、局部微小特征尺寸区域和其他急变流区域,引入辅助线对网格进一步局部加密,满足映射网格划分的精确性和整齐性要求[11],探极网络划分图如图2所示;最后定义物理场,采用有限元分析软件中的“湍流k-ε”模型描述计算域中的高速流动,打开“涡流”计算模型,使用Reynolds Average Navier-Stokes(雷诺时均NS方程),并对流场采用不可压缩流动进行简化,采用“Charged Particle Tracing”模型结合“Fluid-Particle Interaction”描述带电粒子在流场中的运动情况,在“指定时间释放”按照0.001 s时间间隔操作粒子释放,对于粒子和探极直接的交互作用,设定探极边界为接收区域,采用“Electrostatics”静电场模型结合“Particle Field Interaction,Non-Relativistic”多物理场接口描述带电粒子与静电探极之间的交互作用。
通过调整电极的位置和尺寸参数,探寻不同条件下对流场和电信号的影响规律,在流体流动颗粒跟踪中瞬态设置粒子随机生成,使用设定时间步长(0.001 s),在入口处随机产生10个带电粒子进行测算分析。

图1 针型探极仿真模型

图2 探极网格划分图
2.2 静电探极的“流-固-热”耦合仿真
首先建立探极几何模型,如图3所示,为详细了解针形探极在工作中的温度分布特点,按照原结构建立3D模型;其次进行网格划分,在所有的固体边界处采用超细化处理,对于探极部分,考虑到存在多复杂的细节结构,直接采用超细化的网格离散,并在局部位置加密,最终形成的探极网格划分如图4所示。
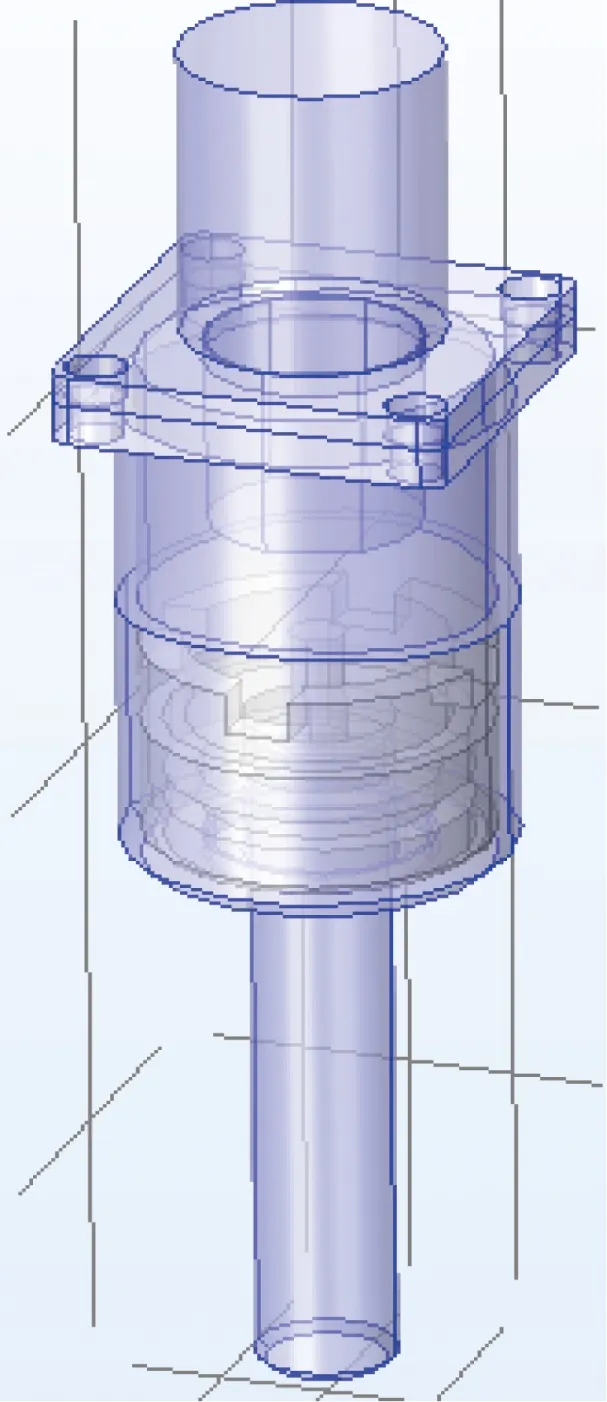
图3 探极几何模型图

图4 探极网格划分图
最后定义物理场,对于针形探极温度场,采用“流体传热”模块描述针形探极在气流道内的流热耦合作用。
设定入口温度为1000 K,初始压力值为绝对压力1 atm,采用域探针采集温度数据,基于COMSOL的仿真结果,分析针形探极在气流道中的结点温度。
3 针形探极的性能分析
3.1 探极直径对传感器性能的影响
设置参数d来表征探针形静电探极的直径,设置5组参数d=(2,4,6,8,10)mm,根据参数对结果的影响能够判断出静电探极直径大小对仿真结果的影响。
选取d=4和d=8两组数据作为对比,可以观察到d=8 mm时针形探极采集到的粒子电信号要明显比d=4 mm时少,如图5、图6所示。
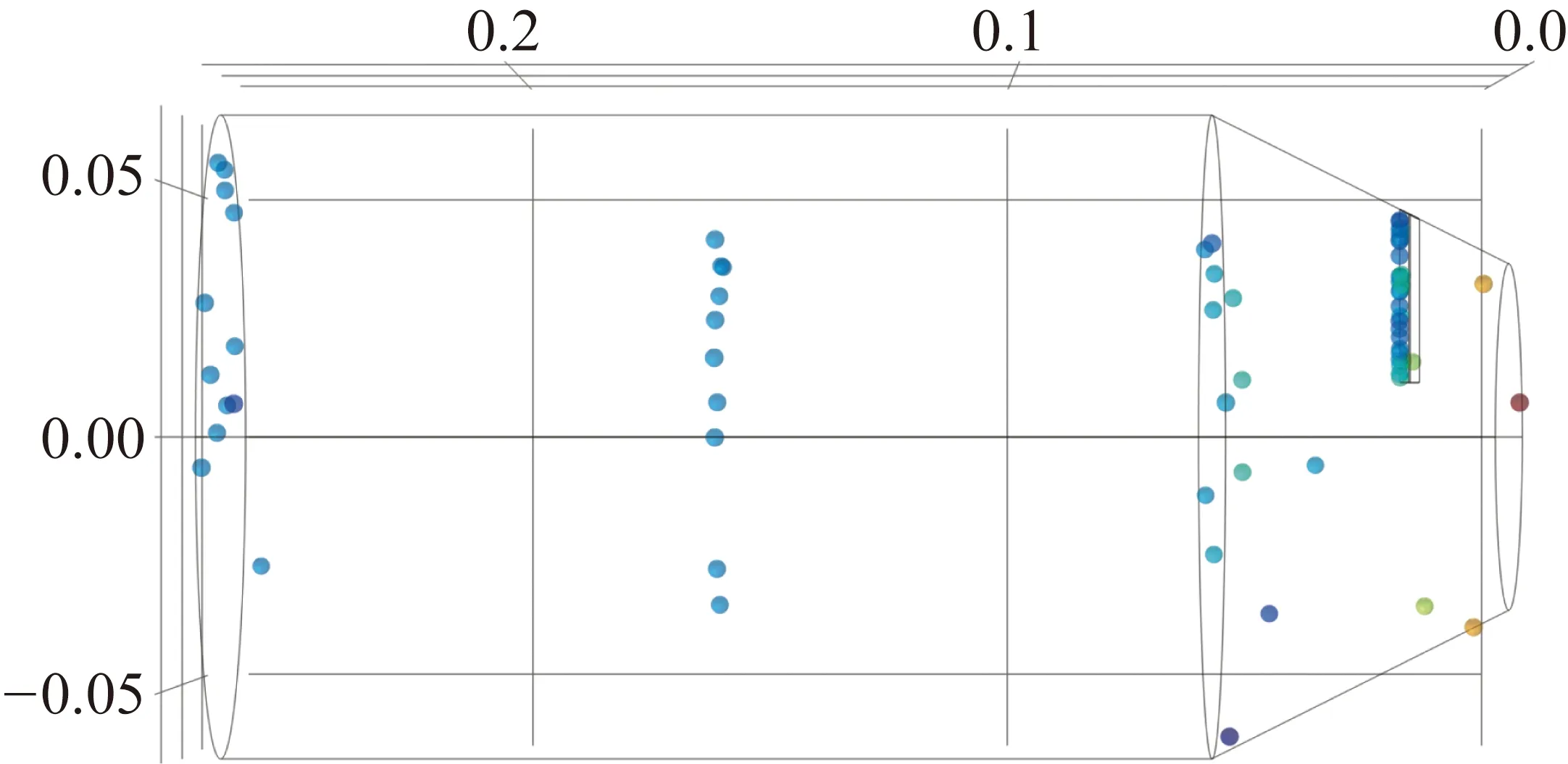
图5 d=4 mm时粒子轨迹图

图6 d=8 mm时粒子轨迹图
经过多次验算并对数据进行曲线拟合,如图7所示,得到探针直径在8 mm时采集到的电势平均值最小,在2 mm时采集到的电势平均值最大,但电势的波动较小。

图7 不同探针直径对电势平均值的影响
3.2 探极长度对传感器性能的影响
设置参数z来表征针形静电探极的长度,设置5组参数z=(10,15,20,25,30)mm,根据参数对结果的影响能够判断出静电探极长度大小对仿真结果的影响。
选取z=20和z=25两组数据进行对比,如图8、图9所示,图10为仿真结果拟合图。由图10可得出,长度增加针形探极采集到的电势平均值会增大,但是总体差距不大。z=20 mm时电势平均值较大,z=25 mm时电势平均值较小,但两者误差也在5%以内,两组数据的流场、电场均无明显差异。

图8 z=20 mm时粒子轨迹图
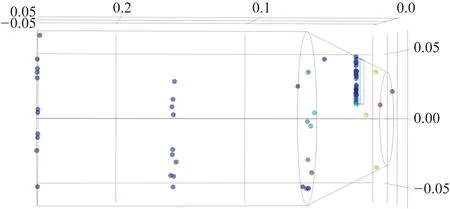
图9 z=25 mm时粒子轨迹图

图10 探极长度对仿真结果的影响
3.3 探极位置对传感器性能的影响
设置参数S来表征探极到尾流出口的距离,仿真中设置发动机尾部收缩段长度为60 mm,设置5组参数S=(10,20,30,40,50) mm,根据参数对结果的影响能够判断出静电探极位置对仿真结果的影响。选取S=10 mm、S=20 mm两组数据作为对比,如图11、图12所示,图13为仿真结果拟合图,可以观察到,S=10 mm时,探针处于急流区域,周围流体速度大,探针对流场阻力大,采集带电粒子电信号的概率更高,所以距离尾流出口越近电势的平均值就越高。

图11 S=10 mm粒子轨迹图

图12 S=20 mm粒子轨迹图
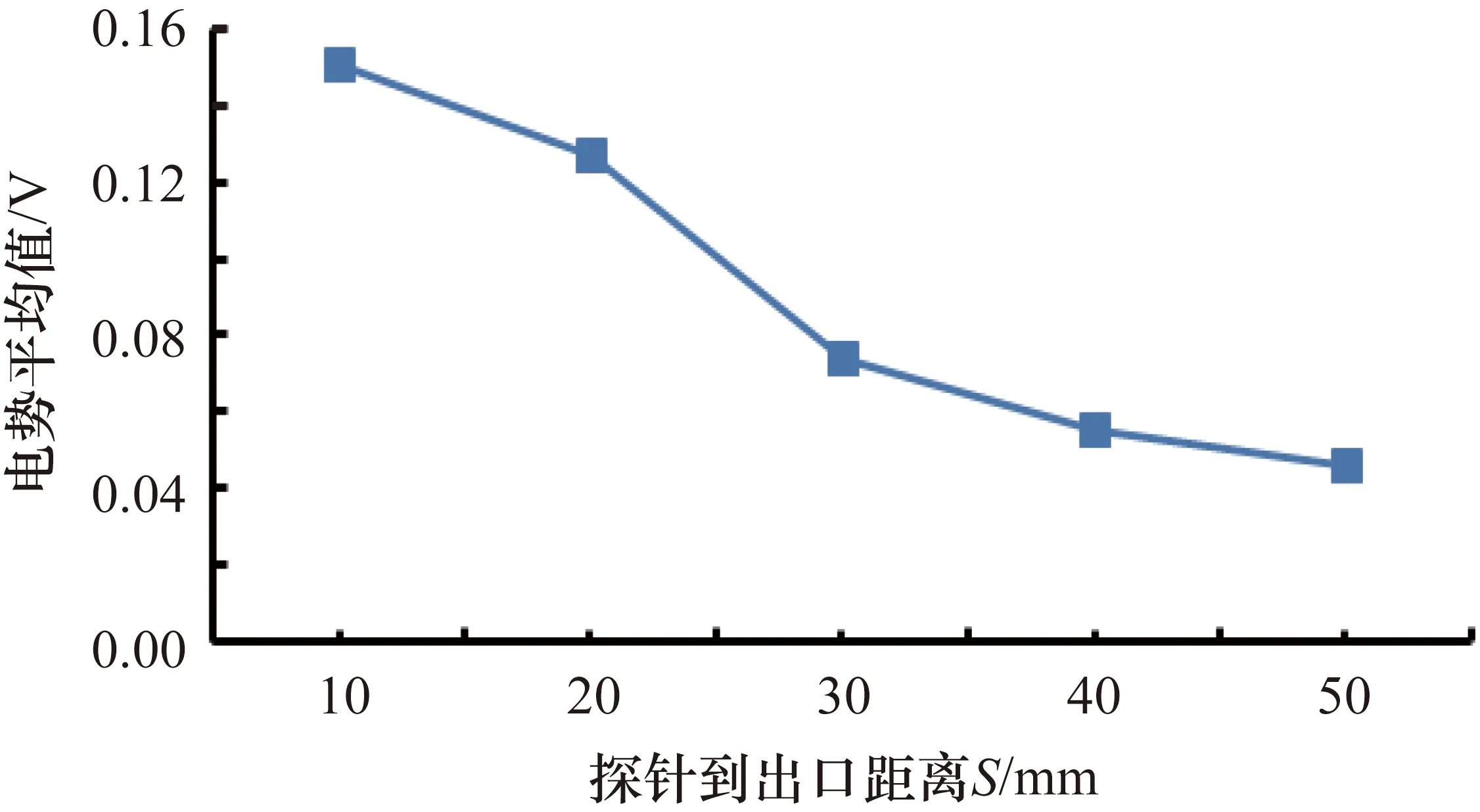
图13 探针到出口距离对电势平均值的影响
4 测试验证
按仿真结果将设计的系列尾气静电传感器安装在尾气静电试验平台上,使其与静电信号放大处理装置相连,再通过示波器对其信号进行监测,开动涡喷发动机,保持在转速50000 r/min、尾气温度为560 ℃的条件下,每次在尾气中加入50目的不锈钢金属颗粒0.01 g,测试的结果分别见图14~图19,可以看出符合多物理场深度耦合仿真分析的结论。

图14 直径2 m探极信号
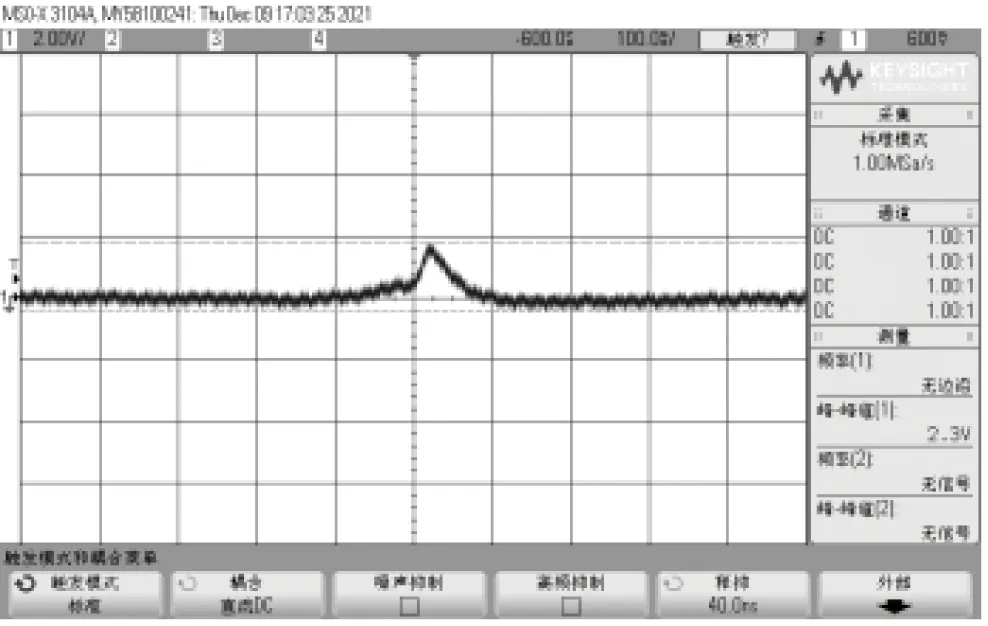
图15 直径10 mm探极信号

图16 探极长10 mm信号

图17 探极长30 mm信号

图18 探极距端口50 mm信号
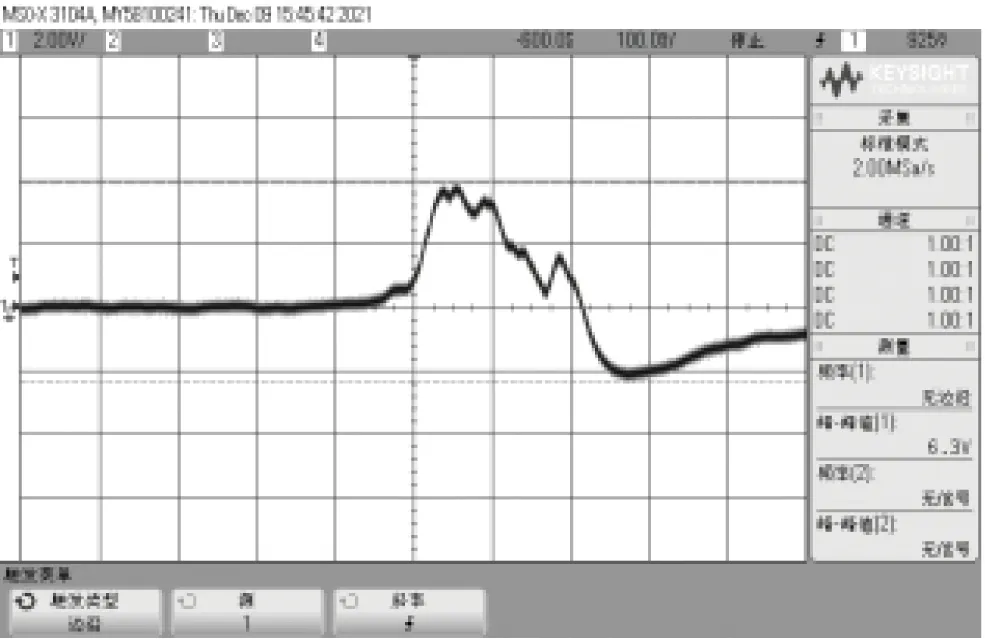
图19 探极距端口10 mm信号
5 结论
根据针形探极的流场、温度场、电场仿真结果分析,对于针形静电探极可以得出初步结论如下。
① 针形探极直径对电信号采集的影响并不明显,结合流场来看,选取直径为2 mm的针形探极即可。
② 针形探极长度对电信号采集总体呈正相关,排除数据扰动,总体上呈现探极越深入,灵敏度越好,采集到的电势平均值越高。考虑到探极深入对流场扰动变大,流阻增加,建议金属针长度为20 mm。
③ 针形探极位置对电信号采集有明显影响,由于发动机尾部有收缩段,流体速度在此激增,探极越靠近尾部出口,采集到的电势平均值越高,即灵敏度越高。
④ 对于针形探极温度场,按照入口温度1000 K设定,仿真结果显示径向深入气流道内40 mm处的探极头部温度高达998.24 K,紧贴气流道壁面的基座部分节点温度范围在930~967 K之间,远离气流道的探极尾部温度也有870.86 K,设计传感器时需考虑材料的耐温性能。
