基于ISSA-LSTM 的浓缩池溢流浓度预测

2022-12-07张洋洋樊玉萍马晓敏董宪姝金伟王大卫

工矿自动化 2022年11期

张洋洋，樊玉萍，马晓敏，2，董宪姝，金伟，王大卫

（1. 太原理工大学矿业工程学院，山西太原 030024；2. 矿物加工科学与技术国家重点实验室，北京 100160；3. 晋能控股集团马道头选煤厂，山西太原 030006）

0 引言

煤炭洗选过程会产生大量煤泥水，若直接排放会造成矿山环境污染及水资源浪费[1]。通过添加絮凝剂对煤泥水进行浓缩是实现细粒级煤泥和水固液分离的有效途径之一。絮凝剂的添加量（即加药量）是影响浓缩效果的一个关键因素，而溢流浓度可直接反映絮凝沉降效果。目前，我国一部分选煤厂已实现加药自动化，通过传感器监测溢流浓度，再根据溢流浓度调节加药量。但是煤泥水浓缩是个大滞后的过程，基于传感器的溢流浓度监测方式会导致絮凝剂调节滞后，从而可能造成溢流浓度升高，浓缩效果变差。近些年，为了落实“中国制造2025”的强国战略，智能化建设热潮开始在选煤行业兴起[2-3]。在选煤厂智能化建设背景下，为合理添加絮凝剂，保证浓缩效果，需要构建精确、高效的溢流浓度预测模型，实现溢流浓度实时监测，从而指导絮凝剂调节。

随着深度学习技术的突破，众多深度学习模型被应用到矿业领域的预测中，主要包括浮选过程药剂量与灰分预测[4]、工作面矿压预测[5]、煤矿突水预测[6]等。在众多深度学习模型中，长短期记忆（Long Short Term Memory，LSTM）网络能够有效利用长距离的时序信息，并考虑非线性因素与时序数据之间的关系。溢流浓度数据具有时序性，且受外部因素的干扰，因此，LSTM 网络适用于溢流浓度预测。

在深度学习模型建立和训练过程中，超参数设置很关键，若设置不恰当会导致模型欠拟合或过拟合，难以达到预期效果。解决这一问题的办法主要是采用优化算法进行超参数寻优，优化算法主要包括改进鲸鱼优化算法（Whale Optimization Algorithm，WOA）[7]、粒子群优化（Particle Swarm Optimization，PSO）算法[8]、量子粒子群算法[9]、改进PSO 算法[10]等。麻雀搜索算法（Sparrow Search Algorithm，SSA）是新型群智能优化算法，在处理多维寻优问题时表现出较强的性能，已被成功应用于无人机航迹规划[11]和电池堆参数优化识别[12]等，但是SSA 存在迭代过程中种群多样性降低、易陷入局部最优等不足。

针对上述问题，本文采用多策略对SSA 进行联合改进，用改进 SSA（Improved SSA， ISSA）对LSTM 网络模型的超参数进行寻优，再通过优化LSTM 网络模型进行浓缩池溢流浓度预测。

1 煤泥水浓缩工艺流程

煤泥水浓缩工艺流程如图1 所示。在制药装置中配置出一定浓度的絮凝剂溶解液，根据入料浓度和流量控制螺杆泵将絮凝剂添加到浓缩池的入料管道中，与待处理的煤泥水混合后进入浓缩池中进行浓缩沉降。通过溢流浓度计监测溢流浓度，判断需要调节的加药量，再通过控制柜调整变频器输出频率，从而达到调节加药量的目的。

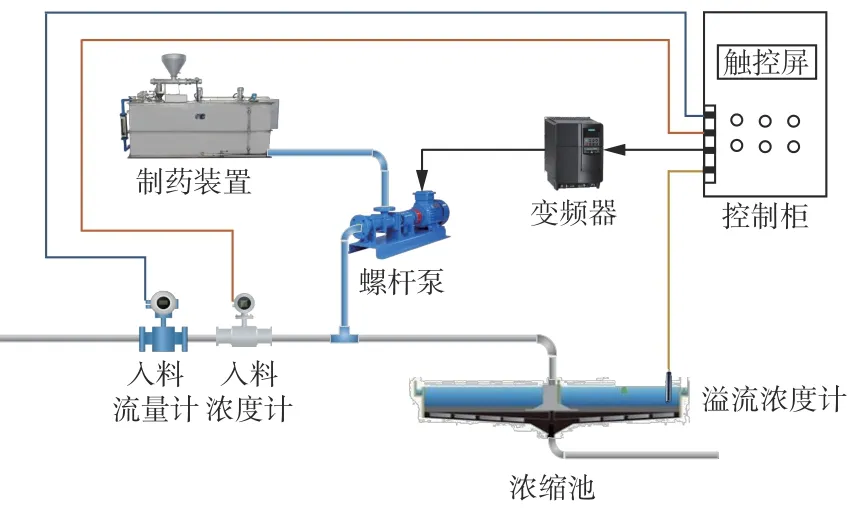
图 1 煤泥水浓缩工艺流程Fig. 1 Concentration process flow of coal slurry

2 浓缩池溢流浓度预测方法

2.1 数据预处理

实验采用山西某选煤厂煤泥水浓缩池的工作运行数据，共计100 组，包括5 个变量：入料流量Z1，入料浓度Z2，加药量Z3，底流浓度Z4，溢流浓度Z5。

2.1.1 相关性分析

强相关数据在建模过程中对模型的贡献相近，引入这种数据会增加计算量，甚至影响模型预测精度。因此，对各变量之间的相关性进行分析，以剔除强相关数据。选用Spearman 相关系数 ρ对实验数据进行分析，结果如图2 所示。可看出5 组数据之间不存在强相关关系（ |ρ|=0.6～1.0），因此不需要剔除。

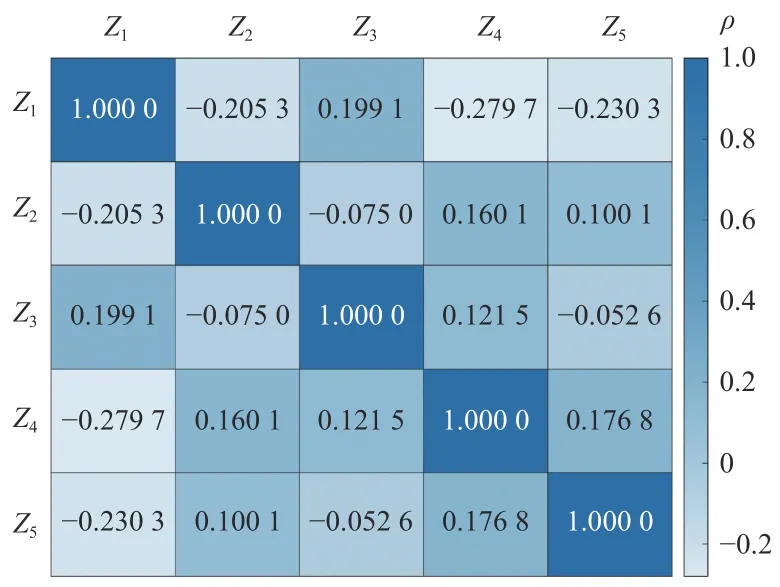
图 2 Spearman 相关性分析热力图Fig. 2 Thermodynamic diagram of Spearman correlation analysis

2.1.2 数据降噪

在实验过程中，由于数据采集现场环境恶劣，干扰因素较多，采集到的数据会出现异常跳动，即存在噪声数据。噪声数据会降低模型的预测精度，因此需进行降噪处理。根据监测数据的变化特点和扰动信号的性质，选用Savitzky-Golay 平滑去噪算法（简称S-G 算法）对入料流量、入料浓度、加药量进行降噪处理。S-G 算法参数见表1。降噪前后入料流量对比如图3 所示。

表 1 S-G 算法参数Table 1 Parameters of S-G algorithm

图 3 降噪前后入料流量对比Fig. 3 Comparison of feed flow before and after noise reduction

采用移动均值算法对底流浓度和溢流浓度进行降噪处理，平滑因子分别为0.10 和0.15。降噪前后溢流浓度对比如图4 所示。

图 4 降噪前后溢流浓度对比Fig. 4 Comparison of overflow concentration before and after noise reduction

2.1.3 归一化处理

采用min-max 标准化方法将5 组实验数据映射到[0，1]进行归一化处理，以消除指标之间量纲差异的影响。设zab为第b（b=1,2,···,5）个指标的第a个值，则归一化处理后的值为

2.2 双层LSTM 网络模型

LSTM 网络模型是循环神经网络（Recurrent Neural Network，RNN）的一种改进模型，通过引入门控单元结构来控制信息的传递量，因此可以决定历史信息和实时信息的记忆和遗忘程度，并增加了记忆存储单元，能够有效记忆数据间的特征，具有长期记忆功能，避免了RNN 可能出现的梯度爆炸和梯度消失问题。

通过增加LSTM 网络模型的深度，能够深度挖掘数据特征，提高网络预测精度[13-14]。但是过度增加模型深度会导致过拟合，且训练时间长；若模型深度过小，则不能提取复杂数据特征，从而学习不到输入变量与输出变量之间的映射关系，产生欠拟合问题。因此，本文通过前期实验，构建出双层LSTM 网络模型，如图5 所示。该模型由上到下包括1 个输入层、2 个LSTM 层、1 个全连接层和1 个回归层。数据首先由输入层进入网络，然后逐层传递实现输入特征提取，最后经过全连接层得到预测值，通过回归层输出预测值。

图 5 双层LSTM 网络结构Fig. 5 Structure of double-layer LSTM network

2.3 SSA 及其改进

2.3.1 SSA

SSA 的主要思想来源于麻雀的觅食和反捕食行为[15]。在自然界中，麻雀种群在觅食过程中分为2 个部分，一部分麻雀负责提供种群的觅食区或方向，剩余麻雀跟随前者获取食物；当麻雀发现捕食者时发出警报，种群则放弃食物并更换种群位置[16]。基于此，SSA 根据理想化的行为规则建立数学模型，将麻雀种群中的个体分为发现者和跟随者，并随机分布一定数量的警戒者[17]，每个个体的位置代表1 个解。在觅食过程中，通过不断更新三者位置完成资源获取。

在SSA 中，发现者通常具有较大的适应度值，会优先获取食物，并负责搜索食物，为所有跟随者提供觅食方向。因此，发现者的觅食搜索范围比跟随者大。在迭代过程中，发现者位置更新公式为

跟随者由于适应度值较小，所以时刻监视发现者，当发现者发现更好的食物时，跟随者便改变当前位置，与发现者进行争夺。若跟随者争夺成功，则立即获得该发现者的食物，否则进行位置更新，更新公式为

在SSA 中，通常假设意识到危险的麻雀占总数的 10%～20%，并且其初始位置在种群中随机产生。该类麻雀的位置更新公式为

式中：为当前全局最优位置；β为步长控制系数，为服从标准正态分布的随机数；fi，fg，fw分别为当前个体适应度值、全局最优适应度值和最差适应度值；K为[-1，1]的随机数；ε为常数，用于避免出现分母为0 的情况。

2.3.2 多策略联合改进

从SSA 的迭代寻优过程可知，SSA 的寻优能力受种群中个体质量的影响，一旦陷入局部最优，将难以跳出当前局部空间。另外，跟随者位置主要根据或者进行更新，没有充分利用种群中其他大多数个体所携带的信息，降低了算法在全局范围内的搜索能力。当SSA 处理复杂的高维问题时，一旦发现者陷入局部最优，整体将难以跳出当前的局部空间。

为增强SSA 的全局搜索能力，避免陷入局部最优，加快收敛速度，采用以下策略进行联合改进：采用Tent 映射对麻雀种群进行初始化，使个体尽可能均匀分布在搜索空间内，增强初始种群的多样性；将螺旋捕食策略应用到跟随者位置更新过程中，以兼顾局部开发和全局搜索能力；用萤火虫扰动策略对所有麻雀的位置进行扰动，增强算法跳出局部最优的能力，扩大搜索范围，提升全局搜索能力。

（1） Tent 映射。传统的随机初始化方式难以保证种群的多样性，而混沌映射产生的序列具有随机性和遍历性等特点，能够使算法容易跳出局部最优，从而可以维持种群的多样性，同时提高全局搜索能力[18]。混沌映射包括Logistic 映射、Tent 映射、余弦映射及Circle 映射等，其中Tent 映射性能较好，能够产生较均匀的混沌序列[19]。Tent 映射产生的混沌值与随机值对比如图6 所示。

图 6 Tent 映射混沌值与随机值对比Fig. 6 Comparison of chaotic value and random value of Tent map

从直方图可看出，混沌值序列分布较均匀，而随机产生的值则集中分布在[0，0.33]和[0.5，0.83]这2 个区间。

混沌值计算公式为

式中：wi,d为第d个混沌值，d=1，2，…，j；h为混沌参数，h∈(0，1]。

根据式（5）得到混沌值，将混沌值转换至种群的搜索空间中，即可生成种群个体的初始位置变量Xi,j=[xi,1xi,2···xi,j]，xid为第i个个体中第d维的初始位置。

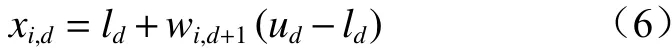
式中ud和ld分别为第d维搜索范围的上界和下界。

（2）螺旋捕食策略。在标准SSA 中，跟随者的位置往往容易被发现者的最优位置影响，发现最优位置后，种群会在短时间内向该位置迅速收缩，虽然能提升算法收敛速度，但种群多样性也会在短时间内降低，致使算法的全局搜索能力变弱，大大增加陷入局部最优的概率。针对该问题，将WOA 中的螺旋捕食策略引入跟随者的位置更新过程中。螺旋捕食策略是指在鲸鱼与猎物之间创建一个螺旋等式，模仿座头鲸的螺旋状移动[20-21]。该策略既保证了收敛性，又兼顾了种群多样性，能够很好地平衡局部开发和全局搜索能力。改进后跟随者位置更新公式为

式中：D′为第t次迭代时麻雀与食物（当前最优解）之间的距离，D′=；c为定义螺旋线形状的常数；v为[-1，1]的随机值。

（3）萤火虫扰动策略。在SSA 迭代后期，由于麻雀个体的同化，导致算法易陷入局部最优。针对该问题，采用萤火虫扰动策略对所有麻雀位置进行一次扰动更新，增强其跳出局部最优的能力。萤火虫扰动策略是指根据萤火虫亮度进行移动，从而得到新的位置[22]。扰动后麻雀位置更新公式为

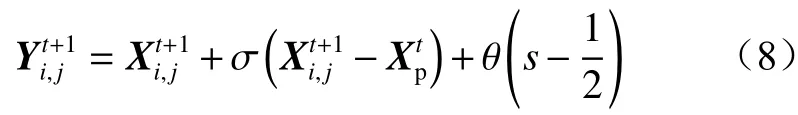
式中：σ为吸引度，σ=σ0exp()， σ0为最大吸引度， γ为光强吸收系数，ri,j为与之间的距离；θ为步长因子，取值范围为[0，1]；s为[0，1]上均匀分布的随机数。

改进后得到的ISSA 流程如图7 所示。

图 7 ISSA 流程Fig. 7 Flow of improved sparrow search algorithm

2.4 溢流浓度预测模型构建

基于ISSA-LSTM 的浓缩池溢流浓度预测模型如图8 所示。

图 8 基于ISSA-LSTM 的浓缩池溢流浓度预测模型Fig. 8 Prediction model of overflow concentration of thickener based on ISSA-LSTM

（1）对煤泥水浓缩过程监测到的数据集进行预处理，并按照8∶2 的比例划分为训练集和测试集。

（2）构建双层LSTM 网络模型，选择Adam 作为学习过程的优化算法[23]，采用L2 正则化防止模型过拟合。

（3）设置优化算法的最大迭代次数tmax、空间维度j、种群规模N及LSTM 网络模型的5 个超参数，包括2 个LSTM 层的单元数、迭代次数、初始学习率和L2 正则化因子。

（4）初始化种群，将麻雀位置映射为超参数的值，以均方根误差作为个体的适应度值。

（5）采用ISSA 算法寻找最优值，并记录寻找到的位置和适应度值。

（6）判断优化算法是否达到最大迭代次数tmax，若达到则输出最优超参数，将其赋予LSTM 网络，否则返回步骤（5）。

（7）采用输出的超参数构建溢流浓度预测模型，根据输入得到溢流浓度预测值。

3 实验研究

3.1 预测效果评价标准

选用均方根误差（Root Mean Square Error，RMSE）和平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）作为ISSA-LSTM 溢流浓度预测模型效果的评价标准。RMSE 能够描述预测值与实际值的非线性拟合度，值越小，说明预测值越接近实际值；MAPE 表示预测值与实际值的平均偏离程度，值越小，说明预测模型精度越高。设RMSE，MAPE 的值分别为 δRMSE，δMAPE，其计算公式为

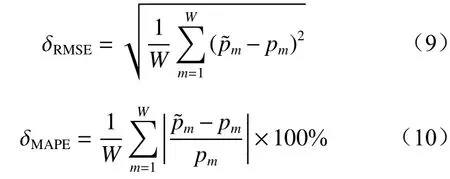
式中：W为测试集数据个数；m为采用ISSA-LSTM模型得到的溢流浓度预测值；pm为溢流浓度实测值。

3.2 降噪效果验证

为验证数据降噪对溢流浓度预测精度的影响，将降噪前后各100 组实验数据分别按照8∶2 的比例划分训练集与测试集，用ISSA-LSTM 预测模型进行对比实验，结果见表2。

表 2 降噪前后预测结果Table 2 Prediction results before and after noise reduction

从表2 可看出，降噪后实验数据的预测精度更高，RMSE 约是降噪前的1/9，MAPE 与降噪前相比下降了30.25%。这是由于原始实验数据中存在噪声，直接输入预测模型会导致拟合效果较差，而数据降噪可以降低噪声所占比例，从而使预测精度大幅提升。

3.3 ISSA 性能测试

为了验证ISSA 的寻优效果，选取Ackley 函数和Rastrigin 函数作为测试函数，并与PSO 算法、WOA 及标准SSA 进行对比。

Ackley 函数是一种多峰优化算法测试基准函数，存在众多局部最优解和1 个全局最优解，如图9所示。可看出Ackley 函数的最优解位于中心的孔洞中，周围分布着许多局部极值，孔洞的外部则较为平坦。因此，寻优过程中越靠近中心，越容易陷入局部最优，从而使优化算法难以寻找到全局最优解。Ackley 函数表达式为

通信电子电路是一门既需要理论研究基础，工程性又非常强的课程，在电子通信类专业课中起着承上启下的重要作用。课程主要学习关于无线通信系统中用于信息传输和信息处理方面各个基本功能的电路模块。通过对本课程的学习，学生需要掌握通信系统的工作原理，通信电子电路中各基本功能模块的组成、性能指标和基本的分析方法，以及常用的通信电路系统分析、设计和应用能力。

图 9 Ackley 函数Fig. 9 Ackley function

式中：xk(k=1，2，···，n)为自变量，取值范围为[-32，32]，定义域内最小值为0；n为函数的维数。

Rastrigin 函数同样也是一种具有多个局部极小值的多峰函数，如图10 所示。其搜索空间大，且在最优解周围分布着众多不同的局部极值，因此求取全局最优解也相当困难。Rastrigin 函数表达式为

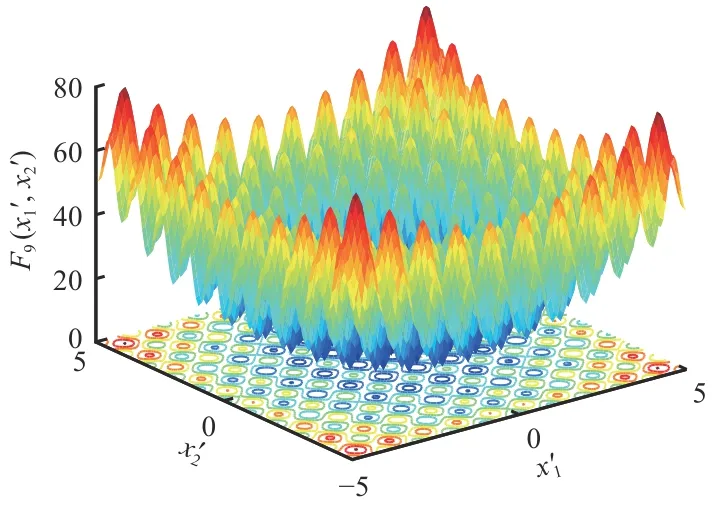
图 10 Rastrigin 函数Fig. 10 Rastrigin function

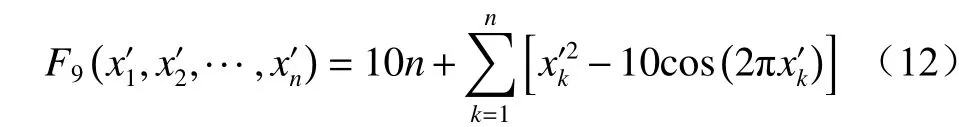
测试时，为了去除偶然因素引起的误差，分别对4 种优化算法进行20 次独立实验，最后结果取平均值。设置最大迭代次数tmax=1 000，维数j=5，测试结果如图11、图12 所示。

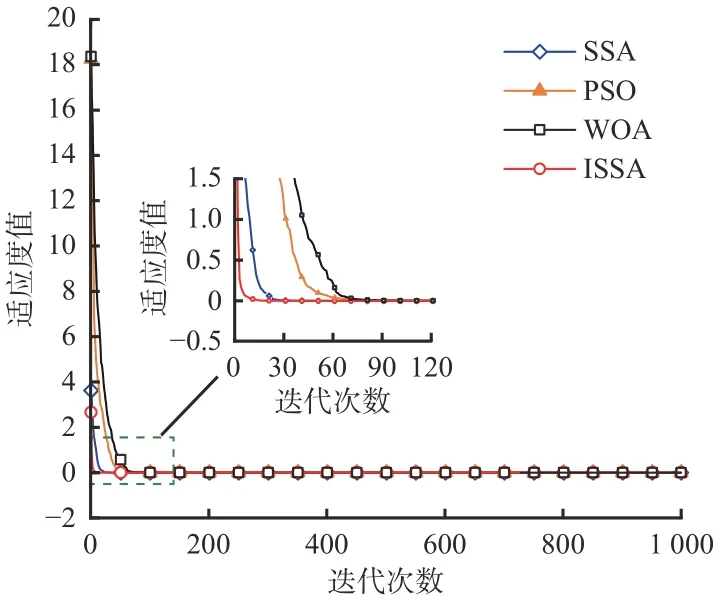
图 11 不同优化算法的Ackley 函数收敛曲线Fig. 11 Convergence curves of Ackley function of different optimization algorithms

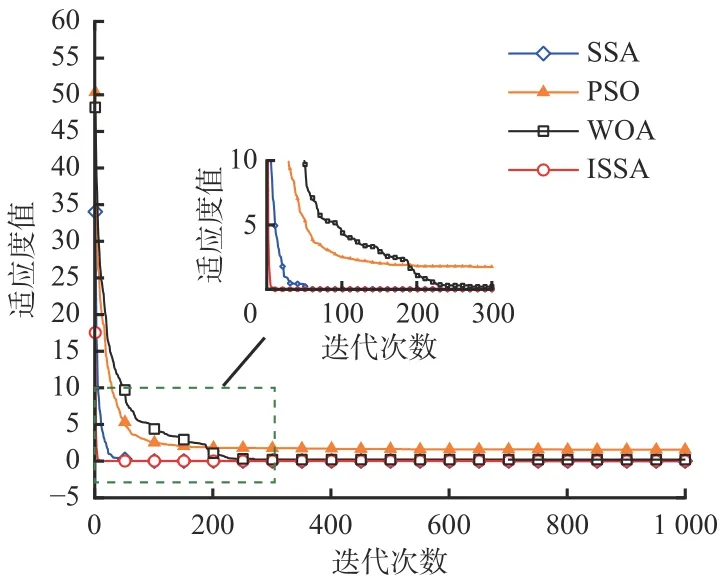
图 12 不同优化算法的Rastrigin 函数收敛曲线Fig. 12 Convergence curves of Rastrigin function of different optimization algorithms

由图11 和图12 可以看出，采用Ackley 函数测试时，4 种优化算都能够快速收敛，都搜寻到了最小值，其中ISSA 最先达到平稳状态，收敛速度最快。采用Rastrigin 函数测试时，PSO 和WOA 都陷入了局部最优且未能跳出；SSA 在迭代次数为30～50 时陷入1 次局部最优并成功跳出，搜寻到全局最优解，说明SSA 的性能优于PSO 和WOA；ISSA 未陷入局部最优，表现出了优秀的全局搜索能力及快速的收敛性，说明ISSA 的全局寻优性能和收敛速度均优于PSO、WOA 和标准SSA。

3.4 不同改进策略对比分析

为进一步探索ISSA 性能影响因素，采用混沌映射、螺旋捕食、萤火虫扰动中的2 种进行寻优对比实验，设置3 种改进策略，对应算法分别命名为ISSA1，ISSA2，ISSA3，见表3。实验结果如图13、图14 所示。

表 3 SSA 改进策略Table 3 Improvement strategies of sparrow search algorithm

图 13 不同改进策略的Ackley 函数收敛曲线Fig. 13 Convergence curves of Ackley function of different improvement strategies

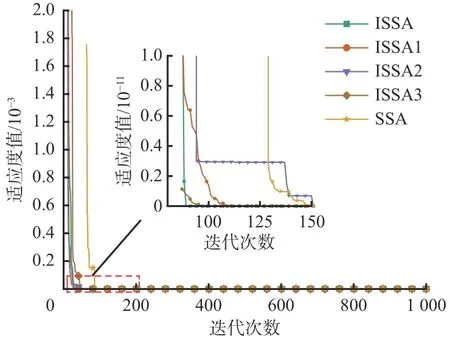
图 14 不同改进策略的Rastrigin 函数收敛曲线Fig. 14 Convergence curves of Rastrigin function of different improvement strategies

由图13 和图14 可知，5 种算法都搜索到了最小值，其中ISSA 收敛速度最快且未陷入过局部最优，而其他3 种改进策略的收敛速度都有不同程度下降，从快到慢依次是ISSA3，ISSA1，ISSA2。在2 个测试函数的寻优过程中，ISSA2 均明显陷入局部最优，导致收敛速度变慢，说明在SSA 后期寻优过程中，物种多样性的降低会使优化算法易陷入局部最优。在Ackley 测试函数的收敛曲线上，与ISSA 相比，可以明显看到ISSA3 陷入过1 次局部最优，说明去除萤火虫扰动后，算法的全局搜索能力有所减弱。基于此，可得出螺旋捕食策略对ISSA 性能的提升起主导作用，混沌映射和萤火虫扰动策略协调算法的收敛速度和全局搜索能力，进一步提升算法寻优性能。

3.5 ISSA-LSTM 网络模型的训练及优化结果

3.5.1 实验条件及超参数设定

表 4 设备硬件参数Table 4 Equipment hardware parameters

设置ISSA 种群规模为30，最大迭代次数为100，LSTM 网络的超参数设置见表5。

表 5 超参数设置Table 5 Setting of hyperparameters

3.5.2 优化结果

采用标准SSA 和ISSA 对LSTM 网络的超参数进行寻优，结果如图15 所示。

由图15 可知，ISSA-LSTM 的适应度值比SSALSTM 小，说明ISSA 比SSA 具有更强的跳出局部最优的能力，即全局寻优性能更好，并且ISSA 收敛速度更快。SSA 寻找到的最优超参数：M1=65，M2=10，I1=0.074，I2=0.003。ISSA 寻找到的最优超参数：M1=125，M2=10，I1=0.068，I2=0.064。

3.6 不同模型对比分析

为验证ISSA-LSTM 模型的预测精度，与双层LSTM 模型、SSA-LSTM 模型及最小二乘支持向量机（Least Squares Support Vector Machines，LSSVM）模型进行对比。双层LSTM 模型中，设置最大迭代次数为400，初始学习率为0.02，学习率衰减因子为0.008；SSA-LSTM 模型中，设置最大迭代次数为400，种群数量为30，优化算法的最大迭代次数为100；LSSVM 模型中，正则化参数和径向基函数（Radial Basis Function，RBF）的参数分别设置为0.5 和0.4。不同模型预测结果对比如图16 所示，评价指标对比见表6。

图 15 适应度曲线对比Fig. 15 Comparison of fitness curves

图 16 不同模型预测结果对比Fig. 16 Comparison of prediction results of different models

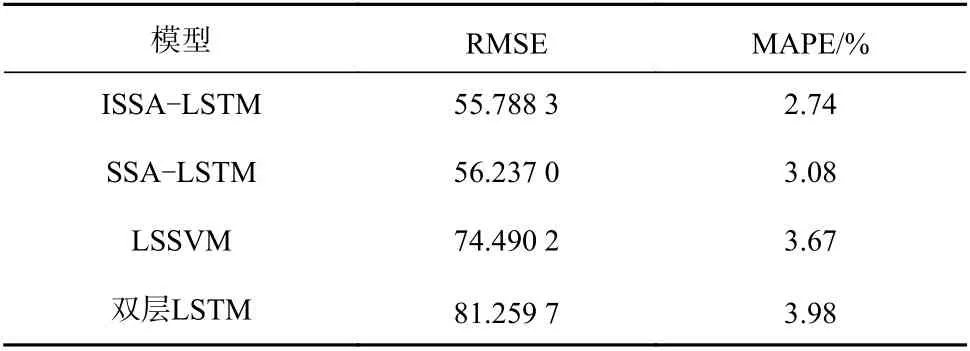
表 6 不同模型评价指标对比Table 6 Comparison of evaluation indicator of different models

由图16 和表6 可知，双层LSTM 模型的预测误差最大，RMSE 和MAPE 比ISSA-LSTM 模型高25.471 4 和1.24%，说明超参数对模型的影响较大；LSSVM 模型用于长时间序列预测时表现稍差，RMSE 和MAPE 比ISSA-LSTM 模型高18.701 9 和0.93%；SSA-LSTM 模型因为采用SSA 进行超参数寻优，RMSE 和MAPE 分别比双层LSTM 模型降低了25.022 7 和0.9%，但比ISSA-LSTM 模型高0.448 7和0.34%。ISSA-LSTM 模型的RMSE 和MAPE 的值分别为55.788 3 和2.74%，均低于其他对比模型，溢流浓度预测精度达97.26%，验证了将ISSA-LSTM 模型用于溢流浓度预测的有效性。