基于优化模型的反射面板调节问题研究
2022-12-07周莉
周 莉
(西安建筑科技大学(草堂校区),陕西 西安 710399)
1 观测天体位于基准球面正上方模型的建立与求解
1.1 模型的建立
根据FAST剖面示意图,基准球面半径为300m,焦径比为0.466,工作抛物面的口径为300m,可得观测卫星位于基准球面正上方时的几何示意图。
根据几何示意图,焦面球心的半径为:

式中,R为基准球面半径,F为同心球面的半径差。
以基准球面的最低点为坐标原点,由焦面球心的半径求得焦点P的坐标,可以得到一条理想的抛物线方程为:

将抛物线绕Z轴旋转可进一步得到理想的抛物面方程为:
1.2 模型的求解
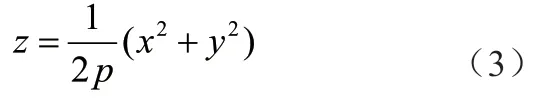
Step1:求解以基准球面最低点为坐标原点的理想抛物面
由式(1)可求得焦面球心的半径r=250.2m,焦点P的坐标为(0,0,139.8),即 2p=559.2,将其代入式(3)中可得理想抛物面方程为
Step2:求解以基准球面的球心为坐标原点的理想抛物面
将以基准球面的最低点为坐标原点的坐标轴向上平移300m,可得理想抛物面方程为:
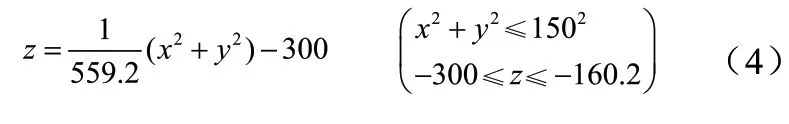
2 观测天体偏离基准球面正上方模型的建立与求解
2.1 模型的建立
当观测天体偏离基准球面时,确定对应的理想抛物面。需要考虑欧拉角得到旋转矩阵,再通过旋转变换确定理想抛物面方程。通过调节促动器的伸缩量使反射面尽量贴近理想抛物面,以照明区域内反射面板数量最多为目标函数,建立优化模型,使得反射信号接收效果最佳。
2.1.1 理想抛物面方程

代入得到Q点坐标(-49.254,-36.840-293.627):
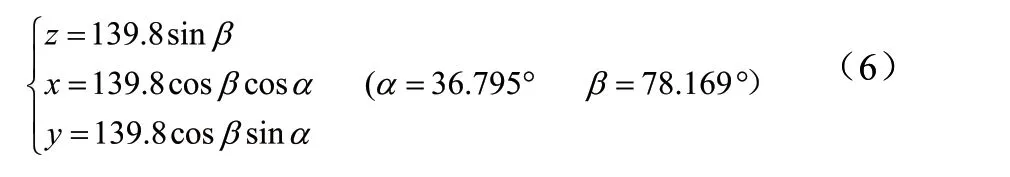
代入得到P点坐标。
当观测天体偏离基准球面时,根据天体S方位角与仰角示意图,=78.169°,=36.795°对于三维空间坐标轴的变化可以用3个欧拉角表示。在天体旋转的过程中,坐标轴会随着天体的转动做相同的转动。
绕X轴旋转的欧拉角ψ为36.5°,再绕Y轴旋转的欧拉角ϕ为350.95°,之后绕Z轴旋转的欧拉角θ为7.1°,则对应欧拉角的旋转矩阵分别为:
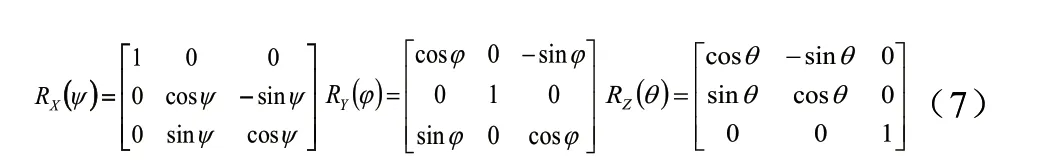
那么,利用所求欧拉角ψ、ϕ、θ及式(6)可推导出最终的旋转矩阵为:

利用旋转变换公式可以得到绕坐标轴旋转变换后的坐标(x' ,y',z')T及理想抛物面的方程式为:

联立式(11)和式(12),可得在空间直角坐标系中,观测天体偏离基准球面情况下的理想抛物面方程为:
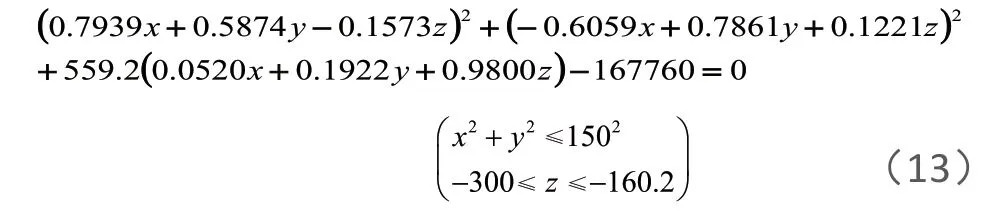
2.1.2 基于优化模型的反射面板调节
(1)目标函数
设基准球面上促动器顶端的坐标(x0,y0,z0),理想抛物面上促动器顶端的坐标(x1,y1,z1)。则基准球面上的主索节点到球心的距离R0和理想抛物面上的主索节点到球心的距离R1为:

优化的目标是使反射面尽量贴近理想抛物面,使在照明区域内的反射信号达到最佳接收效果,以此来建立优化目标函数:
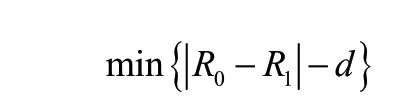
式中,d为促动器的伸缩量。
(2)约束条件
促动器的顶端沿基准球面径向伸缩来完成下拉索的调节,从而调节反射面板的位置形成抛物面。由促动器的工作原理可知,促动器的径向伸缩量d就等于对应的促动器顶端从基准球面移到理想抛物面上的距离。利用欧式距离公式,可求得促动器的径向伸缩量为:
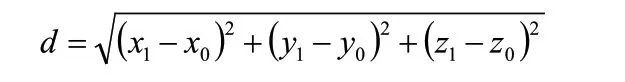
由于促动器的伸缩范围为-0.6~+0.6m,反射面均在空间直角坐标系XOY平面下方。为满足优化模型中目标函数的求解,故综合以上条件,可以得出约束条件为:

2.2 模型的求解
Step1:几何变换求解理想抛物面。当观测天体偏离基准球面时,通过绕坐标轴旋转得到欧拉角,进而得到旋转矩阵,然后通过旋转变换公式确定理想抛物面。
Step2:确定基准球面的主索节点位置图。利用所给的主索节点坐标,可得基准球面的主索节点位置图。
Step3:利用欧式距离公式求同一促动器顶端在基准球面和理想抛物面位置上对应的两个坐标间的距离。
Step4:求解促动器的伸缩量及反射面板数量的最优解。
在照明区域内,当每一个促动器顶端从基准球面移到理想抛物面上的距离小于0.6m时,就是促动器的伸缩量,即反射面完全可以到达理想抛物面;当每一个促动器顶端从基准球面移到理想抛物面上的距离大于0.6m时,促动器的伸缩量只有取0.6m时才能使反射面最贴近理想抛物面。同时可以根据主索节点的个数求出反射面板数量的最优解。
3 反射球面接收比模型的建立与求解
3.1 模型的建立
3.1.1 馈源舱圆盘函数关系式
由理想抛物面顶点坐标Q(-49.254,-36.940,-293.627),馈源舱平面是以焦点P(-26.269,-19.648,-156.601)为几何中心,半径为0.5m的一个圆盘,且该圆盘与垂直,则有:

由于馈源舱面是空间平面,需要将该圆盘还原为垂直XOY平面的初始圆盘方程1W,再根据欧拉角和旋转矩阵变形,可以得到初始圆盘方程1W为:

3.1.2 射入直线函数关系式

3.1.3 反射面方程
每个反射面由3个节点坐标构成,设3点坐标为:

3.1.4 射出直线函数关系式
由于射出信号直线2L与信号射入直线1L关于反射面M对称,设垂直平面的法线方程l为:

又因为直线与平面垂直,所以函数未知数系数之比相等:
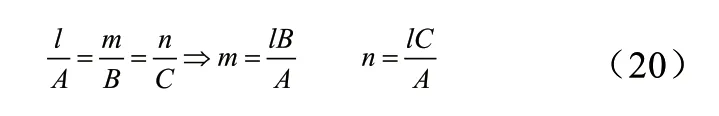
化简得到法线方程l为:
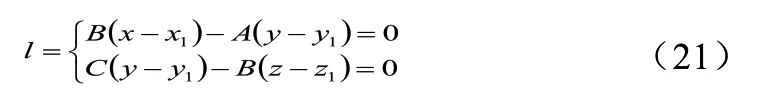
由于已知入射直线方程,则在入射方程上任意取一点m( x '', y'',z''),设在射出直线方程上与m( x '', y'',z'')关于法线方程l的对称点为m'( x ''',y''',z'''),则有:

3.2 模型求解
得到2L后将其与馈源舱圆盘方程 2W联立运行是否有解,如果方程组有解则该点信号可以被馈源舱接收,反之则该点不能。将经过调整伸缩量的点坐标分别代入,N为调整点的总数,设其中有n个点可以被接收。
通过每个节点坐标对应的平面,将得到的可以被接收信号的点坐标与表中信息对比,找出满足3个点都在接收信号点集合内的面,利用矩阵将所有的节点编号转换为数字信息。再将范围内的节点数字信息放在一个集合内。将矩阵中的每一个元素都做一次判断,判断该元素是否在集合内,若在则编码为1,否则为0。最后整理统计一组数据中1的数量,若数量为3则说明这3点所围的反射面板为所求范围内面板。计算结果为,调节后馈源舱的接收比为84.373%,基准反射球面的接收比为87.278%。
