基于期望值最大化的理论何时失效：风险决策中为自己–为所有人决策差异的眼动研究*

刘洪志 李兴珊 李 纾,4 饶俪琳

基于期望值最大化的理论何时失效：风险决策中为自己–为所有人决策差异的眼动研究*

刘洪志3李兴珊1,2李 纾1,2,4饶俪琳1,2

(1中国科学院行为科学重点实验室, 中国科学院心理研究所, 北京 100101) (2中国科学院大学, 北京 100049) (3南开大学周恩来政府管理学院社会心理学系, 天津 300350) (4浙江大学心理与行为科学系, 杭州 310028)

主流的风险决策理论专家发展了一系列基于期望值最大化(expectation-maximization)的理论, 以期捕获所有人的风险决策行为。然而大量证据表明, 这些基于期望值最大化的理论并不能如同描述性理论那样理想地描述单一个体的决策行为。本研究采用眼动追踪技术, 系统考察了个体在为所有人决策与为自己决策时的风险决策行为及信息加工过程的差异。本研究发现, 基于期望值最大化的理论可捕获为所有人决策或为自己多次决策时的情况, 却不能很好捕获个体为自己进行单次决策时的情况。本研究结果有助于理解基于期望值最大化的理论与启发式/非基于期望值最大化的理论的边界, 为风险决策理论的划分和发展提供实证参考。

风险决策, 为所有人决策, 期望值最大化, 为自己–为所有人决策差异, 眼动追踪技术

1 引言

相传有一个关于决策理论专家Howard Raiffa的轶事。Raiffa是贝叶斯决策理论的先驱和决策分析领域的奠基人。1957年, 时任教于哥伦比亚大学的Raiffa教授收到了来自哈佛大学的教职邀请。Raiffa犹豫不决, 便向哥伦比亚大学的系主任寻求建议。讽刺的是, 系主任建议Raiffa应根据他自己所提出的决策分析理论那样进行决策: 分析两个选项的相关维度, 赋予各维度以权重, 再根据期望值算法计算出两选项的总分, 并选择总分更高的学校。然而, Raiffa却回答说: “不, 这是一个严肃的抉择(No, this is a serious decision)。” (见Bazerman et al., 1998)。这则轶事提示我们, 为描述所有人的决策行为所发展出的决策理论不一定适用于描述单一个体的决策。主流的决策理论专家试图为所有面临决策的个体提供普适性的最优决策方案, 并发展出了丰富多样的“加权求和最大化”的决策理论。然而, 当在现实世界中面临真实的决策问题时, 决策者(甚至包括决策理论专家本人)并不愿将这些复杂的加权求和理论付诸实践。受到Raiffa轶事的启发, 本研究旨在探索导致期望值最大化的理论失效的内在原因。

在风险决策领域, 基于期望值最大化(expectation-maximization)理论的发展史, 便可视为Raiffa轶事的演绎史。主流的风险决策理论从未放弃期望值最大化的核心框架, 即假设在风险决策中, 个体会基于概率的权重函数对各选项结果的效用进行加权, 并累加所有加权后的效用值(即获取期望值), 最终选择期望值最大的选项(Kahneman & Tversky, 1979; Payne & Braunstein, 1978; Tversky & Kahneman, 1992)。期望价值(expected value, EV)理论(Bernoulli, 1738)、期望效用(expected utility, EU)理论(von Neumann & Morgenstern, 1947)、预期理论(prospect theory)(Kahneman & Tversky, 1979)等均属于此类理论, 这些理论均假设风险决策是基于加权求和的加工过程做出的(Payne & Braunstein, 1978)。

然而, 大量证据表明主流理论家发展的基于期望值最大化的理论并不能捕获个体(甚至如Raiffa一样的决策专家)的真实风险决策行为。众多研究表明, 个体在风险决策时并未采用基于期望值最大化的理论所假设的认知加工过程, 而是采用基于另一类独特理论取向的简单启发式策略进行决策(Brandstätter et al., 2006; Li, 2004, 2016)。这些启发式理论假设, 个体在风险决策时不必整合选项所有维度的信息以达成决策。许多启发式理论, 如最大值最大启发式(maximax heuristic, MH)(Savage, 1951)、齐当别(equate-to-differentiate, ETD)抉择模型(Li, 2004, 2016; Huang et al., 2021)、占优启发式(priority heuristic)(Brandstätter et al., 2006)等, 均假设个体在风险决策时首先会识别并比较选项间多个维度(或单一维度)的差异, 并基于关键的单一维度进行决策。

主流决策理论家之所以不放弃遵循加权求和计算方式的基于期望值最大化的理论, 或是因为他们从不怀疑这些理论能够准确、理想地捕获到人们的风险决策行为。在发展基于期望值最大化的各种理论时, 理论家往往试图发展出用于计算最优决策方案的数理模型, 使得该方案适用于所有面临这一方案的个体(Baron, 1986)。在本研究中, 我们聚焦于这种为所有人决策(decision-for-everyone)的情况, 即为所有面临该选择的人提供最优方案。此外, 本研究亦关注多次决策(decision-for-self-multiple-play), 即当风险选项会被执行多次时, 个体的风险决策行为(Li, 2003; Su et al., 2013)。本研究认为, 与单次为自己决策(decision-for-self-single-play)的情况不同, 基于期望值最大化的理论或许在描述为所有人决策或多次决策时是行得通的。

我们认为, 基于期望值最大化的理论可以解释为所有人决策和多次决策的情况。与多次风险决策类似, 在为所有人决策的情境中, 个体需要为所有面临选择的人提供最优方案, 即意味着所选择方案将被执行多次。根据大数定律(law of large numbers), 即在大样本中, 随机事件发生的相对频数可近似于事件发生的概率(van der Stoep & Seifert, 1994), 因此如果某一风险决策的重复次数足够多, 那么其决策结果会趋近于期望价值(Klos et al., 2005)。由于在为所有人决策和多次决策的情况下, 风险决策一旦做出便会被执行多次, 因此决策者倾向于将风险选项的可能结果视为可相互补偿的, 并考虑选项的过去统计数据和未来的多种机会, 从而遵循期望值最大化理论所假设的决策策略。相反, 单次为自己决策的情境无法满足基于期望值最大化的理论重复多次的理论需求。因此, 决策者往往倾向于将风险选项视为独特的(Kahneman & Lovallo, 1993), 并认为不同选项的可能结果不可互相补偿(DeKay et al., 2006; DeKay & Kim, 2005), 从而“明智地”忽略其期望值(Kahneman & Lovallo, 1993)。在这种情况下, 个体并不会采用期望策略(即基于期望值最大化的策略), 而更可能采用一些启发式策略(Brandstätter et al., 2006; Li, 2004, 2016)。

现有的行为学和认知神经科学研究一致发现, EV策略已经可以较好描述个体的多次风险决策情境(Klos et al., 2005; Li, 2003; Rao et al., 2013; Su et al., 2013), 这在一定程度上支持了本研究的推断(参见：孙红月等, 2011)。然而, 尽管人们意识到相对于日常生活中为自己决策, 为所有人决策(如政府为所有公民制定应对重大公共卫生突发事件的政策、医生为所有病人制定标准的治疗方案等)其决策质量问题更事关重大、其决策后果所产生的影响力更加深远, 但至今尚鲜有研究检验期望策略(即基于期望值最大化的策略)是否可足够好地描述为所有人做风险决策的情境。此外, 缺乏为所有人决策与为自己决策的差异的了解也阻碍我们理解现实中一些决策冲突发生的潜在机理。以医疗决策为例, 医生为众多患者决策时或采用期望策略以降低“决策噪声” (Kahneman et al., 2021), 而为自己或家人进行医疗决策时可能采取某些启发式策略(Popovic et al., 2019), 这种由于不同决策目标、情境所产生的决策差异或可导致医患关系冲突问题。因此, 考察为所有人决策的特点与心理机制不仅具有理论意义而且具有重要的现实应用价值。

本研究采用组内设计, 检验了个体在为所有人决策情境和多次决策情境中是否采用与为自己决策情境中相同的决策策略。本研究假设, 个体在为所有人决策和多次决策条件下更可能采用期望策略, 而在为自己单次决策条件下更可能采用启发式策略。近年来, 眼动追踪技术被成功用于考察决策的认知加工过程(Brandstätter & Körner, 2014; Liu et al., 2020; Liu et al., 2021; Sui et al., 2020; Zhou et al., 2021; 魏子晗, 李兴珊, 2015)。因此, 本研究采用眼动追踪技术来比较个体在不同决策任务中的信息加工过程, 以检验研究假设。

本研究构建了3个风险决策任务: 为所有人决策任务, 多次决策任务和单次(为自己)决策任务。引入多次决策任务, 是因为鉴于众多研究已经验证个体在多次决策任务中倾向于采用期望策略(Klos et al., 2005; Langer & Weber, 2001; Li, 2003; Sun et al., 2014), 这一任务可用作对照任务以帮助鉴别为所有人决策任务和单次决策任务中个体是否也采用了期望策略。

期望策略与启发式/非期望策略对个体的眼动指标有不同的预测。总的来说, 采用这两种不同策略会影响个体的整体扫视轨迹模式(Zhou et al., 2016)。具体来说, 采用这两种策略会从三方面影响个体的信息搜索与加工: 信息加工的深度、复杂度和方向(Su et al., 2013)。采用期望策略通常需要整合选项的所有可用信息, 采取复杂的计算方法, 进行基于选项的信息搜索; 而采用启发式/非期望策略通常只需要有选择性地使用选项信息, 采取简单的定性比较, 进行基于维度的信息搜索。因此, 如果为所有人决策任务和多次决策任务基于期望策略, 而单次决策任务基于启发式/非期望策略, 那么为所有人决策任务和多次决策任务与单次决策任务在眼动指标上将存在差异。据此, 本研究提出如下假设:

H1: 为所有人决策任务和多次决策任务的扫视轨迹模式的相似性应高于为所有人决策任务和单次决策任务的相似性。

H2: 为所有人决策任务和多次决策任务的信息获取深度和信息加工复杂度应高于单次决策任务, 且比单次决策任务更多采用基于选项的信息搜索模式。

为明确相关眼动指标在实验任务与风险决策之间的解释作用, 本研究进一步检验如下假设:

H3: 眼动指标(即信息获取深度, 信息加工复杂度和信息搜索方向)可中介决策任务对个体的选择是否符合EV预测(EV-consistent choice)的效应。

为进一步检验个体是否采用期望策略或启发式/非期望策略, 研究者通常会基于认知心理学中常用的双分离(double dissociation)逻辑操纵两个影响因素(Brandstätter et al., 2006; Rao et al., 2013; 刘洪志等, 2015; 张阳阳等, 2018)。双分离逻辑指的是: 如果某因素影响任务A的绩效但不影响任务B, 另一因素影响任务B的绩效但不影响任务A, 则表明两任务包含不同的心理过程(Rao et al., 2013)。本研究关注的第一个因素是两选项期望值的差异。有研究发现, 两选项EV差异越大, 基于期望值最大化的理论预测的准确率越高(Brandstätter et al., 2006, 2008)。本研究关注的第2个因素是维度差异。有研究发现, 结果维度的差异可影响启发式/非期望策略的选择行为和认知加工过程(Brandstätter et al., 2006; Rao et al., 2011; Rao et al., 2013; Huang et al., 2021)。因此, 本研究也检验了如下假设。

H4: 结果维度差异的量级(简称结果差异)应当影响单次决策任务的信息加工过程(如信息获取深度), 而选项间EV值差异的量级(简称EV差异)不会有此效应; EV差异应当影响为所有人决策任务和多次决策任务的信息加工过程(如信息加工复杂度), 而结果差异不会有此效应。

2 方法

2.1 被试

采用G*Power软件(version 3.1.9.2)(Faul et al., 2007)计算实验所需样本量。设定统计检验力(1 – β)为95%, 效应量为Cohen’s= 0.32 (参考Su等人(2013)的研究结果), 计算所需样本量为= 46。实验共招募52名大学生被试(男性26人, 平均年龄 = 22.8 ± 3.0周岁)。所有被试视力或矫正视力正常, 且实验前签署了知情同意书。实验结束后被试获得120元人民币的基本报酬及0～45元与实验表现相关的额外奖励。4名被试的数据因眼动追踪数据不完整被删除, 有效被试48人。

2.2 设备

被试的眼动数据通过采样率为1000 Hz的Eye-Link 1000眼动仪(SR Research, Canada)来收集。被试用双眼观看实验刺激, 但只采集右眼的眼动数据。实验刺激呈现于19英寸的CRT显示器上(刷新率为150 Hz), 其分辨率为1024 × 768。为减小头动对眼动轨迹的影响, 实验中采用距离显示器60 cm的腮托固定被试的头部。被试双眼与屏幕边缘的水平视角为37°, 垂直视角为28°。被试通过用一个微软SideWinder手柄按键来对实验刺激做出反应。

2.3 实验材料和程序

2.3.1 实验刺激

本研究建构了108对各包含两个金钱结果的风险选项(见补充材料表S1: https://osf.io/yg67b/), 所有选项只涉及金钱获益。108对选项组成3 (EV差异: 小, 中, 大) × 3 (结果差异: 小, 中, 大)的实验设计, 每种条件包含12对选项。EV差异指的是两选项之间EV值的差异, 分为3个水平: 两选项的EV差异为10, 30和60。每个选项包含一个最好可能结果和一个最差可能结果。两选项在最好可能结果维度的差异分为3个水平: 差异为400, 300和200; 两选项在最差可能结果维度的差异固定为100。

实验采用Brandstätter和Körner (2014)的刺激呈现方式, 以保证被试每次只能单独注视选项的某一信息, 而无法有效感知到相邻信息。具体来说, 每个信息(结果或概率)均被一个边长为3.50°视角、厚度为0.90°视角的正方形所包围, 以防止被试的余光识别到其他相邻信息(Bouma, 1970)。任意相邻两信息的中心距离为5.95°视角, 可保证被试在不发生眼动的情况下只能识别一个条目(Rayner, 2009)。每个选项的结果信息均呈现在其对应概率的左侧(如图1a所示)。选项的呈现位置已平衡, 即EV值较大的选项一半在上侧一半在下侧。

2.3.2 实验任务

本研究构建了3个风险决策任务: 为所有人决策任务, 多次决策任务和单次决策任务。在为所有人决策任务中, 告知被试从两选项中选出最优选项, 假设其所选择的选项将成为所有面临该选择的人的选择——即, 每人都接受相同选择, 但可能面临不同结果。在多次决策任务中, 告知被试选择自己偏爱的选项, 假设其选择的选项将被执行100次。在单次决策任务中, 告知被试选择自己偏爱的选项, 假设其选择的选项只被执行1次。

为进一步激励被试认真完成实验任务, 告知被试他们的额外实验报酬将由其在实验中的表现所决定。在多次决策任务和单次决策任务中, 告知被试在实验结束后会随机选择一次决策, 用一个后台程序来确定结果, 并按照一定比例确定实验报酬。在单次决策任务中, 所选择选项将被执行1次。在多次决策任务中, 所选择选项将被执行100次, 即被试的某一次选择将被后台程序执行100次, 并将结果累加在一个虚拟账户中, 其金额越大, 被试在此任务中的奖励越多。在为所有人决策任务中, 告知被试实验结束后会根据他们是否为所有人选择了最优选项来确定其实验报酬(并未要求被试选择EV值大的选项)。在实验开始前, 告知被试所有实验报酬需在3个任务全部完成后才可发放。

实验采用被试内设计, 每名被试需完成全部3个实验任务, 但被试每次来实验室只完成1个任务, 任意2个实验任务的时间间隔不少于3天。任务顺序在被试间进行了平衡。三个任务所采用的实验刺激在视觉上完全相同(见图1a)。

2.3.3 实验程序

在每个实验任务开始前先进行校准。实验采用9点校准和验证, 最大验证误差为0.5°视角。在初始校准后进行4个练习试次, 以帮助被试熟悉实验刺激的呈现方式及任务要求。正式实验包括108试次, 呈现顺序在被试间进行了平衡。108试次分为3个组块(block), 每个组块有36试次。被试在完成每个组块后可休息1～2分钟。

在每一试次开始时, 屏幕中央会呈现一个圆形注视点作为漂移校准。当被试注视屏幕中央的注视点时, 可通过按键来触发呈现选项刺激。然后被试通过另外两个按键进行选择, 按左键来选择屏幕上侧的选项A, 按右键来选择屏幕下侧的选项B。被试的决策时间不受限制, 一旦做出决策后, 选项刺激将消失, 并呈现1000 ms的空白屏, 随后开始下一试次(详见图1)。在实验过程中不会出现关于选择结果的任何反馈。

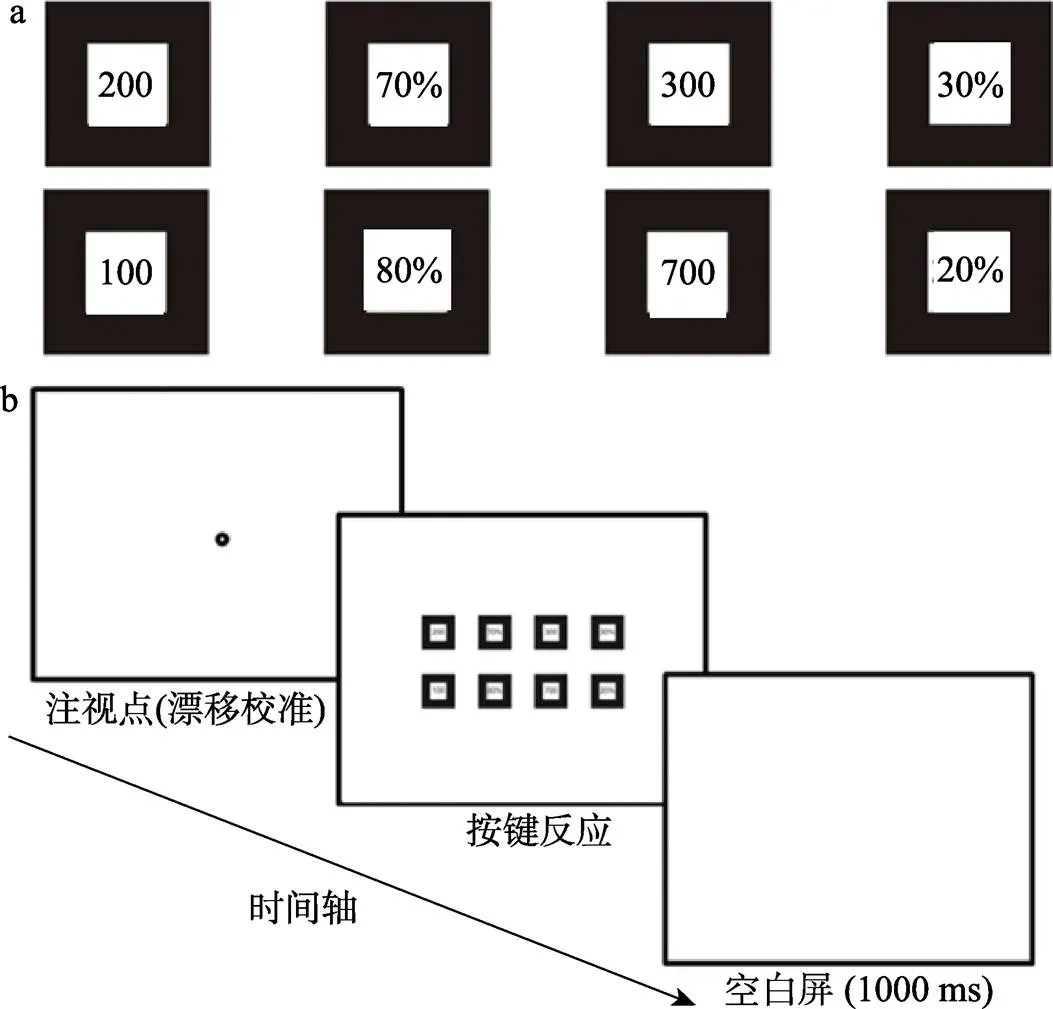
图1 实验刺激及流程。(a) 实验刺激呈现方式。 (b) 试次程序及时间。

2.4 模型预测

基于被试的选择计算不同决策理论预测的准确率。本研究采用的理论模型包括: (1) 3个基于期望值最大化的理论, 包括EV理论(Bernoulli, 1738), EU理论(von Neumann & Morgenstern, 1947)和累积预期理论(cumulative prospect theory, CPT) (Tversky & Kahneman, 1992), 以及(2) 3个启发式/非基于期望值最大化的理论, 包括齐当别抉择模型(Li, 2004, 2016), 最大值最大启发式(Brandstätter et al., 2006; Savage, 1951)和计数启发式(tallying heuristic, TH) (Gigerenzer, 2004)。以上模型的决策规则总结见表1。本研究检验了以上模型对被试选择的预测力。

2.5 眼动数据分析

眼动数据采用软件Eyelink Data Viewer (SR Research, Canada)来分析。注视点(fixation)定义为两次眼跳之间眼睛位置相对稳定的一段时间, 短于50 ms的注视点在数据分析时被剔除。将实验刺激划为8个互不重叠的等大(5.90° × 5.90°视角)矩形兴趣区(regions of interest, ROIs)。为了检验研究假设, 本研究分析了扫视路径模式, 各兴趣区的注视次数, 不同兴趣区之间的眼跳次数, 以及所有兴趣区的平均注视时长。同时, 为检验被试在三个任务中的认真程度是否相同, 本研究计算了每个试次的最大瞳孔直径, 因为瞳孔大小可作为反映个体在实验任务中认真程度的有效指标(Hopstaken et al., 2015)。

3 结果

实验总计15552试次, 其中2试次因眼动追踪失败而在数据分析时被剔除。

以试次中的最大瞳孔直径为因变量, 以实验任务为自变量的单因素重复测量方差分析发现, 实验任务的主效应不显著,(2, 94) = 2.20,= 0.116, 表明被试在三个任务中的认真程度并无显著差异。

3.1 行为结果

3.1.1 模型预测

以模型预测准确率为因变量, 做3 (任务) × 6 (模型)的重复测量ANOVA。结果发现, 任务的主效应显著,(2, 94) = 31.30,< 0.001, η2p= 0.40; 模型的主效应显著,(5, 235) = 201.50,< 0.001, η2p= 0.81; 交互作用显著,(10, 470) = 31.20,< 0.001, η2p= 0.40。事后检验发现, 对于为所有人决策任务和多次决策任务, EV、EU和CPT的预测准确率显著高于其他模型(s ≥ 9.07,s < 0.001); 对于单次决策任务, EV、EU、TH、ETD和MH的预测准确率均无显著差异(s ≤ 2.56,s > 0.502), 而CPT的预测准确率显著高于其他模型(s ≥ 5.57,s < 0.001), 见图2。

3.1.2 决策时间

决策时间(ms)进行了自然对数转换。单因素重复测量的方差分析表明, 决策任务的主效应显著,(2, 94) = 5.39,= 0.006, η2p= 0.10。事后检验发现, 单次决策任务的决策时间(= 8.75, 95% CI = [8.63, 8.87])短于为所有人决策任务(= 8.91, 95% CI = [8.79, 9.03],(94) = 2.83,= 0.015)和多次决策任务(= 8.91, 95% CI = [8.78, 9.04],(94) = 2.86,= 0.014), 但为所有人决策任务和多次决策任务的决策时间没有显著差异,(94) = 0.02,= 1.000。

模型预测结果表明, 基于期望值最大化的理论与启发式/非基于期望值最大化的理论在单次决策任务中的预测力均表现不够好。基于期望值最大化的理论(尤其是EV和EU理论)在为所有人决策任务和多次决策任务中的预测力优于启发式理论(事实上, 启发式理论并未宣称可预测人们在为所有人决策任务和多次决策任务中的选择)。这些结果表明, 相比于单次决策任务, 被试在为所有人决策任务和多次决策任务中更可能采用EV或EU理论所假设的策略。由于期望策略通常比启发式/非期望策略需要更长的决策时间(Rao et al., 2011; Su et al., 2013), 本研究关于决策时间的结果亦表明相比于单次决策任务, 被试在为所有人决策任务和多次决策任务中更可能采用期望策略。此外, 本研究所发现的单次决策任务与多次决策任务模型预测与决策时间上的差异, 亦重复了Su等人(2013)研究中所揭示的结果模式。

表1 六个预测模型的决策规则总结

图2 在(a)为所有人决策任务, (b)多次决策任务和(c)单次决策任务三个任务中基于期望值最大化的理论与启发式/非基于期望值最大化的理论对选择的预测准确率。误差棒表示均值的标准误。

3.2 扫视路径分析

为了检验为所有人决策任务和多次决策任务中的扫视路径模式是否异于单次决策任务(H1), 本研究采用Zhou等人(2016)介绍的扫视路径分析法(scanpath analysis)。当个体在某一认知阶段时观看屏幕, 即可产生一个相对固定的“路径” (path)。这一路径往往具有特定模式, 因此称为“扫视路径” (scanpath; Noton & Stark, 1971)。扫视路径分析可为行为决策理论的认知加工过程提供更清晰、直接的证据(Ashby et al., 2016)。通常使用相似性分数来比较风险决策中两个扫视路径的相似性程度(Zhou et al., 2016), 相似性分数值越大, 意味着两个扫视路径越相似。本研究采用基于Needleman-Wunsch (N-W)算法(Needleman & Christian, 1970)的ScanMatch软件包(Cristino et al., 2010), 来计算不同扫视路径之间的相似性分数, 设置参数为Cristino等(2010)建议的默认值。与只考虑注视点序列的传统字符编辑(string-editing)算法相比, N–W算法可进一步考虑注视序列中的注视点时长, 将注视点基于时长进行分割, 从而提高注视序列相似性比较的灵敏度, 此外, 这一算法亦可基于刺激的兴趣区进行编码(Zhou et al., 2016)。本研究分别计算了每个被试的任务内和任务间相似性分数。

单次决策任务的任务内相似性分数(= 0.465, 95% CI = [0.454, 0.476])显著低于为所有人决策任务(= 0.485, 95% CI = [0.468, 0.502],(47) = 2.66,= 0.011, Cohen’s= 0.38)和多次决策任务(= 0.484, 95% CI = [0.470, 0.498],(47) = 3.35,= 0.002, Cohen’s= 0.48)的相似性分数, 而后两者没有显著差异,(47) = 0.09,= 0.933, Cohen’s= 0.01, 见图3。该结果表明, 单次决策任务的扫视路径模式的内部一致性低于为所有人决策任务和多次决策任务, 这暗示相比于单次决策任务, 为所有人决策和多次决策任务的扫视路径同质性更高, 其决策策略更一致。

对于三个决策任务, 任务内相似性分数均高于任务间相似性分数(s ≥ 5.56,s < 0.001, Cohen’ss ≥ 0.80), 表明被试在三个决策任务中的扫视路径模式均存在差异。进一步分析发现, 为所有人决策任务和多次决策任务的任务间相似性分数(= 0.454, 95% CI = [0.439, 0.469])高于为所有人决策任务和单次决策任务的任务间相似性分数(= 0.432, 95% CI = [0.417, 0.446],(47) = 3.46,= 0.001, Cohen’s050)以及多次决策任务和单次决策任务的任务间相似性分数(= 0.434, 95% CI = [0.420, 0.449],(47) = 3.53,< 0.001, Cohen’s= 051), 但是后两个相似性分数没有显著差异,(47) = 0.46,= 0.645。该结果表明, 为所有人决策任务与多次决策任务的扫视路径模式较于单次决策任务更为相似。

总的来说, 相似性分数的结果表明, 虽然三个决策任务的扫视路径模式各不相同, 但是为所有人决策任务和多次决策任务的扫视路径模式较于单次决策任务更为相似, 支持了H1。

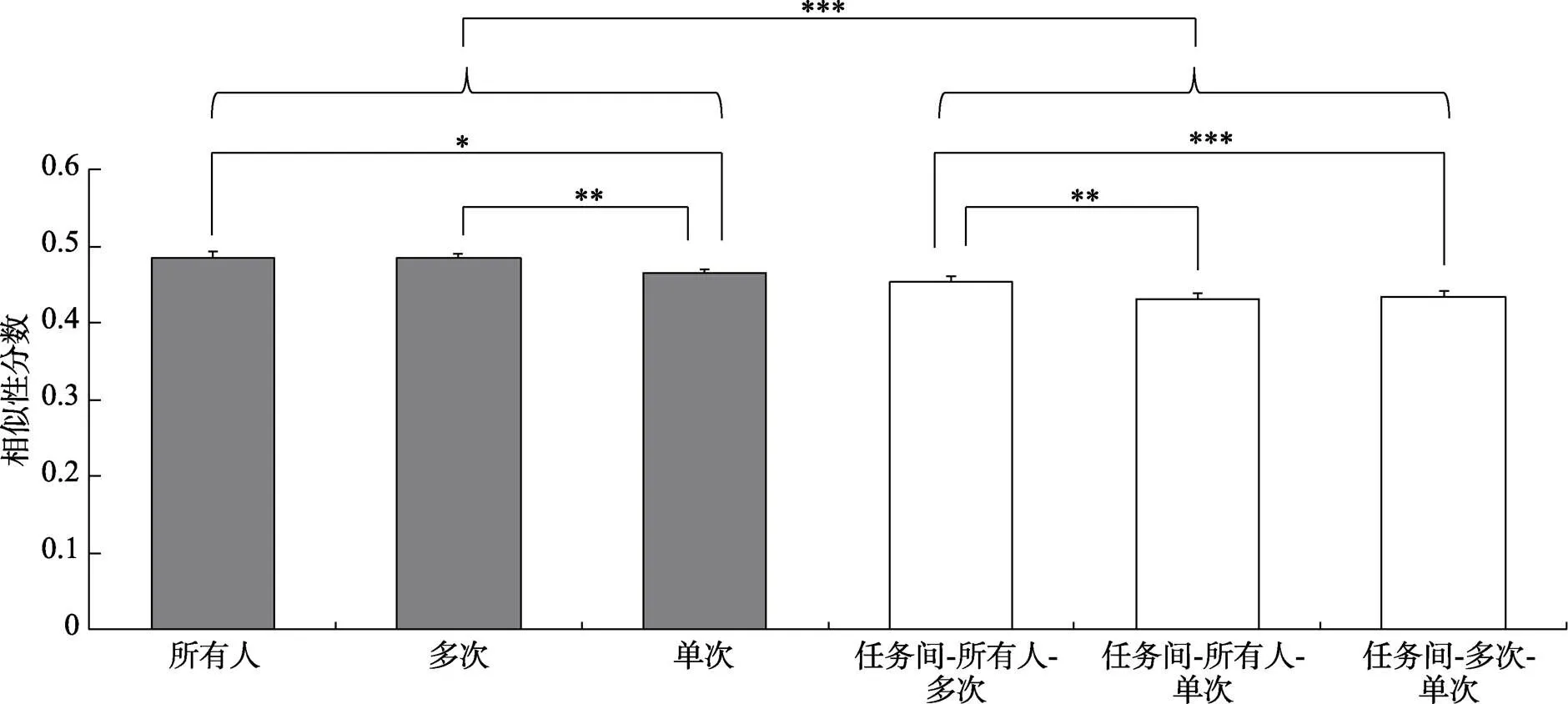
图3 三个任务的任务内与任务间相似性分数。

注：误差棒表示均值的标准误。***< 0.001,**< 0.01,*< 0.05。

3.3 眼动指标

为检验H2, 本研究考察了以下眼动指标。(1) 与前人研究一致(Payne & Braunstein, 1978; Su et al., 2013), 本研究用信息搜索比例(percentage of total information searched, PTIS)来测量各任务的信息获取深度。(2) 本研究用平均注视时长(mean fixation duration, MFD)来测量决策过程中信息加工的复杂度。单个注视点的时长会随着信息加工复杂度的升高而增大(Velichkovsky et al., 2002)。(3) 本研究用基于选项/基于维度的搜索指数(search measure index, SMI)和最好结果间眼跳比例(proportion of the saccades between the two best outcomes, PSTB)来衡量信息搜索方向是基于选项或基于维度的程度(Böckenholt & Hynan, 1994; Pachur et al., 2013; Su et al., 2013)。SMI越大, 表示基于选项的眼跳模式越占优(Liu et al., 2021; Su et al., 2013)。如果被试在风险决策中采用期望策略, 那么相比于采用启发式/非期望策略, 其PTIS、MFD和SMI值应更高, PSTB值应更低。

分别以PTIS、MFD、SMI和PSTB为因变量, 构建3 (实验任务) × 3 (EV差异) × 3 (结果差异)的重复测量ANOVA, 结果如表2所示。

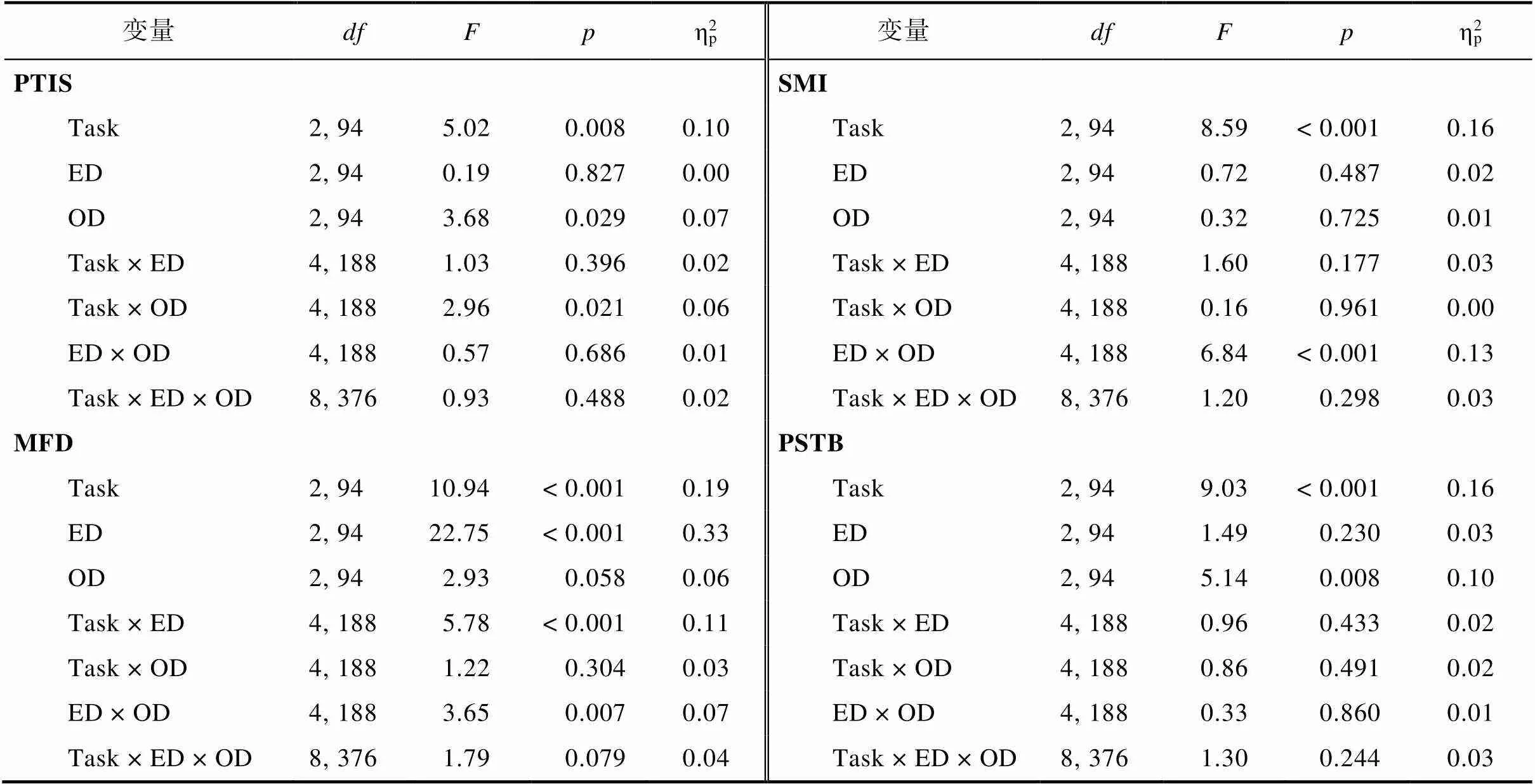
表2 以实验任务、EV差异、结果差异为自变量, 以PTIS、MFD、SMI和PSTB为因变量的方差分析结果

注: Task表示实验任务, ED (EV difference)表示EV差异, OD (outcome difference)表示结果差异。

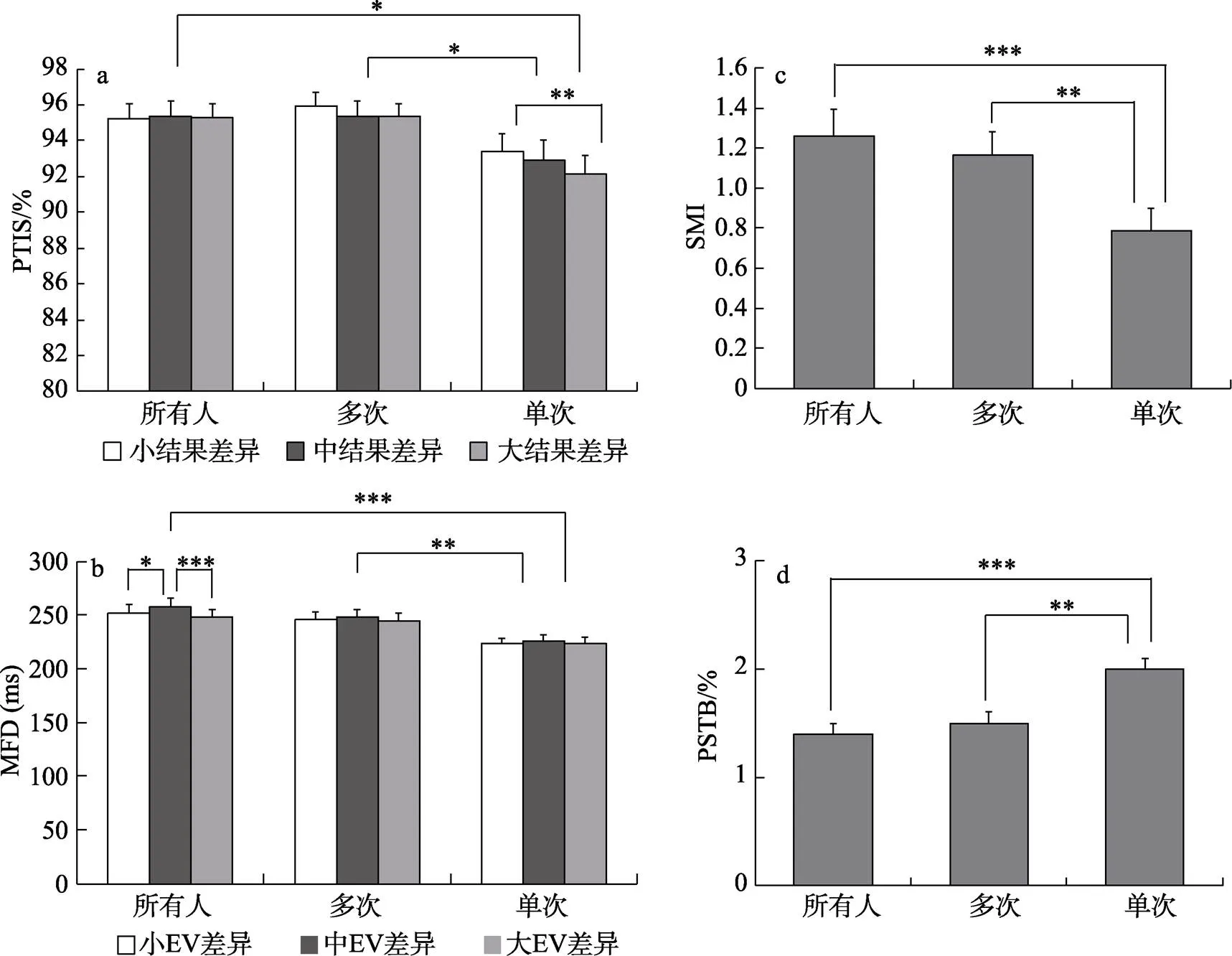
图4 眼动指标结果。(a) PTIS指标结果。(b) MFD指标结果。(c) SMI指标结果。(d) PSTB指标结果。

注：误差棒表示均值的标准误。***< 0.001,**< 0.01,*< 0.05。

结果发现, 实验任务在4个眼动指标上均存在显著的主效应(见表2)。事后检验发现: (1) 单次决策任务中的PTIS(= 92.8%, 95% CI = [91.0%, 94.5%])显著低于多次决策任务(= 95.6%, 95% CI = [93.8%, 97.3%],(94) = 2.88,= 0.014)和为所有人决策任务(= 95.3%, 95% CI = [93.7%, 97.1%],(94) = 2.59,= 0.029) (见图4a); (2) 单次决策任务中的MFD (= 224 ms, 95% CI = [211, 238] ms)显著低于多次决策任务(= 246 ms, 95% CI = [233, 259] ms,(94) = 3.48,= 0.002)和为所有人决策任务(= 252 ms, 95% CI = [239, 265] ms,(94) = 4.45,< 0.001) (见图4b); (3) 单次决策任务中的SMI (= 0.79, 95% CI = [0.55, 1.03])显著低于多次决策任务(= 1.17, 95% CI = [0.93, 1.40],(94) = 3.14,= 0.006)和为所有人决策任务(= 1.26, 95% CI = [1.02, 1.50],(94) = 3.92,< 0.001) (见图4c); (4)单次决策任务中的PSTB (= 2.0%, 95% CI = [1.7%, 2.2%])显著高于多次决策任务(= 1.5%, 95% CI = [1.3%, 1.8%],(94) = 3.24,= 0.005)和为所有人决策任务(= 1.4%, 95% CI = [1.2%, 1.7%],(94) = 4.00,< 0.001) (见图4d)。在以上4个指标上, 均未发现多次决策任务和为所有人决策任务存在显著差异。

ANOVA结果发现, 实验任务与结果差异在PTIS这一变量上存在显著交互作用(见表1)。简单效应分析发现, 在单次决策任务中, 大结果差异条件下的PTIS显著低于小结果差异条件,(277) = 4.04,= 0.002。为所有人决策任务和多次决策任务在PTIS指标上无显著差异。本研究在PTIS指标上关于结果差异只影响单次决策任务的发现支持了H4。

ANOVA结果还发现, 实验任务与EV差异在MFD指标上存在显著交互作用(见表1)。简单效应分析发现, 在为所有人决策任务中, 大EV差异条件下的MFD显著低于中EV差异条件((281.9) = 7.65,< 0.001)和小EV差异条件((281.9) = 3.28,= 0.031)1与预期不符的是, 中EV差异条件的MFD显著大于小EV差异条件。这一结果可能是由于小EV差异条件的计算难度低于中EV差异条件。我们猜测, 概率为10% (或金钱结果为100元)的选项计算期望价值的难度低于其他概率(或金钱结果)的选项。事后观察发现, 小EV差异条件比中EV差异条件包含更多低计算难度的选项(小EV差异条件有26个选项是低计算难度, 中EV差异条件有18个选项是低计算难度)。分析发现, 在控制计算难度后, 在为所有人决策任务中小、中EV差异条件的MFD没有显著差异(F(1, 47) = 1.79, p = 0.187), 这在一定程度上支持了我们的猜测。。多次决策任务和单次决策任务在MFD指标上无显著差异。本研究在MFD指标上关于EV差异只影响为所有人决策任务的发现在一定程度上支持了H4。

以上结果暗示, 相比于多次决策任务和为所有人决策任务, 被试在单次决策任务中的信息获取深度更低, 信息加工复杂度更低, 更可能采用基于维度的信息搜索模式。这些结果表明, 个体在单次决策任务中进行风险决策时更可能采用了启发式/非期望策略进行决策, 而在为所有人决策任务和多次决策任务中更符合期望策略的加权求和加工过程。

3.4 中介分析

为检验H3, 本研究检验了眼动指标是否中介了决策任务对个体的选择是否符合EV预测的效应。设定因变量为选择是否符合EV预测(选择EV较大选项记为1, 否则记为0)。本研究采用SPSS的MEMORE (Montoya & Hayes, 2017)软件包中的平行多中介变量模型来检验决策任务通过一系列平行中介变量进而影响个体的选择是否符合EV预测的效应。这一模型可允许中介变量之间存在相关性, 且能够估计控制其他中介变量的效应之后的各中介变量的间接效应。由于MEMORE软件包只允许放入2水平的组内条件, 因此本研究构建了2个中介分析, 即分别检验两类决策任务(单次决策任务 vs. 为所有人决策任务/单次决策任务 vs. 多次决策任务)通过上文提到的眼动指标对个体的选择是否符合EV预测的影响。基于5000次bootstrap抽样生成95%置信区间(在下文中括号中报告)。

单次决策任务vs. 为所有人决策任务。中介分析结果如图5a所示。决策任务通过以下4个眼动指标对个体的选择是否符合EV预测的间接效应显著: PTIS (11= 0.008 [0.005, 0.012]), MFD (22= 0.021 [0.013, 0.028]), SMI (33= 0.014 [0.009, 0.018]), 以及PSTB (44= 0.006 [0.004, 0.008])。决策任务对因变量的总效应显著(= 0.31 [0.29, 0.32],< 0.001), 直接效应也显著(’ = 0.26 [0.24, 0.28],< 0.001), 说明在控制以上中介变量后, 决策任务仍然能够解释因变量的变异(见图5a)。对各间接效应进行配对检验发现, MFD对因变量的贡献显著高于PTIS (22−11= 0.013 [0.004, 0.020])和PSTB (22−44= 0.015 [0.007, 0.023]), SMI对因变量的贡献显著高于PSTB (33−44= 0.008 [0.002, 0.013])。MFD与SMI的贡献无显著差异(33−22= −0.007 [−0.016, 0.002])。

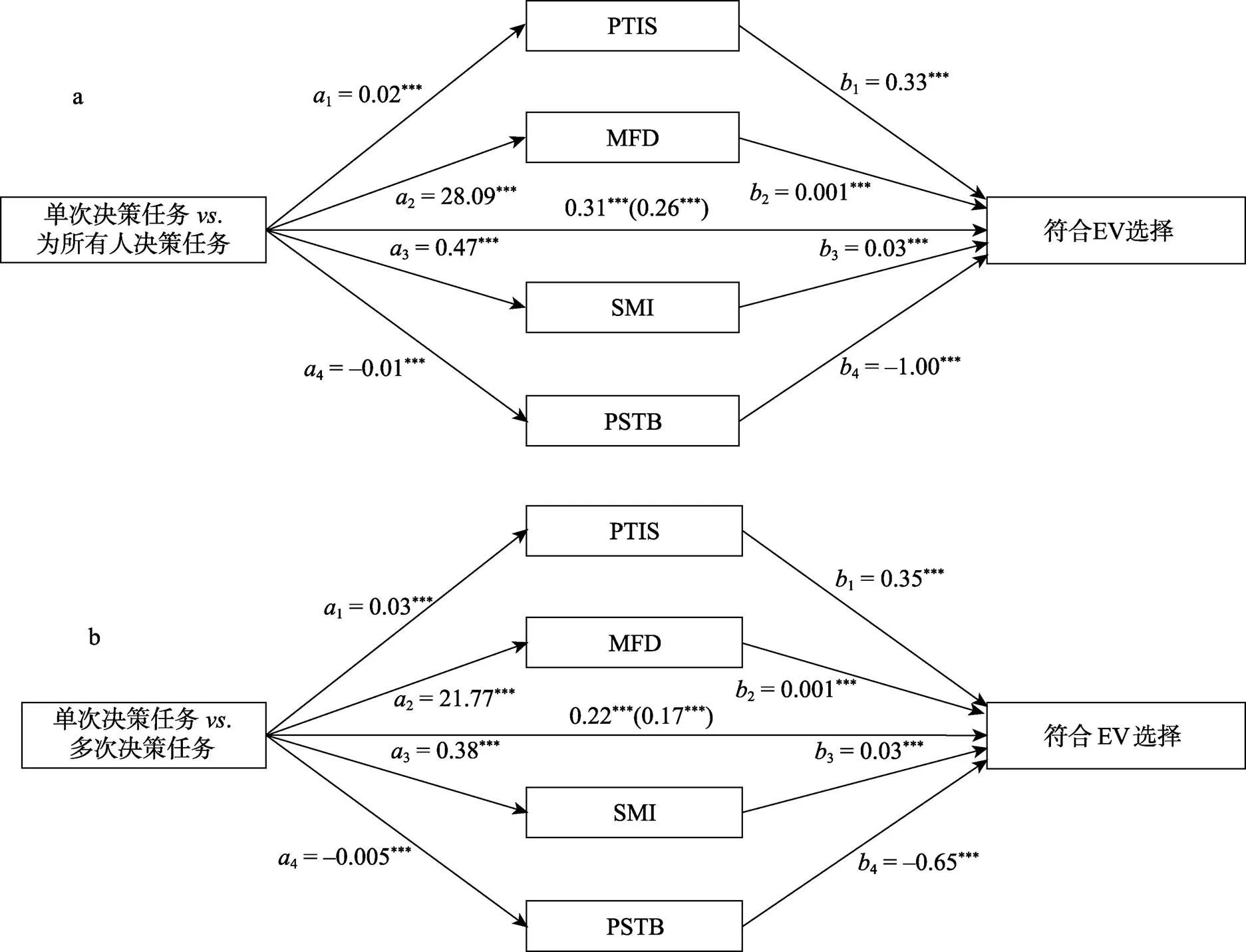
图5 中介分析结果。(a) 决策任务(单次决策任务 vs. 为所有人决策任务)通过眼动指标对个体的选择是否符合EV预测的中介效应。(b) 决策任务(单次决策任务vs. 多次决策任务)通过眼动指标对个体的选择是否符合EV预测的中介效应。***p < 0.001。

单次决策任务vs.多次决策任务。中介分析结果如图5b所示。决策任务通过以下4个眼动指标对个体的选择是否符合EV预测的间接效应显著: PTIS (11= 0.010 [0.006, 0.014]), MFD (22= 0.030 [0.023, 0.036]), SMI (33= 0.012 [0.008, 0.016]), 以及PSTB (44= 0.003 [0.001, 0.005])。决策任务对因变量的总效应显著(= 0.22 [0.21, 0.24],< 0.001), 直接效应也显著(’ = 0.17 [0.15, 0.19],< 0.001), 说明在控制以上中介变量后, 决策任务仍然能够解释因变量的变异(见图5b)。对各间接效应进行配对检验发现, MFD对因变量的贡献显著高于其他三个指标 (22−11= 0.020 [0.012, 0.028],22−33= 0.018 [0.010, 0.026],22−44= 0.027 [0.020, 0.034]), PTIS和SMI对因变量的贡献显著高于PSTB (11−44= 0.007 [0.002, 0.011],33−44= 0.009 [0.004, 0.014])。

与研究假设一致, 中介分析结果发现眼动指标能够中介决策任务对个体的选择是否符合EV预测的效应。在4个眼动指标中, MFD (反映信息加工复杂度的指标)和SMI (反映信息搜索方向的指标)的中介效应最强。相比于单次决策任务, 在多次决策任务和为所有人决策任务中, 被试的信息搜索深度和信息加工复杂度更高、更多采用基于选项的信息搜索模式, 从而导致其更可能选择EV值较大的选项。

4 讨论

关于风险决策是基于期望策略还是启发式/非期望策略的争论至今尚未完美解决(Pachur et al., 2013)。本研究基于过程检验的视角, 采用眼动追踪技术探索了基于期望值最大化的理论与启发式/非基于期望值最大化的理论的边界。

本研究的行为和眼动分析结果总结见图6。行为结果揭示, 相比于单次决策任务, 在为所有人决策任务和多次决策任务中, 被试的选择符合EV和EU理论预测的比例更大, 且需要更长时间进行决策。此外, 眼动指标结果揭示: (1)为所有人决策任务和多次决策任务的扫视路径模式更相似, 且显著不同于单次决策任务; (2)为所有人决策任务和多次决策任务的信息获取深度高于单次决策任务, 且结果差异大小只影响单次决策任务中的信息获取深度; (3)为所有人决策任务和多次决策任务的信息加工复杂度高于单次决策任务, 且EV差异大小只影响为所有人决策任务的信息加工复杂度; (4)相比于单次决策任务, 被试在为所有人决策任务和多次决策任务中更多采用基于选项的信息搜索模式; (5)眼动指标中介了决策任务对选择是否符合EV预测的效应。总之, 行为和眼动指标结果均表明, 相比于单次决策任务, 被试在为所有人决策任务和多次决策任务中更可能采用期望策略。

图6 行为和眼动指标结果总结。

注: 相比于启发式理论, 基于期望值最大化的理论预测个体的选择符合EV预测比例更大, 反应时更长, 信息获取深度更高, 信息加工复杂度更高, 更多采用基于选项的信息搜索方向。

回到前文提到的关于“为什么主流理论家不放弃基于期望值最大化的理论”这一问题。我们以为, 或许是因为有两个信念支撑着这些理论家对基于期望值最大化的理论不离不弃: 一是为发展出用于描述所有人的决策理论而诞生的基于期望值最大化的理论确实能够描述为所有人决策的情境; 二是理论家默认单一个体是包含在所有人中的子集。由此推论, 基于期望值最大化的理论最终当可捕获每个个体的风险决策行为。

针对第一个信念, 本研究从过程检验的视角为期望法则的优美公式符合个体为所有人做风险决策提供了眼动的支持证据。考虑到在大数定律中, “多次”和“多人”的意义相通, 本研究的这一观点同样被多次决策任务中的发现所支持。而以往众多或结果导向或过程导向的研究, 有专注于验证基于期望值最大化的理论可否描述“为自己”的实际风险决策(Brandstätter & Körner, 2014; Li, 2004; Pachur et al., 2013; Rao et al., 2013; Sun et al., 2014), 有专注于验证基于期望值最大化的理论可否描述“为他人”的实际风险决策(Beisswanger et al., 2003; Hsee & Weber, 1997; Mengarelli et al., 2014; Polman, 2012), 但尚没有研究收集“为所有人”决策的证据, 以验证基于期望值最大化的理论可否描述“为所有人”的实际风险决策。本研究发现, 个体在“为所有人”做决策时, 还真像Raiffa教授故事中的系主任所建议的那样, 会进行加权求和并计算总分的算计。

针对第二个信念, 主流理论家会想当然地认为: 为描述所有人(全集)的决策行为发展而来的基于期望值最大化的理论也就一定能够描述包含于所有人中的单个人(子集)的决策行为。然而, 本研究的行为和眼动指标结果首次向世人展现: 为自己决策与为所有人决策是不同的。为自己决策是一回事, 为所有人决策是另外一回事。因此, 理论家为所有人发展出的基于期望值最大化的理论不见得适用于描述单一个体做决策的情况。本研究这首次公布于众的“所有人–单个人”的差异内隐地提示, 基于期望值最大化的理论在为自己决策时行不通的原因可能是, 全集(所有人)和子集(单个人)之间的默认兼容性或是不存在的。正是在这最不可能出现裂痕的环节上出现了不易察觉的裂缝, 才使得基于期望值最大化的理论“莫名其妙”地失效了。

当重新审视帕斯卡和费马提出来的期望价值理论, 本研究发现有两点值得读者深思。第一, 他们发展EV理论的初衷, 是为赌徒(而非为自己)的赌金分配问题提供一个最优方案, 该方案对任何一个面临该问题的人都适用(Durrett, 2010; Vinod & Reagle, 2004)。与帕斯卡和费马的本意相符, 本研究的行为和眼动结果揭示, 在多人、多次决策条件下比在为自己决策条件下更符合EV策略, 表明帕斯卡和费马的EV理论确实能够捕获为所有人的风险决策。第二, 本研究发现, 在为所有人决策的时候, EV理论已能足够准确地预测人们的风险决策(在为所有人决策任务中, EV理论的预测准确率高达89%), 但是在单次决策任务中, 尚不能够准确地预测人们的风险决策(在单次决策任务中, EV理论的预测准确率仅为58%), 这表明在描述个体为所有人做出的决策时, 简单的EV理论似乎已经足矣。值得指出的是, 虽然在单次决策任务中, CPT的预测准确率(= 72%)显著高于其他模型, 但是这一预测力是采用极大化正确率的方法进行参数估计得出的, 使得该模型在预测正确率上相较于其他模型具有较大优势, 同时牺牲了模型的简约性。此外, 也有研究者质疑CPT是否属于期望值最大化的理论, 例如有研究者发现CPT也可很好地适配由启发式模型所生成的决策数据模式(Pachur et al., 2017)。

本研究对风险决策理论的划分提出了新的见解。从EV理论诞生之日起, 期望家族理论一直因为其无法描述个体的实际风险决策(即, 屡屡应付不了不能解释的悖论, 如圣彼得堡悖论、艾勒悖论以及其他新的风险决策悖论(Birnbaum, 2008))而被迫不断修改。传统的EV理论被修正为EU理论(von Neumann & Morgenstern, 1947), SEU理论(Savage, 1954), 加权效用模型(Edwards, 1962), 等级相关效用模型(Quiggin, 1982), 等级和符号相关效用模型(Luce & Fishburn, 1991), 以及第三代预期理论(Schmidt et al., 2008), 等等。这种不断修正的灵魂可反映于Tversky在一封审稿信中的评论: “决策过程中任何明确的选择法则都可以描述成某个函数的最大化。因此, 问题不在于选择过程是否被描述成一个最大化的过程, 而是究竟哪个函数被最大化了” (Tversky原信见Li, 2016, pp. 68–69)。但是, 这种从未停止的修正反而暗示, 至今还没有一个基于期望值最大化的理论能够完美描述个体的实际风险决策行为。由于基于期望值最大化的理论表现不佳, 目前理论界已经无奈地把决策理论分为规范性理论(normative theories)和描述性理论(descriptive theories) (Baron, 2008)两类。换句话说, 理论家不得不给基于期望值最大化的理论一个规范性理论的名分却包容它无法描述个体真实的风险决策行为。与规范性理论的普遍认可的概念有出入, 本研究发现提示, 作为最简单、最原始的规范性理论, EV理论反而不经修正其客观概率和客观结果就能够完美地描述个体为所有人决策时的实际风险决策行为。

或许, 如果要求一个理论能够描述个体为自己决策时的实际风险决策行为, 当下迫切要做的不是继续修正基于期望值最大化的理论, 而是从非补偿性的、非期望值最大化的角度来发展、完善启发式/非期望的决策理论。

5 结论

本文通过眼动实验, 考察了个体在为所有人决策任务、多次决策任务和单次决策任务中的行为和眼动指标, 得到如下结论: (1) 相比于单次决策任务, 个体在多次决策任务和为所有人决策任务中更可能采用EV策略, 其决策时间更长。(2) 就扫视轨迹模式而言, 为所有人决策任务和多次决策任务的相似性, 高于为所有人决策任务和单次决策任务的相似性。(3) 眼动指标可中介决策任务对个体选择是否符合EV预测的效应。(4) 结果差异影响单次决策任务的信息加工过程, EV差异影响为所有人决策任务的信息加工过程。总体结果表明, 基于期望值最大化的理论可捕获为所有人决策时的行为, 但不能捕获为自己决策时的行为。这些发现揭示了基于期望值最大化的理论与启发式/非基于期望值最大化的理论的边界, 为风险决策理论的划分和发展提供实证参考。

Ashby, N. J. S., Johnson, J. G., Krajbich, I., & Wedel, M. (2016). Applications and innovations of eye-movement research in judgment and decision making.(2-3), 96–102.

Böckenholt, U., & Hynan, L. S. (1994). Caveats on a process-tracing measure and a remedy.(2), 103–117.

Baron, J. (1986). Tradeoffs among reasons for action.(2), 173–195.

Baron, J. (2008).(4th ed.). Cambridge, England: Cambridge University Press.

Bazerman, M. H., Tenbrunsel, A. E., & Wade-Benzoni, K. (1998). Negotiating with yourself and losing: Making decisions with competing internal preferences.(2), 225–241.

Beisswanger, A. H., Stone, E. R., Hupp, J. M., & Allgaier, L. (2003). Risk taking in relationships: Differences in deciding for oneself versus for a friend.(2), 121–135.

Bernoulli, D. (1738). Specimen theoriae novae de mensura sortis [Exposition of a new theory on the measurement of risk]., 175–192.

Birnbaum, M. H. (2008). New tests of cumulative prospect theory and the priority heuristic: Probability-outcome tradeoff with branch splitting.(4), 304–316.

Bouma, H. (1970). Interaction effects in parafoveal letter recognition.(5241), 177–178.

Brandstätter, E., Gigerenzer, G., & Hertwig, R. (2006). The priority heuristic: Making choices without trade-offs.(2), 409–432.

Brandstätter, E., Gigerenzer, G., & Hertwig, R. (2008). Risky choice with heuristics: Reply to Birnbaum (2008), Johnson, Schulte-Mecklenbeck, & Willemsen (2008) and Rieger & Wang (2008).(1), 281–289.

Brandstätter, E., & Körner, C. (2014). Attention in risky choice., 166–176.

Cristino, F., Mathot, S., Theeuwes, J., & Gilchrist, I. D. (2010). ScanMatch: A novel method for comparing fixation sequences.(3), 692–700.

DeKay, M. L., Hershey, J. C., Spranca, M. D., Ubel, P. A., & Asch, D. A. (2006). Are medical treatments for individuals and groups like single-play and multiple-play gambles?(2), 134–145.

DeKay, M. L., & Kim, T. G. (2005). When things don't add up: The role of perceived fungibility in repeated-play decisions.(9), 667–672.

Durrett, R. (2010).(4th ed.). New York: Cambridge University Press.

Edwards, W. (1962). Subjective probabilities inferred from decisions.(2), 109–135.

Faul, F., Erdfelder, E., Lang, A. G., & Buchner, A. (2007). G*Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences.(2), 175–191.

Gigerenzer, G. (2004). Fast and frugal heuristics: The tools of bounded rationality. In D. Koehler & N. Harvey (Eds.),(pp. 62–88). Oxford, United Kingdom: Blackwell.

Hopstaken, J. F., van der Linden, D., Bakker, A. B., & Kompier, M. A. (2015). A multifaceted investigation of the link between mental fatigue and task disengagement.(3), 305–315.

Hsee, C. K., & Weber, E. U. (1997). A fundamental prediction error: Self–others discrepancies in risk preference.(1), 45–53.

Huang, Y., Shen, S., Yang, S., Kuang, Y., Li, Y., & Li, S. (2021). Asymmetrical property of the subproportionality of weighting function in prospect theory: Is it real and how can it be achieved?(10), 1928.

Kahneman, D., Sibony, O., & Sunstein, C. R. (2021).. Glasgow, Scotland: William Collins Publishers.

Kahneman, D., & Lovallo, D. (1993). Timid choices and bold forecasts: A cognitive perspective on risk taking.(1), 17–31.

Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk.(2), 263–292.

Klos, A., Weber, E. U., & Weber, M. (2005). Investment decisions and time horizon: Risk perception and risk behavior in repeated gambles.(12), 1777–1790.

Langer, T., & Weber, M. (2001). Prospect theory, mental accounting, and differences in aggregated and segregated evaluation of lottery portfolios.(5), 716–733.

Li, S. (2003). The role of expected value illustrated in decision-making under risk: Single-play vs multiple-play.(2), 113–124.

Li, S. (2004). A behavioral choice model when computational ability matters., 147–163.

Li, S. (2016).. Shanghai, China: East China Normal University Press.

Liu, H. Z., Jiang, C. M., Rao, L. L., & Li, S. (2015). Discounting or priority: Which rule dominates the intertemporal choice process?(4), 522–532.

[刘洪志, 江程铭, 饶俪琳, 李纾. (2015). “时间折扣”还是“单维占优”？——跨期决策的心理机制.(4), 522–532.]

Liu, H. Z., Wei, Z. H., & Li, P. (2021). Influence of the manner of information presentation on risky choice., 605206.

Liu, H. Z., Zhou, Y. B., Wei, Z. H., & Jiang, C. M. (2020). The power of last fixation: Biasing simple choices by gaze- contingent manipulation., 103106.

Luce, R. D., & Fishburn, P. C. (1991). Rank-and sign- dependent linear utility models for finite first-order gambles.(1), 29–59.

Mengarelli, F., Moretti, L., Faralla, V., Vindras, P., & Sirigu, A. (2014). Economic decisions for others: An exception to loss aversion law.(1), e85042.

Montoya, A. K., & Hayes, A. F. (2017). Two-condition within- participant statistical mediation analysis: A path-analytic framework.(1), 6–27.

Needleman, S. B., & Wunsch, C. D. (1970). A general method applicable to the search for similarities in the amino acid sequence of two proteins.(3), 443–453.

Noton, D., & Stark, L. (1971). Scanpaths in eye movements during pattern perception., 308–311.

Pachur, T., Hertwig, R., Gigerenzer, G., & Brandstätter, E. (2013). Testing process predictions of models of risky choice: A quantitative model comparison approach., 646.

Pachur, T., Suter, R. S., & Hertwig, R. (2017). How the twain can meet: Prospect theory and models of heuristics in risky choice., 44–73.

Payne, J. W., & Braunstein, M. L. (1978). Risky choice: An examination of information acquisition behavior.(5), 554–561.

Polman, E. (2012). Self–other decision making and loss aversion.(2), 141–150.

Popovic, N. F., Pachur, T., & Gaissmaier, W. (2019). The gap between medical and monetary choices under risk persists in decisions for others.(4), 388–402.

Quiggin, J. (1982). A theory of anticipated utility.(4), 323–343.

Rao, L. L., Liu, X. N., Li, Q., Zhou, Y., Liang, Z. Y., Sun, H. Y., ... Li, S. (2013). Toward a mental arithmetic process in risky choices.(3), 307–314.

Rao, L. L., Zhou, Y., Xu, L., Liang, Z. Y., Jiang, T., & Li, S. (2011). Are risky choices actually guided by a compensatory process? New insights from fMRI.(3), e14756.

Rayner, K. (2009). Eye movements and attention in reading, scene perception, and visual search.(8), 1457–1506.

Savage, L. J. (1951). The theory of statistical decision.(253), 55–67.

Savage, L. J. (1954).. New York: Wiley.

Schmidt, U., Starmer, C., & Sugden, R. (2008). Third- generation prospect theory.(3), 203–223.

Su, Y., Rao, L. L., Sun, H. Y., Du, X. L., Li, X., & Li, S. (2013). Is making a risky choice based on a weighting and adding process? An eye-tracking investigation.(6), 1765–1780.

Sui, X. Y., Liu, H. Z., & Rao, L. L. (2020). The timing of gaze-contingent decision prompts influences risky choice., 104077.

Sun, H. Y., Rao, L. L., Zhou, K., & Li, S. (2014). Formulating an emergency plan based on expectation-maximization is one thing, but applying it to a single case is another.(7), 785–814.

Sun, H. Y., Su, Y., Zhou, K., & Li, S. (2011). From multiple-play to single-play in risky decision making: Quantitative change or qualitative change?(10), 1417–1425.

[孙红月, 苏寅, 周坤, 李纾. (2011). 从风险决策中的多次博弈到单次博弈：量变还是质变？(10), 1417–1425.]

Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty.(4), 297–323.

van der Stoep, S. W., & Seifert, C. M. (1994). Problem solving, transfer, and thinking. In P. R. Pintrich, D. R. Brown, & C. E. Weinstein (Eds.),(pp. 27–49). Hillstale, NJ: Erlbaum.

Velichkovsky, B. M., Rothert, A., Kopf, M., Dornhöfer, S. M., & Joos, M. (2002). Towards an express-diagnostics for level of processing and hazard perception.(2), 145–156.

Vinod, H. R. D., & Reagle, D. (2004).. Hoboken, NJ: Wiley.

von Neumann, J., & Morgenstern, O. (1947).. Princeton, NJ: Princeton University Press.

Wei, Z. H., & Li, X. Decision process tracing: Evidence from eye-movement data.(12), 2029–2041.

[魏子晗, 李兴珊. (2015). 决策过程的追踪: 基于眼动的证据.(12), 2029–2041.]

Zhang, Y. Y., Zhou, L., You, X., Li, S., & Liang, Z. Y. (2018). Is intertemporal decision-making based on a temporal discounting process? Evidence from double-dissociation paradigm.(5), 592–608.

[张阳阳, 周蕾, 游旭群, 李纾, 梁竹苑. (2018). 跨期决策是否基于“折扣计算”: 来自双分离范式的证据.(5), 592–608.]

Zhou, L., Zhang, Y. Y., Wang, Z. J., Rao, L. L., Wang, W., Li, S., ... Liang, Z. Y. (2016). A scanpath analysis of the risky decision-making process.(2–3), 169–182.

Zhou, Y. B., Li, Q., & Liu, H. Z. (2021). Visual attention and time preference reversals.(4), 1010–1038.

When expectation-maximization-based theories work or do not work: An eye-tracking study of the discrepancy between everyone and every one

LIU Hong-Zhi3, LI Xingshan1,2, LI Shu1,2,4, RAO Li-Lin1,2

(1CAS Key Laboratory of Behavioral Science, Institute of Psychology, Chinese Academy of Sciences, Beijing 100101, China) (2University of Chinese Academy of Sciences, Beijing 100049, China) (3Department of Social Psychology, Zhou Enlai School of Government, Nankai University, Tianjin 300350, China) (4Department of Psychology and Behavioral Sciences, Zhejiang University, Hangzhou 310028, China)

Mainstream theorists in risky decision-making have developed various expectation-maximization-based theories with the ambitious goal of capturing everyone’s choices. However, ample evidence has revealed that these theories could not capture every individual’s (“every one’s”) actual risky choice as descriptive theories. Substantial research has demonstrated that people do not follow the logical process suggested by expectation-maximization-based theories when making risky choices but rather rely on simplifying heuristics. From our perspective, the possible reason why mainstream decision theorists did not abandon the framework of expectation is that these theorists never doubted the validity of the expectation rule as a descriptive rule in describing decision-making under risk. We believe that expectation-maximization-based theories may capture risky choices when individuals make decisions for everyone. However, whether these theories could capture risky choices when individuals make decisions for themselves cannot be taken for granted. We thus used an eye-tracking technique to explore whether a theory for everyone would work well for every one.

A total of 52 college students participated in the experiment. Three risky choice tasks were conducted in the present study: a D-everyone task, a D-multiple task, and a D-single task. In the D-everyone task, participants were asked to choose the more optimal option out of two options under the assumption that their selection would be the final decision for everyone who was facing the same choice—that is, everyone would be subject to the same choice but could receive different outcomes. In the D-multiple task, participants were asked to choose between the two options under the assumption that their selection would be applied a total of 100 times. In the D-single task, participants were asked to choose between the two options under the assumption that their selection would be applied only once to themselves. The participants’ eye movements were recorded while they performed the tasks.

Behavioral results revealed that, compared with the D-single task, participants selected more choices correctly predicted by EV and EU theories, and took a longer time to make a decision in the D-everyone and D-multiple tasks. Furthermore, eye movement measurements revealed the following. (1) The scanpath patterns of the D-everyone task and D-multiple task were similar but different from those of the D-single task. (2) The depth of information acquisition and the level of complexity of information processing in the D-everyone task and D-multiple task was higher than that in the D-single task. (3) The direction of information search in the D-everyone task and D-multiple task was more alternative-based than that in the D-single task. (4) The eye-tracking measures mediated the relationship between the task and the EV-consistent choice. In summary, behavioral and eye movement results supported our hypotheses that participants were likely to follow an expectation strategy in the D-everyone and D-multiple tasks, whereas they were likely to follow a heuristic/non- expectation strategy in the D-single task.

We found that expectation-maximization-based theories could capture the choice of an individual when making decisions for everyone and for self in a multiple-play condition but could not capture the choice of an individual when making decisions for self in a single-play condition. The evidence for the discrepancy between everyone and every one, which was first reported in our study, implied that the possible reason why expectation-maximization-based theories do not work is that a default compatibility between the full set (everyone) and the subset (every one) does not exist. Our findings contribute to an improved understanding of the boundaries of expectation-maximization-based theories and those of heuristic/non-expectation models. Our findings may also shed light on the general issue of the classification of risky decision-making theories.

risky choice, decision for everyone, expectation-maximization, discrepancy between everyone and every one, eye-tracking

2022-01-22

* 国家自然科学基金项目(71901126), 国家社会科学基金重大项目(19ZDA358), 教育部人文社会科学研究青年项目(19YJC190013)和中央高校基本科研业务费专项资金(63222045)资助。

饶俪琳, E-mail: raoll@psych.ac.cn

B849: C91