均匀流场中钢管桩基础水动力时域统计特性

张显雄

（保利长大工程有限公司，广东 广州 510620）

圆柱形钢管桩基础是海洋结构工程普遍采用的一种水下支撑形式，在海上风电项目方面的应用尤为广泛。圆柱的水动力特性是一个极为复杂的课题，作为海洋结构的下部支撑时，其在流动力环境中的性能直接影响上部结构的安全。

以海上风电项目为例，我国对海上风机的设计主要参考现行行业标准《海上固定平台规划、设计、建造推荐作法- 工作应力设计法》(SY/T 10030-2018)，其波浪荷载是根据Morison 方程计算的一种以表层流作用为主的等效静力荷载。在远岸海域以及陡峭大陆架海域，相对表层波浪更稳定的深层均匀流有可能使风机的下部圆柱支撑发生周期性的涡激共振。根据Morison 方程得到的等效静力荷载不足以描述这种深层均匀流对风机下部支撑的真实动力作用。而且，我国现行的《海上固定平台规划、设计、建造推荐作法－工作应力设计法》(SY/T 10030-2018)对深层均匀流荷载的动力作用没有明确规定。

目前，在我国南海海域风电项目的单圆柱桩基直径D 高达9 m，绕流场的Re 数高达107量级，属于超高Re数，无论是试验还是数值模拟，将对研究条件提出十分苛刻的要求，常用的方法是取其缩尺模型进行分析。虽然缩尺会使圆柱的流场Re 数区间发生明显偏离，但如果缩尺后的流场能够同时出现边界层转捩、剪切层分离、回流等复杂流动流动现象，则认为缩尺模型的研究结果在很大程度上可以代表真实流动情形。文献[2]与文献[3]的研究结果表明，当Re 数为3 900 时，圆柱流场依然体现出边界层转捩、剪切层分离、回流等复杂流动流动现象。因此本文模拟均匀流场中单圆柱桩基的荷载特性时，其Re 数为3 900。

1 研究方法

1.1 基本理论 Nicoud 等人[1]建立WALE 亚格子模型时，在笛卡尔坐标系中将涡黏系数μt表示为：

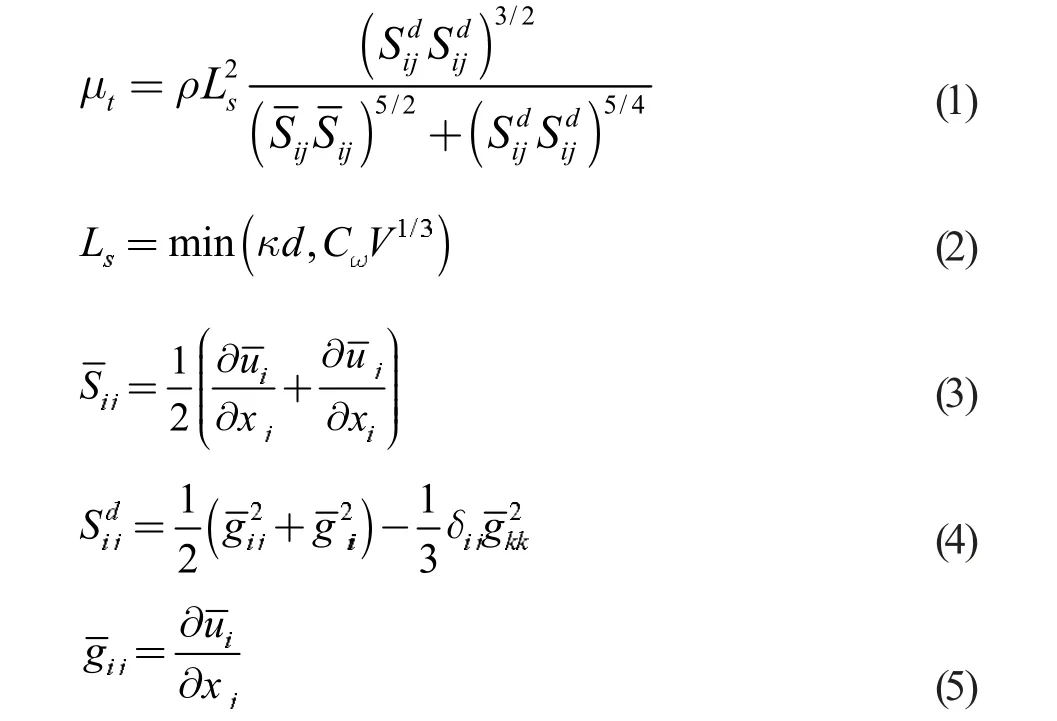
式中各项参数的意义具体详见文献[1]。

1.2 缩尺模型计算域 单圆柱桩基绕流场平均速度U的剖面见图1。在沿海面一定距离的深度内，流平均速度的变化较小，可以近似认为是均匀来流。因此，在这一深度范围截取一定长度的桩基进行分析，可以获得具有代表性的均匀流作用在圆柱桩基上的荷载。

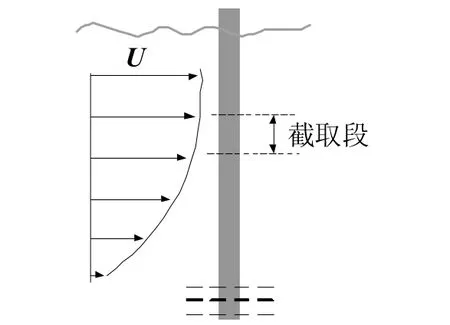
图1 圆柱形桩基截取段示意图

与Lehmkuhl 等人[2]的直接数值模拟(Direct Numerical Simulation, DNS)计算域相同，模型缩尺以后，在来流的X 方向，圆柱前场计算域长度为8 D，尾流场计算长度为16 D；在横流Y 方向，计算域设置为对称形式，宽度为20 D；二维流场沿Z 方向扩展πD 形成三维流场。流场的计算域具体布置形式见图2。

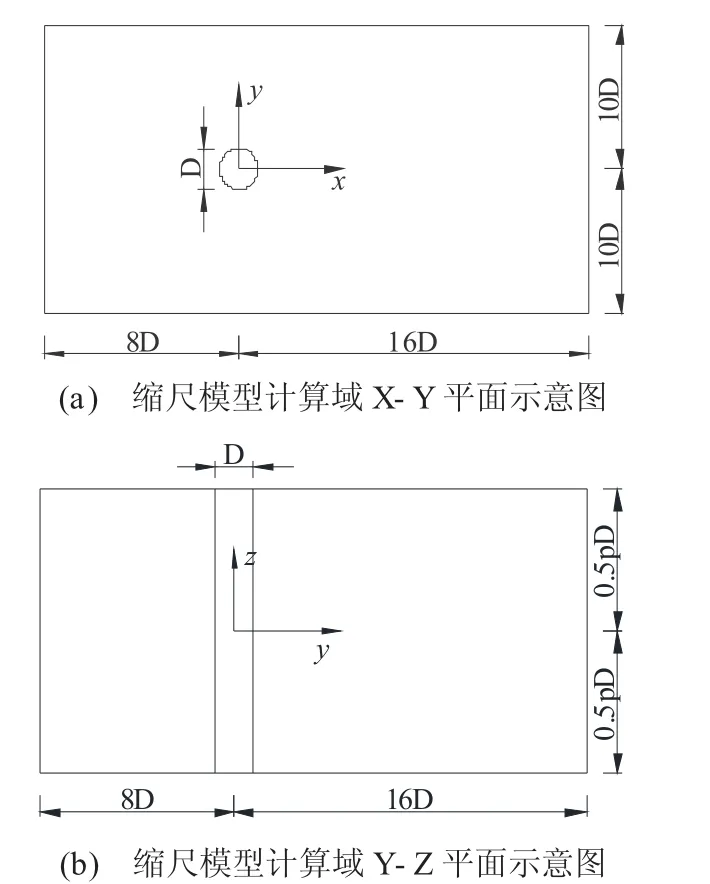
图2 圆柱形桩基缩尺模型计算域详细尺寸

来流边界条件为速度来流，X 方向来流速度U 为均匀来流；出口边界为压强条件；圆柱表面为固壁无滑移条件；计算域其余界面为对称边界条件。取20 ℃时的海水密度ρ 为998.2 kg/m3；海水的动力黏性系数μ 取1.008 18×10-3Pa·s。缩尺后后流场Re 数为3 900。参照文献[3]与文献[4]的计算方法，计算域采用结构化网格进行离散；圆柱近壁面网格的Yplus 值控制在1 以内。经过无关性检验后，最终的网格数量为3 792 375，无量纲时间步长Δt×U/D=0.025。Navier-Stokes 方程组的瞬态项迭代采用二阶隐式向后前差分法；空间离散采用二阶中央差分法；速度压强解耦采用Vandoormaal 等人提出的SIMPLE-C算法[5]。本文统计的压强时程超过326 个涡脱周期。

2 数值结果合理性验证

Lehmkuhl 等人[2]采用DNS计算了相同Re 数条件下三维圆柱绕流场在涡生成区域内的低频不稳定特性，并给出了流场部分一阶统计量的高精度结果。本文将计算得到的圆周压强时程P(ti)的一阶结果与Lehmkuhl 等人的DNS结果相对比，从而判断本文模拟的合理性。

定义圆周表面无量纲水压系数时程为式(6)：

定义圆周表面无量纲时间平均(Time-Averaged)的水压系数为式(7)：

定义单位长度圆柱的无量纲阻力系数为式(8)：

定义圆柱流场的无量纲涡脱频率为式(9)：

整体水动量模拟结果见表1。

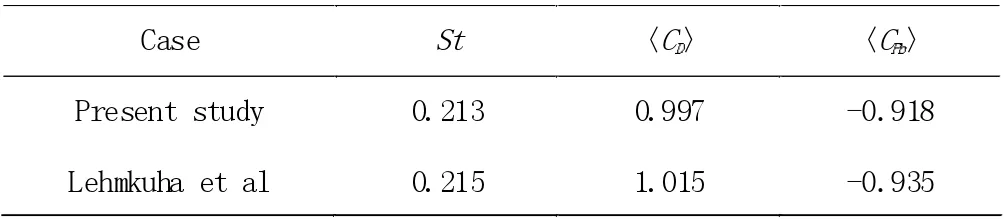
表1 圆周水压的整体模拟结果

从表1 的整体水动量模拟结果可以看出：对于无量纲涡脱频率St，本文的模拟结果与Lehmkuhl 等人的DNS 结果的相对偏差仅为0.93%；对于平均阻力系数〈CD〉，本文的模拟结果与Lehmkuhl 等人的DNS 结果的相对偏差仅为1.78%；对于平均基压系数〈CPb〉，本文的模拟结果与Lehmkuhl 等人的DNS 结果的相对偏差仅为1.81%。整体而言，本文的模拟结果具有相当高的精度。

图3 对比了本文模拟的圆周平均水压系数结果与Lehmkuhl 等人的DNS 结果。从水压系数的一阶统计量沿圆周表面的分布来看，本文的LES 模拟结果与Lehmkuhl 等人的DNS结果吻合较好。最大偏差出现在θ≈±72°位置处，本文的LES 模拟结果与Lehmkuhl 等人的DNS结果的相对偏差为1.16%。

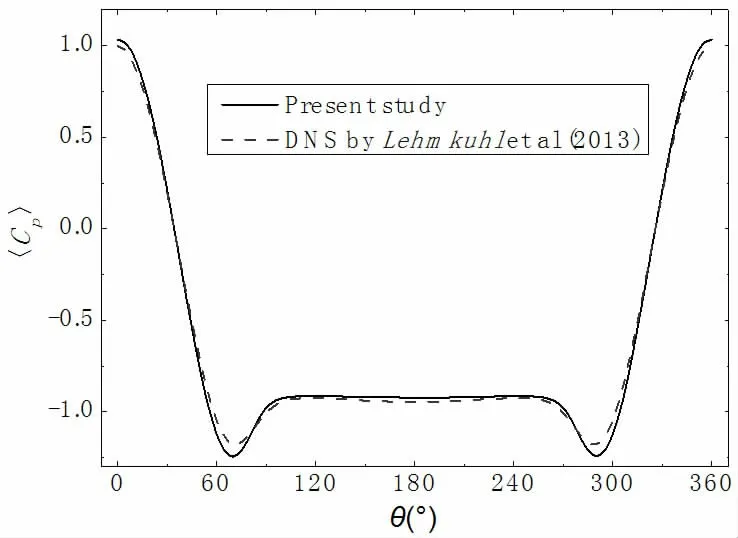
图3 圆周平均水压系数模拟结果

因此，不论是从整体水动量模拟结果来是从水压系数的一阶统计量沿圆周表面的分布的结果来看，本文的模拟具有相当高的精度，其结论可靠，可以用于指导工程应用。

3 数值结果的时域统计特性

3.1 相关性 定义圆周水压系数与驻点（θ0=0°）水压的相关系数为式(10):

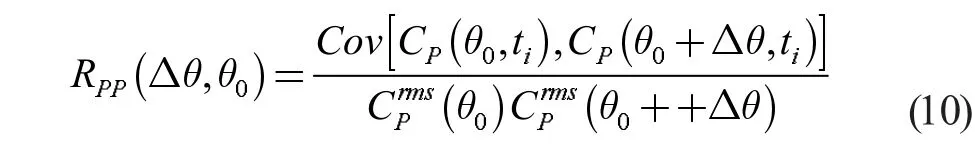
图4 列出了本文模拟圆周水压相对驻点水压的相关系数分布结果。曲线以Δθ=180°为对称轴呈对称分布，符合均匀流场中圆柱表面水压的分布特征，进一步认证了本文模拟结果的精度。从驻点位置(Δθ=0°)开始，圆柱表面水压相关性急速降低，至Δθ≈35°时，圆柱表面水压相关性为零，表明此处流动已经完全呈现出非线性特征。与此相对应的是图3 所列的圆周平均水压系数分布情况，在此处平均水压系数由正转负，表明流动可能出现回流。

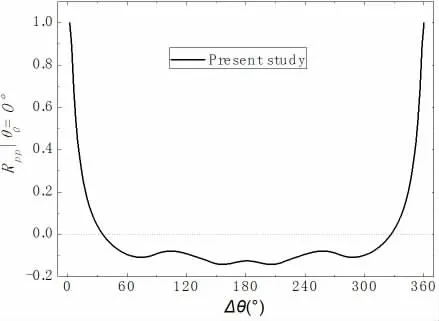
图4 圆周水压的相关系数分布

在Δθ≈35°～Δθ≈325°的区间内，圆柱表面水压相对驻点水压的相关性为负，但相关性较低，不足0.2，与此相对应的是图3 所列的圆周平均水压系数为负值。这一现象表明在此区间内，流动虽然仍然具有一定的线性特征，但流场的非线性因素起控制作用。

3.2 二阶统计特性 定义圆周流场水压的二阶时域统计量，即脉动标准差(Standard Deviation)，为式(11):

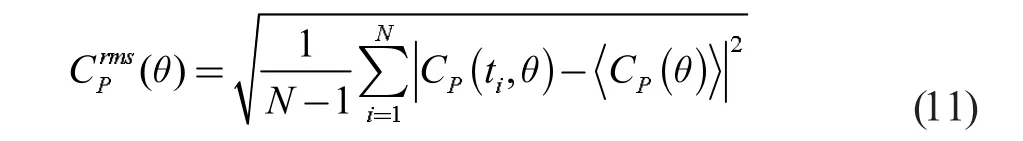
图5 所示本文模拟的圆周水压时程脉动标准差沿圆周分布与Norberg的试验结果[6]具有相同的趋势，但Norberg 的试验结果偏大，这是因为Norberg 在根据式(11)处理试验结果时考虑了时间平均水压系数。

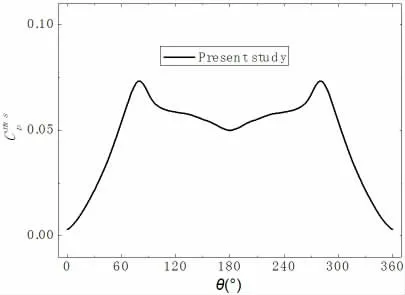
图5 圆周水压时程的脉动标准差

从图5 所示的本文模拟结果分布可知，其峰值出现在θ≈±80°位置处，而本文模拟的流动分离点在θ≈±87.1°位置处，与Lehmkuhl 等人的DNS结果θ≈±88°位置极为接近，表明流动分离点与圆周水压脉动峰值位置并没有直接关系。

另外，圆周水压的脉动最大值与圆周平均水压的最小值并不出现在相同位置，而且水压的脉动最大值出现在相关系数为负的区间。二阶时域统计量进一步说明了圆周流场的非线性程度。

3.3 三阶统计特性 定义圆周流场水压的三阶时域统计量，即偏斜度(Skewness)，为式(12):

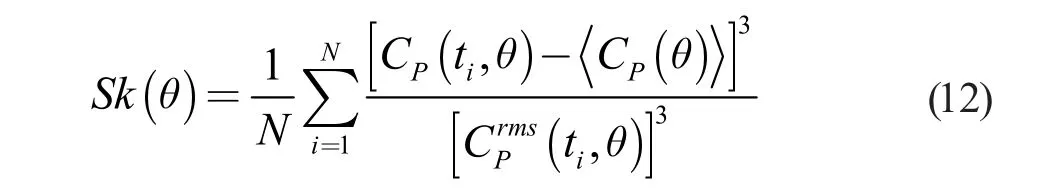
从图6 所示的圆周流场水压的偏斜度分布曲线可知，圆周水压在绝大部分范围内均为负值，即左偏分布，表明圆周表面的水压时程并非呈高斯分布，而是大量较高的水压时程值密集分布在平均值的右边。从圆周驻点位置(θ＝0°)开始至θ≈±134°位置处，流场水压的左偏程度越来越明显；而从θ≈±134°位置开始至圆周基压点位置(θ＝180°)，流场水压的左偏程度有所减轻。这一现象说明圆柱在均匀来流条件下，不论边界层内流动是否出现转捩现象，圆柱的存在都将影响周边流场的脉动。虽然对这一影响的解释目前没有形成共识，但圆周水压时程偏斜度分布特征表明圆柱周边各部位的脉动流场内必然隐含着相似的流动机理。

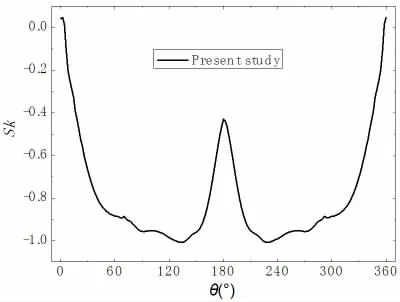
图6 圆周水压时程的偏斜度

3.4 四阶统计特性 定义圆周流场水压的四阶时域统计量，即陡峭度(Kurtosis)，为式(13):

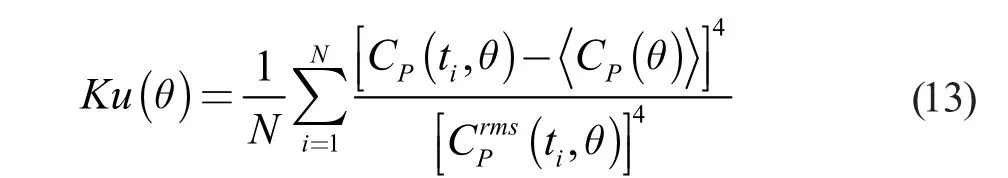
从图7 所示的圆周流场水压的峰度分布曲线可知，圆周水压在绝大部分范围内均大于3，即为平缓分布，表明圆周表面水压时程的概率密度在平均值处局限在一定范围内，不会出现突变。在均匀流作用下，从圆周驻点位置(θ＝0°)开始至本文模拟的流动分离点位置θ≈±87.1°位置处，流场水压的水压时程脉动量峰度越来越大；在分离点之后的一小段范围内(约16°范围)，峰度值分布较为平稳；之后峰值度继续增大，至在θ≈±154°的位置峰度呈最大值。

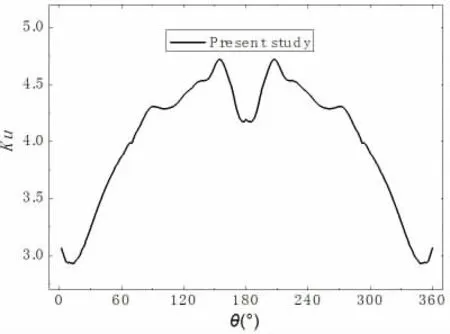
图7 圆周水压时程的峰度

从本文模拟圆周表面水压的二阶、三阶、四阶统计量分布特征综合来看，在圆周基压点位置(θ＝180°)附近一段范围内，各阶统计量均呈现出与其它圆周范围内不相同的分布规律。由于在圆周基压点附近，该Re 数所对应的流场已经发展成为高度湍流状态。因此一种可能的解释是，随着湍流程度的发展，流场的平均值虽然不会受影响，但脉动值随机特征的将发生显著变化。

3.5 峰值因子 峰值因子（Peak factor，Pf）可以在钝体绕流工程研究中用来确定设计水压或水压系数。在早期，Davenport[7]假定钝体绕流场的脉动量服从高斯分布(Gaussian distribution)，基于零值穿越率理论建立了传统峰值因子的计算方法。但是现有研究表明钝体绕流场的脉动量并非呈高斯分布，传统峰值因子的计算结果偏小，不利于工程应用。

本文根据LES模拟结果，将圆周表面的非高斯水压时程通过Hermite 多项式转换为高斯分析，从而计算出考虑了非高斯性质的圆周水压峰值因子，并对比了Davenport 的传统计算方法与Hermite 多项式计算方法的差异见图8，对于研究圆柱桩基的流荷载具有重要的工程意义。高斯因子的Hermite 多项式计算方法详见文献[8]。

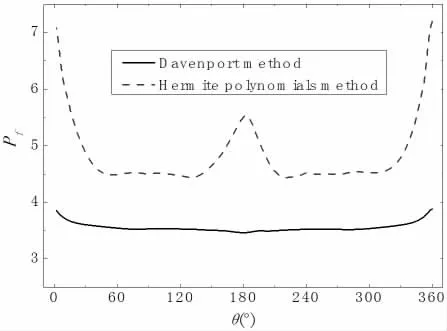
图8 圆周水压峰值因子分布

从图8 可知，Davenport 传统方法计算的圆周水压峰值因子明显低于Hermite 多项式的计算结果，而且Davenport 的计算结果沿圆周分布较为均匀，在平均值3.55 左右发生微幅波动。Hermite 多项式的计算结果沿圆周大概可以分为三个区间，即θ=0°～θ≈±46°，在此区间内峰值因子急剧降低；θ≈±46°～θ≈±136°，此区间内的峰值因子分布平缓；θ≈±136°～θ≈±180°，在此区间内峰值因子迅速增大，但在圆周基压位置处的峰值因子依然没有恢复至圆周驻点位置处的最大值。

4 结论

本文采用WALE 亚格子模型对Re=3 900 的单圆柱桩基流绕流场缩尺模型进行了大涡数值模拟，得到了以下几点结论：(1) 在本文模拟的Re 数条件下，来流为均匀流时，圆周水压的各阶统计量呈对称分布。(2) 圆周负水压区范围内水压时程的线性相关程度较低，其附近流域的非线性因素对流场起控制作用。(3) 圆周水压各阶统计量的峰值不出现在同一位置，表明各阶统计量分别对应不同的圆周绕流场流动特征。(4) 考虑水压分布的非线性效应时，均匀流作用下的圆周水压峰值因子偏大，且其沿圆周呈现出三个分布区间。