城市轨道交通轨道不平顺对振动源强环境影响评价研究

岳思

中铁第四勘察设计院集团有限公司

截至2021 年底，全国共有50 个城市开通城市轨道交通运营线路283 条，运营线路总长度9 206.8 km[1]（本文中的全国数据未包含港澳台）。城市轨道交通作为主要的城市公共交通系统之一，给人们日常生活带来极大便利的同时，引起的噪声振动影响也日益明显[2-7]。在城市轨道交通运营线路中有地下线、高架线、地面线等几种形式，其中地下线约占总线路长度的70%[8]。因此，轨道交通穿越城区时列车引发的周边环境振动问题逐渐变得越来越突出。

2017 年，全国已通车的轨道交通线路（不含有轨电车、单轨等）最高设计速度为60～120 km/h（不含上海高速磁浮线），其中设计时速100 km/h 以上的线路仅占18.8%。2018—2020年，国家发展和改革委员会相继批复了长春、苏州、重庆、上海、武汉等14 个城市的轨道交通建设规划（及规划调整），共涉及94 条规划线路，其中设计时速100 km/h 以上的线路占45.7%，较之前有了大幅提高。

2018 年10 月9 日，生态环境部发布了HJ 453—2018《环境影响评价技术导则 城市轨道交通》。与HJ 453—2008 相比，HJ 453—2018 在振动源强测试及预测等方面做了大幅修改。HJ 453—2008 规定，地下线路振动源强的测试位置为道床上部近轨外侧0.5～1.0 m 处；而HJ 453—2018 规定，地下线路振动源强的测试位置为隧道壁上高于轨面（1.25±0.25）m处。同时，HJ 453—2018 给出了列车速度小于等于100 km/h 的速度修正系数（CV），并指出当列车运行速度大于100 km/h 时，该公式不能直接使用，CV需要通过类比测量或符合工程实践的研究成果得到[9]。此外，轨道不平顺是车辆-轨道耦合系统的直接激励源，有必要分析不平顺程度的振动源强随着列车运行速度提高而受到的影响。

因此，为适应城市轨道交通设计时速不断提高的趋势，并为设计时速100～120 km/h、不同轨道不平顺谱条件下的振动环境影响评价及减振设计提供参考依据，开展城市轨道交通轨道不平顺对振动源强环境影响评价研究具有很强的必要性。

1 研究方法

为分析HJ 453—2018 给出的振动速度修正半经验公式的适用性，在与现场实测结果对比验证的基础上，计算分析列车运行速度、轨道不平顺条件对环境振动源强时频域特性的影响。具体内容包括：1）振动源强实测数据分析及模型验证。对实测数据进行时频域分析，统计振动源强的基本特征，并对本次的仿真模型及方法进行验证；将同一断面不同运行速度列车引发的环境振动最大Z 振级（VLZmax）与HJ 453—2018 提供的半经验公式进行对照分析。2）振动速度修正半经验公式预测参数优化。优化在不同运营条件下CV的半经验公式，并考虑轨道不平顺的影响，通过数值仿真计算出时速为100～120 km/h 的速度修正系数，给出最终建议值。

1.1 现场测试断面设置情况

选取设计时速为100 km/h 的断面1 和2 进行测试，分析不同速度条件下的基底和隧道壁的振动加速度主频分布规律。为分析轨道交通线路提速运行下，HJ 453—2018 给出的振动预测CV公式的适用性，选取设计时速为120 km/h 的断面3 作为对比验证。

1.2 振动预测仿真模型建立及验证

在对环境振动影响进行预测的过程中，采用车辆-轨道空间耦合动力学模型和轨道-隧道-土体三维有限元-无限元耦合模型进行仿真，主要步骤如下。

第一步：在车辆-轨道耦合动力学模型中输入轨道不平顺激励进行耦合系统动力响应求解，并提取编组列车运行过程中轨道纵向扣件系统支反力的时程曲线。

第二步：将提取的扣件力时程曲线作为激励输入到三维有限元-无限元隧道-地层模型中，采用隐式动力算法进行求解，提取隧道壁上位于轨面以上1.25 m 位置处节点加速度作为环境振动源强评价量。

第三步：用断面实测数据对建立的车辆-轨道空间耦合动力学模型和三维有限元-无限元耦合模型进行验证。

（1）车辆-轨道耦合动力学模型

根据隧道断面测试列车及轨道参数，在Matlab软件中通过编程建立了编组列车-轨道耦合动力学模型[10-12]（图1）。

图1 车辆-轨道耦合动力学模型示意Fig.1 Schematic diagram of vehicle-track coupled dynamics model

（2）隧道-地层有限元-无限元耦合模型

隧道-地层有限元-无限元耦合模型如图2 所示，模型沿线路总线延伸120 m，垂直于线路中心宽度为70 m，土层深度为80 m。对隧道和土层进行建模分析时，模型右侧采用无限单元边界，模型左侧采用对称边界，模型上侧的地面土体为自由边界，模型底部采用固定边界[13]。有限元模型的求解频率上限与网格尺寸相关，网格划分尺寸太小会导致计算频率上限过低，但网格尺寸过小会导致计算中单元数量过多，增加计算成本。因此，为提高计算效率同时保证计算精度，在对模型进行网格划分时，隧道结构的网格尺寸选择为0.025 m，非无限单元区域土体的网格尺寸选择为0.1～1 m，无限单元区域土体不考虑网格尺寸，采用这种尺寸进行网格划分可以满足环境振动分析频率上限的200 Hz 要求[14-17]。

图2 有限元-无限元三维仿真模型Fig.2 Finite element-infinite element three-dimensional simulation model

2 结果与讨论

2.1 振动源强断面实测数据时频域分析

2.1.1 断面1 实测数据时频域分析

断面1 为某市轨道交通2 号线，设计时速为100 km/h，6 节编组B 型车，直线段，坡度12.8‰，轨道埋深18 m。根据200 Hz 以内基底加速度和隧道壁加速度的主频分布测试结果，在70 辆检测列车中，有33 辆主频位于中心频率为100 Hz 的频带内，32 辆位于中心频率为80 Hz 的频带内，占比分别为47.1%和45.7%。对于隧道壁加速度，70 辆编组列车中有57 辆的加速度主频位于中心频率为80 Hz 的频带内，占比为81.4%。其中，列车33、34 和35 基底加速度1/3 倍频程谱的主频分别位于中心频率为80、100和125 Hz 的频带内，列车29、30、31 隧道壁加速度1/3 倍频程谱的主频分别位于中心频率为63、80 和100 Hz 的频带内，相邻频带的能量相差不大。

由图3 可知，随着列车运行速度的提高，基底加速度的主频向更高频带移动，振级随之提高。此外，基底和隧道壁上的振动加速度频谱在低频也呈现出明显的增幅趋势，这是由于列车运行速度的提高，列车受到相同频率的激振源逐渐向长波方向移动，由于轨道不平顺呈现明显的对数特性，使得低频部分的激振能量会明显提高。

图3 断面1 不同运行速度列车引起基底和隧道壁振动加速度1/3 倍频程谱均值Fig.3 Mean value of 1/3 octave frequency spectrum of vibration acceleration of base and tunnel wall caused by trains with different operating speeds in section 1

2.1.2 断面2 实测数据时频域分析

断面2 为某市轨道交通1 号线，设计时速为100 km/h，6 节编组B 型车，直线段，坡度3‰，轨道埋深27 m。测试结果显示，断面2 的基底和隧道壁的振动加速度主频分别位于中心频率为80 和63 Hz 的频带内，与断面1 相似。

图4 给出了2 种运行速度下列车引起的振动加速度1/3 倍频程谱均值曲线，可以观察到由于轮轨一阶共振加剧，列车运行速度提升后主频向63 Hz 为中心频率的频带移动，该频带内的分频振级显著增加。

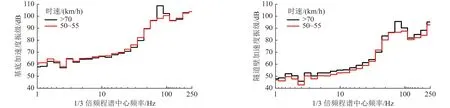
图4 断面2 不同运行速度列车引起基底和隧道壁振动加速度1/3 倍频程谱均值Fig.4 Mean value of 1/3 octave frequency spectrum of vibration acceleration of base and tunnel wall caused by trains with different operating speeds in section 2

2.1.3 断面3 实测数据时频域分析

断面3 为某市轨道交通16 号线，设计时速为120 km/h，6 节编组A 型车，直线段，坡度2‰，轨道埋深21 m。由测试结果可知，同一断面不同列车引起的隧道壁振动加速度1/3 倍频程谱，振动加速度主频亦位于中心频率为63 Hz 的频带内。挑选出现频率大于10 的数据求平均值，其中104～105 km/h 出现频率为15，105～106 km/h 出现频率为53，远超出其他速度出现频率，置信度较高，因此对68 组速度为104～106 km/h 源强数据开展分析后可得出，速度105.2 km/h 时振动源强Z 振级为82.4 dB。

2.2 振动源强时频域预测结果验证分析

2.2.1 设计时速100 km/h 实测断面预测模型验证分析

通过车辆-轨道空间耦合模型计算得到的扣件力被作为模型输入到三维有限元模型上，随后通过隐式动力方法进行时域求解。隐式动力积分步长决定了模型的分析频率上限，减小积分步长可以得到更宽频域范围内的计算结果，但是会大大提升计算成本。对于环境振动研究，通常关心的频率范围为1～80 或1～200 Hz，因此选择积分步长为0.001 s，对200 Hz 以内的振动响应求解可以认为具有足够的精度[18]。

从图5 可知，三维模型仿真振动源强时域预测与实测结果的振动加速度幅值校对良好，实测结果在列车经过测试位置时表现出一些较为尖锐的“毛刺”，可能由于钢轨表面伤损或车轮扁疤引起。这些信号的频率通常在400 Hz 左右，而环境振动预测通常只关注200 Hz 以下的振动响应，因此可认为采用的仿真模型是合适的。

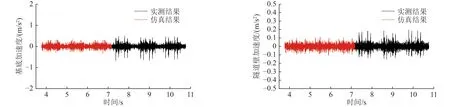
图5 振动实测与有限元-无限元三维模型仿真源强时域预测结果Fig.5 Measured vibration and simulated source intensity time domain prediction results of finite element-infinite element three-dimensional model

由图6 可以看出，对于200 Hz 以下的隧道壁源强振动加速度信号，各频带内的振级均在实测结果的包络线范围之内，仿真模型计算结果与实测结果吻合良好。因此可认为建立的车辆-轨道三维耦合动力学模型和有限元-无限元三维模型在环境振动源强仿真的过程中具有足够的精度。

图6 测试断面1 隧道壁和基底振动加速度1/3 倍频程谱对比Fig.6 Comparison of 1/3 octave frequency spectrum of vibration acceleration of the tunnel wall and the base of the test section 1

2.2.2 设计时速120 km/h 实测断面预测模型验证分析

为验证采用的数值方法在较高运行速度条件下的适用性，给设计时速为120 km/h 的轨道交通16 号线环境振动源强建立了有限元模型进行数值仿真比较。图7 为隧道壁上的振动加速度信号时域和1/3 倍频程谱结果。由图7 可看出，仿真结果和实测结果整体趋势一致，在主频处的分频振级分别为88.4、88.1 dB，最大Z 振级分别为82.02、82.4 dB，数值仿真计算得到的振动信号与实测值的最大Z 振级较为接近。综上，可以认为采用的环境振动数值仿真模型可以在较高列车运行速度条件下能取得足够的预测精度。

图7 隧道壁上的振动加速度信号时域和1/3 倍频程谱结果对比Fig.7 Comparison of vibration acceleration signal in time domain and 1/3 octave spectrum on tunnel wall

2.3 轨道不平顺振动环境影响预测模型CV 应用分析

由于轨道不平顺是车辆-轨道耦合系统振动环境影响的直接激励源，其频域幅值分布特性将会决定环境振动源强的时频特性，有必要分析不平顺裂化程度不同的线路上环境振动源强随着列车运行速度提高而受到的影响。因此，选用3 种不同的轨道不平顺作为激励，分别为美国五级谱+中国铁道科学研究院（简称铁科院）短波不平顺谱、美国五级谱+ISO 粗糙度谱和美国五级谱，其中美国五级谱为长波不平顺，其波长大于1 m，铁科院短波不平顺和ISO粗糙度谱均为短波谱，其波长小于1 m，这3 种谱线的恶劣程度从差到好排序为美国五级谱+铁科院短波不平顺谱、美国五级谱+ISO 粗糙度谱和美国五级谱[19]。首先仿真分析列车提速过程中最大Z 振级的变化情况，进而分析HJ 453—2018 给出的CV在轨道不平顺恶劣状态不同的线路上振动环境影响评价的适用性。

由图8～图10 给出的编组列车在3 种轨道不平顺激励下隧道壁振动加速度随着列车运行速度提高发生的变化情况可知，与输入不平顺激励的PSD 谱线高低相对应的，在短波部分铁科院短波不平顺谱提供的能量最多，ISO 粗糙度谱其次，而采用美国五级谱函数关系式直接得到的谱线能量最低。不同轨道不平顺激励条件下列车运行速度与最大Z 振级详见表1。

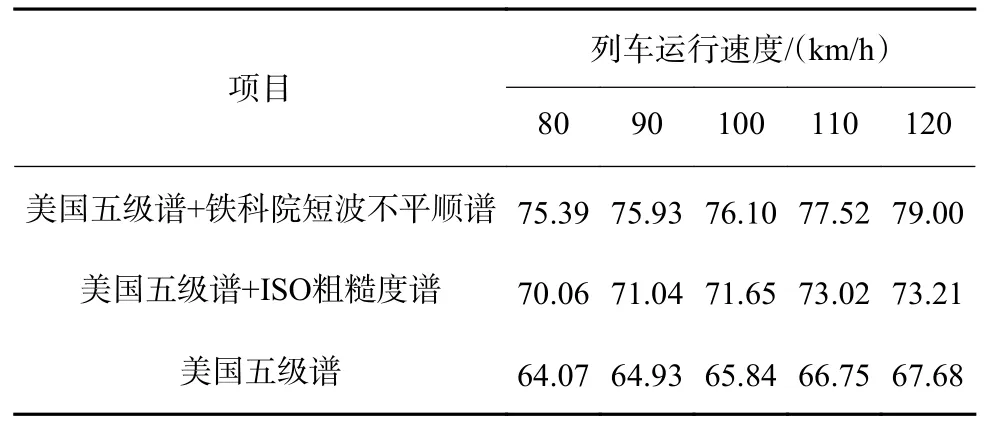
表1 不同轨道不平顺激励条件下速度与最大Z 振级Table 1 Velocity and maximum Z vibration level under different orbital irregularity excitation conditions dB

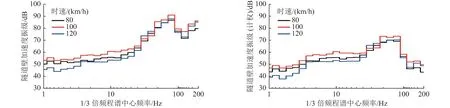
图8 隧道壁振动源强1/3 倍频程谱（美国五级谱+铁科院短波谱）Fig.8 1/3 octave frequency spectrum of vibration source intensity of tunnel wall (U.S.fifth-order spectrum+short-wave spectrum of Academy of Iron Sciences)

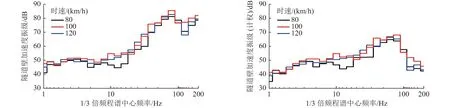
图9 隧道壁振动源强1/3 倍频程谱（美国五级谱+ISO 粗糙度谱）Fig.9 1/3 octave frequency spectrum of tunnel wall vibration source intensity(U.S.fifth-order spectrum+ISO roughness spectrum)

图10 隧道壁振动源强1/3 倍频程谱（美国五级谱）Fig.10 1/3 octave frequency spectrum of tunnel wall vibration source intensity (U.S.fifth-order spectrum)

对于速度小于100 km/h 的城市轨道交通线路，HJ 453—2018 给出的CV计算公式为：

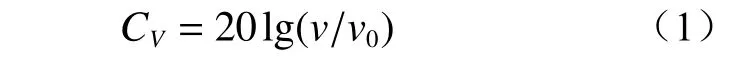
根据HJ 453—2018 给定的速度修正规则，用于作为修正基准的速度（ν0）需至少为预测运行速度（v）的75%。因此在进行CV比对时，时速为90 和100 km/h 的选择时速80 km/h 的计算结果为基准速度；时速为110 和120 km/h 的选择时速100 km/h 的计算结果为基准速度。

由表2 可知，当列车运行速度小于等于100 km/h 时，仿真结果得到的CV都小于HJ 453—2018的给定值（20），意味着HJ 453—2018 给出的公式偏保守；当列车运行速度超过100 km/h，仿真结果得到的CV普遍大于20。

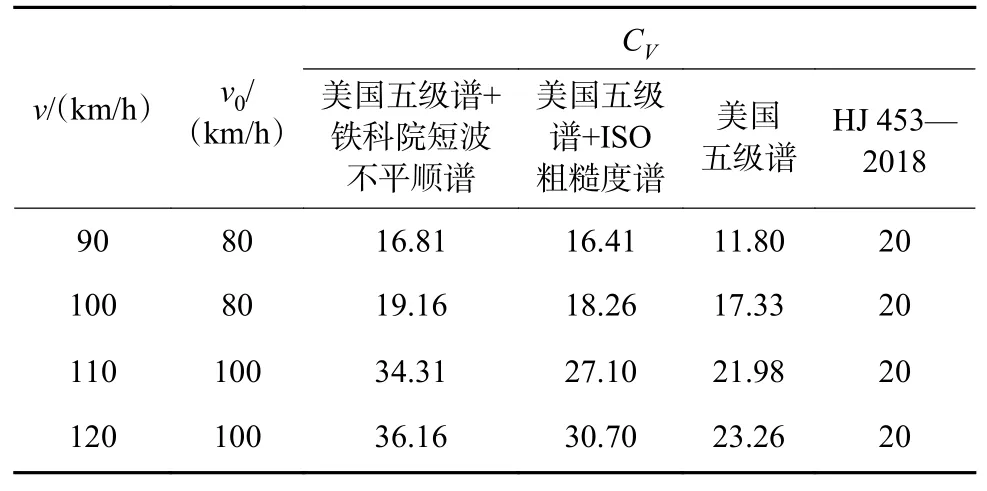
表2 以不同速度为基准的速度修正系数Table 2 Speed correction coefficients based on different speeds

从以上计算结果可知：1）当列车运行速度小于等于100 km/h 时，HJ 453—2018 给定的振动速度修正项CV与美国五级谱+ISO 粗糙度谱和美国五级谱激励下仿真计算得到的结果较为接近，且对3 种不平顺激励下的结果来说都偏保守，因此HJ 453—2018在列车运行速度100 km/h 及以下对轨道不平顺不同恶劣程度的线路振动环境影响评价具有较好的适用性；2）当列车运行速度大于100 km/h 时，地铁编组列车运行引发的环境振动源强呈现更加剧烈的增幅趋势，此时，通过HJ 453—2018 公式得到的CV普遍小于仿真结果，100 km/h以下的速度修正系数已不再适用。

为了在地铁列车提速之后振动环境影响评价结果偏于保守，建议将列车运行速度为100～120 km/h、不同轨道不平顺谱条件下的速度修正如下：

当轨道条件恶劣（采用美国五级谱+铁科院短波不平顺谱）时：

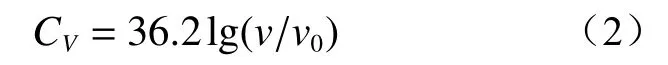
当轨道条件一般（采用美国五级谱+ISO 粗糙度谱）时：

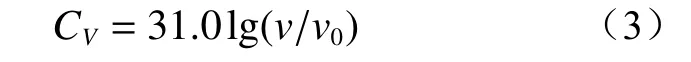
当轨道条件较好（采用美国五级谱）时：

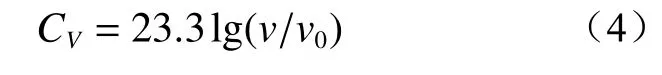
3 结论

（1）当城市轨道交通运行速度位于100 km/h 及以下时，HJ 453—2018 给出的振动环境影响速度修正系数20 是适合的。

（2）当城市轨道交通运行速度位于100～120 km/h、不同轨道不平顺谱条件下，建议振动环境影响速度修正为：当轨道条件恶劣（采用美国五级谱+铁科院短波不平顺谱）时，速度修正系数建议值为36.2；当轨道条件一般（采用美国五级谱+ISO 粗糙度谱）时，将速度修正系数建议值为31.0；当轨道条件较好（采用美国五级谱）时，将速度修正系数建议值为23.3。