基于模糊PID的轨道式巡检机器人步进电机控制算法
2022-12-05丛峰武高太李熙然刘皓月
丛峰武 高太 李熙然 刘皓月
1.鞍山钢铁集团有限公司齐大山选矿厂;2.大连交通大学
本文为实现巡检机器人控制系统响应速度快、超调量小、遇到电压和负载波动突变的情况下能够自动调节的需求,设计了模糊PID 控制器,通过建立模糊规则,采用Mamdani 法进行推理,实现参数在线调整。将传统PID 算法、BP-PID 控制算法与本文所设计的模糊PID控制算法进行对比。根据仿真结果,模糊PID 控制器系统响应速度最快,精度最高,因此可应用于巡检机器人步进电机控制。
我国是煤炭能源大国,在煤炭运输的多个环节都有着带式输送机的身影,在煤炭物料运输的过程中需要对输送机状态进行监控。但是由于选矿厂工作环境十分恶劣,不能满足人们的正常工作环境。因此在铁矿等重要危险区域采用智能巡检机器人代替人工巡检,减少人员投入,保障巡检有效执行[1]。巡检机器人的机械结构是由五个轮组成,其中下面四个轮子是支撑轮,上面一个轮是驱动轮,驱动轮与步进电机之间由减速器连接,步进电机驱动轮行走,在运行过程中,巡检机器人的运动状态包括:前进、后退、停止、制动。而巡检机器人在轨道上平稳运行是能否开展智能巡检的关键,因此选择的电机需要提供足够转矩,来驱动机器人运行,克服各类阻力。
步进电机是一种将电脉冲转换为机械角位移的执行元件,其角位移量和输入脉冲的个数成正比,在时间上与输入脉冲同步[2]。在开环工作方式下能够达到很高的定位精度,且低速运行时又可输出很大的转矩,因此在运动控制中得到了广泛的应用[3]。但是步进电机的驱动系统存在非线性、时变、干扰等问题,传统的PID 控制不能够达到很好的控制效果,电机易失步,产生累积误差,导致机器人运行不稳定。因此针对巡检机器人运动控制系统,本文设计了模糊PID 控制器来提高步进电机驱动系统的控制性能。
1 驱动系统数学模型
在本控制系统中,采用两相混合式步进电机作为系统的驱动电机。在不考虑定子极间和端部的漏磁、永磁体回路的漏磁,忽略磁滞涡流和饱和影响,忽略定子线圈自感的谐波分量的基础上[4],建立电机动态数学模型。步进电机原理图如图1所示。
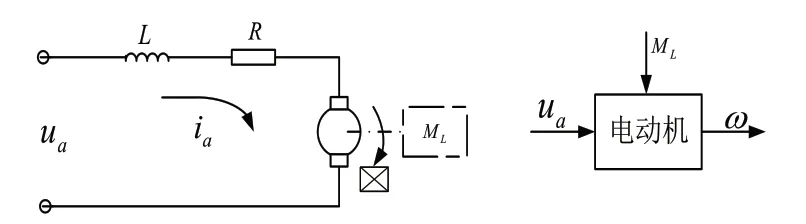
图1 步进电机原理图Fig.1 Schematic diagram of the stepper motor
根据克希荷夫定律:

根据负载及电机特性:
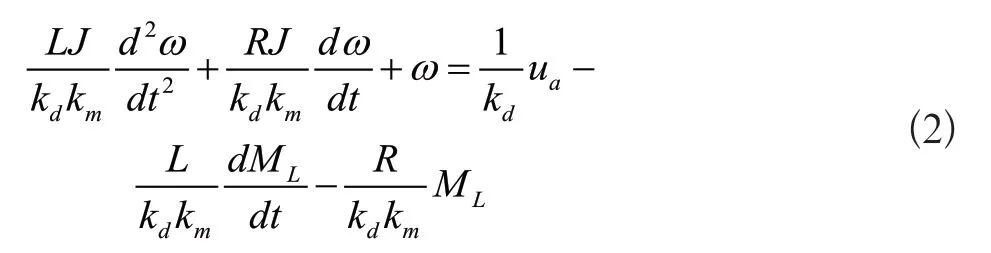
经过拉普拉斯变换,可得电机转速,电机传递函数为:

式中:J=0.01,R=1.5,L=0.01;设ML(s)=0,放大系数Kv=5,减速比Kr=5,传感器L=1。电压为输入,转速为输出,开环传递函数为:
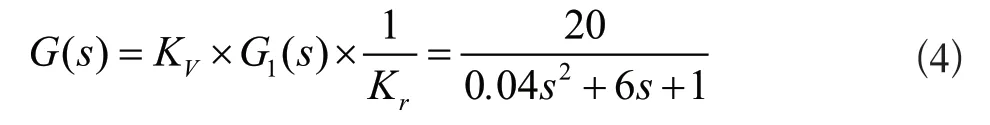
2 传统PID 控制算法
传统PID 控制由比例、积分、微分环节组成。它是一种线性控制器,输入为当前系统的误差e(t),输出为:
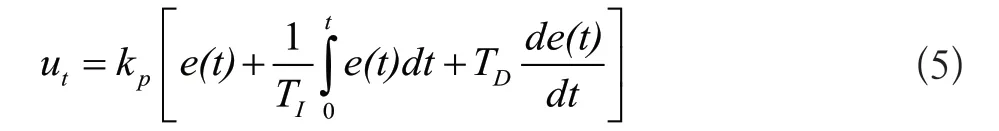
其中Kp为比例系数、TI为积分时间常数、TD为微分时间常数[5]。PID 控制器的结构图如图2所示。
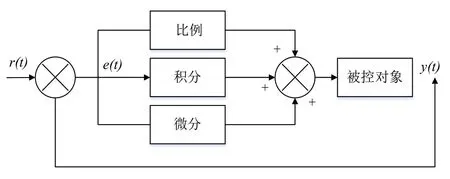
图2 传统PID 控制器结构Fig.2 Structure of traditional PID controller
PID 控制器的参数整定方法为经验凑试法。观察系统响应情况,先比例,后积分,在微分[5]。首先将P 值放在较小的位置,然后逐渐增大,观测曲线的变化;在整定比例参数之后,将比例值缩小,不断进行调整;最后在整定微分值。通过上述方法最终调整PID 参数为Kp=7,Ki=1.6,Kd=0.1。在计算机控制中应当将公式离散化,离散化的数学表达式如下:
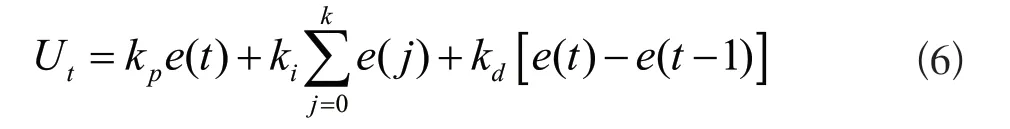
3 BP-PID 控制算法
BP 神经网络是目前应用比较广泛的神经网络结构,具有很好的逼近非线性映射能力BP 神经网络算法分为正向传播和反向传播两部分。BP 神经网络的结构图如图3所示。
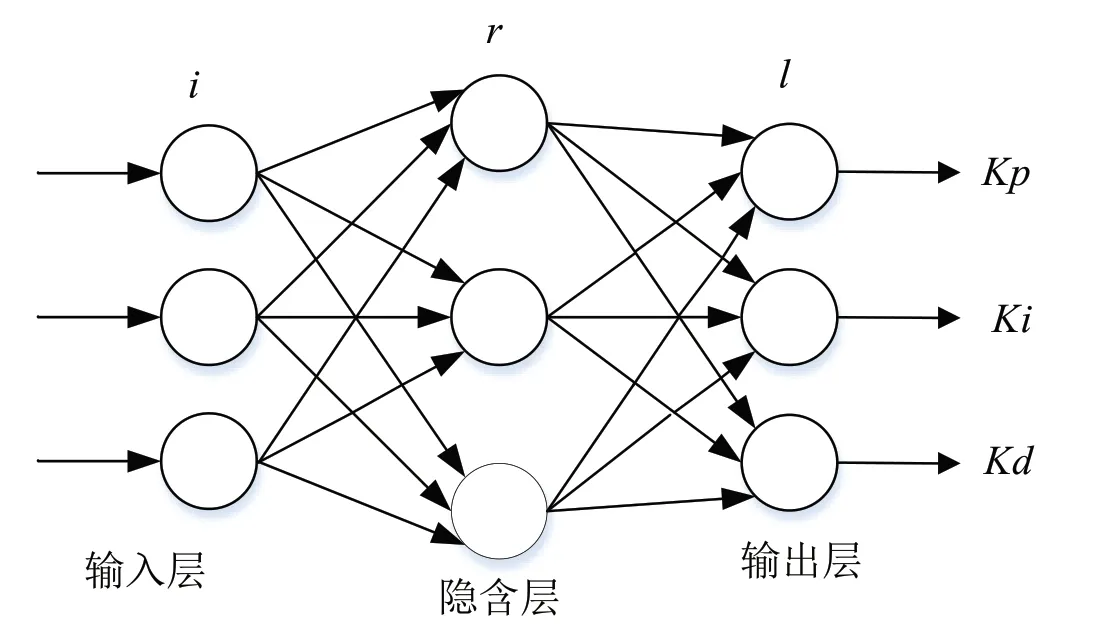
图3 BP 神经网络结构图Fig.3 Structure diagram of BP neural network
BP-PID 控制器是在传统PID 的基础上再加入BP 神经网络,在这个控制器中,PID 的作用是实现对被控对象的闭环控制,BP 神经网络是为了实现对PID 参数的在线调节。如图4所示。

图4 BP 神经网络控制器结构图Fig.4 Structure diagram of BP neural network controller
确定BP 网络的结构,确定输入层的节点数M、隐含层节点数Q,给出各层加权系数ωij和ωli,选定学习速率η和α为惯性系数[6];采样得到输入和输出,计算此时的误差值error;计算神经网络各层神经元的输入、输出,输出层的输出就是PID 控制器的三个参数;根据PID 控制器计算系统的输出U(k);进行神经网络的学习,在线调整加权系数,实现PID 控制器的自适应调整。
4 模糊PID 控制算法
在控制系统中,模糊控制可以将非定量用模糊集来表示,把这些模糊规则以及有关信息作为知识放进计算机知识库中,通过模糊推理可以实现对参数最佳的调整。将传统PID 和模糊控制相结合,可自动实现对PID 参数的最佳调整。如图5所示为模糊PID 控制器结构图。
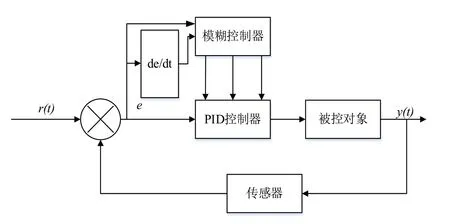
图5 模糊PID 控制器结构Fig.5 Structure of fuzzy PID controller
将模糊控制技术与PID 控制相结合构成模糊PID 控制,应用模糊推理的方法实现对PID 的参数在线自整定。在模糊PID 控制中,输入为偏差e和偏差变化率ec,输出为ΔKp、ΔKi、ΔKd,输入和输出之间有一定的模糊关系。偏差和偏差变化率在运行过程中会不断改变,利用模糊关系实时对三个参数进行调整[7]。
(1)确定控制器的输入和输出变量。
(2)设计模糊控制器的规则。根据输入和输出之间的关系,结合实际经验,建立模糊控制规则表,隶属函数为三角形函数。
(3)确立模糊化和非模糊化的方法。其中模糊化就是将精确量离散化。解模糊化的方法是重心法[8]。
(4)选择模糊控制的输入、输出变量的论域。选择e的论域为[-1 20],ec 的论域为[-15 2],Δkp的论域为[-1.5 1.5],Δki的论域为[-0.1 0.5],Δkd的论域为[-0.1 0.1]。模糊子集为e,ec={NB,NM,NS,O,PS,PM,PB},其中子集分别表示负大,负中,负小,零,正小,正中,正大[9]。
(5)模糊推理及解模糊化。通过采用模糊语句,将模糊规则写入,形成49 条控制语句。通过Mamdani 法进行推理[10]。
输入对输出影响关系的空间曲面图如图6-图8所示。
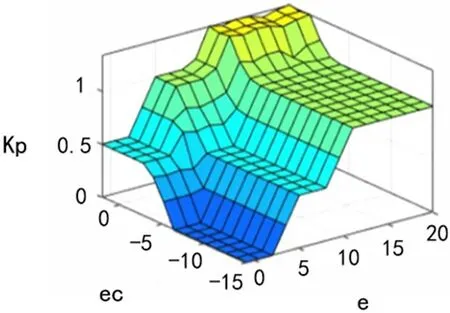
图6 kp 空间曲面图Fig.6 kp spatial surface graph
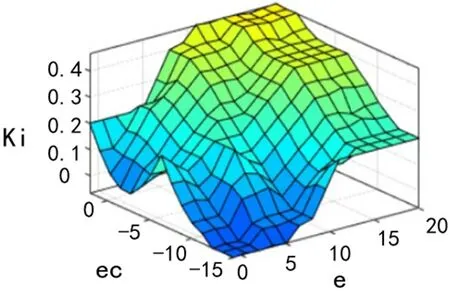
图7 ki 空间曲面图Fig.7 ki spatial surface graph
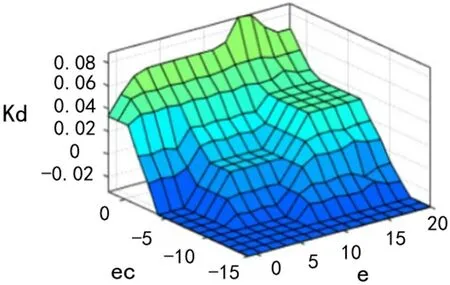
图8 kd 空间曲面图Fig.8 kd spatial surface graph
将传统PID 控制器、BP-PID 控制器与本文所设计的模糊自适应PID 控制器进行仿真比较,将上文所推导的步进电机传递函数作为被控对象,在仿真软件中进行搭建。仿真搭建模型如图9所示。

图9 三种控制器仿真对比图Fig.9 Simulation comparison of three controllers
设定采样时间为1s,对PID 控制器、模糊PID 控制器、BP-PID 神经网络控制器的性能进行仿真对比验证,如图10所示。
通过图10可知模糊PID 闭环控制算法与传统PID 算法和BP-PID 算法控制有较大的优势。仿真结果表明在时间设定为1s 的情况下,PID 控制器的系统响应时间为0.3s,BP-PID 控制器的系统响应时间为0.2s,模糊PID控制器的系统响应时间为0.08s,根据以上对比,发现模糊PID 控制器系统响应速度最快,效果最好。
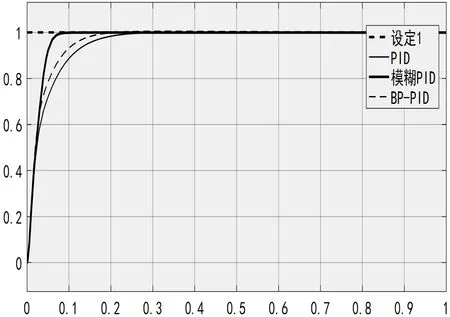
图10 PID、BP-PID 和模糊PID 仿真曲线对比Fig.10 Comparison of PID、BP-PID and fuzzy PID simulation curves
5 结论
本文针对巡检机器人步进电机设计了模糊PID 控制器,并将传统PID 控制器、BP-PID 控制器与模糊PID控制器进行仿真分析,从仿真结果看出模糊PID 闭环控制算法相较于其他控制算法在系统响应速度和精度方面具有明显优势。因此可以将模糊PID 控制器应用于巡检机器人运动控制系统。
