基于小波变换的雷达目标识别方法探讨

常州机电职业技术学院 金舒萍 汤雪彬

的系数既表示了信号在某一时间上变化的情况，又表示了信号在某个特定的时间范围内的频率的变化情况[3，4]。

实际运用中，连续小波变换必须离散化。在连续小波函数中把它的尺度参数a和平移参数b离散化为a=a0j，这里j∈Z，扩展步长a0≠1为固定值。通常，为方便起见，总是假定a0＞1。所以对应的离散小波函数写作如式（5）所示：

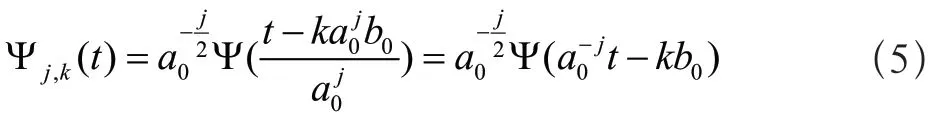
则离散化的小波系数可表示为如式（6）所示：

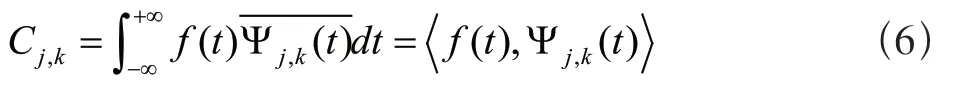
其重构公式如式（7）所示：

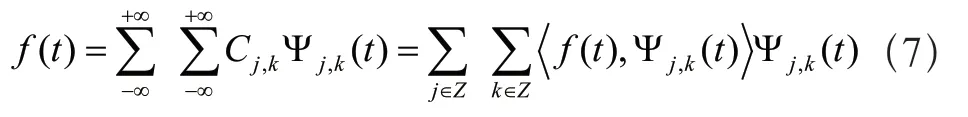
然而，连续小波变换需要进行大量的运算，离散小波变换中任取的小波函数没有正交性，这都给信号的分析带来了极大的不便。1986年，Meyer 提出的一组伸缩和平移构成L2(R)的标准正交基小波，让小波变换在时域和频域领域的应用得到了比较大的发展。1988年，在构造正交小波基础上，S.Mallat 在提出了多分辨分析的概念，给出了通用的类似FFT 算法的正交小波构造方法，即小波变换的快速算法——Mallat 算法[5，6]。

假设空间L2(R)中的一列闭子空间{j}jZ V∈满足条件：单调性、逼近性、伸缩性、平移不变性和Riesz 基存在性，则这一列子空间构成了空间L2(R)上的多分辨分析。Vj称为尺度空间，Wj=Vj⊥称为小波空间，且有

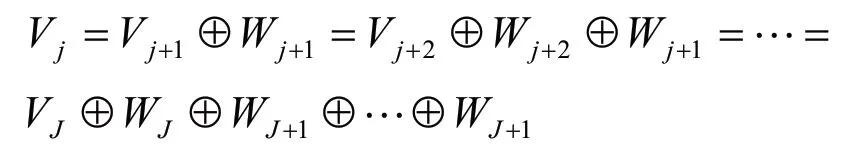
则对于φ∈V0，Ψ∈W0有下面的双尺度方程成立如式（8）所示：

由上式，对于能量有限信号f(t)∈VJ=VJ+1⊕WJ+1可以表示成如式（9）所示：

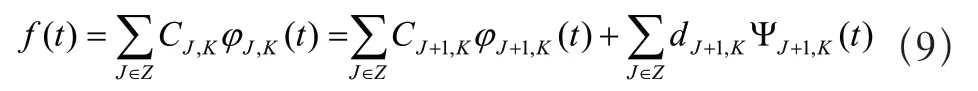
由双尺度方程，可以得到下面的分解公式如式（10）所示：

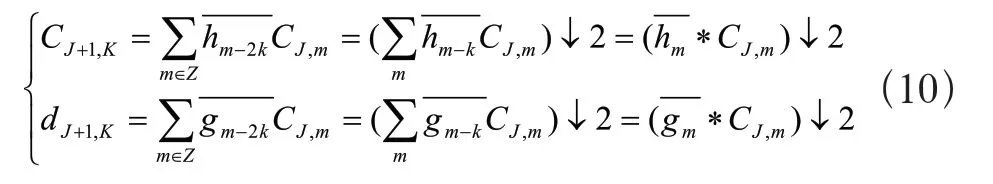
其中*为卷积符号。

在分解公式中可以看到，尺度空间和小波空间的系数的计算可以通过类似于信号处理系统中的滤波器对输入信号的变换来实现（通过低通滤波器得到Cj，通过高通滤波器得到dj）。对得到的尺度空间的系数继续进行分解，则可得到不同尺度下的系数（Cj）和相应的小波系数（dj）。因而系统对信号的分析性能就体现在尺度函数（φ）和小波函数（Ψ），也即滤波器组冲击响应（h、g）的选取上。

2 雷达目标的识别

雷达目标识别的过程就是信号处理器从系统接收到的信号中去除杂波和干扰、提取目标的回波信息并从该信息中判断目标属性的过程。不同目标识别的方法机理各不一样，但是对回波信息提取上有着相似的目的和要求，现将使用极化信息进行识别目标作为例子，说明小波变换在其中的重要作用[7，8]。

要获得目标的极化信息关键在于目标散射矩阵的求解，在发射一组正交极化信号的情况下，根据接收到的目标回波的极化方式（Er1、Er2），可以用如式（11）所示的式子进行极化散射矩阵（S）的求解。

因而回波能量计算的准确与否决定了极化散射矩阵的求解精度。在雷达系统中，目标的回波能量是与目标距离的四次方成反比的。所以在对极化散射矩阵进行求解之前，信号处理器需完成对目标距离的判断、回波能量的幅度信息获取、回波能量的归一化这几步工作。

以发射单矩形脉冲为例，目标的回波是一个单矩形脉冲，但是被噪声所干扰，信号处理器不能直接进行识别。注意到噪声信号的频谱是分布在全频域的，若通过傅立叶变换滤除信号中一部分频率并保留回波脉冲的范围频率，则在这个频率范围上，噪声未被除去，它的作用使信号处理器对回波幅度的判断不再准确，影响了后面对极化散射矩阵的求解。若对信号进行基于小波变换的多分辨分析，在特定的尺度下，分解出的小波系数就表征了目标回波的那部分信息，包括时间和幅度信息。从而信号处理器可以迅速且准确地对回波信息进行获取，减少了处理时间，提高了系统的性能。

笔者在Matlab 中使用db6 小波工具进行回波分析的情况。系统发射一组正交极化信号（水平、垂直），通过正交的两路通道接收。目标假定为球距离为2km，系统信噪比为5dB，回波能量均已归一化。在系统为低信噪比的情况下，对回波进行小波分解后，对其尺度系数或小波系数进行门限检测，可显著降低虚警概率。对于幅度值的获取，可以从目标回波点左右的正负脉冲幅度之和来得到，这种情况下去掉了脉冲中的高频成分，可以得到相对准确的回波幅度。在求得回波信号的幅度之后，代入计算S 的公式，则可得到目标的散射矩阵，从而在对散射矩阵的分析中完成对目标的识别，验证了小波变换有效提高了雷达目标识别精度。

3 结语

小波变换在时域和频域展开的良好信号分析特性，决定了其在雷达信号分析上具有广阔的应用。对于雷达获取目标信息来说，小波变换可以实现对接收信号的精确分析，显示了其较普通信号分析工具的优越性，但是使用小波分析必然会带来信号处理器结构的复杂，造成实现难度的增大，这对于设计者来说是一个巨大挑战。然而不可否认的是，在处理复杂雷达信号以及复杂目标识别的应用中，小波变换有着广阔的前景。