连续工况下基于PID+LQR算法的自动驾驶车辆横纵向耦合控制

2022-12-05余米森钱玉宝黄华宝王紫涵

科学技术与工程 2022年30期

余米森，钱玉宝*，黄华宝，王紫涵

(1.长江大学机械工程学院，荆州 434023； 2.长江大学新能源特车研究所，荆州 434023)

随着社会的发展，汽车保有量与日俱增，随之而来的交通安全、效率等问题也日益严峻，自动驾驶技术成为比年来汽车工程领域的研究热点[1-2]。车辆控制作为自动驾驶的关键技术之一[3]，相关研究主要包含纵向控制、横向控制及横纵向耦合控制[4]。

自动驾驶车辆上层控制器各功能的实现需要依托于底层控制器[5]，而底层控制主要通过对车辆的横向和纵向来控制车辆。如何保证车辆能够精确地沿着由决策规划系统制定的路径行驶，且跟踪精度能够达到期望值，这是自动驾驶车辆控制方面的一个难题[6]。若对车辆横纵向运动进行单独控制，由于运动方向之间的相互作用，纵向控制可能会带来横向扰动等，横纵向运动的相互干涉会导致整车控制系统的控制精度下降，车辆主动安全性得不到保障[7]。

自动驾驶是一项典型的“智能”技术，但它非天生聪明[8]。随着对自动驾驶车辆控制领域的进一步研究，出现了一些优化型横纵向控制算法[9]。文献[10]设计了一种自动驾驶车辆纵向自适应优化控制算法，而文献[11]则提出了一种带有前馈控制的改进型线性二次型调节(linear quadratic regulator，LQR)横向运动控制方法。文献[12]根据车辆与目标路径的横向误差和角度偏差提出了基于速度自适应预瞄无模型转向控制算法；文献[13]则对大曲率且多变的混合道路工况下横向控制系统的自适应性和控制精度不足的问题提出了一种横向可拓预瞄切换控制方法。

文献[14]为插电式混合动力汽车提出了模型预测控制(model predictive control，MPC)算法；而文献[15]为实现多辆震源车的安全自动跟随行驶，提出融合比例积分微分(proportional integral differential，PID)和MPC的控制算法；基于非线性模型预测控制算法(nonlinear model predictive control，NMPC)，文献[16]提出一种路径跟踪器的设计及实现方案。随着芯片计算能力的提高，文献[17]采用无模型强化学习算法中的REINFORCE算法和神经网络技术研究无人驾驶车辆变道控制策略。同时，为规避决策算法的复杂性及带来的社会伦理问题，有研究人员开展了基于图像的端到端深度学习模型来控制自动驾驶系统的研究[18-19]。

然而，以上文献大都是对自动驾驶车辆的横向运动和纵向运动进行单独研究来实现对车辆的控制，对于车辆横纵向耦合运动的控制策略、算法及效果的研究和验证较少。因此，现基于PID+LQR算法来实现对自动驾驶车辆的横纵向耦合控制，并借助联合仿真测试平台来验证横纵向耦合控制策略的效果。为自动驾驶车辆横纵向耦合运动的控制策略及控制算法等研究提供参考。

1 模型简化与动力学方程

依据物理系统建立的模型主要有车辆动力学模型和轮胎受力模型等。本文研究采用的是二自由度动力学模型。

1.1 汽车模型简化

本文研究的对象是前轮转向汽车。模型简化过程：①忽略转向系统的影响，直接以前轮转角作为输入；②忽略悬架作用，车身只做平行于地面的平面运动，即汽车沿z轴的位移，绕y轴的俯仰角以及绕x轴的侧倾角均为零；③汽车的前进速度不变；④侧向加速度ay<0.4g(g为重力加速度)，轮胎的侧偏特性处于线性范围；⑤忽略空气动力学的作用；⑥忽略左右轮胎由于载荷变化而引起的轮胎特性的变化及轮胎回正力矩的作用。汽车被简化为只有沿y轴的侧向加速度和绕z轴的横摆运动的线性二自由度两轮汽车模型。简化后的汽车模型如图1所示。

1.2 车辆动力学方程

完全基于几何关系而不考虑影响运动的力而建立的运动学模型不适用于高精度运动控制要求，所以需要研究用于车辆侧向运动的动力学模型。

基于二自由度“自行车”模型，两个自由度分别用车辆侧向位移y和车辆横摆角φ表示。忽略路面坡度，沿y轴方向应用牛顿第二定律：

may=Fyf+Fyr

(1)

式(1)中：ay为车辆在质心处沿y轴的惯性加速度。

(2)

(3)

由绕z轴的转矩平衡可得车辆横摆动力学方程为

(4)

当侧偏角较小时，轮胎的侧向力与侧偏角成正比。轮胎的侧偏角定义为轮胎平面方向与轮胎速度矢量之间的夹角。前轮侧偏角为

αf=δ-θvf

(5)

αr=-(0-θvr)

(6)

式(5)中：θvf为车辆前轮速度矢量与车辆纵轴之间的夹角；θvr为后轮速度矢量与纵轴之间的夹角。

车辆的前轮侧向力可表示为

Fyf=2Cαf(δ-θvf)

(7)

同理，后轮侧向力为

Fyr=2Cαr(θvr)

(8)

式中：Cαf、Cαr分别为前、后轮侧偏刚度。

(9)

(10)

(11)

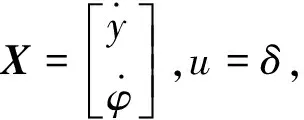
(12)

式(12)中：X为状态变量矩阵；A为状态变量系数矩阵；B为控制变量系数矩阵；u为控制变量。因此，可以通过控制δ来实现对y和φ的控制。

2 横纵向联合控制

横向控制是自动驾驶车辆控制中的难点，主要负责方向盘的控制。纵向控制主要是负责自动驾驶车辆油门和刹车的控制。

2.1 横向控制策略

算法的输出为

u=-Kerr+fc

(13)

控制过程主要分为4步：①向A、B计算模块输入整车参数和车辆纵向速度vx计算出矩阵A、B；再联合对角矩阵Q、R，借助LQR计算模块得出比例系数矩阵K；②根据车辆位置与状态和轨迹规划点求出车辆误差矩阵err以及投影曲率k；③通过步骤①中求出的K和步骤②中求出的k以及整车参数和vx求出前馈控制量fc；④最后用K、err、αf，通过最终控制计算模块输出u(前轮转角)。控制目标是选择合适的u，使得误差尽可能最小。流程图如图2所示。

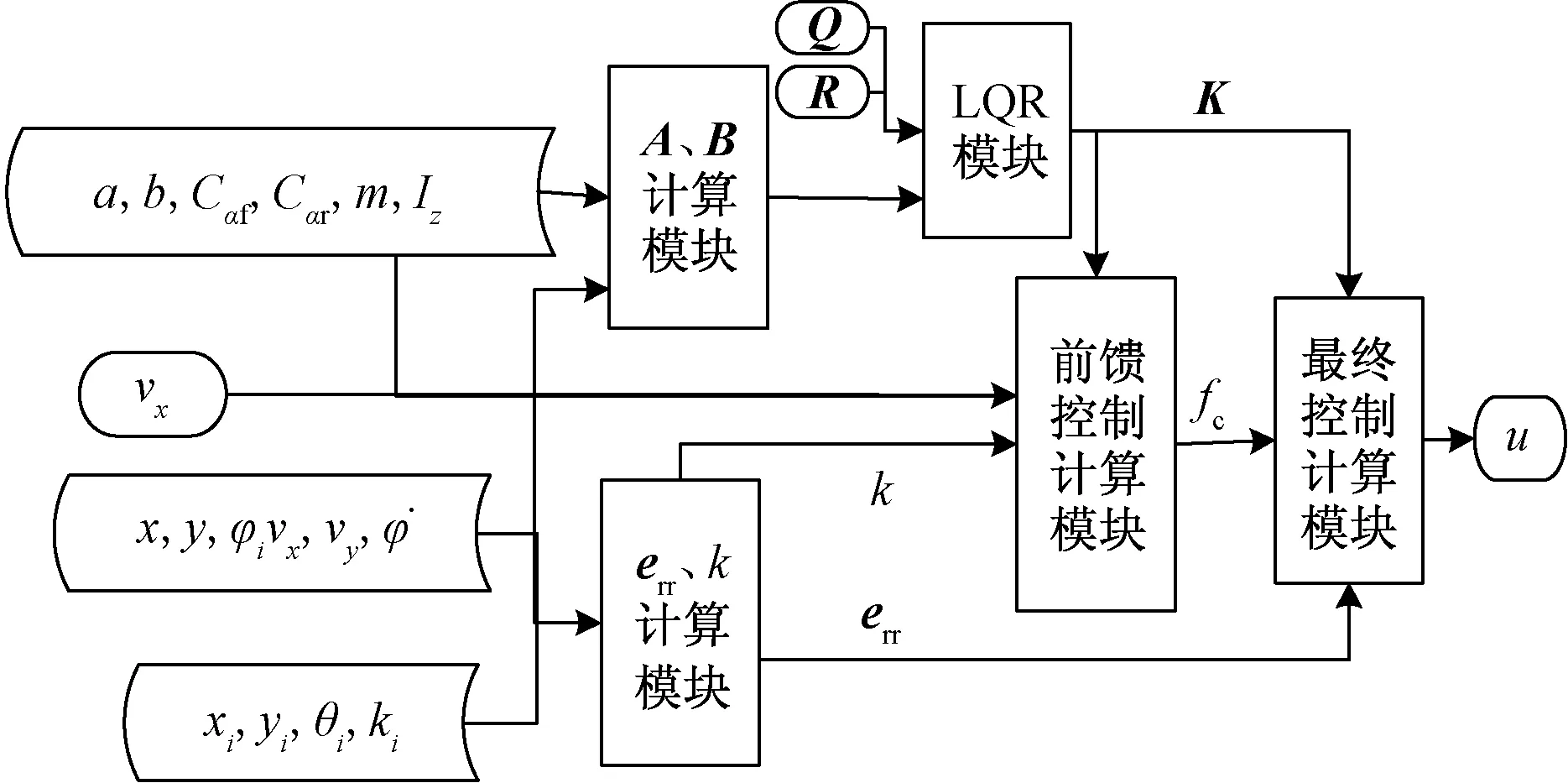
图2 横向控制流程图Fig.2 Lateral control flow chart

2.2 纵向控制策略

目前开发自动驾驶系统所采用的主要是纯电动车辆，所以需要在CarSim中创建一个电机模型。电机模型的基本参数参考比亚迪-唐纯电版，最大扭矩Tmax=385 N·m；最大功率Pmax=180 kW；电机最大转速nmax=4 500 r/min。

自动驾驶汽车的决策通常是依据驾驶员行为规则或是采用自学习算法模仿驾驶员操作经验来实现；有研究提出一种不依赖于大量标注驾驶数据的决策层强化学习方法[20]。本文研究中采用传统的方法来制作油门、刹车标定表，即通过给加速踏板输入不同的角度来得到不同的速度v和加速度a曲线，再整合速度和加速度即可得到v-a曲线。

纵向控制流程如图3所示。

es为纵向误差;vp为规划车速；ap为规划加速度；为基于Frenet坐标系的车速；thr(throttle)为节气阀开度系数；bra(brake)为制动踏板压力系数图3 纵向控制流程Fig.3 Longitudinal control flow

纵向控制采用双PID控制的策略，第一个PID为位置控制器，即处理车辆期望位置与实际位置之间的纵向误差es；第二个PID为速度控制器，接受前PID控制器对纵向误差处理结果的输出和车辆当前位置速度及规划模块给出的速度，并将处理结果传递给下一个模块。车辆油门刹车控制模块依据制作的油门刹车标定表来控制车辆的加减速，从而实现对车辆的纵向控制。

2.3 横纵向控制算法

2.3.1A、B计算模块

将Cartesian(笛卡尔)坐标系变换为Frenet坐标系。自动驾驶控制算法理论起点公式为

(14)

(15)

=vycos(φ-θr)+vxsin(φ-θr)

(16)

认为φ-θr很小，根据等价无穷小可得

(17)

令ed=d,eφ=φ-θr，则可得

(18)

(19)

表达式可简写为

(20)

式(20)中：err为新的状态量，表示车辆实际位置与规划轨迹之间的横纵向误差；A、B分别为更新后的状态量与控制量系数矩阵。

2.3.2 LQR模块

为让误差尽可能最小，令J为代价函数。

(21)

(22)

代价函数最小，即式(22)在约束条件式(20)下最小。U为控制量u在控制序列中的数组，对角矩阵Q、R分别为误差权重矩阵和控制量权重矩阵。

因为A、B只与整车参数和vx有关，而整车参数可近似认为不变，所以A、B只和vx有关。

K=lqr(A,B,Q,R)

(23)

经lqr数值计算可知，可得vx和K的对应表。

2.3.3err、k计算模块

在规划轨迹点的车辆状态参数为

(24)

遍历xr、yr找到与x、y最近的规划点，并记该点的序列为dmin。

(25)

(26)

(27)

θr=θmin+kdmines

(28)

(29)

(30)

kr=kdmin

(31)

2.3.4 双PID模块

控制模块中的两个PID分别为位置PID和速度PID。比例系数Kp的作用是加快系统的响应，提高系统的调节精度；Kp越大车辆的纵向行驶轨迹就越快的逼近规划轨迹，但Kp过大会产生超调，甚至会导致系统不稳定。积分系数Ki的作用是消除系统的稳态误差，使纵向控制系数无限的逼近期望值；Ki越大系统的稳态误差消除越快，但过大的Ki会在初期产生积分饱和现象，从而引起较大的超调。微分系数Kd的作用是改善系统的动态特性，抑制PI对车辆纵向控制时产生的超调。原理如图4所示。