基于相场法的岩石三点弯曲细观破坏数值模拟

2022-12-05李明耀李绍金左建平王智敏彭磊薛喜仁

科学技术与工程 2022年30期

李明耀, 李绍金, 左建平*, 王智敏, 彭磊, 薛喜仁

(1.中国矿业大学(北京)煤炭资源与安全开采国家重点实验室，北京 100083; 2.中国矿业大学(北京)力学与建筑工程学院，北京 100083)

岩石材料在复杂环境下的变形、破坏及失稳等力学行为对岩体工程结构的强度和安全至关重要。岩石内部裂纹的萌生、扩展和贯通等力学行为是其中的关键力学问题，是预测岩体工程的强度和稳定性的关键因素之一，也是一直以来中外学者研究的热点和难点。目前，采用数值模拟方法是研究岩石内部裂纹扩展行为的重要手段。

目前，针对裂纹扩展问题发展提出了不同的数值模拟方法，如有限元法(finite element method)[1]、扩展有限元法(extended finite element method)[2]、离散元法(discrete element method)[3]、位移不连续法(displacement discontinuity method)[4]、相场法(phase field method)[5]和弥散裂纹法(smeared crack method)[6]等。这些数值方法主要可分为离散方法和连续方法两大类。离散方法将裂纹视为真实的或等效于物理情况的强不连续性裂纹。如余华中等[7]基于颗粒离散元颗粒流程序研究节理的宏细观剪切力学行为以及不同法向应力作用下微裂纹的发育及演化规律；Alneasan等[8]基于DDM模拟和分析混合加载模式下断裂参数对岩石裂纹扩展的影响；杨善统等[9]利用随机分布Voronoi图生成不同裂缝产状岩石模型，采用刚性弹簧方法模拟了非贯通裂隙岩石细观裂纹起裂和扩展过程。离散方法能够较为真实地反映裂纹形态，但需要先进的计算能力才能处理较为复杂的裂纹扩展问题，特别是对于流体流动具有强非线性耦合问题的水力压裂等[10-11]。连续方法则将裂纹视为连续分布形式的连续体，如Li等[12]基于FEM传统重新网格划分方法模拟和预测岩石在混合模式断裂试验下裂纹扩展的规律。XFEM模拟裂纹可以避免重画网格从而得到了广泛的应用，如Yan等[13]基于扩展有限元法研究了含预制裂纹的岩体中裂纹萌生、扩展和贯通的规律；牛骏等[14]将扩展有限元与嵌入式离散裂纹模型耦合的方法模拟页岩水力压裂，得到了页岩水力裂缝内部开度的动态变化以及流体压力对裂纹的影响。连续方法在连续体公式中规范了裂纹的不连续性，以避免捕获与裂纹萌生、转向和分叉相关的路径演变的困难，通常以直接的方式应用于计算。数值方法处理上的优势使得连续方法近年来得到了广泛的应用，但连续方法的缺点在于不可避免地难以获得裂缝宽度和表面等信息。

近年来，相场法因其在模拟裂纹扩展方面的优势被越来越多的学者关注。相场法从最初Francfort等[15]提出的断裂变分理论以及Bourdin等[16-17]提出裂纹正则化理论，到Miehe等[18-19]提出了应变谱分解方法和交替迭代法后，被广泛应用于模拟裂纹扩展问题。相场法主要通过一系列的微分方程，引入序参量，利用弥散的方式描述裂隙边界，避免了显式追踪裂纹面，用序参量的自动演化获取裂纹的路径及位置，在模拟裂纹起裂、扩展、分叉和多裂纹相互贯通等现象具有一定优势，为研究复杂裂隙扩展问题提供了一种重要手段。

Molnar等[20]提出基于扩散裂缝的速率无关变分原理的相场法应用于研究具有复杂初始细观结构的岩石材料内部的裂纹扩展问题。在此基础上，现通过模拟含偏置缺口玄武岩的三点弯曲实验，研究不同偏置距离缺口的玄武岩内部裂纹扩展过程及其影响因素，通过与室内试验的宏观和细观结果对比分析表明，相场法能很好地模拟和预测具有复杂初始细观结构的岩石材料的内部的裂纹扩展问题，为研究岩石内部裂纹扩展问题提供一种重要手段。

1 相场法的基本理论及数值实现

相场法是在经典Griffith断裂力学理论的基础上，利用最小能量变分原理来克服传统断裂力学理论框架需要复杂的裂纹扩展判据的不足，是对传统断裂力学理论的继承和发展。相场法理论认为一个弹性体V，其总势能Π由弹性应变能和裂纹表面能两部分组成：

(1)

式(1)中：V⊂Rn,其中n为维度，n=1，2，3；ψe为弹性应变能密度；Γ为裂纹表面；ε(u)为应变张量；Gc为材料的临界能量释放率。变分原理认为，裂纹的起裂、扩展和分叉等行为都应使总势能取最小值且遵循不可逆条件。

为了描述裂纹的分布情况，引入一个相场变量d(x)∈[0,1]，表示材料的损伤值，当d=0时，表示材料完好，当d=1时，表示材料完全破坏，即断裂。裂纹表面函数Γl(d)可以表示为

(2)

式(2)中：γ(d,∇d)为裂纹表面密度函数，形式为

(3)

式(3)中：lc为特征长度参数，控制裂纹的宽度。根据Miehe等[18-19]的研究成果，将式 (2) 改写成欧拉变分形式

(4)

式(4)中：W={d|d(x)=1,∀x∈Γ}。

弹性应变能密度ψe可以表示为

ψe(ε,d)=g(d)ψ0(ε)

(5)

式(5)中：ψ0(ε)为弹性应变能密度；g(d)为材料刚度削减函数，g(d)=(1-d)2+κ，其中参数κ为了保证当材料局部发生完全破坏(d=1)时数值方法的稳定性。对于线弹性完好材料，弹性应变能密度可以表示为

(6)

式(6)中：C0为材料的弹性张量；应变张量ε=[(∇u)T+∇u]/2。由于损伤的产生，弹性应变能会随着损伤的演化而衰减，通过对应变能密度求解应变张量的一阶导数可得应力张量为

σ=g(d)σ0=[(1-d)2+κ]σ0

=[(1-d)2+κ]C0:ε

(7)

弹性张量也可以表示为

C=g(d)C0

(8)

由此可见，由损伤变量直接影响着材料的弹性张量和应力。

由于在有限元框架下由相场法直接求解出节点位移和相场具有强非线性，求解需要较多的迭代步，计算效率低。为了提高求解效率，可以对位移场和裂缝场解耦求解。研究表明，这种求解方法的计算效率可以大幅提升，同时可靠性高。因此，本文研究中采用Molnar等[20]中的解耦数值方法，在ABAQUS有限元软件中通过编写用户子程序UMAT和UEL来实现基于相场法的裂纹扩展数值模拟。

2 数值验证

为了验证本文数值方法的准确性，首先模拟对比了两个经典数值实验：单边缺口拉伸试验和对称三点弯试验。通过对比裂纹扩展过程和加载位移曲线，验证了本文采用的数值方法能够准确、合理地模拟裂纹扩展过程。同时，分析了网格数量和长度参数(lc)对实验结果的影响，为后续研究奠定了基础。

2.1 单边缺口拉伸试验

单边缺口拉伸试验是经典的数值实验，该模型的几何尺寸和边界条件如图1(a)所示，尺寸为1 mm×1 mm，其左边中点预置水平裂纹Γ0,裂纹长度为0.5 mm。模型底部固定，在顶部施加竖直向上的位移，左右两侧自由。材料参数为弹性模量E=210 kN/mm2，泊松比ν=0.3，长度参数lc=0.007 5 mm，临界能量释放率gc=0.002 7 kN/mm。前500步位移均匀增量Δu=1×10-4mm，随后位移均匀增量Δu=1×10-5mm完成整个模拟过程，总位移u=0.007 mm。数值分析的网格如图1(b)所示，采用四节点单元，数量约8 000个，在裂纹可能扩展的区域加密网格，加密区网格尺寸h≈0.003 mm。

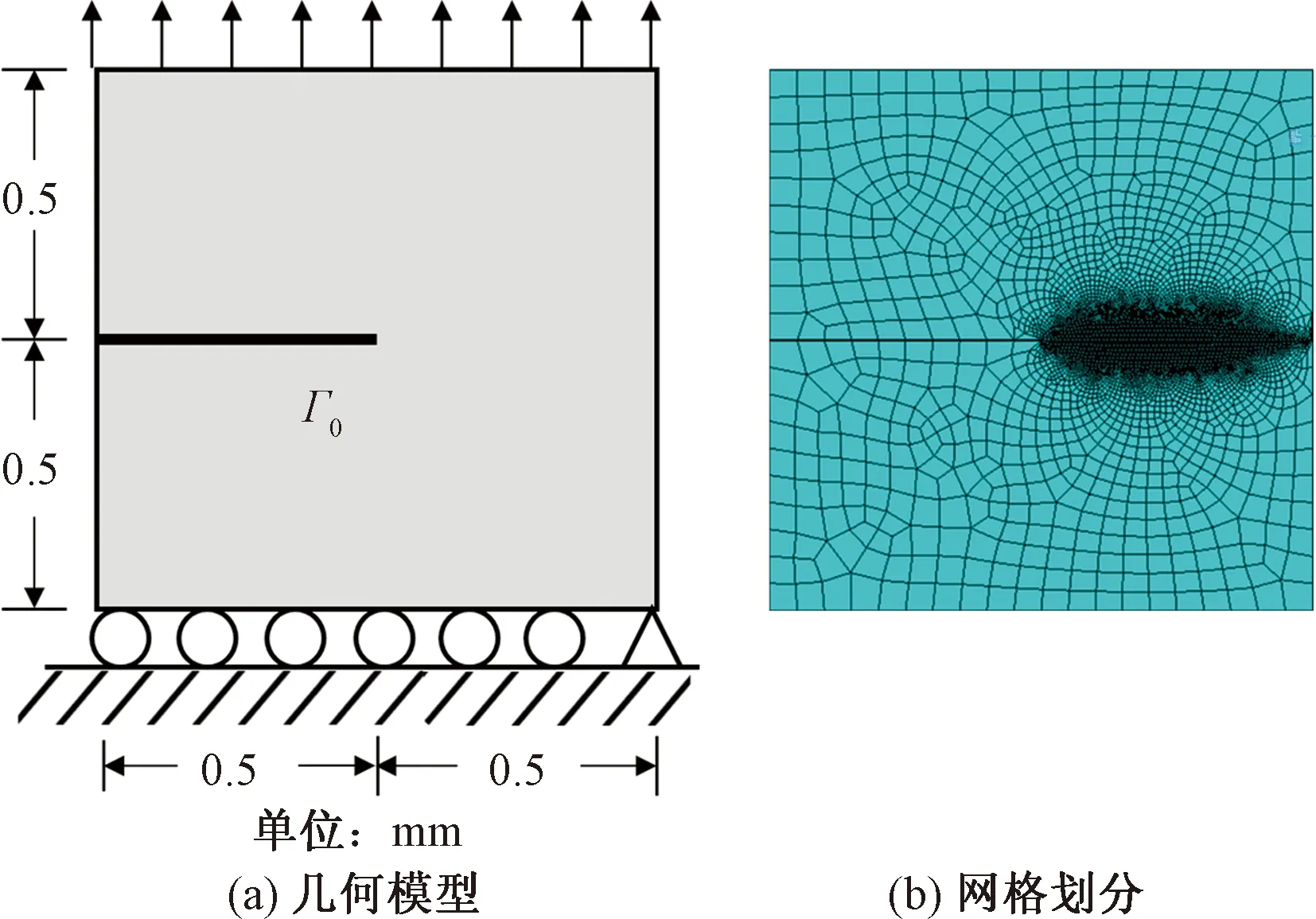
图1 单边缺口拉伸试验模型Fig.1 Single edge notched test model

图2 裂纹路径Fig.2 Crack pattern

图3 力与位移曲线对比Fig.3 Comparison of force-displacement curve with the reference results

图2和图3分别展现本文所模拟的裂纹路径和力与位移曲线与Molnar等[20]的对比结果，可以看出，两者的结果几乎一致，验证了本文采用的数值方法的准确性。

2.2 对称三点弯试验

对称三点弯经典试验的几何尺寸及边界条件如图4(a)所示。弹性模量E=20.8 kN/mm2，泊松比是ν=0.3，长度参数lc=0.06 mm，临界能量释放率gc=5×10-3kN/mm。采用控制位移方式进行加载，前360步位移均匀增量是Δu=1×10-4mm，随后位移均匀增量Δu=1×10-5mm完成整个模拟过程，总位移0.06 mm。同样在裂纹可能扩展的区域进行加密网格，如图4(b)所示，网格采用四节点单元，数量约15 000个，加密区网格尺寸h≈0.006 mm。通过对比发现，本文的数值模拟与Molnar等[20]结果吻合度很高，几乎一致(图5和图6)，进一步验证了本文采用的数值方法的准确性。

图4 对称三点弯试验模型Fig.4 Symmetric three point bending test model

图5 裂纹路径Fig.5 Crack pattern

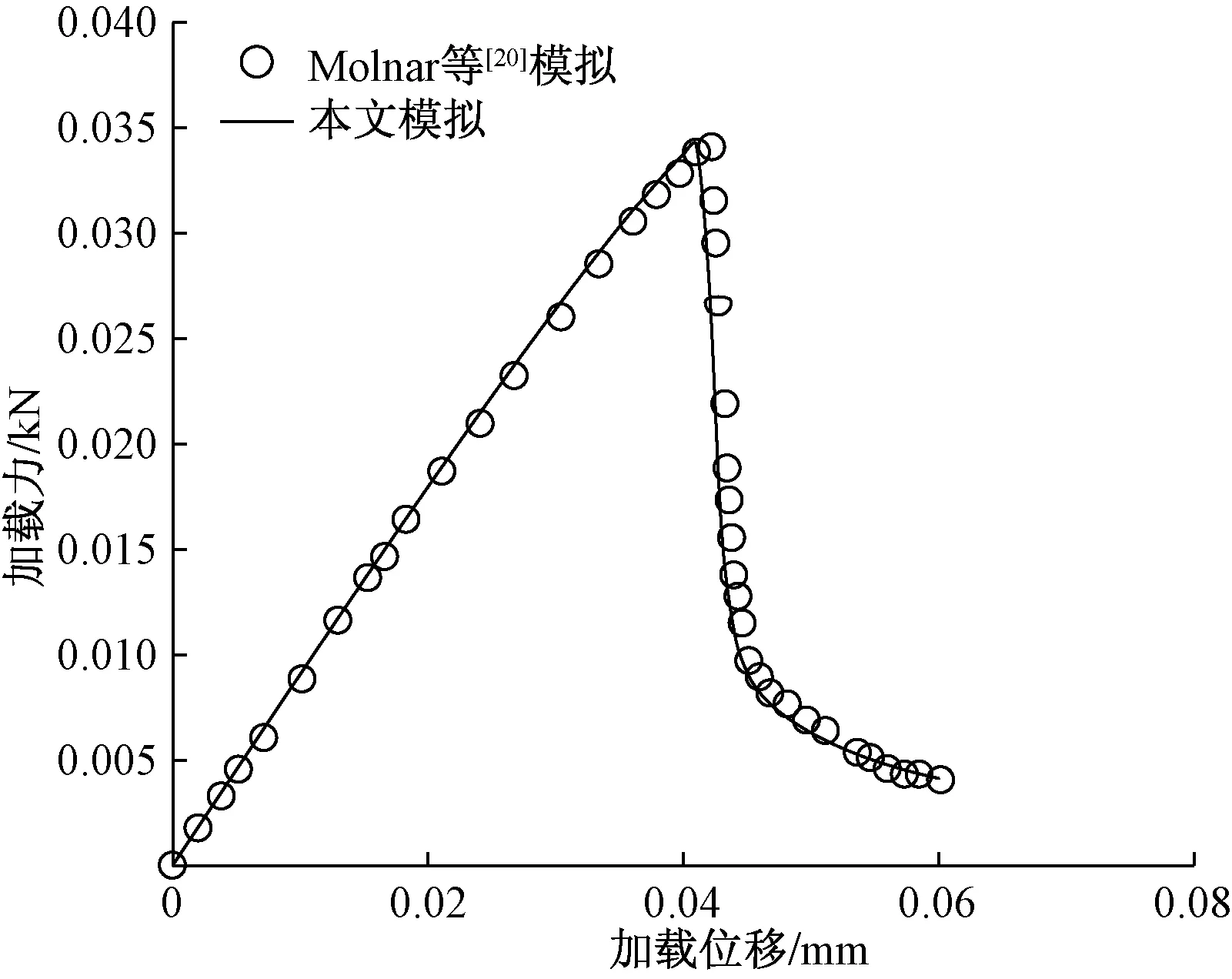
图6 力与位移曲线对比Fig.6 Comparison of force-displacement curve with the reference results

2.3 相场法相关参数的影响分析

2.3.1 网格影响分析

在验证了数值方法准确性的基础上，需要进一步明确不同的网格数对数值模拟结果的影响。以上述对称三点弯试验为分析对象，在其他参数不变的情况下，分别采用3种不同的网格划分方式(网格数分别为6 914、19 358、194 280)，最终模拟的位移载荷曲线如图7所示。结果表明，采用不同网格时的荷载位移曲线基本一致，由此可见，本文采用的相场法对网格数量不敏感。

图7 不同网格的力与位移曲线Fig.7 The force-displacement curves of different mesh

2.3.2 长度参数(lc)影响分析

相场法通过引入正则化参数(即长度参数lc)来弥散裂纹宽度，其选择对数值模拟结果有一定的影响。以对称三点弯实验为例，中心加密区网格最小尺寸为0.015 mm，分别采用长度参数lc为0.015、0.03、0.06 mm进行数值模拟。图8所示为不同长度参数下的裂纹形态。通过对比发现，3个不同参数下，扩展路径几乎一致，但lc越小，所模拟得到的裂纹宽度越接近真实裂纹。参照Miehe等[19]已验证结论，模型参数lc与加密区网格尺寸h的关系可近似表示为lc≥2h。如图9所示为对应的力与位移曲线，可以看出随着长度参数lc的减小，最大荷载与失效位移均在增大。因此，在实际中选取lc时，除了满足lc的定义lc→0以外，还应当通过试验和最小网格尺寸等方式来选取合理的lc，从而保证精度较高、误差较小的裂纹数值模拟结果。

图8 不同长度参数的裂纹形态Fig.8 Crack morphology with different length parameters

图9 不同长度参数的力与位移曲线Fig.9 The force-displacement curves of different length parameter

3 含偏置缺口玄武岩三点弯曲的数值模拟

3.1 试样描述

含不同偏置距离缺口的玄武岩三点弯室内试验[21]的岩样取自北京市门头沟煤矿，埋深约410 m，X衍射分析结果显示该岩样为玄武岩，其内部颗粒成分及体积分数如表1所示。细观试验观测结果显示，玄武岩试样由矿物颗粒随机分布并胶结而成，各矿物成分的弹性参数如表2所示。

表1 玄武岩X射线衍射结果[20]Table 1 X-ray diffraction results of basalt[20]

表2 矿物组分弹性参数[21]Table 2 Elastic parameters of mineral particles[21]

3.2 模型建立及弹性参数

根据矿物颗粒的物理力学性质，将上述矿物成分分为两类：①黏土和绿泥石视为基质；②石英、斜长石，绿帘石视为矿物颗粒。根据Mori-Tanaka方法计算出复合后的颗粒与基质及整个岩样均匀化的弹性参数如表3所示。

实验中模型尺寸及边界条件如图10所示，其中C为偏置距离，预制缺口宽度为0.4 mm。为了减少计算量，数值模拟采用2D平面多尺度模型[23]，首先建立偏置距离2 mm的均质化模型[图11(a)]，研究了裂纹扩展的可能区域[图11(b)]，裂纹可能的扩展路径主要集中在加载点和预制缺口之间的区域。基于此，将模型分为主要区域和次要区域。主要区域为裂纹可能扩展的区域，为了更详细地研究裂纹扩展行为，在该区域建立更能反映岩石真实细观结构的随机矿物颗粒分布于基质的模型，而在次要区域采用均匀化后的均质化模型。图12所示为偏置6 mm多尺度模型的几何尺寸及边界条件，中间为主要区域，两边为次要区域，主要区域的模型按照矿物组分的比例及力学性质生成，次要区域参数为均质后的参数。

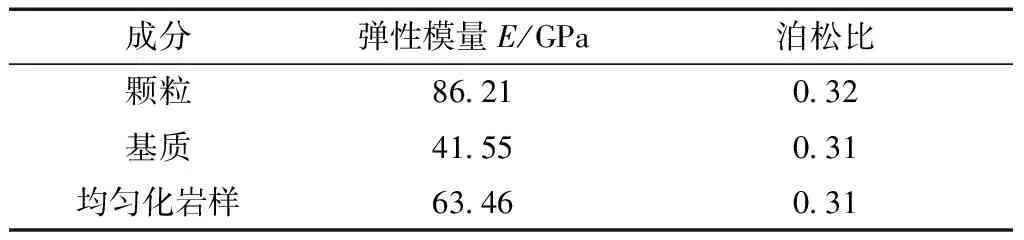
表3 均匀化弹性参数[22]Table 3 The homogenized elastic parameters[22]

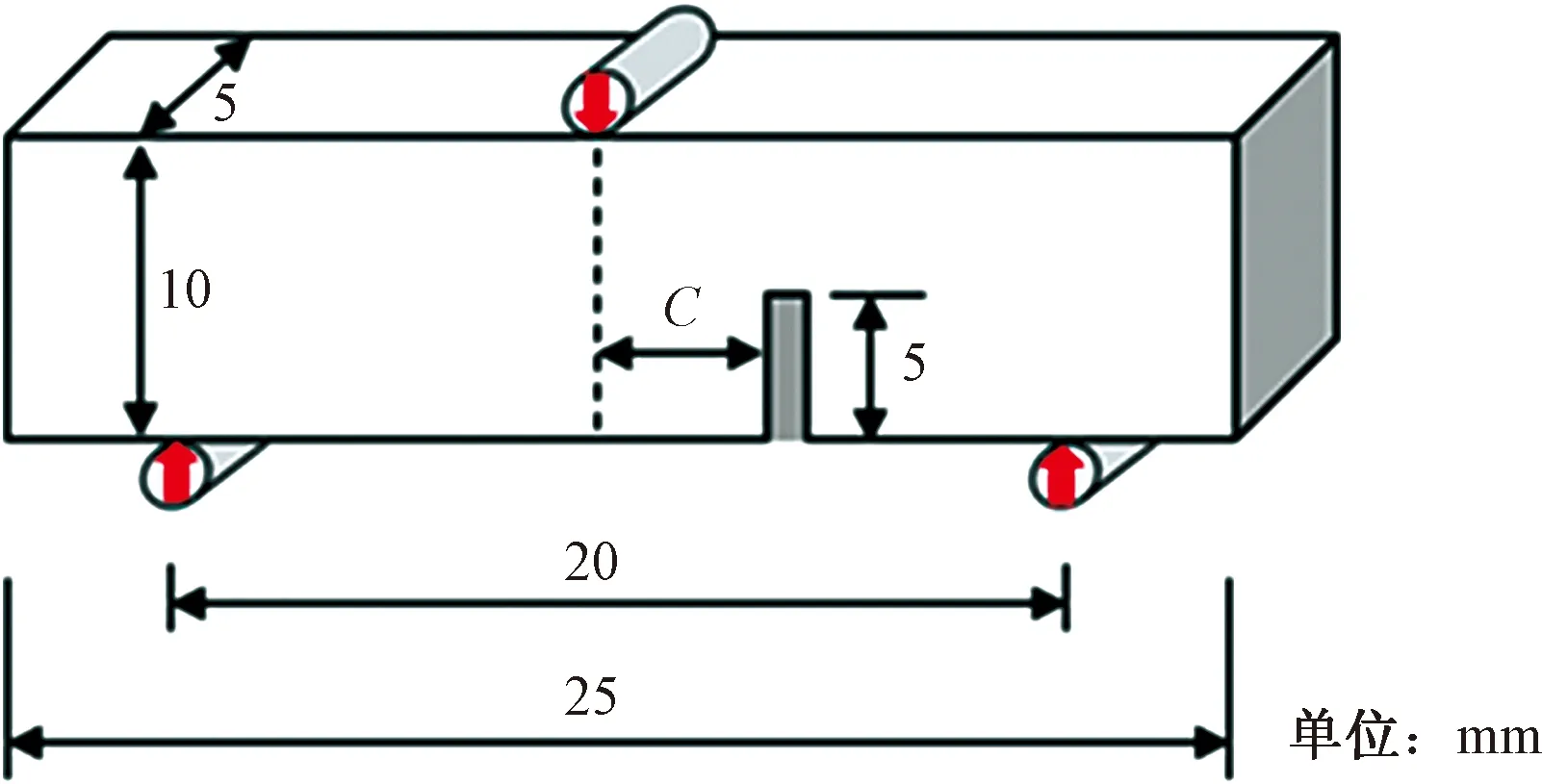
图10 结构几何尺寸及边界条件Fig.10 Geometry and boundary conditions of tested structure

图11 均质模型及裂纹路径Fig.11 Homogeneous model and crack path

图12 结构几何尺寸及边界条件Fig.12 Geometry and boundary conditions of tested structure

3.3 数值模拟

以缺口偏置距离6 mm为例，采用三节点单元，网格总数36 000个，加密区网格尺寸h≈0.1 mm，根据3.3.2节已述，长度参数lc=0.2 mm。采用控制位移方式进行均匀加载，总位移加载分600步完成，均匀位移增量为Δu=0.000 1 mm，总位移u=0.06 mm完成整个裂纹扩展过程。参数临界能量释放率gc是相场法关键参数[24]，很难直接从试验测量，本文研究中选取偏置缺口6 mm室内试验测定的荷载位移曲线进行标定，该室内试验采用控制位移进行加载，加载速率为1×10-4mm/s,详细试验数据参见左建平等[21]。此外，根据左建平等[21, 25]所描述，裂纹扩展大多是沿颗粒扩展，且总是基于最小能量方式扩展。因此，假设颗粒能量释放率为基体的2倍，对于两边的次要区域，由于在均质模型中没有发生裂纹，所以假设次要区域的临界能量释放率远远大于主要区域的临界能量释放率，这样可以让裂纹更好地在基质中扩展。通过室内试验数据标定(图13)，最终确定基体临界能量释放率gc为48×10-5kN/mm，即复合颗粒临界能量释放率gc=96×10-5kN/mm。

采用上述模型参数模拟了偏置距离为1、3、4 mm的三点弯试验，并与上述室内试验中相对应模型实验数据进行对比，如图14所示，本文数值模拟结果与岩石三点弯实验的力与位移曲线拟合较好，对岩石的强度和峰后脆性破坏有较好的预测。因实验中岩石岩样存在初始裂纹，导致实验曲线弹性阶段具有一段压密阶段，需进一步考虑岩石压密阶段，但关键点弹性模量、峰值强度基本吻合。未达到破坏荷载前，力与位移曲线呈线性关系，达到破坏荷载后，曲线开始跌落，直至试样失效，曲线揭示岩石破坏过程为弹脆性破坏过程。从图15看出数值模拟中的峰值强度变化趋势与实验数据一致，随着偏置缺口距离的增加，岩石的破坏荷载也逐渐增加。

图13 能量释放率的标定Fig.13 Calibration of the parameter

图14 力与位移曲线与其试验结果对比Fig.14 Contrast force and displacement curves with experiments

图15 峰值荷载与偏置距离关系Fig.15 Relationship between peak load and bias distance

图16 偏置6 mm时裂纹扩展Fig.16 Crack propagation for the 6 mm offset case

3.4 裂纹扩展的影响因素分析

以缺口偏置距离6 mm岩样的裂纹扩展数值模拟为例，裂纹扩展的整个过程可分为4个阶段，如图16所示：①当位移u=0.037 mm时，缺口开始出现损伤；②位移增加到位移u=0.040 mm时，缺口处的损伤加深，裂纹萌生；③当位移u=0.047 mm时，裂纹开始向顶部快速扩展；④直至位移u=0.06 mm时裂纹扩展至整个岩样，导致岩样失效。裂纹扩展过程与图13的力-位移曲线各个阶段基本一致，但是，从细观尺度而言，岩石中的颗粒大小、位置分布以及物理力学性质都会影响到岩石中裂纹的扩展行为。为此，本节将从细观尺度详细分析裂纹扩展的影响因素。

3.4.1 矿物颗粒分布的影响分析

岩样中的矿物颗粒是随机分布的，为了进一步研究矿物颗粒不同分布对裂纹扩展的影响规律，在矿物组分体积分数一定，排除矿物颗粒尺寸过大过小而引起的离散性，建立了矿物颗粒尺寸一致的3种随机分布模型，裂纹扩展路径如图17所示。模拟结果可以明显看出，受矿物颗粒分布随机性的影响，3个岩样模型的裂纹扩展路径各有不同，但大方向仍是从缺口处萌生，向顶部扩展。力与位移曲线如图18所示，3条曲线在弹性阶段完全吻合，从裂缝萌生开始出现不同，裂缝萌生的起始位置和后期扩展过程均表现出一定的差异，但相差不大。因此，在矿物组分比例一定，颗粒尺寸一致的情况下，颗粒的分布会改变裂纹扩展路径而对力-位移曲线仅有较小影响。

图17 3个不同模型下裂纹路径：相同的颗粒体积分数及大小，不同颗粒位置Fig.17 Three models of different crack paths: same particle volume fraction and size, different particle location

图18 不同模型的力与位移曲线Fig.18 Force and displacement curves of different models

3.4.2 能量释放率的影响分析

岩石中矿物的力学性质，尤其是临界能量释放率的不同也会影响到岩石中裂纹的扩展规律。为深入分析能量释放率的影响规律，研究以下两种情况，A：基质能量释放率小于颗粒能量释放率；B：基质能量释放率大于颗粒能量释放率。

图19 不同gc下u=6 mm裂纹路径图Fig.19 Path of crack u=6 mm under different gc

图20 不同能量释放率的力与位移曲线Fig.20 Force and displacement curves of different energy release rates

针对第一种情况，在主要区域中基质选取4个不同的能量释放率，A1:gc=48×10-5kN/mm；A2：gc=38×10-5kN/mm；A3：gc=28×10-5kN/mm，A4：gc=18×10-5kN/mm，颗粒能量释放率保持gc=98×10-5kN/mm不变，以偏置距离2 mm模型为例，最终裂纹形态如图19所示。为更好地研究裂纹扩展路径的规律，显现出部分颗粒。可以看出，裂纹增长时均绕过矿物颗粒在基质中扩展，与实验观察到的沿晶扩展一致。此外，可以观察到，由于4种基质的能量释放率不同，裂纹在基质中的扩展形态也各有差异，影响了裂纹的最终形态。Zhou等[26]研究表明，均质模型中能量释放率不会改变裂纹的最终形态，而本文在考虑了矿物颗粒后，裂纹路径在不同能量释放率时最终形态发生改变，意味着裂纹扩展行为受岩石内部细观结构影响。图20所示的4种情况下的力与位移曲线趋势几乎一致，不同能量释放率下曲线斜率相同，峰值随gc的增加而增加。

针对第二种情况，保持基质能量释放率gc=48×10-5kN/mm不变，选取两种不同的颗粒能量释放率，B1：gc=48×10-5kN/mm，B2：gc=8×10-5kN/mm。同样以偏置距2 mm模型为例，最终裂纹形态如图21所示。结果表明，随着颗粒能量释放率的降低，裂纹扩展路径逐渐向颗粒内扩展，不再沿颗粒边界在基质中扩展，而出现穿晶扩展。可见，裂纹扩展路径总是趋于最小耗能形式。岩石中矿物颗粒能量释放率的不同会影响裂纹扩展的速度、最大荷载以及裂纹的形态。