考虑多维特征和数据增强的空间负荷预测方法

黄冬梅， 张宁宁， 胡安铎*， 孙园， 孙锦中， 陈岸青

(1.上海电力大学电子与信息工程学院， 上海 201306； 2.上海电力大学数理学院， 上海 201306；3.国网信通亿力科技有限责任公司， 福州 350001)

空间负荷预测(space load forecasting，SLF)可以预测某区域未来负荷的位置和大小。根据SLF的结果来确定供电设备应当配置的容量及其最佳位置，可提高电力系统建设的经济性、高效性、可靠性[1-3]。因此空间负荷预测研究对国民生活的影响越来越大。

区域电力负荷的大小受到社会经济发展状况和气候等多种因素的影响，相对于短期时间负荷预测，空间负荷预测的总体精度不高。文献[4]提出了一种基于分区分类的空间负荷预测方法，考虑了不同时间的气象类型因素。文献[5]主要是考虑到气候变化导致气温升高来预测洛杉矶的峰值电力需求。文献[6]考虑了秩次集对分析理论在处理系统不确定性方面的优势，提出一种新的空间负荷预测方法。文献[7]提出了一种基于元胞负荷特性分析的径向基函数(radial basis function，RBF)神经网络空间负荷预测方法，构建出了一种峰值时段最大负荷数据群(maximum load data group，MLDG)的双向选取模型。文献[8]提出一种GAN生成数据和循环卷积生成式对抗网络(recurrent convolutional generative adversarial networks，RCGAN)预测的空间负荷预测方法。上述文献提出的方法未综合考虑经济发展情况、人口水平、气候条件、产业结构等对负荷变化的影响因素。

空间负荷预测面临的另外一个问题是历史数据匮乏[9]，因此小样本条件下生成数据来扩充样本量是其重要解决方案。文献[10]提出一种基于条件深度卷积生成对抗网络的新能源发电场景数据迁移方法，解决了历史数据缺失情况下生成方法精度较低甚至失效的问题。文献[11]提出了一种用GAN重建地磁数据的方法，解决了大量数据缺失导致重建方法精度不高的问题。文献[12]提出了一种基于生成对抗网络的缺失值填充方法，解决了传统方法难以处理的时序数据历史隐含规律及样本不完整的问题。文献[13]基于深度生成性对抗网络的海杂波数据生成方法进行了数据增强，生成的海杂波数据与真实数据分布类似。由此可见，通过GAN能够保持多种特征变量与负荷之间的映射关系，从而实现样本量的扩充。

针对空间负荷预测的影响因素多样及数据量不足的问题，现提出一种考虑多维特征和数据增强的空间负荷预测方法。该方法首先建立地区多维度特征模型，从不同维度选取了影响电力负荷的因素。然后再利用GAN进行无监督训练，生成足够的新数据增强样本的数据量。最后选择PSO-BP神经网络训练样本搭建预测模型，把测试样本放入训练好的模型中实现空间负荷预测。本文方法考虑了影响区域电力负荷的多个维度的特征，同时实现了小样本数据的增强，具有较高空间负荷预测精度。

1 基本原理

本文提出的考虑多维特征和数据增强的空间负荷预测方法的基本原理如图1所示。

z为随机向量；Pz(z)为均匀分布函数图1 基本原理示意图Fig.1 Schematic diagram of basic principle

(1)多维度特征的选取。首先需要对电力负荷特性的主要影响因素进行分析讨论，根据地区的实际情况，考虑影响当地电力负荷的因素，从不同维度建立地区多维度特征模型。电力系统具有庞大性和复杂性的特点，因此能够影响电力负荷的因素有很多，而在实践中，主要的因素有人口密度[14]、人均可支配收入、产业结构、气候条件等。

(2)数据收集。根据有限的资料按年份查找近10年的数据，每条数据包括此地区该年份的多个负荷特征因素和用电量信息，每个地区都划分好数据组成训练样本集和测试样本集。在搜集的数据中会存在资料有限导致一条数据中个别特征值缺失的问题，本文采用其他年份该变量的平均值来补充缺失的数据。

(3)利用GAN进行数据增强。由于划分后的训练集数据较少，在用神经网络[15-16]预测的时候难以达到理想的精度。为解决数据不足的问题，利用GAN建立生成模型以实现样本数据量的扩充。模型中的生成器和判别器采用多层感知器(multi-layer perceptron，MLP)网络结构，通过选取合适的参数使其彼此之间不断优化，以便能够生成可用于空间负荷预测的数据。

(4)采用PSO-BP神经网络预测。将生成的和原始的训练样本一起放入经粒子群算法优化初始权重和阈值后的BP[17]神经网络中进行训练，待训练完成后，再将测试样本放入该模型中完成预测。PSO每个粒子的位置表示BP神经网络当前迭代中权值的集合，粒子的维数由权值的数量和阈值的个数决定，并以神经网络输出误差作为神经网络训练问题的适应度函数，改变粒子的速度也就是更新网络权值，以减少均方误差。

2 多维度特征选取

为了深入探究电力负荷特性及其变化规律和发展趋势，需要对能影响电力负荷特性的主要影响变量进行分析。本文研究在电力负荷影响因素研究现状的基础上，从不同维度建立了地区多维度特征模型。

地区多维度特征模型如图2所示，该模型能够充分利用配电网和城市各地区大量的量测数据，为在数据驱动下通过深度学习进行空间负荷预测奠定了基础。在现有的参考资料下，本文考虑了地区的三个维度属性对空间负荷特征的影响，分别为开发强度、发展水平和气候条件。

本文结合地区的用电构成和《城市用地分类与规划建设用地标准》进行历史数据的相关性分析，三个维度属性选用的典型特征如表1所示，各特征说明具体如下。

开发强度直接影响到一个地区的用电量[18]。例如，人口密度高的地区比人口密度低的地区用电量明显要多；对于人口密度大的地区，其房屋居住面积和工厂面积也会相对较大，相反人口密度小的地区房屋居住面积和工厂面积也会相对较小。本文采用人口密度、房屋居住面积和工厂面积三个特征作为地区开发强度的衡量指标如表1所示。用电量和该地区的整体经济社会发展水平息息相关，人均可支配收入和工业总产值是体现地区发展水平最直观的指标，此外政府的财政收入也体现了该地区的经济发展水平，所以将一般公共预算收入也作为衡量地区发展水平的特征之一。由于近年来暴雨、高温和低温等气象灾害频繁发生，导致了空调和电采暖设备的大量使用，因此气候条件对用电量的影响也逐渐的重要起来。将平均气温、总降水量、极端最高气温和极端最低气温作为描述气候条件的重要特征。

图2 地区多维度特征模型Fig.2 Regional multi-dimensional feature model

表1 地区多维属性特征及描述Table 1 Regional multi-dimensional features and their description

发展水平和气候条件属性的空间分辨率很大，并不能与小地块相对应，难以识别和获取小地块的这些特征数据。因此本文不细分小地块，选择城市的区级地域大小，同时以年为时间单位来收集数据，使得数据格式简单，并且容易实现。

上述所有的指标数据都可以从地区统计年鉴和区域发展数据库中获得。考虑到如果数据年份太过久远，时间跨度大会形成社会发展水平不同，将影响到数据用电量和各特征之间的映射关系，本文按照区级地域只需获取近10年的数据。

3 基于GAN的生成模型

虽然可以获得10年的年度统计特征数据，但是对于以数据驱动[19]的神经网络方面而言，仍然存在数据匮乏的问题。本文利用GAN来训练样本，学习各特征与用电量的非线性规律，并产生新的样本数据，以此来提高样本的数量。

3.1 数据预处理

由于数据的量纲或者取值大小不一样，因此在进行数据生成之前需要对每条数据做归一化处理。数据归一化处理是指将数据按比例缩放，使其缩放到一个小的特定区间；它是数据挖掘的基础性工作和重要的数据预处理过程，旨在消除各指标间尺度和量纲影响。鉴于需要将这些数据放入GAN模型中进行训练，采用Min-Max归一化方法，其公式为

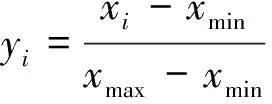
(1)

式(1)中：yi为原始值xi归一化后的值；xmin和xmax分别为所有数据中各特征的最小值和最大值。

3.2 GAN的生成模型

首先需要将原始的训练集设为x，并将训练集中的各条数据之间存在着某种复杂的关系设为Px(x)[8]。整个网络模型中，产生的随机向量z作为模型输入，且服从于均匀分布Pz(z)。G(z,δG)为生成器的输出，D(z,δD)为判别器的输出，δG与δD分别表示各自的网络权重。在深度神经网络中建立反映Pz(x)与Px(x)的映射关系，然后就可以通过GAN模型进行训练，生成满足原数据用电量与多特征关系的新数据。

模型训练相对复杂，可将其分为两个部分，作用都是交替优化GAN以实现最好的结果。第一阶段，固定判别器更新生成器的网络权重，再通过损失函数优化生成器的参数，从而使判别器的准确率能够降到最低。第二阶段，固定生成器更新判别器的网络权重，再通过损失函数优化判别器的参数，从而使生成器的准确率能够达到最高。生成器将目标函数(2)优化达到最小化：

VG=Ez＾Pz(z)[log2{1-D[G(z)]}]

(2)

式(2)中：VG为生成器的目标函数；Ez＾Pz(z)为Pz(z)的数学期望；D[G(z)]为判别器判别的结果；G(z)为生成器产生的新数据。判别器将目标函数(3)优化达到最大化：

VD=Ex ＾Px(x)[log2D(x)]+

Ez ＾Pz(z)(log2{1-D[G(z)]})

(3)

式(3)中：VD为判别器的目标函数；Ex ＾Px(x)为Px(x)的数学期望；D(x)为真实数据。将两式组合可得到GAN模型训练过程的整个目标函数为

Ez ＾Pz(z)(log2{1-D[G(z)]})

(4)

式(3)中：V(G,D)为GAN的目标函数。

GAN模型中的生成器和判别器均采用MLP网络结构，损失函数为二分类交叉熵函数。生成器和判别器均采用LeakyReLU函数作为激活函数，可以解决训练过程中会出现神经饱和的问题，提高计算效率。

采用Adam优化器进行更新优化GAN模型中两部分的网络参数。通过利用优化网络参数后的判别器进行多次无监督训练生成器来优化其网络参数，以便生成器能够生成更具真实性的数据，直到判别器判别全部的新生数据为真实数据为止。将生成的数据进行反归一化，最终生成可用于空间负荷预测的新数据，实现最好的数据增强效果，满足实验的可行性。

4 实例分析

4.1 多维度特征数据的收集与处理

以东部某市4个区为例，每个区搜集了2010—2019年的数据，每条数据包含该年用电量和地区多维度的10个特征变量。将2010—2015年的数据划分为训练集的样本，2016—2019年的数据划分为测试集的样本。划分后的训练样本达不到深度学习训练的数量规格和数据多样性要求，因此需要将4个地区的训练样本作为GAN生成模型的原始样本进行数据生成，充分学习和把握用电量和10个特征变量之间的关系和规律，使生成的数据满足丰富历史数据的数量和多样性。4个地区部分数据如表2所示。

4.2 空间负荷预测实例分析

4.2.1 多维度与单维度属性特征预测结果对比

不同维度的特征对负荷的影响程度并不一样，在实验中，预测效果最好的维度属性是开发强度。因此，将不同维度特征综合的预测值与开发强度属性下特征的预测值进行比较，具体如表3所示。

表2 各区2010—2019年部分数据Table 2 Partial data of each district from 2010 to 2019

预测值相对误差区间比例如图3所示。结果表明，考虑多个维度特征的预测结果要与只考虑单个维度特征的预测结果相比，效果要好很多。其中，多维度属性特征的预测结果相对误差在5%以内的达到43.75%，而对应的单维度属性特征预测结果只达到12.5%。因此，考虑多个维度特征的方法具有更高的预测精度。

表3 多维度与单一维度属性特征的空间负荷预测结果Table 3 Spatial load forecasting results based on multi-dimensional and single dimensional attribute characteristics

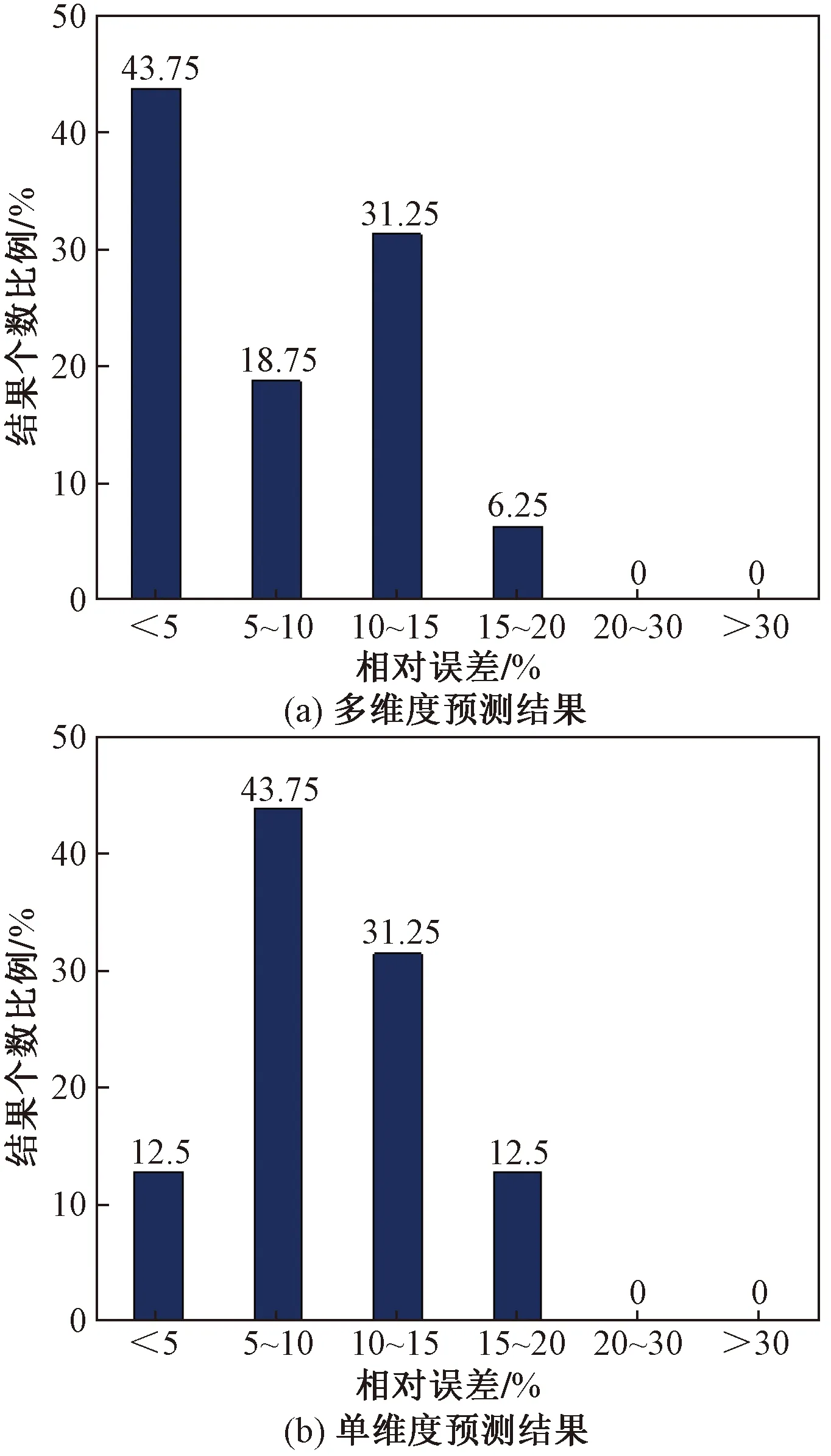
图3 多维度与单一维度属性变量预测结果对比Fig.3 Comparison of results of multi-dimensional and single-dimensional aided prediction

4.2.2 有无数据增强的预测结果对比

考虑每个地区用电量与多特征变量的映射关系会存在差异，为了减少生成数据的平均绝对误差，保证生成的数据具有较高的精度，因此需要每个地区的数据分别单独用GAN模型进行生成数据。经过实验分析，每个地区的数据生成4倍最为合适，把生成后的数据与4个地区的原始训练样本放在一起实际上就实现了样本的数据增强，再将增强后的数据放入PSO-BP网络模型中训练，训练完成后，最后将测试样本放入该模型中进行预测。将预测值与未增强训练样本的预测值进行比较，具体如表4所示。

表4 基于PSO-BP神经网络的空间负荷预测结果Table 4 Spatial load forecasting results based on PSO-BP neural network

图4 有无数据增强预测结果对比Fig.4 Comparison of prediction results with and without data enhancement

预测值相对误差区间比例如图4所示。结果表明，用GAN进行数据增强后预测结果的相对误差远低于未使用GAN数据增强预测结果的相对误差。其中，数据增强的全部预测结果中相对误差均小于20%，相对误差小于5%的比例为75%，相对误差在5%～10%的比例为12.5%，两者之和的比例就达到了87.5%。而未数据增强预测结果对应的比例分别为43.75%和18.75%，两者之和为62.5%。由此可见，用GAN进行数据增强可以大幅提高预测精度。

4.2.3 其他传统方法的预测结果对比

本文所提出的考虑多维特征和数据增强的空间负荷预测方法是否具有有效性，这里将其预测结果与现有的一些预测方法进行比较验证，即传统的3种预测方法：灰色理论法、指数平滑法和线性回归法，以及能够较好处理高维属性性能的最小二乘支持向量机[20-24](least square support vector machine，LS-SVM)方法。不同方法的预测结果如表5所示。

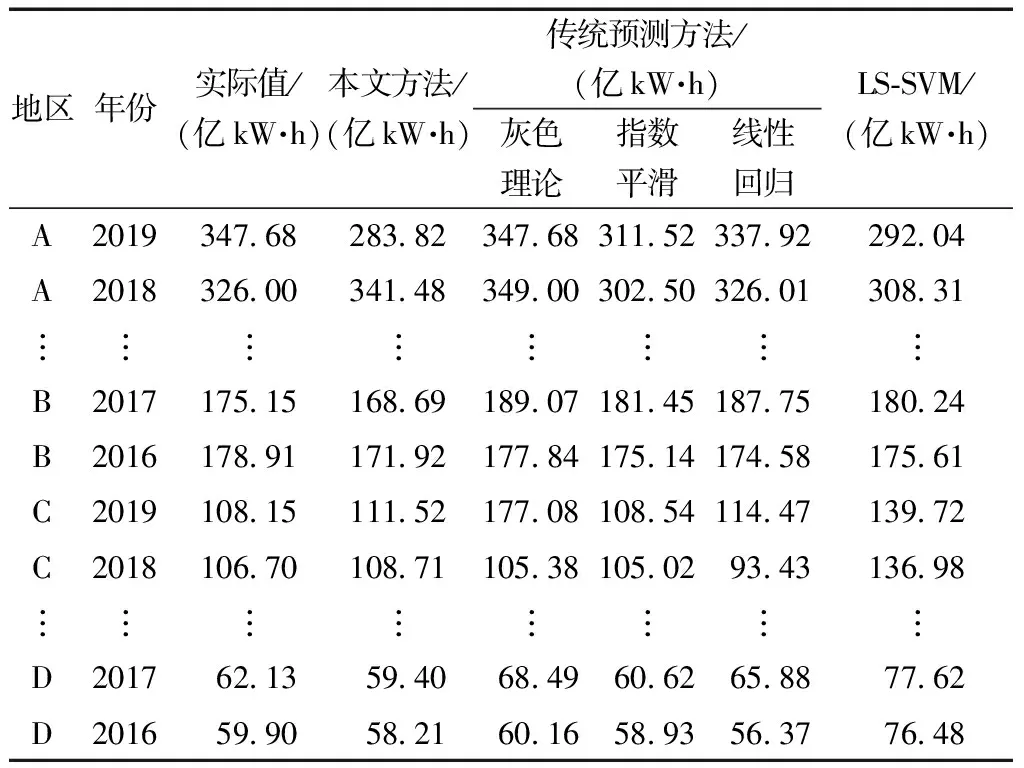
表5 不同方法的空间负荷预测结果Table 5 Spatial load forecasting results of different methods

图5 不同预测方法的相对误差比较Fig.5 Comparison of relative error of different prediction methods

求取各种方法的相对误差百分数，统计各误差区间比例，如图5所示。从表5和图5的结果可以看出：就预测结果整体而言，采用本文方法得到的用电量预测结果，相较于LS-SVM和传统的3种预测方法的预测结果而言，各预测结果的相对误差明显较小，预测精度明显提高；同时本文方法所得到的预测结果在较小的相对误差区间内的个数比例较大，这表明本文方法整体上优于灰色理论法、指数平滑法、线性回归法和LS-SVM的预测方法。因此。与现有的一些传统方法相比，在进行空间负荷预测时本文的方法具有较好的特征提取性能和较高的负荷预测精度。

5 结论

针对空间负荷预测影响因素多样及数据匮乏的问题，提出了一种考虑多维特征和数据增强的空间负荷预测方法。与现有的一些方法相比，该方法具有以下优点。

(1)综合3个维度的主要特征因素来反映与负荷变化的关系，考虑的影响因素更加全面，更符合区域负荷在不同类型因素下受到不同影响的情况。相比于不考虑影响空间负荷影因素或只考虑单种类型因素的方法，其预测精度更高。

(2)本文方法可以学习到用电量与各影响特征之间的映射关系，实现在历史数据匮乏的场景下生成符合原始数据变化规律的新样本，使得用于空间负荷预测的训练样本得到充分、有效的增强，提高了模型的预测精度，为新建成或历史样本不足的待预测区域提供了一种新方法。