高密度等离子体喷流高速对撞的二维辐射流体模拟研究*

杨孟奇 吴福源 陈致博 张翼翔 陈一 张晋川 陈致真 方志凡 Rafael Ramis 张杰

1)(上海交通大学物理与天文学院,激光等离子体教育部重点实验室,上海 200240)

2)(上海交通大学致远学院,上海 200240)

3)(上海交通大学 IFSA 协同创新中心,上海 200240)

4)(西班牙马德里理工大学航空航天学院,马德里 28040)

等离子体喷流对撞是天体物理和激光等离子体物理中常见的流体力学现象.构建对撞等离子体状态和喷流初始条件的流体定标关系,对于相关实验的物理设计和数据分析具有重要意义.本文采用最新升级的二维自由拉格朗日辐射流体模拟程序MULTI-2D,研究了高速(≥100 km/s)、高密度(≥10 g/cm3)条件下的喷流对撞过程.基于不同条件下等离子体喷流高速对撞过程的模拟数据,通过机器学习中的贝叶斯推断方法构建了描述等离子体喷流对撞过程的流体定标规律.研究结果表明:锥形等离子体喷流对撞易于形成等容分布的高密度等离子体;提高喷流的初始密度和速度,有利于提高对撞等离子体的密度和温度;提高喷流的初始温度,有利于提高对撞后的温度,但会降低对撞后的等离子体密度.当等离子体喷流的初始密度、温度和速度分别设定为15 g/cm3,30 eV和300 km/s时,对撞后的等离子体密度可以达到300 g/cm3 以上,这对于双锥对撞点火方案中的快电子加热过程非常重要.

1 引言

等离子体喷流对撞是天体物理和激光等离子体物理常见的流体力学现象.在实验室模拟天体物理过程时,等离子体喷流可以通过激光烧蚀[1−5]或Z 箍缩内爆[6]产生,当两团高度准直的等离子体喷流相向运动时,即可发生对撞过程.激光聚变[7−11]的靶丸内爆可以分为等熵压缩、内爆加速、阻滞约束和点火燃烧4 个过程,其中高密度冷燃料壳层的减速阻滞过程也可采用对撞过程描述.例如,美国利弗莫尔国家实验室的Hurricane等[11]采用一维平板对撞模型,研究了等压点火模型中热斑参数和冷燃料壳层初始状态的流体定标规律,为分析内爆不对称性对激光聚变实验结果的影响提供了有力支撑.因此,研究等离子体喷流的对撞过程对于深入理解天体物理中的物理规律和解决人类清洁能源发展的惯性聚变研究均有重要意义.

在过去几十年里,国内外的学者们深入研究了准直喷流的形成和传播过程.例如,Albertazzi等[1]通过轴向磁场准直激光烧蚀平面靶产生的低密度等离子体,产生了和原初恒星体(YSO)喷流类似的等离子体喷流.Li等[2]通过激光辐照V 形靶研究了准直等离子体喷流的对撞过程,揭示了自生磁场随喷流运动的机理.裴晓星等[4]采用“神光II”装置的八路激光辐照铝平面靶,通过重联电场产生和W43A 恒星喷流类似的双极等离子体喷流.Lebedev等[6]通过Z 箍缩锥形丝阵产生了辐射冷却的等离子体喷流,并且初步研究了等离子体喷流和静止物体碰撞产生X 射线的过程.但是,受限于研究人员的研究兴趣和激光装置驱动能量等原因,上述实验产生的等离子体喷流密度普遍较小(<10 g/cm3),对高密度条件下的等离子体喷流对撞过程研究得较少.

高密度等离子体喷流的高速对撞涉及到物质的压缩和加速过程,球形内爆是实现物质高倍率压缩和超短距离加速的有效途径之一[12].双锥对撞点火方案将球形内爆中两个相向运动的锥形内爆分离出来,能够在规模相对较小的驱动激光装置上,实现锥内球冠靶内爆等离子体喷流的高速对撞[13−15],一方面可以为随后的快电子束流加热实现核聚变而创造条件,另一方面可以为研究高密度等离子体喷流的高速对撞提供良好的实验平台.本文采用二维辐射流体模拟程序MULTI-2D,研究双锥对撞点火构型中高密度等离子体喷流高速对撞的流体动力学过程,并给出反映对撞等离子体状态和喷流初始条件因果关系的流体定标规律.

本文介绍了MULTI-2D 程序的计算模型,分析了锥形等离子体喷流的对撞流体动力学过程,并展示采用机器学习算法获得的流体定标规律.

2 计算模型

MULTI 程序是西班牙马德里理工大学Ramis等[16−19]开发的系列开源辐射流体力学程序,已广泛应用于激光聚变[20]、Z 箍缩聚变[21−23]和重离子聚变[24]研究.其中MULTI-2D 程序采R94和C 语言混合编写[16],最新升级的版本可在二维非结构网格求解多层、多介质、多物理问题,并且具备二阶精度的自由拉格朗日变量重映功能.状态方程和不透明度参数分别由MPQEOS 程序[25]和SNOP 程序[26]生成,调用时采用列表插值的形式.MPQEOS程序采用修正后的托马斯-费米模型描述给定密度和内能所对应的物态参数[25,27],使得高密度低温情况下的量子简并效应能够得到正确描述.MULTI-2D 程序使用交错网格定义变量,密度、压强、磁感应强度定义在网格中心,速度、温度和内能定义在网格节点.本文采用最新升级的MULTI-2D 程序进行等离子体喷流的对撞过程模拟.MULTI-2D 程序采用的辐射磁流体力学方程组如下:

方程(1)—(5)分别为质量守恒方程、动量守恒方程、能量守恒方程、磁场演化方程和辐射输运方程.其中ρ是密度,m是质量,V是体积,u是速度,P是物质压强,Pv是人工黏性压强,J是电流密度,B是磁感应强度,e是单位质量的等离子体内能,qe是电子热流,qv是人工热流,Sex是外部源项(如激光和X 射线能量沉积),η是电阻率,µ0是真空磁导率.I是频率积分角度分辨的辐射强度,n是辐射传播方向上的单位向量,IP是普朗克强度,λ是辐射平均自由程.

方程(2)中人工黏性压强Pv的作用在于捕捉流场中的冲击波,其采用冯诺依曼等给出的计算方法确定[28].方程(3)中人工热流qv的作用在于消除冲击波附近的过分加热现象,其采用Noh[29]和王瑞利[30]等人给出的计算方法确定.Noh[29]指出,对于采用人工黏性处理冲击波的流体程序,如果计算中存在强冲击波在固壁边界反射等特殊情况时,冲击波附近存在过热现象是必然的,采用人工热流可以在保证系统总能量守恒的条件下有效消除冲击波附近的过热现象.更多有关MULTI-2D 程序物理模型和求解算法的信息可以参见文献[17,18].

3 锥形等离子体喷流对撞

图1 所示为汇聚几何条件下锥形等离子体喷流对撞的密度和温度演化过程.为了使获得的计算结果对激光聚变实验更有参考意义,采用双锥对撞点火方案中的典型等离子体条件作为对撞初始条件.根据对称性分析,计算区域设置为整个对撞区域的1/4,即图1 显示区域的右上角区域.半径和高度方向的计算区域均为0 到400 µm,网格大小为200× 200.金锥的开口投影角为100°,金锥的密度为19.2 g/cm3,温度为0.001 eV,厚度为28 µm,下锥口距赤道平面60 µm.金锥内的DT 等离子体喷流分布在R=100 µm到R=200 µm 之间,密度为15 g/cm3,温度为30 eV,速度为300 km/s.金锥内的其余区域为CH 背景等离子体,密度为0.01 g/cm3,温度1000 eV,速度为零.金锥外的其余区域为DT 背景等离子体区域,密度为0.01 g/cm3,温度为1 eV,速度为零.计算区域的左边界和下边界采用反射边界条件,其他边界采用出流边界条件.按等温声速估算[31],温度为30 eV的氘氚等离子体声速约为50 km/s,只要喷流速度大于200 km/s,相应的马赫数就会远大1.马赫数是等离子体喷流速度和声速的比值(M a=V/Cs),马赫数的平方正比于等离子体喷流动能和内能的比值(Ma2∼马赫数远大于1,说明此时的等离子体喷流具有很强的可压缩性.

图1 不同时刻锥形等离子体喷流对撞的密度和温度分布图Fig.1.Density and temperature distributions of conical plasma jets at different times during the collision.

由图1 可知,等离子体喷流的密度在球形汇聚过程中发生了显著提高.例如,在等离子体喷流开始剧烈对撞前,等离子体的峰值密度已经因为球形汇聚效应在0.25 ns 时从初始的15 g/cm3提高到了40 g/cm3以上.球形汇聚效应带来的密度提升可以用运动粒子与金锥壁相互作用获得速度分量的观点进行部分解释:如果将等离子体的径向运动速度在直角坐标中分解为横向速度和纵向速度,纵向速度使等离子体喷流越来越靠近对撞中心;而横向速度由于金锥壁的存在,沿着Y轴旋转对称,大小相等,方向指向Y轴,使等离子体越来越靠近Y轴,起到横向压缩作用,从而使得等离子体喷流密度在球形汇聚过程中不断提升.

从图1中t=0.45 ns 时刻的温度分布可以看到向外传播的高温弓形激波,这是对撞产生的高温高压激波在周围的背景等离子体中传播产生的.由于背景等离子体的密度和压强远低于喷流等离子体的密度和压强,所以对撞产生的冲击波在背景等离子体中的传播速度远大于在喷流等离子体中的传播速度,并且在波前位置具有较高的温度.又因为喷流对撞持续产生着横向逃逸的等离子体,所以对撞产生的冲击波在背景等离子体传播过程表现为弓形激波.

图2 给出了球形汇聚条件下的等离子体喷流运动与对撞过程中的状态在温度-密度相图上的轨迹,其中密度取每个时刻的最大密度,温度取最大密度所在位置对应的温度.由图2和图1 可知,球形汇聚等离子体在对撞前的大部分滑行过程是无冲击波的,等离子体的温度上升轨迹和费米温度代表的等熵压缩直线几乎完全平行.在对撞产生的反射冲击波作用下,由于等离子体喷流的动能转换为内能,对撞等离子体的温度急剧上升.0.25 ns时,对撞中心附近的等离子体峰值温度可以达到1 keV;0.45 ns时,等离子体的峰值密度可以达到300 g/cm3,并且在|X|<15 µm且|Y|<25 µm的区域(图1黑色圆圈内)具有近似均匀的等容分布结构,此时的等离子体峰值温度约为468 eV.根据Tabak等[9]的研究结果,300 g/cm3的等容分布等离子体需要的快点火皮秒激光能量和强度分别约为18 kJ和6.8×1019W/cm2,有利于降低快点火方案对皮秒激光的技术要求.

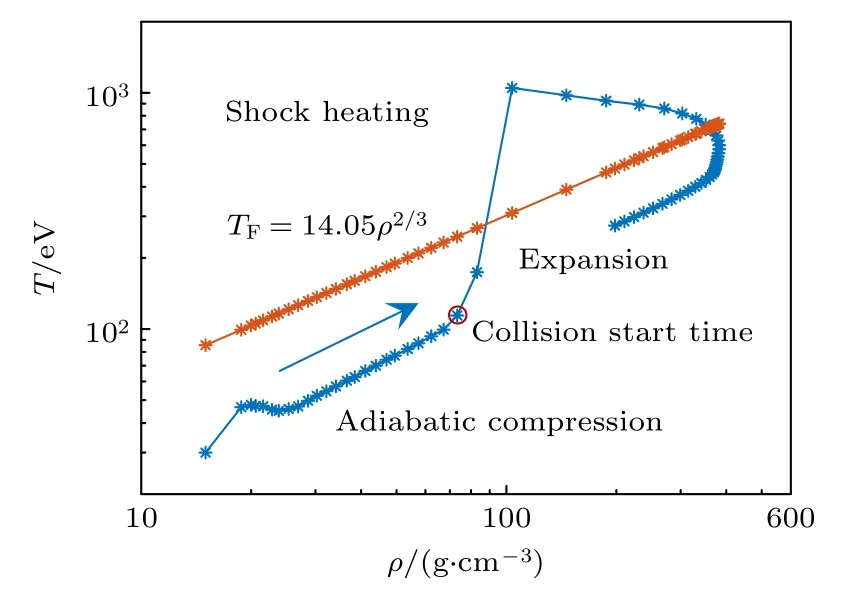
图2 锥形喷流对撞过程中的等离子体状态在温度-密度相图上的运动轨迹,箭头表示时间的增大方向,橙色直线表示不同密度对应的费米温度Fig.2.The trajectory of the plasma jet on the temperaturedensity phase diagram during the collision,the arrow in the Fig.indicates the increasing direction of time,and the orange line indicates the Fermi temperature at different densities.

图3 给出了对撞过程中快点火方向面密度(图1中X方向)、峰值压强和对撞区归一化X 射线辐射功率随时间的变化曲线.由图3 可知,快点火方向的峰值面密度可以达到1.5 g/cm2,压强可以达到200 Gbar(1 bar=0.1 MPa).X 射线功率的峰值时刻和压强的峰值时刻几乎相同,压强的峰值时刻(0.32 ns)比面密度的峰值时刻(0.48 ns)早160 ps,原因是压强的大小同时决定于温度和密度,而对撞产生的高温等离子体会因为电子热传导、X 射线韧致辐射和向外膨胀逐渐冷却.由该图还可知,对撞获得的高密度等离子体可以依靠惯性约束维持200 ps 左右(0.38—0.58 ns),这为进一步提升物质能量密度的快电子点火提供了有利的时间窗口.在实验中,等离子体喷流对撞加热与密度快速提升形成的X 射线功率峰可以采用X 射线闪烁体功率计或者X 射线条纹相机测量,为时间分辨的等离子体面密度测量提供参考.

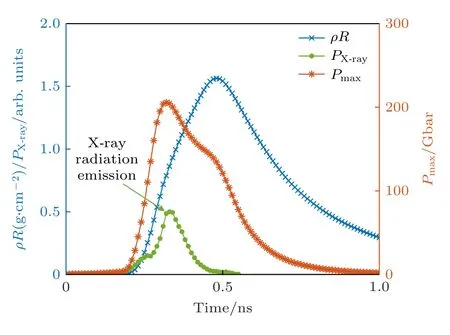
图3 对撞过程中快点火方向面密度、峰值压强和对撞区归一化X 射线辐射功率随时间变化曲线Fig.3.Time evolution of areal density,peak pressure in fast ignition direction and normalized X-ray radiation emission power in collision area.

4 锥形喷流对撞的流体定标关系

为了获得不同初始条件下的等离子体喷流对撞规律,利用控制变量法对密度ρ0、速度V0和温度T0等初始等离子体参数进行了扫描分析.参数扫描的采样方法是:密度范围10—50 g/cm3,每5 g/cm3取一个点;速度范围100—500 km/s,每50 km/s 取一个点;温度范围10—100 eV,每10 eV取一个点;总共计算810 个采样点.这些参数范围代表了当今实验室天体物理和激光聚变实验可以获得的典型等离子体喷流初始状态.图4 所示为喷流初始条件变化时,对撞等离子体的密度、温度和压强的变化曲线,其中对撞后的密度取的是对撞过程的最大密度,温度和压强取的是密度最大值时对应的数值.该图的绘制方法是以第3 节的喷流初始状态(ρ0=15 g/cm3,V0=300 km/s,T0=30 eV)为基点,每次扫描其中一个变量,同时保持其他两个变量的大小不变.例如研究不同初始密度的影响时,喷流的初始速度和初始温度始终保持为V0=300 km/s和T0=30 eV 不变.

图4 对撞等离子体参数随喷流初始条件的变化曲线(a)V0=300 km/s,T0=30 keV;(b) ρ0=15 g/cm3,T0=30 keV;(c)ρ0=15 g/cm3,V0=300 km/sFig.4.Variations of colliding plasma parameters with the initial conditions of plasma jets:(a)V0=300 km/s,T0=30 keV;(b) ρ0=15 g/cm3,T0=30 keV;(c)ρ0=15 g/cm3,V0=300 km/s.

由图4 可以观察到如下几个规律:1)喷流的初始密度越高,对撞后的等离子体密度和压强也越高,但对撞等离子体的温度变化较小;2)喷流的初始速度越大,对撞后获得的峰值密度、温度和压强越大;3)喷流的初始温度越高,获得的对撞等离子体温度越高,获得的峰值密度和压强越低.后文将在构建流体定标关系时进一步印证上述规律,并且从等离子体喷流的初始马赫数、动理压强和等熵参数方面进行一定的解释.

量子简并是高密度等离子体喷流和白矮星等致密天体具有的一种特殊现象[32,33].量子简并等离子体具有和理想气体不一样的状态方程和热力学性质.由于泡利不相容原理,量子简并效应会产生电子简并压强,对应于等离子体在费米温度下的压强.费米温度是判断等离子体是否处于量子简并状态的常用标准之一.根据Atzeni等[31]给出的公式,DT燃料的费米温度可以表示为TF=TF(ρ)=14.05ρ2/3,密度为15 g/cm3的DT等离子体的费米简并温度约为85 eV,即本文模拟的喷流初始状态大部分处于量子简并状态.

图5 给出了喷流初始密度为15 g/cm3时,不同初始温度和初始速度获得的对撞等离子体状态,以及费米温度随密度的变化曲线TF(ρ).由图5 可知,对于同一个速度系列,随着喷流初始温度增大,对撞后的等离子体状态逐渐从右下角的量子简并区域进入左上角的非量子简并区域.喷流初始温度相同时,随着喷流初始速度提高,对撞后的等离子体温度和密度都会提高,但喷流速度大于300 km/s时,温度的提升效应更显著,对撞后的等离子体更容易进入非简并状态.由该图还可知,如果想在初始密度15 g/cm3的条件下获得密度接近200 g/cm3的非量子简并等离子体,那么喷流的速度至少需要达到200 km/s.相反,如果想在初始密度15 g/cm3的条件下获得密度超过200 g/cm3的简并等离子体,则喷流的初始温度需要控制在30 eV 以下,这需要在喷流形成的过程中仔细调控冲击波的时序和强度,以控制喷流形成过程的熵增.

图5 喷流初始密度为15 g/cm3时,不同初始温度和初始速度获得的对撞等离子体状态,橙线表示费米温度随密度的变化曲线,箭头表示喷流初始速度相同时,喷流初始温度的增大方向Fig.5.Colliding plasma states obtained at different initial temperatures and velocities when the initial jet density is 15 g/cm3,the orange line in the figure represents the variation curve of Fermi temperature with density,and the arrow represents the increasing direction of the initial temperature when the initial velocity is the same.

等离子体喷流对撞过程的物理规律可以采用机器学习算法抽象为替代模型(surrogate model)或者流体定标关系.例如,采用模拟数据训练人工神经网络或随机森林模型,可以获得具有较强预测能力的流体程序替代模型.但是这种依赖于计算机的替代模型本身是一个黑匣子,不利于解释自变量和因变量之间的因果关系.为了直观地揭示等离子体喷流对撞前后的因果关系,在解析推导和实验现场等脱离计算机的环境提供有效的理论参考,采用机器学习中的贝叶斯推断方法[34]构建了幂律形式的流体定标关系.这种基于概率编程的贝叶斯推断方法,不仅具有传统最小二乘法具备的参数估计功能,而且具备给出相关参数的概率分布等其他潜在优势.罗彻斯特大学的Betti 团队[35]曾经借助该方法对激光聚变实验进行了优化设计,在OMEGA装置后续的实验中实现了中子产额的3 倍提升.

图6 所示为采用贝叶斯马尔可夫链推断得到的等离子体喷流峰值密度流体定标关系.拟合关系中的数字表示贝叶斯推断得到的参数平均值,ϵstd表示每个参数对应的标准差,对角线表示拟合值和模拟值完全一致时的参考线.由该图可知,几乎所有的数据都分布在参考线附近,每个参数对应的标准差都远小于平均值.这说明基于贝叶斯推断得到的流体定标关系可以很好地反映模拟数据背后隐含的流体规律.此外,每个参数都存在一定的概率分布,而不是一个单点数值,说明获得的流体定标关系在某一个参数范围内都成立,具有一定的健壮性.

图6 (a)贝叶斯推断得到的对撞密度定标关系,橙色直线表示拟合数据和模拟数据完全一致时的参考线;(b)相关参数的归一化概率分布灰色直线表示每个参数归一化概率分布对应的平均值位置Fig.6.(a)The calibration relationship of plasma density,the orange line represents the reference line when the fitting data is completely consistent with the simulation data;(b)the normalized probability distribution of relevant parameters inferred by Bayes,the gray line represents the average position corresponding to the normalized probability distribution of each parameter.

表1 总结了对撞等离子体参数随喷流初始条件变化的流体定标关系,其中ρ0,V0和T0分别表示对撞前的等离子体喷流密度(g/cm3)、速度(km/s)和温度(eV).由表1 可知,提高喷流的初始密度和初始速度,有利于提高表格中所有的对撞等离子体参数.这是因为初始密度和初始速度越大,喷流的马赫数(M a=V0/Cs)和动理压强越大,喷流的可压缩性越强,对撞越剧烈,阻滞时刻获得的温度、密度和压强也越大.提高喷流的初始温度,一方面有利于获得较高的对撞等离子体温度,另一方面却不利于获得较高的对撞等离子体密度、面密度和压强.这是因为温度较高的喷流具有较低的马赫数、较高的等熵参数和较大的等温声速,等离子体的可压缩性较小,同时使密度降低的稀疏波影响较显著.如果用理想气体模型估算,等熵参数可以表示为∝T,即等离子体的等熵参数和温度成正比.对撞后的等离子体密度与喷流初始速度成近似正比是汇聚几何中等离子体喷流对撞的显著特点,指明了一条获得极端高密度物质的有效途径.对撞压强(能量密度)和对撞速度近似呈平方关系,则说明在追求高能量密度的激光聚变中,应该追求足够大的内爆速度.

表1 对撞等离子体参数和喷流初始条件的流体力学定标关系Table 1.Scaling laws between colliding plasma parameters and the initial conditions of plasma jets.

需要指出的是,由于对撞条件和物理机制两方面的限制,本数据库中包含了非简并(T>TF)和弱简并(0.3TFTF),得到的归一化电子压强和归一化温度近似成正比,即Pe/PF=2.45T/TF;对于弱简并状态(0.3TF

图7 对撞后的氘氚等离子体状态在压强-温度相图的分布Fig.7.The DT plasma states after collision in pressuretemperature phase diagram.

根据表1 给出的流体定标关系和脱简并条件(T >TF),还可以得出氘氚等离子体喷流对撞产生非简并等离子体的判据,具体如下式所示:

由该表达式可知,在给定双锥对撞点火所需的密度时,为了获得非简并的等离子体,有必要精确调控压缩激光的功率波形,使得等离子体喷流在对撞前具有足够高的速度和温度.但是如果想要产生致密天体所存在的量子简并等离子体,则需要严格控制等离子体压缩过程的熵增,使得等离子体喷流在对撞前具有较高的密度和较低的温度.

5 总结与讨论

本文采用最新升级的二维自由拉格朗日程序MULTI-2D,研究了球形汇聚条件下的高密度双锥等离子体喷流的高速对撞过程.数值模拟结果表明,具有开放边界的等离子体喷流对撞易于形成等容分布的对撞等离子体结构.球形汇聚效应能够极大地提高对撞获得的等离子体密度、面密度和压强.基于贝叶斯推断获得的流体定标关系表明:提高喷流的初始速度,能够提高对撞等离子体的密度和温度;提高喷流的初始温度,可以提高对撞后的等离子体温度,但会降低对撞后的等离子体密度.因此,对于希望在对撞后形成超高密度量子简并等离子体的物理目标,建议在提高对撞速度的同时严格控制喷流形成过程的熵增,以获得较低的初始喷流温度;对于需要在对撞后形成非简并等离子体的物理目标,建议在控制流体不稳定性发展的前提下尽可能提高内爆动能,同时适当提高内爆过程的燃料熵增.

需要说明的是,本文的模拟计算没有考虑流体不稳定性、内爆不对称性和不同对撞汇聚比等因素带来的影响.考虑这些因素时,获得的流体定标关系中的数值将会有所不同,但是不会改变本文的主要结论,如双锥喷流对撞容易形成等容分布结构以及对撞等离子体参数与等离子体喷流初始参数的关系等.如果考虑流体不稳定性,对撞获得的等离子体密度将会有所下降.但是因为锥形喷流在对撞过程没有内部低密度、高压强气体的阻滞作用,喷流内界面的瑞利泰勒不稳定性发展将不显著或者不存在,瑞利泰勒不稳定性对等离子体对撞结果的降低作用可能比较小.对于等离子体喷流的内爆不对称性,实验上可以通过制靶工艺和激光波形调控加以控制,使得内爆不对称性的影响降到可以接受的水平.在将来的研究中,将把流体不稳定性和内爆不对称性等非理想因素逐步纳入模拟计算,以获得更精确的模拟结果,并在双锥对撞点火方案下一步的实验设计中发挥更大的所用.