基于机器学习的橡胶改性再生骨料混凝土抗压强度预测研究
2022-12-04陈双庆
陈 林 ,陈双庆
(1.中交第二航务工程局有限公司,湖北 武汉 430000;2.湖南文理学院,湖南 常德 415000;3. 中南大学 土木工程学院,湖南 长沙 410014)
1 概述
建筑固废的数量逐年上升,据估计,中国每年约有36亿kg的轮胎直接丢弃于垃圾填埋场[1],这不仅浪费了空间,而且严重污染了环境。为了解决上述问题,研究发现在再生骨料混合物中加入橡胶颗粒可提高再生骨料混凝土的高温压缩性能,称为橡胶改性再生骨料混凝土(RRAC),不仅提高建筑固废的利用率,还降低建筑固废对环境的污染。
由于再生骨料混凝土表面被旧砂浆覆盖,使得再生骨料混凝土界面过渡区强度显著减弱。除此之外,与天然骨料混凝土相比,再生骨料混凝土孔隙率更高,内部微裂纹更多,力学性能差异显著[2]。根据ALEXANDRIOU[3]等的研究结果,当RA替换率为75%时,抗压强度下降高达26%。但这种负面影响可以通过一些RA处理方法来消除,如球磨机法。
混凝土结构容易发生火灾破坏。因此,结构在高温下的性能必须按照相关标准予以考虑。SARHAT[4]等证明了相较于天然骨料,再生骨料的热膨胀系数更接近砂浆,从而降低了热损伤。CHEN[5]等发现当RA替换率小于50%时,再生骨料混凝土的强度损失率降低,强度甚至高于天然骨料混凝土。因此,再生骨料混凝土的热损伤还需要进一步研究。此外,橡胶颗粒(RPs)作为细集料已被许多学者研究[6-7]。有学者证实了RPs的使用能提高混凝土的耐高温性。根据蒸汽压理论[8],RPs在高温下软化分解,导致混凝土中孔隙数量增加,内部蒸汽压降低。由于RPs对混凝土的韧性作用,橡胶改性再生骨料混凝土也被许多学者关注。RRAC的变形能力优于RAC,当RPs的加入可以减少RAC的剥落现象。这是由于较高的温度下,大量的内部气孔有助于内部蒸汽通过逸出的RPs释放。
机器学习(ML)近年来受到广泛关注,数据驱动研究方法已经被广泛应用于建筑行业[9]。然而,少有预测模型用来指导RRAC的热力学性能,而这对研究高温状态下橡胶改性再生骨料混凝土路面抗压性能有重要意义。ML模型可以在不需要显式编程的情况下从数据集中提取有价值信息,并获得可靠准确预测结果。人工神经网络(ANN)、支持向量回归(SVR)和随机森林(RF)是目前流行3种ML模型,在混凝土领域得到了广泛应用。虽然ML模型在解决预测问题方面具有显著有效性,但其准确性和性能高度依赖于其超参数。在采用试错法前提下,构建一个具有较高准确性和可靠性的合适ML模型需要花费大量精力和时间。
鉴于此,本文对橡胶改性再生骨料混凝土在不同温度作用下的单轴抗压强度(UCS)进行试验研究,引入了元启发式优化算法,利用萤火虫算法(FA)自动调整ML模型的超参数,以预测不同配合比和温度条件下混凝土的抗压强度,为其路用性能的定量评估提供依据。
2 材料和方法
2.1 原料和混合比例
采用粒径5 mm以内的连续级配中砂,细度模数为2.52,表观密度为2 679 kg/ m3。从深圳一座旧建筑中挤压出来的再生骨料通过替换等量的天然骨料被纳入RAC。采用颚式破碎机(PE900×1 200,中国)将废混凝土粉碎成合适粒度的小块。RA的主要成分是制造商检测的完整石头(35%)、二次骨料(57%)、砂浆块(7%)和杂质(1%)。此外,玻璃、木屑等杂质也被去除。由于RAs含泥量高,按照GB/T 25177[10]的要求,在饱和干燥条件下对RAs进行洗涤干燥。NA和RA的物理性质见表1。NA和RA的分级曲线如图1所示。RPs
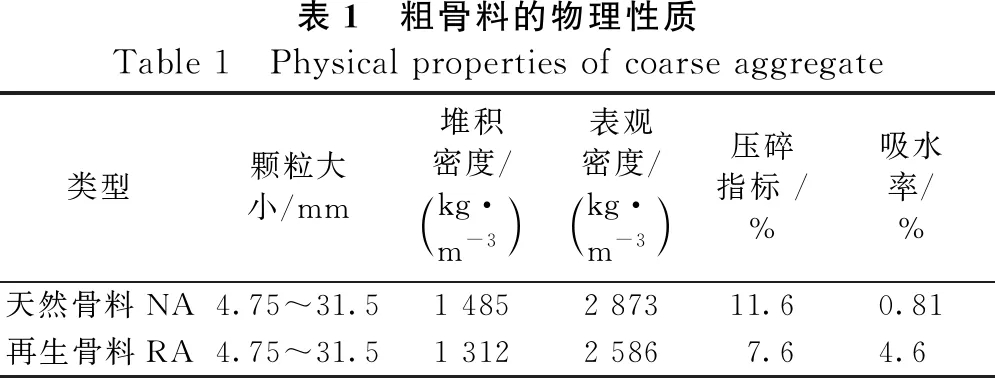
表1 粗骨料的物理性质Table 1 Physical properties of coarse aggregate类型颗粒大小/mm堆积密度/kg·m-3 表观密度/kg·m-3 压碎指标 /%吸水率/%天然骨料NA4.75~31.51 4852 87311.60.81再生骨料RA4.75~31.51 3122 5867.64.6
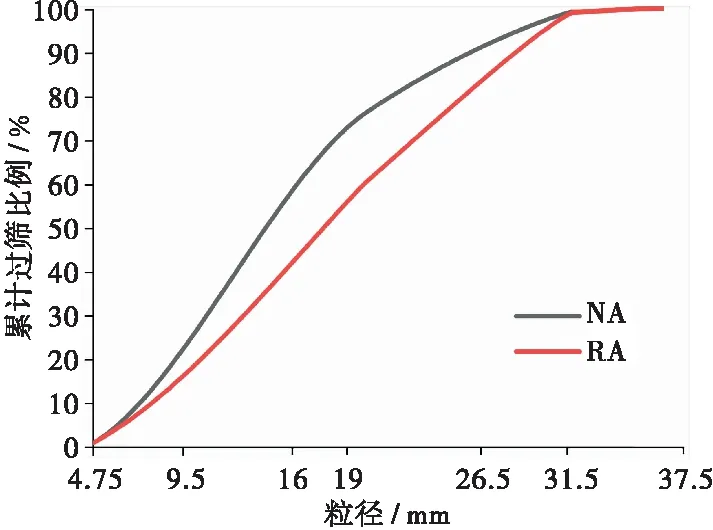
图1 NA、RA级配曲线
粒径约0.86 mm,表观密度约为1 020 kg/m3。
本试验拟采用RA体积替换0、25%、50%、75%、100%的NA,用RPs体积替换0%、5%、10%、15%的砂石。聚羧酸减水剂用量为4.1 kg/m3。水胶比保持在0.5。变量和机器学习模型输出目标的统计学参数如表2所示。根据试验所得数据制成数据库,通过建立UCS/峰值应变与混凝土配合比的关系来训练机器学习模型。
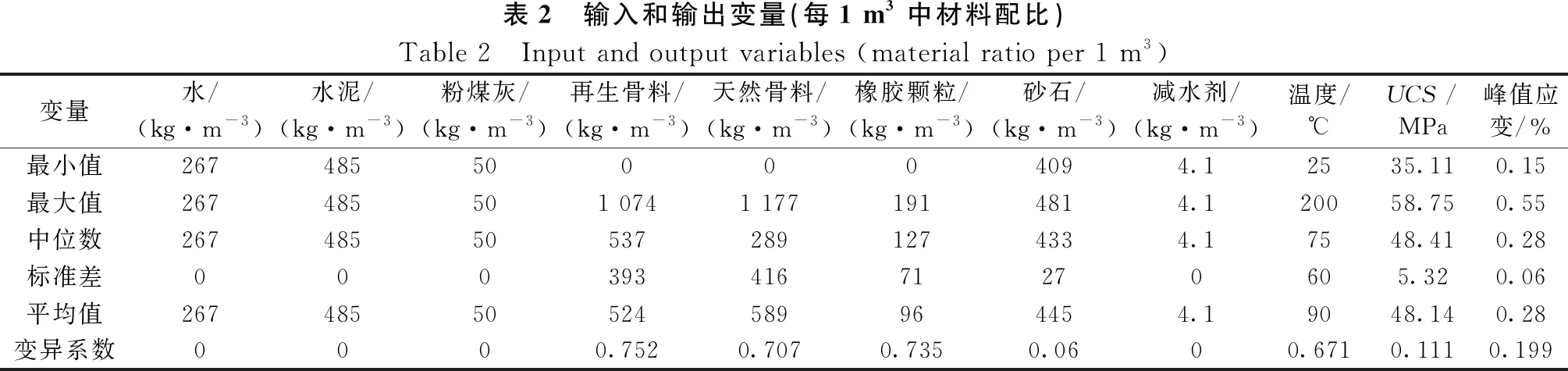
表2 输入和输出变量(每1 m3中材料配比)Table 2 Input and output variables (material ratio per 1 m3)变量水/(kg·m-3)水泥/(kg·m-3) 粉煤灰/(kg·m-3) 再生骨料/(kg·m-3) 天然骨料/(kg·m-3) 橡胶颗粒/(kg·m-3) 砂石/(kg·m-3) 减水剂/(kg·m-3) 温度/℃UCS/MPa峰值应变/%最小值267485500004094.12535.110.15最大值267485501 0741 1771914814.120058.750.55中位数267485505372891274334.17548.410.28标准差00039341671270605.320.06平均值26748550524589964454.19048.140.28变异系数0000.7520.7070.7350.0600.6710.1110.199
2.2 样品制备与测试
试样尺寸为Φ150 mm× 300 mm。浇筑试件24 h后从模具中取出试样并标准温度(20±2) ℃、相对湿度95%的条件下养护28 d。高温处理采用温度控制精度±1 ℃的SX2-28-13式箱式电炉,试样与炉壁之间的距离控制在20 mm以上,以确保试样表面均匀加热。加热速率设置为5 ℃/min。在达到目标温度(T,即50 ℃、75 ℃、100 ℃或200 ℃)后,温度保持恒定60 min,然后停止加热。取出标本,室温至冷却。
进行单轴压缩试验。压缩前,在每个圆柱体的两端表面覆盖一层石膏平整层。在4 000 kN万能试验机(Matest C088-01)上进行压缩试验。加载速率设定0.18 mm/min,使用2台线性变量差动变压器(LVDTs)测量气缸的纵向变形。此外,位移和力同步信号由应变采集装置(JM3841,晶明科技有限公司,中国)记录,采集频率为1 Hz。随后取各组3个试件的UCS和对应峰值应变平均值。
3 机器学习模型
本文采用了反向传播神经网络(BP)、随机森林(RF)、基准模型、作为机器学习模型,利用萤火虫算法(FA)调整机器学习模型的超参数。BP和RF的理论在此不做详述。基准模型本试验选择逻辑回归(logic regression, LR)和多元线性回归(multiple linear regression, MLR)作为基准模型,与RF和BP模型预测性能进行比较,为选择最佳模型提供判断依据。LR和MLR模型可以用以下公式表示:
(1)
Y=β0+β1x1+β1x2+…+βnxn
(2)
式中:xk为自变量;p为因变量b0和bk是常系数;Y是输出;xn是多个预测变量;β1,…,βn表示回归系数。
萤火虫算法的灵感来自于萤火虫的社会行为,该算法符合以下3条规则:① 不论性别,萤火虫都会因亮度差异而互相吸引。② 吸引力与萤火虫的亮度相对应,当两只萤火虫之间的距离增加时,亮度都会降低。如果没有比自己更亮的萤火虫,萤火虫就会在周围随意移动。③ 萤火虫的亮度是由一个特定问题的目标函数控制的。
根据式(3),一只萤火虫将飞向亮度更高的一只萤火虫:
(3)
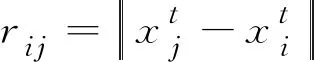

图2 萤火虫算法伪代码
本试验采用五折交叉验证,首先将数据集随机分为测试集和训练集,分别占数据集的30%和70%。其次,将训练集分为5份,其中4份用于训练RF模型,最后1份用于验证。ML模型的超参数在训练过程中通过FA算法在50次迭代过程中不断更新,并记录验证集上计算的均方根误差(RMSE)的最小值。该过程重复5次,完成5次交叉验证。最后,将最优超参数的ML模型用于整体样本数据的预测。
机器学习模型性能评价指标为均方根误差(RMSE)和相关系数(R),定义如下式所示:

(4)
(5)
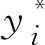
4 试验结果分析
根据100组单轴压缩试验结果,图3表示了抗压强度随橡胶掺量RPs、建筑固废掺量RA和温度的影响规律。总体而言,UCS与RA替换率呈负相关。当RPs掺量为10%,温度为25 ℃时,单轴抗压强度随RA掺量的增加而降低,降低幅度在10%以内。再生骨料混凝土的组成包括NA、RA中的旧砂浆、新砂浆和新旧砂浆之间的新界面过渡区(ITZ)[12]。由于RA具有较高的吸水率,在其表面形成一层水膜可以减少新的ITZ。因此,随着RA含量的增加,裂纹更有可能沿着减弱的过渡段发展,从而降低单轴抗压强度。此外,由于RPs的负面影响,室温下不含橡胶骨料的试样的单轴抗压强度普遍高于掺橡胶骨料的试样。
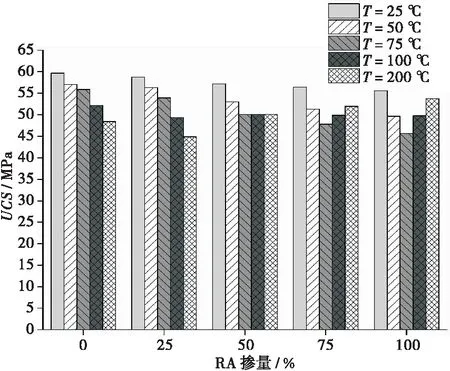
(a)RP掺量为0%
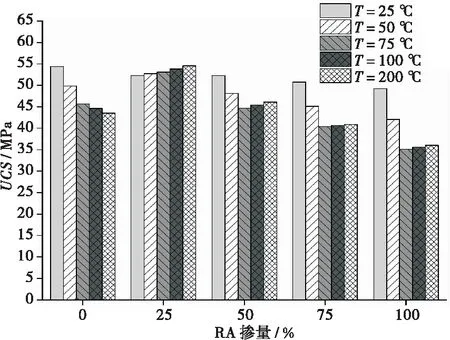
(c)RP掺量为10%
在高温的影响下,各配合比的RRAC的抗压强度均有明显降低。当温度从25 ℃增加到50 ℃、75 ℃、100 ℃、200 ℃时,掺有50%RA, 5% RPs的样品的抗压强度分别从53.03 MPa下降到50.00、47.91、47.87 、47.83 MPa。然而,在高温下,RA可以一定程度缓解抗压强度的下降。例如,200 ℃的环境下,25%和50% RA的RRAC比不掺入RA的混凝土具有更高的抗压强度。这一现象也与以往的研究结果一致[13-14]。这是因为与NA相比,RA孔隙率较高,内部微裂纹较多,可释放蒸汽压力。此外,RA的热膨胀系数更接近砂浆[14]。
5 机器学习预测结果
5.1 机器学习模型性能对比
图4所示为BP(反向传播神经网络)、RF(随机森林法)、LR(逻辑回归基准模型)和MLR(多元线性回归基准模型)的预测箱型图,其中BP和RF中引入基于萤火虫算法进行超参数调整。
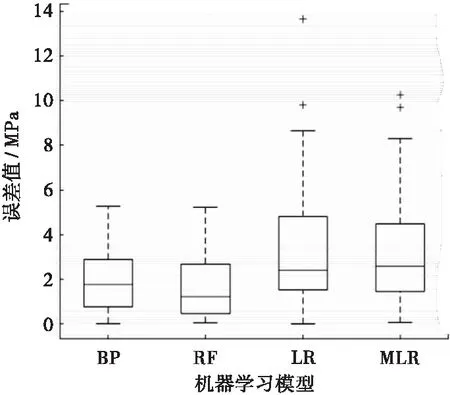
图4 各模型抗压强度预测箱型图
图4中的方框表示每个模型的四分位数范围。由图可知,RF的上下边界高度最小且中值(框内红线)最低,预测误差最小。RF在预测峰值应变时存在2个异常值,但整体而言,在UCS和应变的预测中,RF的误差上限均低于BP、LR和MLR,表明在这些ML模型中,RF模型的准确度最高。图5为预测泰勒图,表征了R、RMSE和标准差3个指标。在UCS预测中,RF最接近“实际”点,相关系数最高,RMSE最低,标准差最低。表3列出了UCS预测的具体RMSE和R值。综上,在4种ML模型中,RF模型的性能最好。
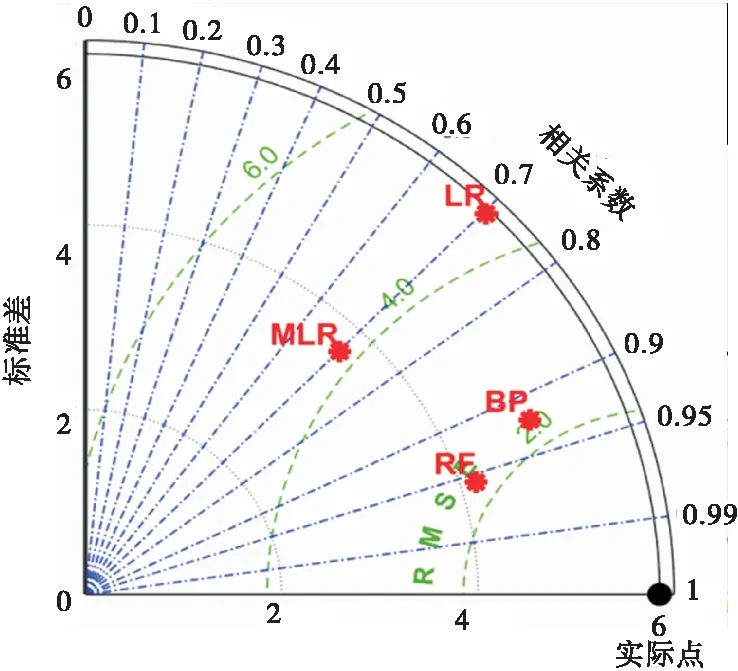
图5 各模型抗压强预测泰勒图
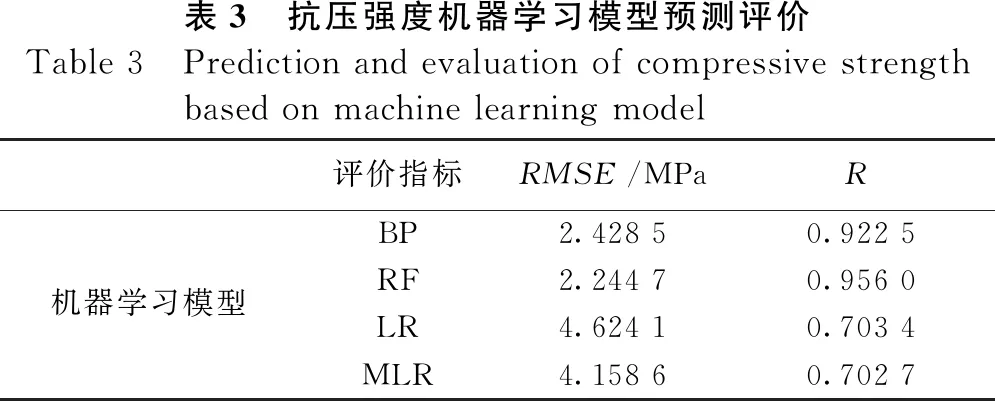
表3 抗压强度机器学习模型预测评价Table 3 Prediction and evaluation of compressive strength based on machine learning model评价指标RMSE/MPaRBP2.428 50.922 5机器学习模型RF2.244 70.956 0LR4.624 10.703 4MLR4.158 60.702 7
5.2 RF的超参数优化
由于RF模型的预测性能最好,本节将对RF的超参数调优和性能分析进行描述。萤火虫算法(FA)的超参数为决策树个数和最小叶子节点样本数,试验采用五折交叉验证和FA算法在50此迭代中更新超参数,以获得使验证集RMSE最小的超参数组合。图6显示了RF模型的超参数调优过程,其中图6(a)显示了5次交叉验证中各验证集上的RMSE最小值,图6(b)显示了RMSE随迭代次数不断减小的过程。针对UCS数据集,FA算法推荐23棵树,每棵树叶子节点的样本数为1;针对峰值应变数据集,FA算法推荐45棵树,每棵树叶子节点的样本数为1。
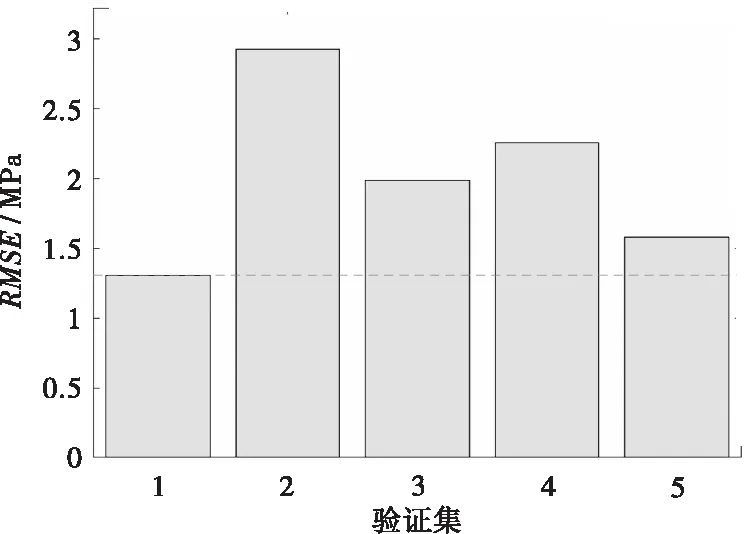
(a) 5个UCS验证集的RSME最小值
5.3 FA-RF模型的预测性能
图7(a)和(b)描述了在70%UCS训练集和30%测试集上FA-RF模型的预测值和误差,抗压强度的误差不超过4 MPa。图8直观体现了模型预测值偏离实测值(对角线)的程度。FA-RF 在UCS训练集和测试集的预测相关系数分别为0.967 7和0.956 0,RMSE分别为1.491 8和2.244 7 MPa。FA-RF模型在预测单轴抗压强度时,对于训练集和测试集,都具有较高的相关系数和较低的RMSE值,因此具有良好的预测性能。
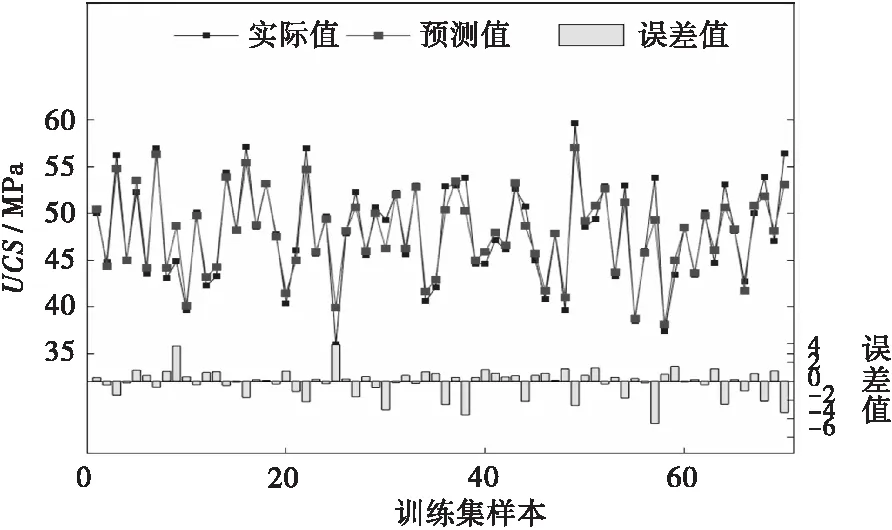
(a) 训练集
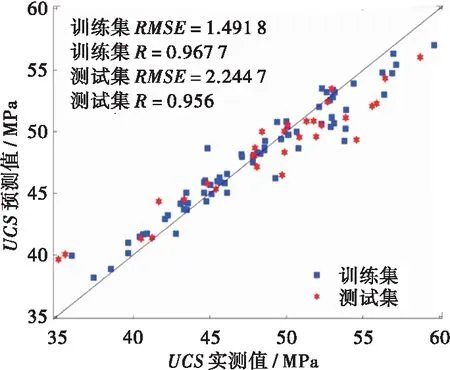
图8 抗压强度预测散点图
6 结论
本文研究了建筑固废、废弃橡胶和温度对单轴抗压强度的影响,对橡胶改性再生骨料混凝土的路用性能预测提供评价依据。在试验结果的基础上,应用机器学习模型预测UCS,主要结论如下:
a.室温下RA掺量、RPs掺量和温度均与UCS呈负相关。而RA能够降低高温处理后的强度损失。此外,由于橡胶熔体更有效地释放了蒸汽压,则RPs降低了高温下UCS的损失。
b.从箱型图和泰勒图可以看出,与其他3种机器学习模型(BP、LR和MLR)相比,RF模型的R值最高,RMSE值最低,说明其具有最好的预测性能。
c.加入萤火虫算法进行超参数调整后,FA-RF在UCS训练集和测试集的预测相关系数分别为0.967 7和0.956 0,RMSE分别为1.491 8 MPa和2.244 7 MPa,适用于橡胶改性再生骨料混凝土的强度预测,为根据工程需求配置再生骨料混凝土提供了可靠依据。
