基于子集模拟的预制构件生产目标均衡优化算法研究
2022-12-04金艳琪陈雅含
王 家,金艳琪,陈雅含
(湖南大学 土木工程学院,湖南 长沙 410082)
0 引言
预制构件生产是装配式建造推广的重要环节之一,在预制构件生产过程中,涉及到人力、材料、机械等多方面。随着我国建造领域工业化的不断推进[1],对预制构件的需求量不断增长,对预制构件的质量要求也不断上升[2]。而目前我国预制构件生产加工厂普遍存在技术管理人员专业化技术和产业化实施能力不足的问题[3],这一现状使得预制构件呈现出总体生产成本较高,总体环境效益不显著的弊端。预制构件生产目标均衡的目的在于为预制构件的生产工序选择合适的生产执行模式组合,科学合理地根据构件生产需求制定生产方案,提高预制构件生产效率,降低预制构件生产成本,增强预制构件的环境效益,从而促进装配式建筑行业的高质量发展。
预制构件生产过程中的目标均衡优化问题有着复杂的含义。从目标考虑,可以分为成本优化问题[4-5]、效率优化问题[6-7]、碳排放优化问题[8-9]和库存优化问题[10]等,以及不同类型优化目标的组合优化问题。从算法考虑,可以分为精确算法求解问题和启发式算法求解问题。精确算法主要基于动态规划、整数规划、分支界定等方法[11],而启发式算法主要基于遗传算法[12-13]、蚁群算法[14]、粒子群算法[15-16]、共生生物搜索算法[17]等算法。预制构件生产目标均衡问题的复杂程度随着工序数量的增加而急剧上升,因此,针对工序数量较多的预制构件生产目标均衡问题,精确算法并不适用,只能采用启发式算法。但是,现有启发式算法具有随机性,在最优解获取稳定性上仍有较大的改进空间。
为此,本文针对预制构件生产目标均衡优化问题,提出一种基于子集模拟的启发式优化算法。利用聚集函数法,将生产时间、成本和生产过程中产生的碳排放纳入优化目标,构建多模式下预制构件生产目标均衡优化模型。同时为了增强子集模拟在全局范围的搜索能力,采取均匀间隔取点的马尔科夫链方法,增加样本点的多样性。通过实际案例的验证,与改进的遗传算法相比,本文提出的优化算法在最优解获取的稳定性上有较好改进。
1 预制构件生产目标均衡优化模型
考虑包含n道工序,每道工序i(i=1,2,…,n)涉及mi种生产执行模式的预制构件生产项目。该项目中第i道工序的第j(i=1,2,…,mi)种执行模式的持续时间、耗费成本和产生的碳排放分别表示为tij,cij和eij。预制构件生产目标均衡优化模型中,一般通过指示变量Xij表示工序i所选择的执行模式,如工序i选择第j种执行模式,则Xij=1。因各工序仅能选择一种执行模式,指示变量需满足如下约束条件:
(1)
项目的调度方案,可表示为包含所有指示变量的矩阵X={Xij,i=1,…,n,j=1,mi}。例如,表1为某生产项目目标均衡方案的矩阵表示,该项目包含5道工序,每道工序对应的执行模式总数分别为4、2、4、4和3。由指示变量Xij的含义可知,该项目调度方案中,工序1~5所选择的执行模式分别为第2、第1、第3、第3和第2。
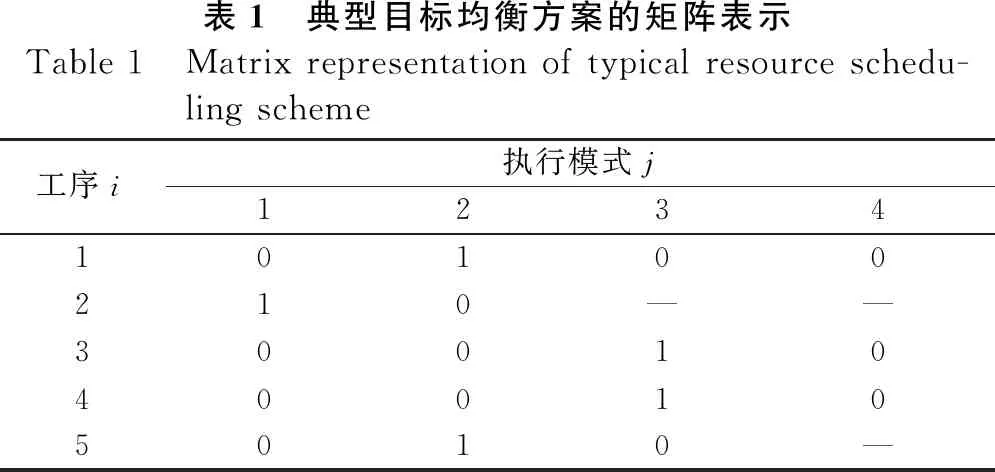
表1 典型目标均衡方案的矩阵表示Table 1 Matrix representation of typical resource schedu-ling scheme工序i执行模式j123410100210——30010400105010—
在给定项目调度方案X={Xij,i=1,…,n,j=1,mi}下,生产项目的工期T(X)可通过调度方案X中各工序执行模式的生产时间累加得出,如式(2)所示:
(2)
式中:L表示关键路径上工序的集合。同理,可以求出生产项目的总制造成本C(X)和总碳排放量E(X):
(3)
(4)
预制构件生产均衡优化的目标, 是通过对工序执行模式的合理组合,尽可能实现项目工期、成本和碳排放量的最小化.为综合考虑工期、成本和碳排放量3项子目标,本文将各子目标无量纲化,并分配反映重要性程度的权重系数,进而建立如下的优化模型:
(5)
s.t.
T(X)≤T*,C(X)≤C*,E(X)≤E*
其中,Tmin,Cmin,Emin为各子目标的下限值;Tmax,Cmax,Emax为各子目标的上限值;w1,w2,w3为各子目标在模型中的权重系数;本文采用层次分析法确定,T″,C″,E″分别为各子目标的最大容许值。
生产项目的调度方案,也可采用向量的表示形式θ=(θ1,θ2,…,θn)。此时,向量θ中的元素θi,i=1,…,n代表工序i的执行模式,为[1,mi]内的自然数。由项目调度方案的矩阵表示X与向量表示θ的含义可知,X与θ间存在一一对应关系.例如,表1的矩阵表示X,对应工序1~5分别选择第2、第1、第3、第3和第2执行模式的调度方案, 其向量表示为θ=(2,1,3,3,2)。利用X与θ间的一一对应关系X=X(θ),可得调度方案向量表示下的优化模型:
(6)
s.t.
T(θ)≤T*,C(θ)≤C*,E(θ)≤E*
式(4)的优化模型为离散型优化模型,某些情形下针对其等价的连续性优化模型进行求解更为方便.式(4)的优化模型中,决策变量θi,i=1,…,n为[1,mi]内的自然数, 可针对其引入(0,1]间取值的连续性决策变量ui,i=1,…,n, 并建立两者间的函数关系如下:
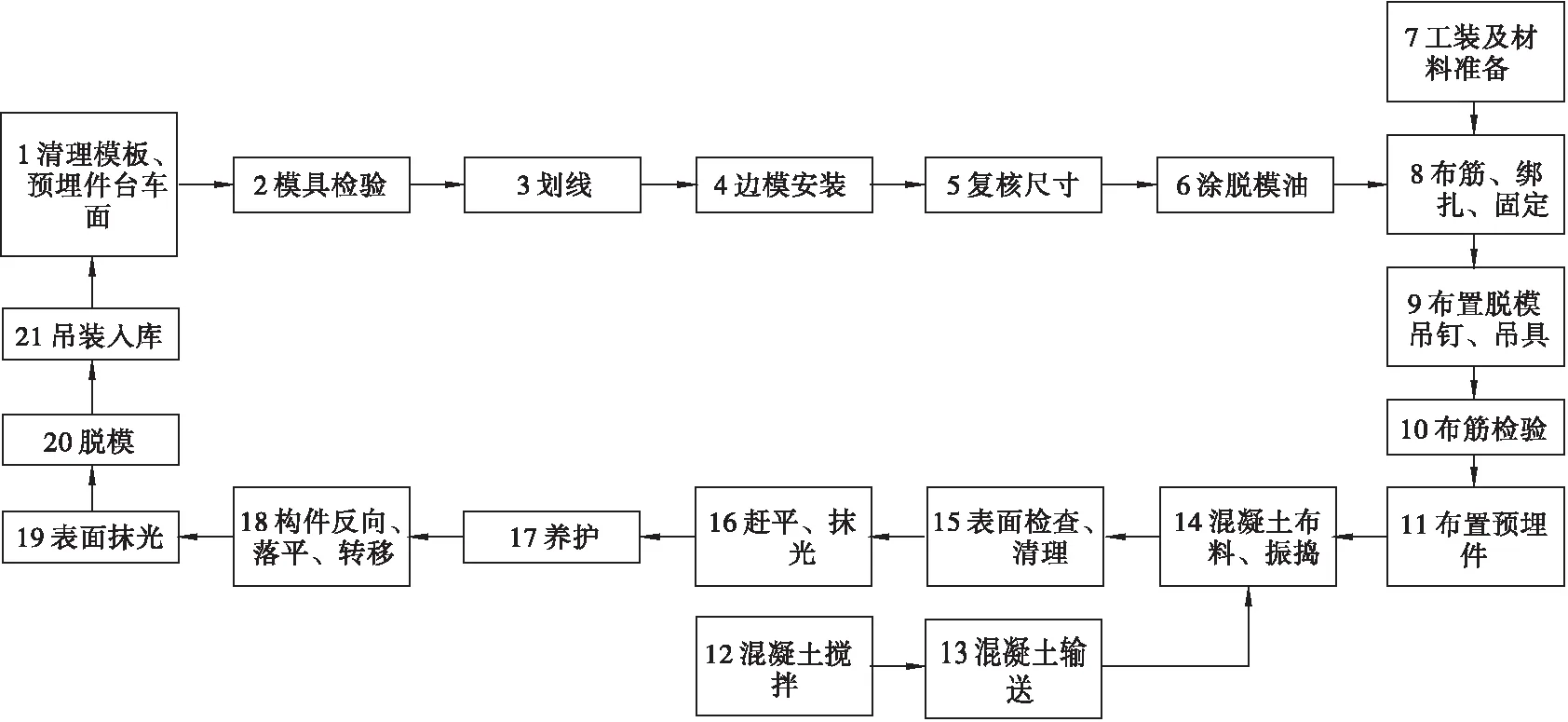
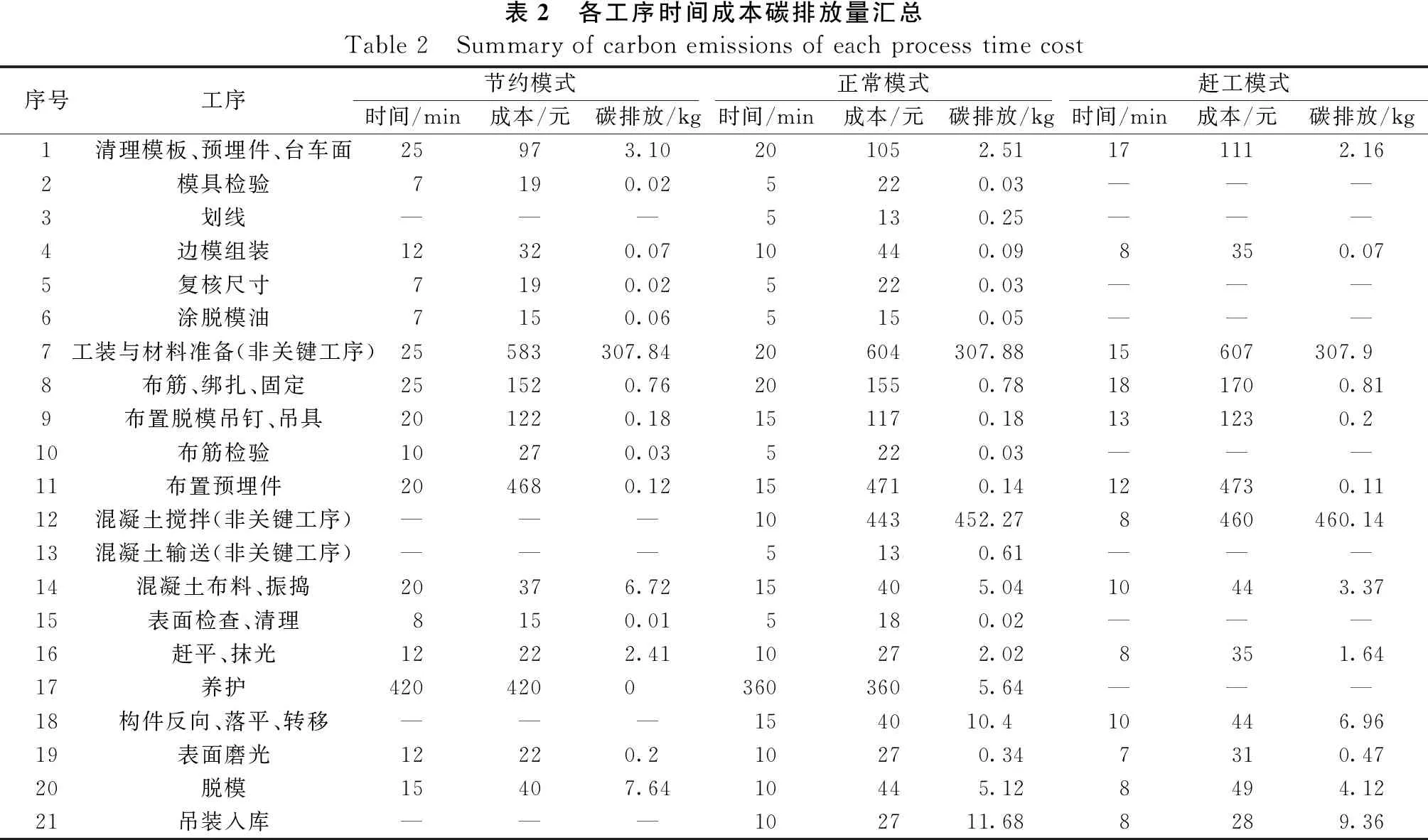
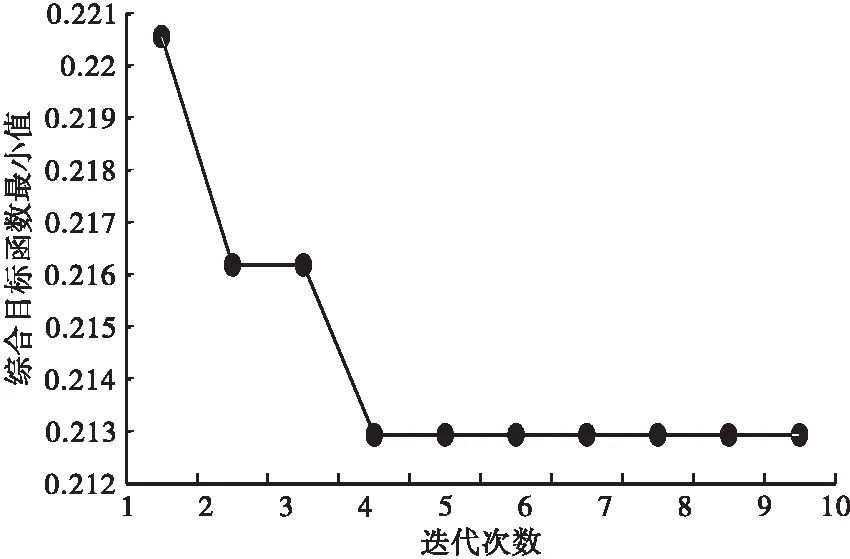
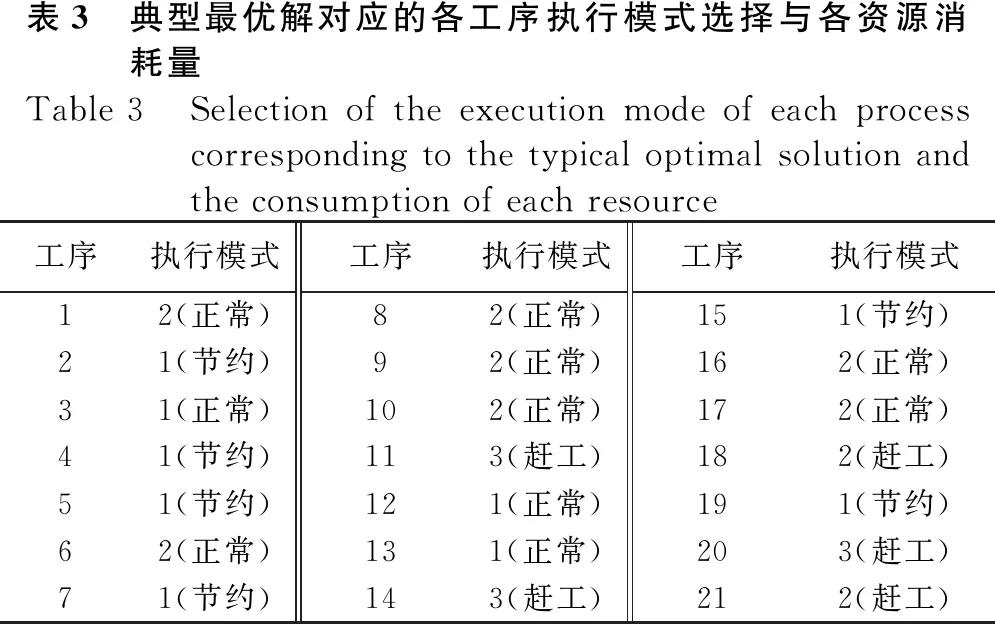
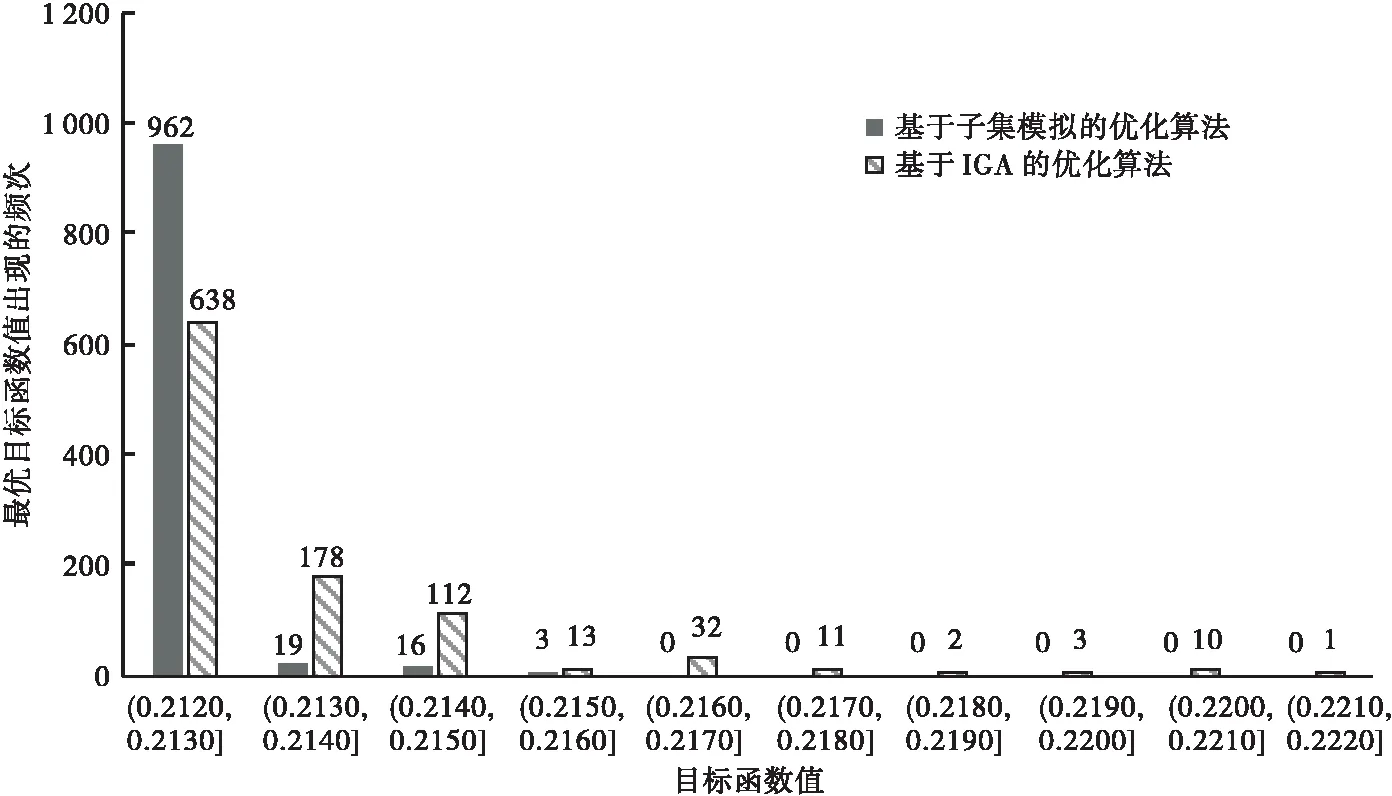
θi=ceil(ui×mi),0 (7) 式中:函数ceil()为向右取整函数。此时,预制构件生产调度优化模型可以表示为连续型决策变量U=(u1,u2,…,un)下的优化模型: (8) s.t. T(θ(U))≤T*,C(θ(U))≤C*,E(θ(U))≤E*0 子集模拟法(Subset Simulation)是 Au 和 Beck 提出的,针对结构可靠度问题的高效数值模拟算法[18]。其思想是通过引入一系列中间失效事件,将偶发事件的小概率表示为一系列较大的条件概率乘积, 进而将小概率估计问题转化为一组较大的条件概率的估计问题[19],以提高数值模拟算法的计算效率。通过利用可靠度问题和优化问题的内在联系,子集模拟方法在优化设计问题中也取得了较好的应用[20]。 考虑如下优化问题: minf(U) (9) s.t. 0 T(U)≤T*,C(U)≤C*,E(U)≤E* 为利用子集模拟法求解上述优化问题,人为设定变量U为随机变量,服从可行域Ω0={U∶0 a.在区域Ω={U∶0 考虑到预制构件生产优化问题中变量U的维数(对应项目中的工序数量)较大,本文采用改进Metropolis-Hasting方法[17],以完成上述马尔科夫链中的迭代操作。具体而言,方法采用一维均匀分布的概率密度分布函数p*(ξ/u)作为建议概率密度分布函数。该函数以u为中心,以d为宽度(即u-d/2≤ξ≤u+d/2)(d一般取0.2~0.4),可自动满足对称性的要求。马尔可夫链中Uk=(uk,1,uk,2,…,uk,n)到Uk+1=(uk+1,1,uk+1,2,…,uk+1,n)的迭代操作如下: 如2.1节所述,基于子集模拟的优化算法中,需根据在收缩区域Ωj内的少量样本点,利用MCMCS方法产生要求数量的样本点。方法中具体的马尔科夫链迭代操作与2.2节类似,但需额外考虑收缩区域的边界限制f(U)≤fj,因此,需将2.2节马尔科夫链迭代操作中的步骤修改如下: 在实际运算过程中,为了避免MCMCS产生的样本点陷入局部最优,采用均匀间隔取点的方式,每间隔e个状态点选择一点作为样本点。如图1所示。以p0=0.1,M=100,e=3为例,当Uk作为一条链条的起点时,如果采取连续取点的方法,那么需要通过MCMCS方法产生(1/p0-1)=9个状态点,这些点全部作为样本点。此时,马尔科夫链长度为10。如果间隔取点,则需要产生[1/p0×(e+1)-1]=39个状态点,此时,马尔科夫链长度为40。取第5,9,13,…,37个点作为样本点。通过间隔取点的方法,产生的样本点更具有多样性。 (a) 连续取点的马尔科夫链 针对以上预制构件生产目标均衡优化模型,本文基于子集模拟法,建议的优化算法步骤总结如下:a.确定子集模拟算法中的参数,即在指定区域中抽样的样本数量M、条件概率参数p0、改进Metropolis-Hasting方法中定义一维均匀概率分布的宽度d和MCMCS中均匀间隔取点数e。 e.算法采用的迭代终止原则为达到预先设定的迭代次数J。如不满足迭代终止条件,即j>J,令j=j+1,重复步骤4。 以文献[21]中某预制构件厂一预制构件生产线为例,该生产线包含21道生产工序,如图2所示。每道工序对应节约、正常、赶工3种执行模式,每种执行模式下对应的生产时间、花费成本和产生的碳排放量如表2所示。受到外界资源限制,最大生产时间阈值T*=540 min,最高生产成本阈值C*=2 600元,最大生产碳排放阈值E*=800 kg(碳排放指二氧化碳当量,全文同)。 图2 某预制构件生产流程图 需要注意的是,工序7、12、13为非关键工序,不计入生产总时间。根据表2,可以计算出仅考虑单个资源消耗的理想值Tmax=640 min,Cmax=2 769元,Emax=818.37 kg;Tmax=509 min,Cmax=2 556元,Emax=790.03 kg。利用层次分析法,通过专家打分,各资源的相对权重确定为[w1,w2,w3]=[0.2,0.2,0.6]。 表2 各工序时间成本碳排放量汇总Table 2 Summary of carbon emissions of each process time cost序号工序节约模式正常模式赶工模式时间/min成本/元碳排放/kg时间/min成本/元碳排放/kg时间/min成本/元碳排放/kg1清理模板、预埋件、台车面25973.10201052.51171112.162模具检验7190.025220.03———3划线———5130.25———4边模组装12320.0710440.098350.075复核尺寸7190.025220.03———6涂脱模油7150.065150.05———7工装与材料准备(非关键工序)25583307.8420604307.8815607307.98布筋、绑扎、固定251520.76201550.78181700.819布置脱模吊钉、吊具201220.18151170.18131230.210布筋检验10270.035220.03———11布置预埋件204680.12154710.14124730.1112混凝土搅拌(非关键工序)———10443452.278460460.1413混凝土输送(非关键工序)———5130.61———14混凝土布料、振捣20376.7215405.0410443.3715表面检查、清理8150.015180.02———16赶平、抹光12222.4110272.028351.6417养护42042003603605.64———18构件反向、落平、转移———154010.410446.9619表面磨光12220.210270.347310.4720脱模15407.6410445.128494.1221吊装入库———102711.688289.36 为检验基于子集模拟的目标均衡优化算法的性能,每代随机抽样样本取M=1 000,条件概率参数取p0=0.1,筛选产生初始样本点数量取t=10,改进Metropolis-Hasting方法中一维均匀概率分布的宽度取d=0.30,MCMCS中均匀间隔取点数取e=3。图3描述了基于子集模拟的建议优化算法一次典型求解过程中,最优目标函数值随迭代阶段的变化。由图3可知,算法经过4次迭代后收敛到最优解,对应最优目标函数值0.212 9。该最优解对应的各工序执行模式的选择如表3所示,对应生产时间T=534 min,花费成本元C=2 598元,产生的碳排放量E=796.42 kg。 图3 建议优化算法典型求解过程中最优目标函数值随迭代阶段的变化 为检验基于子集模拟的建议优化算法的稳定性,设计了改进的遗传算法( Improved Genetic Algorithm,IGA)进行对比。经过试验,传统的GA无法在相对有限的时间内,随机产生足够数量满足约束条件的初始样本点。因此,运用2.2节中的方法对初始种群的产生方法进行处理,得到改进后的遗传算法(IGA)。考虑到交叉概率参数pc和变异概率参数pc对 IGA 算法求解的影响,本文进行了大量pc和pm组合取值,检验发现,交叉概率pc=0.9和变异概率pm=0.05下,IGA 算法求解本案例目标均衡问题的性能最优,因此表4给出的是这组交叉概率和变异概率下IGA 算法的对比结果。同时,考虑到计算资源对2种优化算法的影响,结合两种算法的特点,在子集模拟算法中,每代样本点取1 000,迭代终止条件为最优解连续3次迭代保持不变,再将子集模拟实际的运算量作为IGA的迭代终止条件。 表3 典型最优解对应的各工序执行模式选择与各资源消耗量Table 3 Selection of the execution mode of each process corresponding to the typical optimal solution and the consumption of each resource工序执行模式工序执行模式工序执行模式12(正常)82(正常)151(节约)21(节约)92(正常)162(正常)31(正常)102(正常)172(正常)41(节约)113(赶工)182(赶工)51(节约)121(正常)191(节约)62(正常)131(正常)203(赶工)71(节约)143(赶工)212(赶工) 表4提供了2种算法1 000次独立运行求解获得的最优目标函数值的统计结果(最小值、平均值、最大值和标准差)。对比可知,基于子集模拟的优化算法获得最优目标函数值的平均值为0.213 0,小于基于 IGA 的优化算法的相应数值(0.213 5),且最优目标函数值的标准差值更小。此外,图4给出了2种算法 1 000 次独立运行获得的最优目标函数值的分布情况。由图4可见,基于子集模拟的优化算法性能更优,其获得的最优目标函数值分布更为集中,有96.2%的最优目标函数值集中在(0.212 0,0.213 0]区间,表明基于子集模拟的建议优化算法获取最优解的稳定性更高。 表4 基于子集模拟的优化算法与 IGA 算法独立运行 1 000 次获得的最优目标函数值的统计结果Table 4 The statistical results of the optimal objective function value obtained by the optimization algorithm based on the subset simulation and the IGA algorithm independently run 1 000 times算法最优解的目标函数值统计最小值平均值最大值标准差基于子集模拟的优化算法0.212 90.213 00.215 82.682 7E-04基于IGA的优化算法0.212 90.213 50.225 20.001 3 图4 两种优化算法独立运行 1 000 次获得的最优目标函数值的分布 本文针对预制构件生产项目的目标均衡优化问题,基于子集模拟法进行启发式优化算法的研究,主要研究结论如下: a.在构建预制构件生产目标均衡优化模型时,引入权重系数,对多个优化目标进行处理,并通过映射条件,将离散型变量问题转化为连续型变量求解问题。 b.针对预制构件生产目标均衡优化模型,提出基于子集模拟的建议优化算法,并给出算法框架和具体操作步骤。 c.为产生满足约束条件的初始种群,采用随机产生和MCMCS相结合的方法,先筛选少量满足约束的初始样本点,再以MCMCS的方法扩充至整个初始种群,提高计算效率。 d.为避免收缩区域内样本点产生陷入局部最优,采取均匀间隔取点的马尔科夫链方法,增强子集模拟在全局范围的搜索能力,丰富种群的多样性。 e.通过算例验证,与改进的遗传算法相比,基于子集模拟的建议优化算法在最优解的获取稳定性上有较大改进。2 基于子集模拟的生产调度优化算法
2.1 基于子集模拟的生产目标均衡优化算法框架
2.2 可行域Ω0内均匀分布样本点的产生
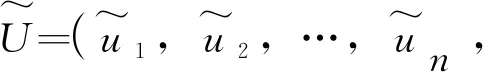
2.3 收缩区域Ωj={U∶U∈Ω0,f(U)≤fj}内均匀分布样本点的产生
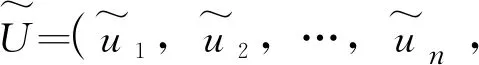
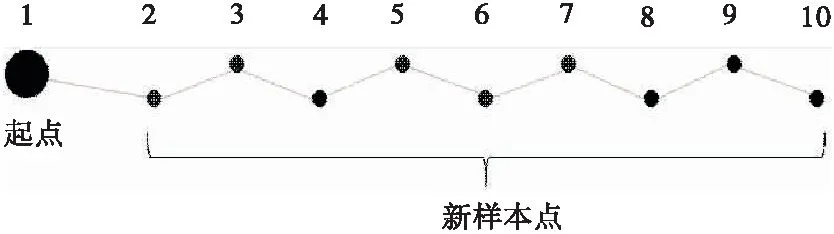
2.4 基于子集模拟的预制构件生产目标均衡优化算法总结
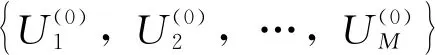
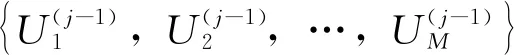
3 案例分析

4 结论
